考虑数值积分算法的实时子结构试验稳定性研究

2021-11-17 07:43鲁旭杰周子豪李忠献

工程力学 2021年11期

李宁，鲁旭杰，周子豪，李忠献

(1. 天津大学建筑工程学院，天津 300350；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300350；3. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学)，天津 300350)

近年来，随着隔震、减震/振结构中，采用动力特性与变形速率相关的新装置大量涌现，传统拟/静力试验方法无法适应测试和研究需要，快速或实时混合模拟(real-time hybrid simulation，RTHS)方法[1-2]正推广用于结构动力性能研究。RTHS试验常将原结构划分为2 部分，其中本构关系复杂、无法准确建立模型或使用数值模拟的结果不理想的部分一般作为物理子结构，用作动器或振动台等加载装置进行加载；其余模拟方法成熟、较为准确的部分作为数值子结构，使用模拟软件模拟。两部分之间进行同步或高速数据交互。当反馈与命令达到实时交互时，也称为实时子结构试验(real-time substructure test，RTST)。

以图 1 所示单层框架为例，RTST 在试验开始时，首先输入地震动，由数值子结构计算出命令位移，作动器或振动台根据命令施加动边界给物理子结构，再通过物理子结构上的传感器测得其反应，通过DAQ 将反应量传输给数值子结构，两者进行数据交互。如此循环往复，直至试验结束。

图1 实时混合模拟试验Fig. 1 Real time hybrid simulation

近两年，国内外学者通过实时混合试验对多种结构的特性进行了试验研究。例如，李腾飞等[3]通过基于OpenFresco 试验平台的混合试验系统对高强钢组合K 形偏心支撑钢框架的抗震性能进行了研究；Mukai 等[4]应用实时混合试验技术通过双作动器对混凝土框架结构在主动调谐质量阻尼器控制下的结构性能进行了研究。Najafi 等[5]用实时混合试验对配有非线性能量阱结构的动力特性进行了研究。

RTST 目前的研究热点有：时滞补偿、复杂边界或加载方法，以及稳定性分析等。RTST 成功与否的关键是保证系统的稳定[6]。在RTST 中，由于数值子结构的求解属于离散时间系统，物理子结构的响应以及作动器或振动台等加载元件的运动是连续时间系统，RTST 应属于连续-离散混合系统。对此，建立对应的分析模型和理论还是国内外热点问题之一。目前主要采用连续时间系统或离散时间系统两类方法对RTST 进行稳定性探究。

采用连续系统模型，Wallace 等[7]使用时滞微分方程导出了单自由度系统临界时滞表达式，给出其精确解。Kyrychko 等[8]将单自由度系统临界时滞计算方法推广到了多自由度系统。为了全面考虑结构划分对RTST 的影响，Maghareh 等[9]采用欧拉变换将时滞微分方程化简，得到不同结构划分方式(不同质量比、刚度比、阻尼)对系统稳定性的影响规律，认为结构划分在设计RTST 时必须考虑。

在RTST 中数值子结构需采用积分算法逐步求解，应考虑积分步长和积分算法假定对RTST稳定性的影响。许多学者对此问题进行了研究，例如：基于离散系统模型，Chen 等[10]结合作动器时滞假设和离散系统控制原理，得到了考虑数值积分算法后的系统稳定边界；王倩颖等[11]使用谱半径法研究了使用Operator-Split 积分算法的RTST试验稳定性随结构参数的变化；邓丽霞等[12]引入速度和加速度的附加假定，认为稳定性必须考虑试验和物理子结构质量之比的影响；Zhu 等[13]使用离散根轨迹方法研究了不同数值积分算法对多自由度RTST 系统时滞稳定性影响，认为时滞假设在低频时对加载系统的动力特性描述更精确；唐贞云等[14]通过对电液伺服加载系统进行建模，讨论了试件与加载系统对RTST 稳定性的影响；郭珺等[15]结合振型叠加法和增益裕度，认为时滞补偿对RTST 系统稳定性的影响不能确定。但是，既有的离散稳定性分析方法也存在一些不足，例如：Chen 等[10]提出的离散方法引用的时滞模型使其只适用于线弹性刚度和小时滞的情况；Zhu 等[13]提出的离散方法需要将要研究模型划分比例写成系统传递函数增益的形式进而通过根轨迹方法进行稳定性分析，使其局限为只能对质量划分比例进行研究的方法。这也表明离散系统稳定性分析方法的探索有待深入，也需要一种较通用的分析方法。

本文基于离散控制理论[16]，建立了引入积分算法的RTST 时滞系统传递函数，进而对系统传递函数的极点分布和系统的稳定性进行分析。在此基础上：一方面对RTST 中数值和物理子结构划分导致的系统稳定性的变化规律进行了详细的讨论，给出了其稳定区域以及对应的临界时滞，为RTST 中数值和物理子结构的划分及时滞补偿的可行性提供了依据；另一方面，本文也使用了其他两种连续系统假定的稳定性分析方法与本文所提方法得到的稳定性分析结果进行了对比，说明了本文方法更为安全可靠。

1 稳定性分析理论概要

1.1 稳定性分析概要

实时子结构系统可表述为一个闭环系统，如图 2 所示。

图2 实时子结构闭环控制系统的框图Fig. 2 Block diagram representation of real-time hybrid testing of an SDOF system

闭环控制系统的性能是由闭环传递函数Gcl(z)决定的：

1.2 引入数值积分算法的稳定性分析方法

使用基于极点分布的稳定性分析方法对SDOF的RTST 稳定性进行分析，其运动方程如下：

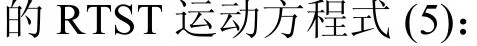
表1 传递函数系数Table 1 Transfer function coefficients

1.3 基于连续时间假设的临界时滞精确解

式中：j=1, 2, ···；k=0, 1, 2, ···。式(14)中正的临界时滞解才具有物理意义，且最小的正数解对RTST系统的稳定性最为关键，因为其代表了RTST 系统初次从稳定状态进入到不稳定状态。

1.4 基于连续时间假设的临界时滞近似解

2 考虑积分算法的RTST 稳定性分析

当系统时滞为0 时，RTST 的传递函数的稳定性由积分算法自身的稳定性控制(CR 积分算法此时无条件稳定)。当时滞不为0 时，考虑到RTST中时滞的真实情况，本文研究的时滞范围为0 s～1 s，并将结构在时滞范围为0 s～1 s 内都稳定的现象定义为“无条件稳定”。

某 SDOF 的质量M=52.56 kg，刚度K=87 600 N/m，阻尼比ζ=0.03，物理子结构的加载步长与数值子结构的积分步长都为0.01 s。本节研究物理子结构与数值子结构的质量比、刚度比，以及物理子结构与原结构的阻尼比作为自变量时，子结构划分对RTST 系统稳定性的影响。

2.1 质量之比作为自变量的稳定性探究

当以物理子结构、数值子结构的质量比作为变量时，令物理子结构的刚度及阻尼为0，此时其结构简图如图3(a)所示，使用劳斯-赫尔维茨稳定性判据可得该系统近似临界时滞的表达式为：

式(18)始终为负，故对于该工况，近似方法失效。该工况下的时滞稳定域图像如图3(b)所示。

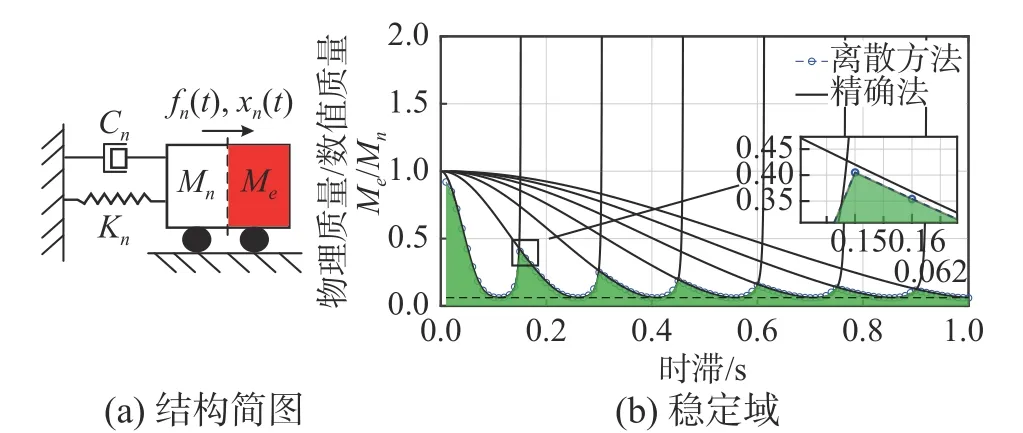
图3 实时子结构的时滞稳定域(Ke=0，Ce=0)Fig. 3 Delay stability region of RTST (Ke=0, Ce=0)

图 3(b)中绿色区域代表通过离散方法得到的稳定域，其他区域代表系统不稳定。可以看出，当质量比小于0.062 时，系统为无条件稳定，不受时滞条件影响。随着物理、数值子结构的质量比Me/Mn增加，该系统的稳定性显著下降，且当0.062＜Me/Mn＜0.427 时，系统出现稳定性切换现象，即随着时滞增加，系统在稳定状态与不稳定状态之间变换。精确方法绘制出的临界时滞曲线的上界全部收敛至Me/Mn=1 处，且稳定区域的上界也为1，说明了该工况下当且仅当Mn＞Me时，系统才可能稳定，反之，系统始终失稳。

虽然精确方法和离散方法总体上得到的稳定区域基本一致，但由局部放大图可以看出，离散方法得到的稳定域更小，说明了离散方法较精确方法更保守、接近实际。

2.2 刚度之比作为自变量的稳定性探究

当以物理、数值子结构的刚度比作为变量时，研究了如下4 种工况：1)Me=0；2)Me/Mn=0.5 ；3)Me/Mn=1 ；4)Me/Mn=2。图 4(a)为工况1 所对应的结构简图，图 4(b)为该工况的时滞稳定域。

如图 4 所示，随着物理、数值子结构的刚度比Ke/Kn增加，该系统的稳定域越来越小，稳定性越来越差，说明物理刚度的引入会降低RTST稳定性，而当Ke/Kn＜0.062时，该系统为无条件稳定，当 0.062 ＜Ke/Kn＜0.625时，该系统同样会出现稳定性切换现象。当Ke/Kn=1.5时，只要时滞足够小，通过连续方法也可绘制出临界时滞曲线，证明此时系统也是稳定的。说明了刚度比并不存在绝对的稳定上界。这一点与质量比显然不同。当时滞远小于1 ms 时，近似方法与精确方法绘制出的临界时滞边界十分接近；时滞较大时，近似方法绘制的临界时滞边界会迅速衰减，说明近似方法仅适用于小时滞情况；当时滞较大时，近似方法无法准确判断稳定性。此外，相对于连续时间系统稳定性分析方法，离散方法更加保守安全。

图4 实时子结构的时滞稳定域(Me=0，Ce=0)Fig. 4 Delay stability region of RTST (Me=0, Ce=0)

图5 分别为工况2～工况4 对应的稳定域图像。对比三幅图所绘制出稳定区域的大小可以看出，Me/Mn=0.5 时稳定域最大，Me/Mn=1得到的稳定域要小于Me/Mn=0.5时的稳定域，而当Me/Mn=2时，系统为无条件不稳定。一方面，证明了前述得到的“RTST 要保持稳定必须要满足质量比小于1”的结论(Me/Mn＜1)；另一方面，也说明物理子结构比重的增加会破坏RTST系统的稳定性，Me/Mn越大，系统越容易失稳。同时，Me/Mn=0.5和1 的工况下，结构无条件稳定域分别出现在-0.078 ＜Me/Mn-Ke/Kn＜0.075和Ke/Kn≈1 ，因此，可以得出结论，在Me/Mn＜1的条件下，当且仅当Me/Mn-Ke/Kn≈0时，系统有无条件稳定特性。与只考虑物理子结构的质量或只考虑物理子结构的刚度比较，可以发现同时考虑物理子结构的刚度和质量后，系统不再是简单的随着质量比或者刚度比增大而稳定性降低。说明了该系统受质量比与刚度比这两个参数的耦合作用影响。

图5 实时子结构的时滞稳定域(Ce=0)Fig. 5 Delay stability region of RTST (Ce=0)

2.3 阻尼之比作为自变量的稳定性探究

当以物理子结构与原结构的阻尼之比作为变量时，同样也研究了四种工况：1)Ke=0 ；2)Ke/Kn=0.5 ；3)Ke/Kn=1 ；4)Ke/Kn=2。

图 6(b)为工况1 仅考虑物理子结构的阻尼时结构的稳定域图像，可以看出，当阻尼之比Ce/C＜0.5时，系统始终是无条件稳定的，当Ce/C＞0.5后，系统随时滞增加呈现出周期性的稳定性切换现象，同时，稳定区域随着时滞增加越来越小。对该工况，并不存在小时滞情况，故近似方法并不适用于该工况。其余两种方法对比的结论与第2.2 节刚度之比为自变量时，工况1 的稳定性变化规律类似，不再赘述。

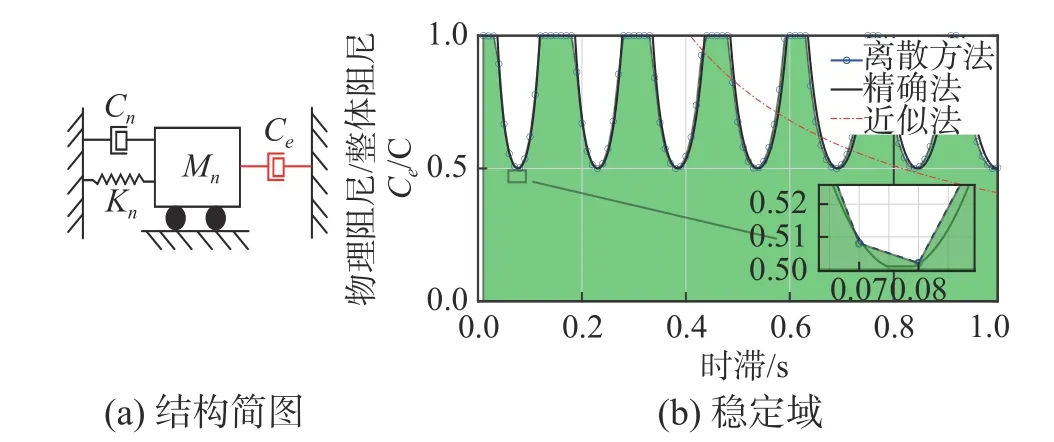
图6 实时子结构的时滞稳定域(Me=0, Ke=0)Fig. 6 Delay stability region of real time substructure (Me=0, Ke=0)

图7 分别为工况2～工况4 对应的稳定域图像，对比三幅图可以看出，随着Ke/Kn不断增大，系统的稳定域越来越小，即结构越来越容易失稳。由于研究中选取的积分步长为0.01 s，使用离散方法进行研究时，时滞最小只能取至与积分步长相同，故该积分步长下，离散方法无法直接判断时滞小于10 ms 时结构是否稳定，而当时滞小于10 ms 时，三幅图中都存在一条使用精确方法绘制出的临界时滞曲线，由于该区间内时滞较小，故认为这条曲线左侧都是稳定的，并用阴影区域表示，即该稳定区域是通过精确方法获得的。同时，可以观察到每幅图中的临界时滞曲线近似可以看做多条平行的竖向线段，即系统的稳定性受阻尼之比影响很小，反而对刚度比更加敏感。故可以认为在设计实时子结构试验时，阻尼之比不起到决定性的影响作用。

图7 实时子结构的时滞稳定域(Me=0)Fig. 7 Delay stability region of real time substructure (Me=0)

可知精确方法得到的最左侧的临界时滞曲线与近似方法绘制的近似临界时滞曲线吻合程度较高。充分说明近似方法只能满足小时滞情况，当时滞较大时，近似方法与其他两种方法都无法准确判定稳定性。

2.4 阻尼比和积分时间步长对稳定性的影响探究

为说明阻尼比与积分步长对单自由度实时子结构稳定性的影响，取图4(a)结构模型进行研究。图 8 为阻尼比分别为0.03、0.05 和0.10 时的时滞稳定域图像。可以看出不同阻尼比的结构稳定域轮廓基本一致，但系统的稳定域会随着阻尼比的增大而增大，说明增大结构的阻尼可以提高系统的稳定性。

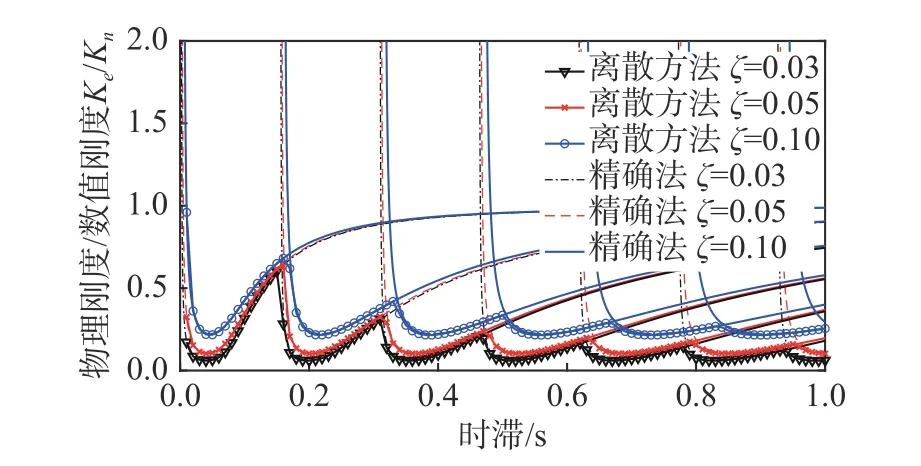
图8 不同阻尼比条件下结构稳定域Fig. 8 Stability region of an SDOF system with different damping ratios

图9 为积分步长分别为0.01 s、0.02 s 和0.03 s时结构的时滞稳定域图像。从图9 可以看出，当积分步长为0.01 s 时，精确法和离散方法绘制的稳定域基本一致，随着积分步长增大到0.02 s 和0.03 s后，离散方法得到的稳定区域显著降低，与连续方法得到的稳定区域差异也逐渐增大。说明了当积分步长小于或等于0.01 s 时，不需要考虑积分算法对稳定性的影响；反之，当积分步长大于0.01 s后，就不得不考虑积分算法对稳定性的改变，此时应该使用更为保守安全的离散稳定性分析方法。

图9 不同积分步长下的结构稳定域Fig. 9 Stability region of an SDOF system with different with different integration steps

3 数值验证

为了验证本文得到的结果，本文搭建了单自由度实时子结构仿真模型进行仿真验证，Simulink模型如图 10 所示。

图10 时滞系统Simulink 模型Fig. 10 Simulink model of delay system

取物理子结构仅考虑刚度的工况绘制的稳定域图像上“●”标记点进行数值模拟，如图 11 所示，即刚度比Ke/Kn=0.3，时滞为80 ms、130 ms和200 ms。积分步长取1/1024 s，激励方式为单位脉冲，得到结构的脉冲响应如图 12 所示。

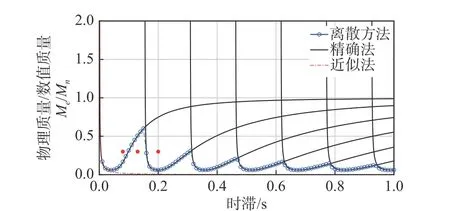
图11 数值模拟验证工况Fig. 11 Numerical simulation verification case

图12 反应的是结构在不同时滞情况下的单位脉冲响应。结构位移响应呈现发散的趋势，则说明系统是不稳定的。从图中可以看出该单自由度实时子结构系统在时滞为80 ms 和200 ms 时位移是发散的，在时滞为130 ms 时位移是收敛的。即系统在80 ms 是失稳的，当时滞增大至130 ms，系统又进入了稳定状态，当时滞进一步增大至200 ms系统再次失稳。说明随着时滞增大，系统出现了稳定性切换现象。该数值模拟得到的结论与理论分析得到的结论相同，证明了本文理论的可靠性。

图12 结构的单位脉冲响应Fig. 12 Impulse response of structure

4 试验验证

4.1 SDOF 稳定性验证试验

本文进行了单时滞源的RTST 实测。试验设备为滨海土木工程与安全教育部重点试验室的MTS伺服液压作动器，该作动器本身存在时滞，时滞大小约为21/1024 s。试验中的数值计算通过控制器完成，积分步长取1/1024 s，积分方法为CR 积分算法。如图 13，试验模型为SDOF 结构，取结构的部分刚度作为物理子结构。考虑到失稳会造成构件和试验设备造成不必要的损失，故物理子结构也通过数值建模，作动器加载端不放置实际的构件。而物理子结构为线弹性结构时，物理子结构的反馈力即弹性力，因此只需要将作动器的位移信号作为反馈信号反馈给数值子结构即可。

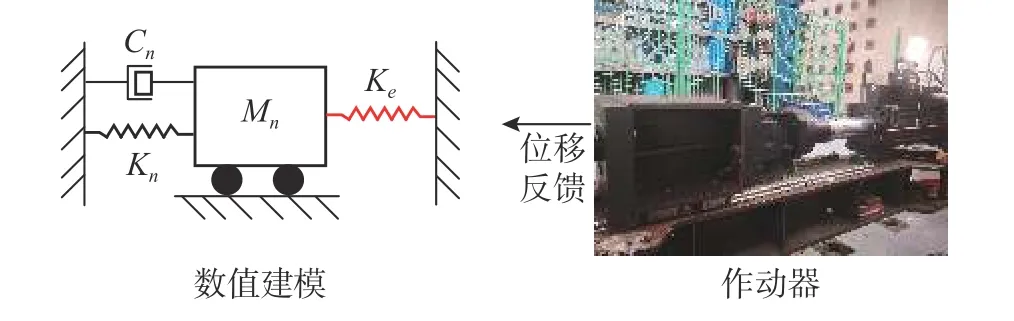
图13 实时子结构试验加载装备Fig. 13 Facility for real-time hybrid testing

采用反补偿方法[19]对作动器时滞进行补偿，补偿后该实时子结构系统的时滞减小至约3 ms。由于结构的体量较小，且物理子结构是通过数值建模的线弹性结构，因此可以在位移反馈信号中使用Simulink 提供的delay 模块，进而达到改变时滞大小的效果。取结构参数如表 2，此时结构划分情况为Ke/Kn=1/10。使用本文提出方法计算并绘制出不同时滞下控制极点分布图，如图 14 所示。

表2 结构参数Table 2 Structural parameters

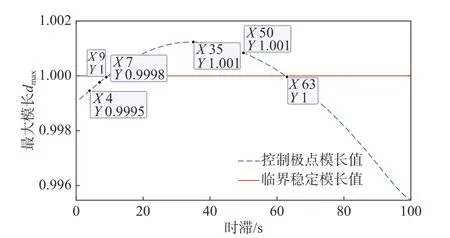
图14 不同时滞下控制极点模长图Fig. 14 Norm of the control poles with different time delay

图14 中纵坐标为控制极点的模长，横坐标为系统时滞，控制极点模长大于1 时系统失稳，模长小于1 时，系统稳定。由图14 可以看出在该划分情况下，系统时滞在9 ms～63 ms 是失稳的，其余时滞区间内是稳定的，故取图14 上标记的6 个不同时滞进行实测，试验中结构参数和工况分别如表 2 和表 3，试验激励为周期为4 s 的正弦激励。

表3 试验工况Table 3 Test conditions for SDOF test

图 15 为不同时滞下试验结构的位移响应，图中深实线为命令位移，浅虚线为测量位移。可以看出，当时滞为4 ms 时，结构的位移响应呈现出等幅震荡的现象但没有发散，说明该时滞下系统接近于临界稳定；当时滞增大至20 ms、35 ms、50 ms 时，这三种时滞下的测量位移都呈现出高频振荡和发散现象；而增大时滞至90 ms 时，结构的测量位移收敛。说明当时滞为4 ms 和90 ms时，该单自由度实时子结构系统是稳定的，时滞为20 ms、35 ms 和50 ms 时，该系统失稳。因此，试验结果与理论分析得到的稳定状态是一致的。通过该试验证明了单自由度实时子结构存在稳定性切换现象，随着时滞增大，该单自由度实时子结构从稳定状态进入不稳定状态，当时滞进一步增大后，又从不稳定状态回到了稳定状态。图 15(b)为时滞7 ms 的试验结果，从图上可以看出该时滞下结构的的测量位移出现了高频震荡的现象，最终在13 s 时失稳了。该试验结果与理论分析相反，该时滞下结构应该是稳定的，其位移响应不应该呈现发散的状态。该工况下理论与试验结果不符可能是因为试验中存在的噪声等干扰会对结构的稳定性造成影响，另一方面，作动器的时滞是在小范围内波动的而不是恒定不变的，故在该工况下，该实时子结构系统的时滞已接近或超过临界时滞(9 ms)，故导致最终发散。

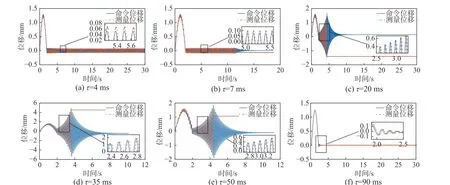
图15 试验结果Fig. 15 Test results

4.2 2DOF 稳定性验证试验

在SDOF 试验的基础上进行2DOF 稳定性验证试验，将2DOF 上层结构作为数值子结构，下层作为数值子结构，如图 16 所示。物理子结构为一单层框架结构，其参数为：质量Me=5 kg，刚度Ke=5500 N/m，底部应变与顶部剪力的对应关系为f(t)=68 000ε(f(t)为剪力，ε 为柱脚应变)。注意，物理子结构的惯性力应该扣除以得到物理子结构应当反馈给数值子结构的反力真实值。

图16 2DOF 试验Fig. 16 2DOF test

试验工况见表 4，激励为El Centro 地震动，试验中积分步长取值为1/1024 s。试验结果如图 17 所示。

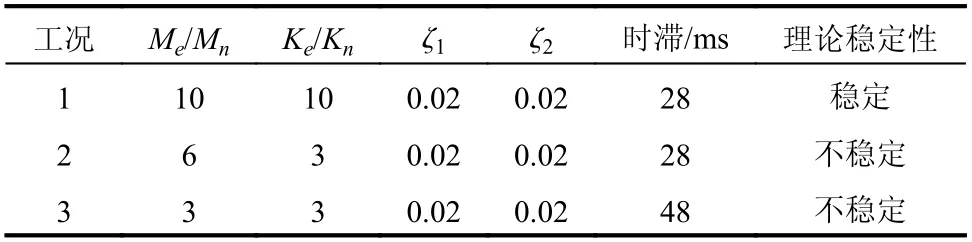
表4 试验工况Table 4 Test conditions for 2DOF test

从图 17 可以看出，当Me/Mn=Ke/Kn=10，2DOF在时滞28 ms 时的测量位移与目标位移几乎完全吻合，且位移呈现收敛的趋势，说明2DOF 在该划分参数和时滞下处于稳定状态，与理论稳定分析结果一致。当Me/Mn=6、Ke/Kn=3 而时滞为28 ms时，命令位移与测量位移在5 s 前吻合较好，5 s后测量位移呈现高频振荡并发散的趋势，说明该划分方式相应时滞情况下2DOF 系统是失稳的。当Me/Mn=3、Ke/Kn=3 而时滞为48 ms 时，测量位移与命令位移在2 s 后迅速呈现发散的现象，说明该工况下2DOF 失稳严重。三种工况下的试验结果都与理论分析结果吻合，工况1 和工况2 结果对比可知，当时滞相同时，2DOF 的稳定性会随着结构划分情况变化而变化，因此在2DOF 试验中，适当的调整数值子结构占原结构的比例可以保证试验的稳定性。

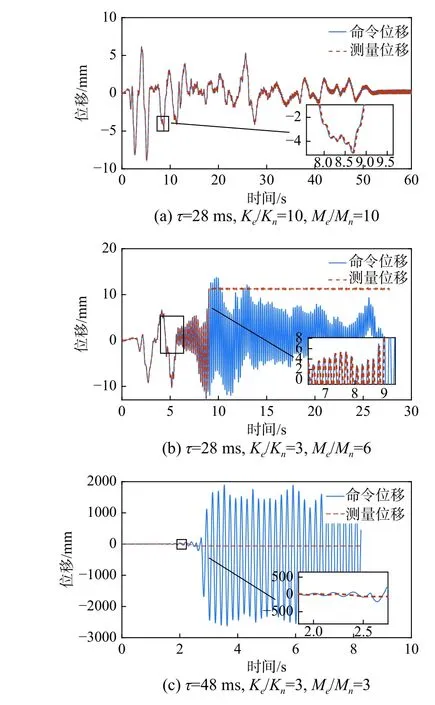
图17 2DOF 试验结果Fig. 17 2DOF test results

5 结论

本文建立了RTHS 基于积分算法的离散稳定性分析方法，并使用提出方法与已有的连续稳定性分析方法研究了结构划分参数、阻尼比、积分步长对结构稳定性的影响，模拟和实测对比了两类方法的结果，证明了所提出方法的正确性和可靠性。

(2) 对每一种结构划分方式，会存在多个时滞稳定区域，说明结构随着时滞的增加，在稳定状态与不稳定状态进行变换。即使时滞很大时，结构也可能是稳定的。实际研究中，一般最关心第一次出现稳定性变换时(即第一次发生失稳现象)的临界时滞。

(3) 对比三种方法可知，近似方法仅适用于小时滞情况(τ＜1 ms)。当积分步长小于或等于0.01 s，不需要考虑积分算法对稳定性的影响，可以直接使用精确法研究结构的稳定性；反之，当积分步长大于0.01 s，必须考虑积分算法对稳定性的影响，此时应该使用更为保守安全的离散稳定性分析方法，本文方法即是。

(4) 经RTHT 试验检验，本文所提出离散化方法对多自由度问题也有正确的效果，但相关研究拟于后续开展。本文方法目前仅对线性系统进行了验证，后续会对更为复杂的非线性系统展开研究。