不同海况下漂浮式风电场大型化响应分析

李蜀军， 岳敏楠， 王 博， 李 春,2， 丁勤卫

(1．上海理工大学 能源与动力工程学院，上海 200093；2．上海市动力工程多相流动与传热重点实验室，上海 200093；3．中国联合重型燃气轮机技术有限公司，北京 100020)

我国风电发展迅速，截至2019年累计风电装机容量达236.7 GW，已成全球最大风电装机国[1]。陆上风电存在远离用电负荷中心、运输不便、输送损耗高等缺点，因此距经济中心更近、风质更优的海上风电是未来风电发展的重要方向。对于水深范围更广、风能储量更大的深水区，成本更低、水深适应性更好的漂浮式风力机更具经济优势和竞争性[2]。

按平台稳定性获得的方式不同，广泛使用的漂浮式平台有驳船式(Barge)、立柱式(Spar)、张力腿式(Tension Leg Platform, TLP)及半潜式(Semi-Submersible, S-S)[3]。其中，驳船式平台水线面面积大、稳定性好、建造和维护方便，前景广阔。

因基础不固定，在风波激励下，漂浮式风力机平台始终处于运动状态，产生的摇荡运动直接影响风力机发电性能，恶劣海况下甚至威胁设备安全[4]。提高漂浮式风力机稳定性，增强其在各种海况下的抗风浪能力一直是国内外研究的热点。迄今，已有学者针对上述问题在以下几方面展开研究：(1) 变桨控制。Chujo等[5]用水池实验的方法进行漂浮式风力机变桨控制实验；周腊吾等[6]提出一种基于神经网络的独立变桨控制方法，通过FAST-Simulink联合仿真，验证了该控制方法更能有效地减小风载荷波动和降低平台纵摇响应。(2) 安装垂荡板和增加平台吃水。Yue等[7]采用Fortran语言实现AQWA二次开发，研究风波耦合作用下垂荡板及其安装位置对Spar平台响应的影响。黄致谦等[8]通过半潜平台下部附加水箱以增大平台吃水深度，结果显示新平台较原半潜平台有更佳的垂荡、横摇及纵摇稳定性。(3) 配置调谐质量阻尼器(Turned Mass Damper, TMD)。当漂浮式风力机受到外部激励时，TMD系统产生与结构运动相反的力，同时通过阻尼系统吸收主体结构振动能量，达到对结构稳定控制的目的。Yang等[9]建立应用于Barge平台的TMD模型，研究其减震效果，结果表明TMD可有效抑制平台纵摇响应。丁勤卫等[10]对Barge平台TMD参数(阻尼、质量及刚度)进行优化。

但以上方法均存在一定不足：(1) 变桨调节只能在一定风速范围内实现叶片减载，当风速大于切出风速时，调节失效[11]。(2) 安装垂荡板会增加平台造价，降低其经济性；此外，垂荡板和阻尼板使用范围限制性较大[12]。(3)TMD需在风力机内部配置1%～5%塔架质量的质量块，这会占用较大的机舱空间，且TMD控制频带窄，当风力机因结构损伤等原因导致其固有频率改变时会发生失调[13]。基于共用系泊组建漂浮式风电场不受环境约束、不受平台种类限制、不占据风力机空间、不增加平台造价，且可同时提高多个漂浮式风力机稳定性，是提高漂浮式风力机平台稳定性的可行手段。丁勤卫等[14-15]已通过数值计算证明其可行性。目前研究仅限于2×2及3×3阵列漂浮式风电场平台响应特性。对于迅猛发展的风电而言，大型化、规模化是风电发展的必然趋势。故研究更大规模漂浮式风电场可行性及其阶数增大对平台稳定性的影响具有重要意义。为此，笔者建立Barge单平台和基于Barge平台的2×2、3×3、4×4和5×5阵列漂浮式风电场，分析不同海况下风电场阶数增大对平台稳定性的影响，以期为工程应用提供参考。

1 研究对象

1.1 漂浮式风力机

漂浮式风电场基于Barge平台漂浮式风力机。其中，风力机选取NREL 5 MW风力机[16]，漂浮式平台选择ITI Energy Barge平台。风力机和平台主要参数分别见表1和表2[17]。

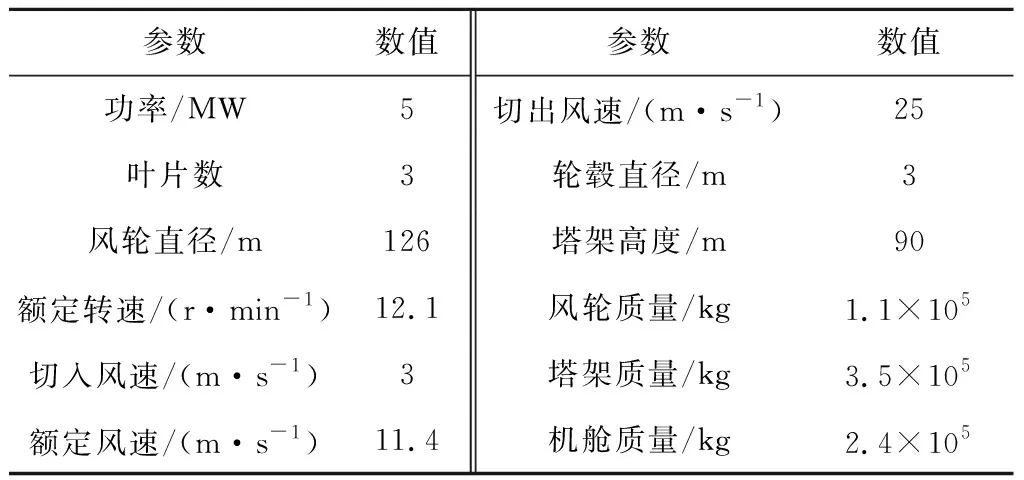
表1 NREL 5 MW风力机参数

表2 ITI Energy Barge平台参数

1.2 漂浮式风电场

本文中风电场基于共用系泊组建，且漂浮式风力机间呈正交排列。考虑到相近风力机之间会互相干扰，需合理设置风力机间距，风力机间距均取500 m。Barge平台漂浮式风力机如图1(a)所示，2×2、3×3、4×4及5×5阵列风电场如图1(b)所示。

(a) 单平台

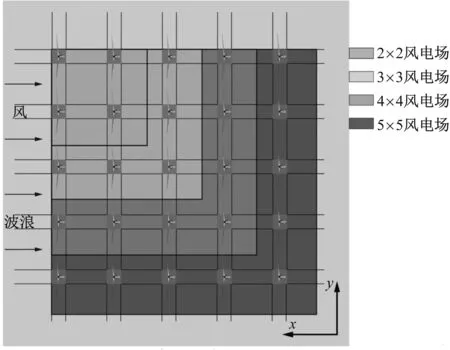
(b) 风电场平台图1 单平台与风电场平台Fig.1 Single Barge and wind farm platforms

系泊包括固定悬链线和链接悬链线，图2为漂浮式风电场系泊侧向局部水下视图。其中，系泊参数见表3。

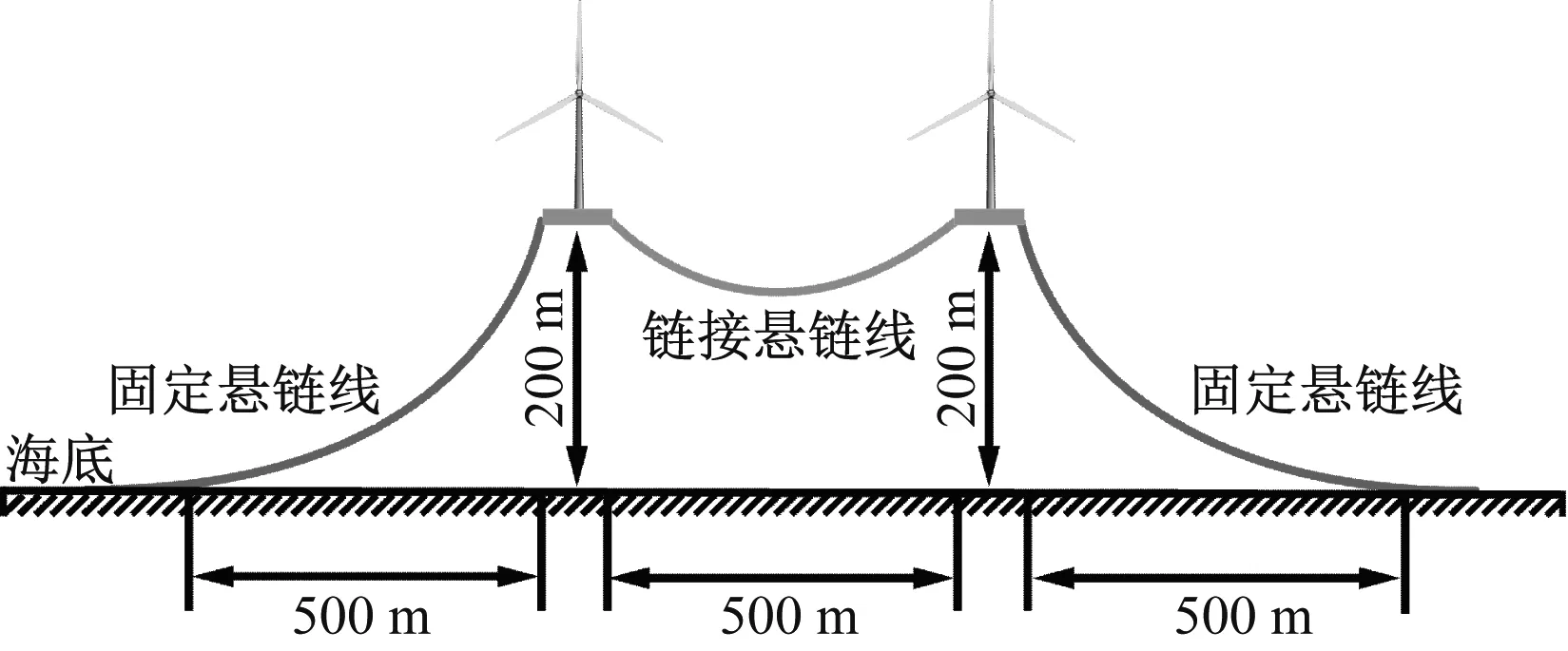
图2 系泊示意图Fig.2 Mooring diagram

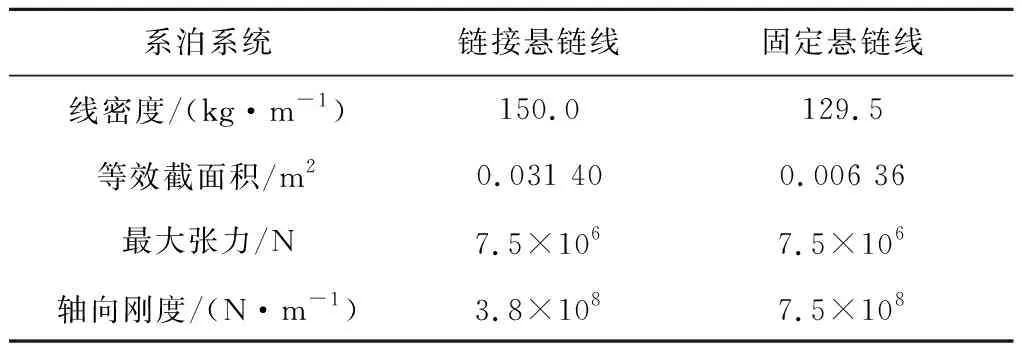
表3 系泊参数Tab.3 Mooring parameters

2 海况与载荷

漂浮式风力机在海上受到的载荷复杂多变，如风、波浪、流及浮冰等[18]。其中，风载荷与波浪载荷是影响漂浮式风力机动态响应的主要载荷，故主要考虑风载荷与波浪载荷的作用。考虑到水动力软件AQWA广泛用于海工平台响应分析，但其无法实现风力机所受风载荷的精确求解；FAST(Fatigue，Aerodynamics，Structure，Turbulence)可实现漂浮式风力机单平台波浪载荷和风载荷的求解，但无法求解多体问题。笔者基于AQWA，将FAST中气动力导入AQWA，进而实现在风波作用下风电场平台动态响应的求解。

在役海况下，漂浮式风力机同时受到风、波浪载荷作用，使用联合分布可更合理地描述风和波浪间的参数关系[19]。根据Johannessen等对实际海域风、波浪参数的测定[20]，提出风波联合分布函数f(u10,HS,Tp)：

f(u10,HS,Tp)=fU(u10)·fHS|U10(HS|u10)·

fTp|HS U10(Tp|HS,u10)

(1)

式中：fU(u10)为边缘分布函数；fHS|U10(HS|u10)和fTp|HS U10(Tp|HS,u10)均为条件概率函数；u10为距海面10 m高度处1 h平均风速；HS为有义波高；Tp为跨零周期。

给定u10，有义波高HS和跨零周期Tp的期望值如下：

(2)

(3)

式中：α为形状参数；β为比例参数；Γ为伽马函数。

考虑风切变，则平均风速Uw(z)与海面高度z的关系为：

(4)

式中：Uref为参考风速；zref为参考风速高度，此处取10 m。

为验证风电场海上长期在役环境中不同海况下稳定性，分别取NREL 5 MW风力机切入风速、额定风速、切出风速与满足上式波浪参数海况，具体参数见表4。

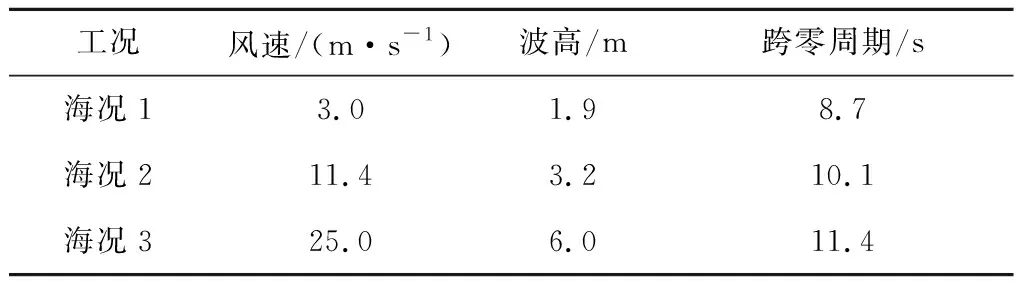
表4 海况参数

2.1 风载荷

考虑到实际海洋环境中风场具有一定湍流度，通过国际电工委员会(IEC)中定义的Kaimal湍流风谱模型生成风场，其功率谱密度S(f)为：

(5)

在选定风速下，由Kaimal湍流风谱生成风速时间序列曲线，如图3所示。

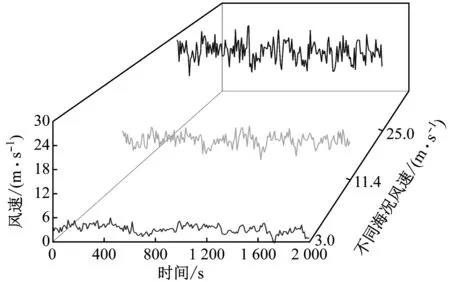
图3 风速时间序列Fig.3 Time series of wind speed

风载荷的求解基于叶素动量理论。将叶片沿展向分为多个叶素，求解每段叶素上诱导因子和诱导速度，结合各项气动参数，对气动力沿叶展积分，得到整个叶片受力。其中，第i段叶素速度三角形及受力如图4所示。

第i段叶素相对速度W、来流攻角αi及入流角γ可表示为：

(6)

αi=γ-βi

(7)

(8)

式中：U∞为来流风速；Ω为风轮转速；r为该段叶素距轮毂中心间距；a与b分别为轴向和切向诱导因子；βi为桨距角。

叶素受到的扭矩Q与推力N为：

(9)

式中：ρ为空气密度；c为叶片弦长；Cl为升力系数；Cd为阻力系数。

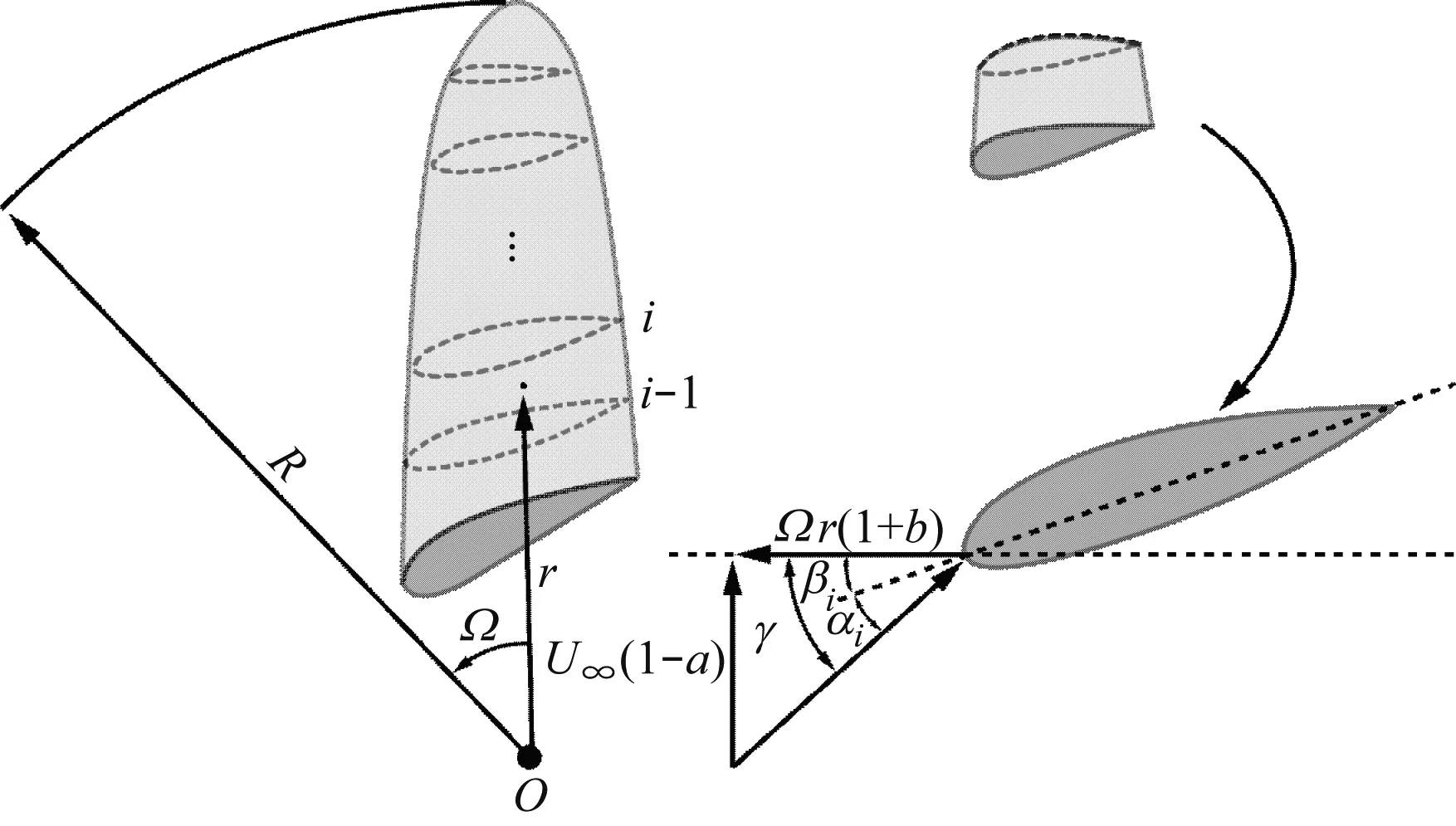
图4 叶片截面及速度三角形Fig.4 Blade section and velocity triangle

2.2 波浪载荷

波浪可视为由方向、频率、振幅及相位各异的规则波组成的，海洋工程中一般使用波浪谱描述波浪能量分布，反映波浪特征。选用P-M谱生成不规则波，P-M谱与波高表达式为[21]：

(10)

(11)

式中：θ为相位角；Ak为随机波波幅；εk为初始相位角；t为时间。

不同海况下波浪能量谱密度及波高时间序列如图5所示。

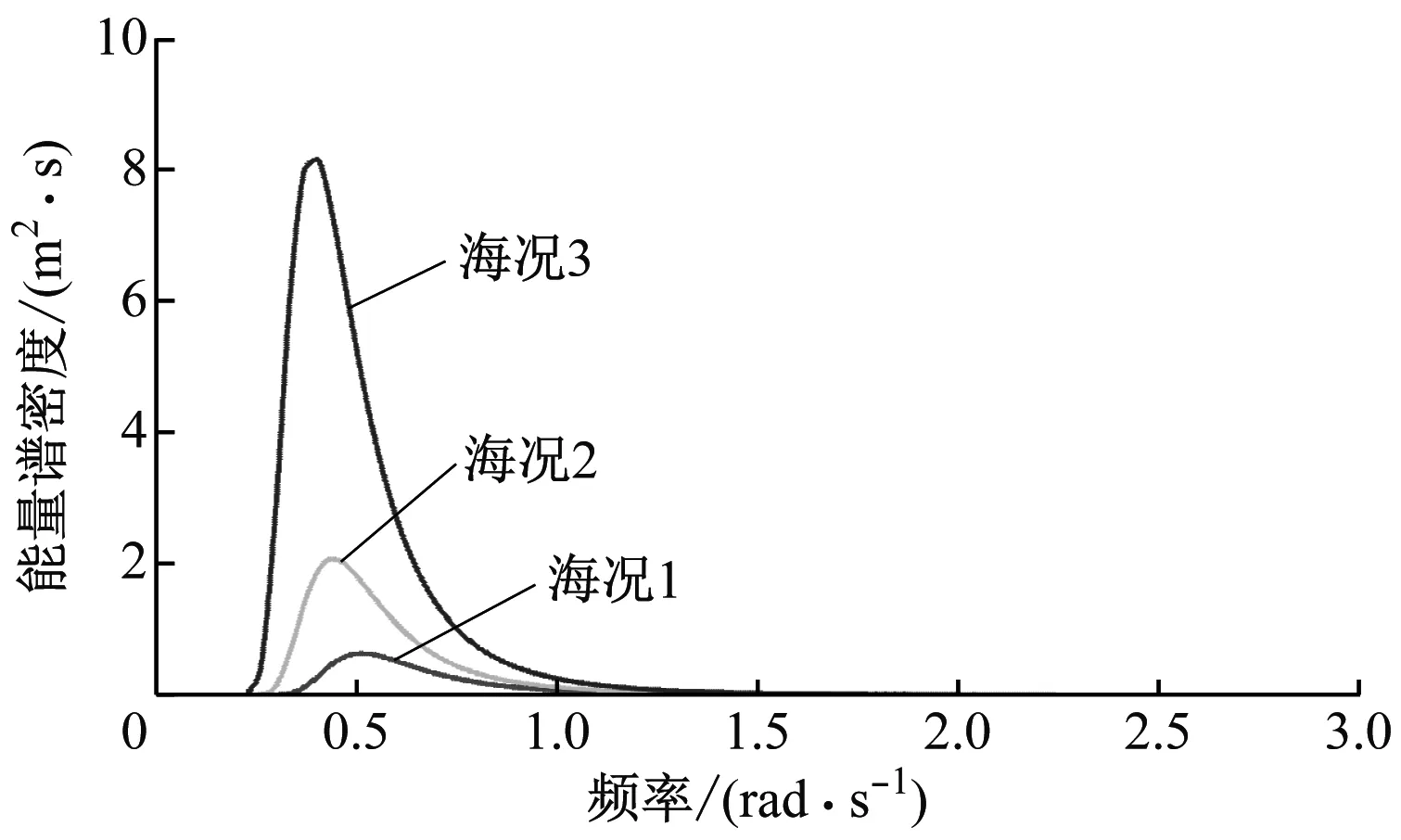
(a)

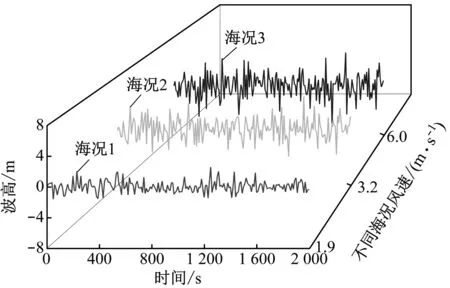
(b)图5 能量谱密度与波高时间序列Fig.5 Power spectral density and time series of wave height

多浮体水动力数值模拟有势流线性法、势流非线性法及黏性法[22]。势流非线性法求解需时时更新自由液面和物面网格，计算量大；黏性法对计算要求较高，仅用于极限海况下海工平台生存能力分析；线性势流法假定流体为不可压缩无黏势流，在此前提下求解效率较大提高，在波浪对多浮体作用研究方面应用广泛[23]。故本文采用线性势流法，考虑Barge平台对入射波的影响，基于辐射绕射理论求解波浪载荷。速度势函数φ可表示为：

(12)

式中：φi为入射势；φd为绕射势；φr,j为辐射势。

速度势函数需满足拉普拉斯方程和海底、自由液面、湿表面及无穷远处边界条件：

(13)

式中：g为重力加速度；η为入射波波面函数；n为浮体湿表面外法向量。

求得速度势函数后，由线性伯努利方程求得一阶波浪力Fw为：

(14)

式中：ρw为海水密度。

求出一阶波浪力后，对整个湿表面积分即得到单位波幅作用下平台所受水动力，再对不同方向、频率及振幅的规则波叠加，求得波浪载荷。

3 控制方程及平台自由度

3.1 控制方程

求解波浪载荷需给定波面边界条件。随水深变化需采用不同波浪理论，有适用于浅水区的孤立波理论和深水区的线性微幅波浪理论。漂浮式风力机工作在深水区，故采用线性微幅波浪理论，频域运动方程为[24]：

[M+M(ω)]·f″(ω)+C(ω)·f′(ω)+

K·f(ω)=F(ω)

(15)

式中：M、M(ω)分别为平台质量矩阵和附加质量矩阵；C(ω)、K分别为平台阻尼矩阵和刚度矩阵；f″、f′和f为平台加速度、速度和位移；F(ω)为平台受到的波浪激振力。

在风载荷与波浪载荷共同作用下，漂浮式风力机单平台时域运动方程可表示为：

[M+M(∞)]f″(t)+Cf′(t)+Kf(t)+

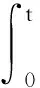
(16)

式中：M(∞)、C及K为平台附加质量矩阵、阻尼矩阵及刚度矩阵；R(t-τ)为迟滞函数；F(t)为平台受到的载荷。

与漂浮式风力机单平台不同，风电场平台的运动除受风、波浪及系泊影响外，还存在平台与平台间耦合运动，致使漂浮式风电场平台运动响应更为复杂。在风载荷与波浪载荷共同作用下，漂浮式风电场平台时域运动方程可表示为：

(17)

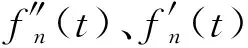
3.2 平台自由度

在风载荷与波浪载荷共同作用下，漂浮式风力机平台在海面上会发生6个自由度上的运动，其中包括绕着各轴(x轴、y轴及z轴)的转动，即横摇、纵摇及艏摇；沿各轴的平动，包括纵荡、横荡及垂荡。风浪均由-180°方向入射，平台在6个自由度上的运动如图6所示。

4 可靠性验证

平台网格划分是否满足水动力计算要求，可通过对比远场法与近场法对二阶波浪力计算结果来验证。当远场法与近场法求得的结果相近时，可认为网格划分满足水动力计算要求。计算中需对水线面下绕射单元进行网格加密。因此，水线面以上网格最大尺寸取1 m，水线面以下网格最大尺寸取0.5 m，共划分网格约8 000个，其中绕射单元网格数约为5 000，Barge平台漂浮式风力机网格划分如图7所示。

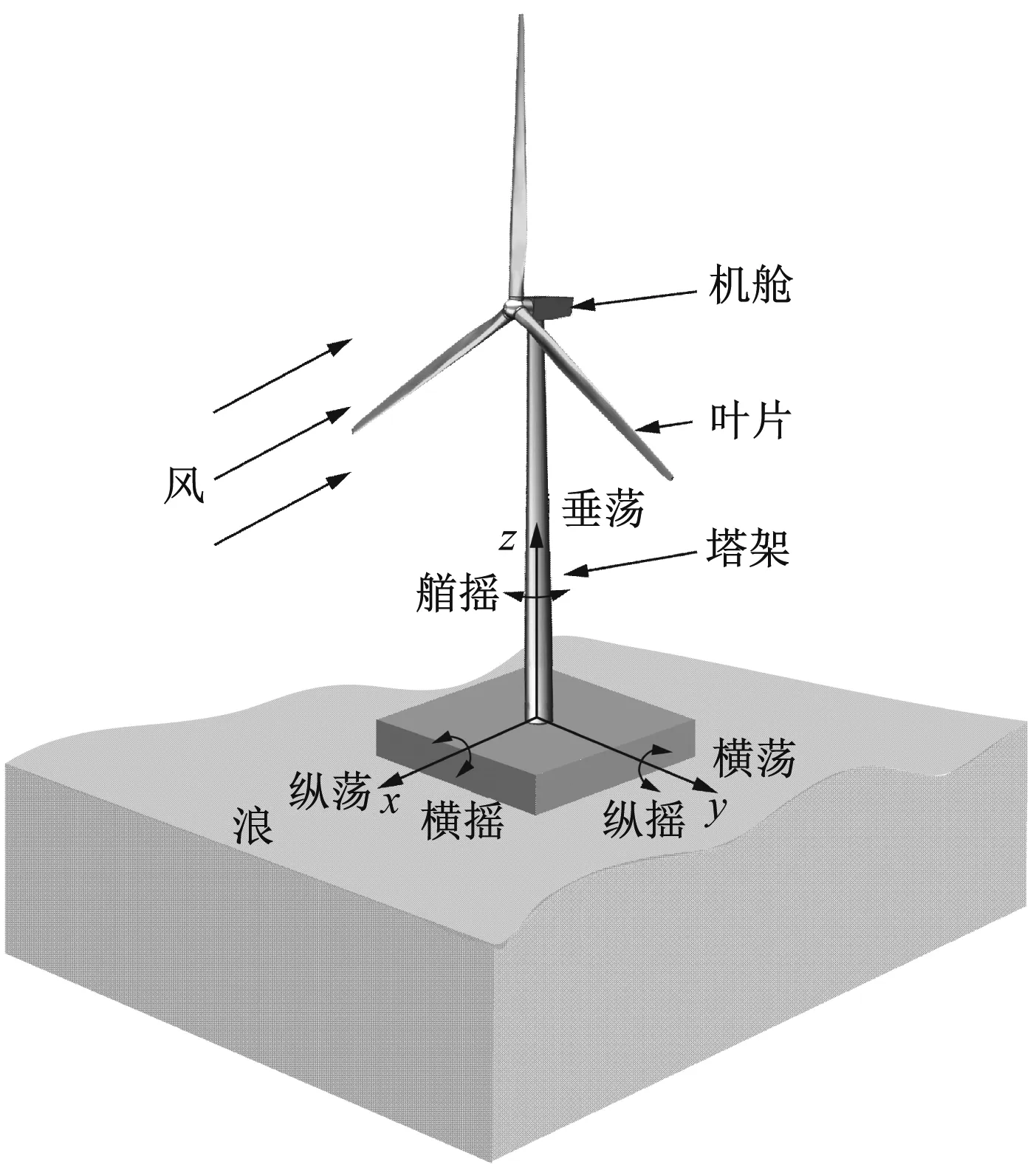
图6 平台自由度Fig.6 Platform freedom

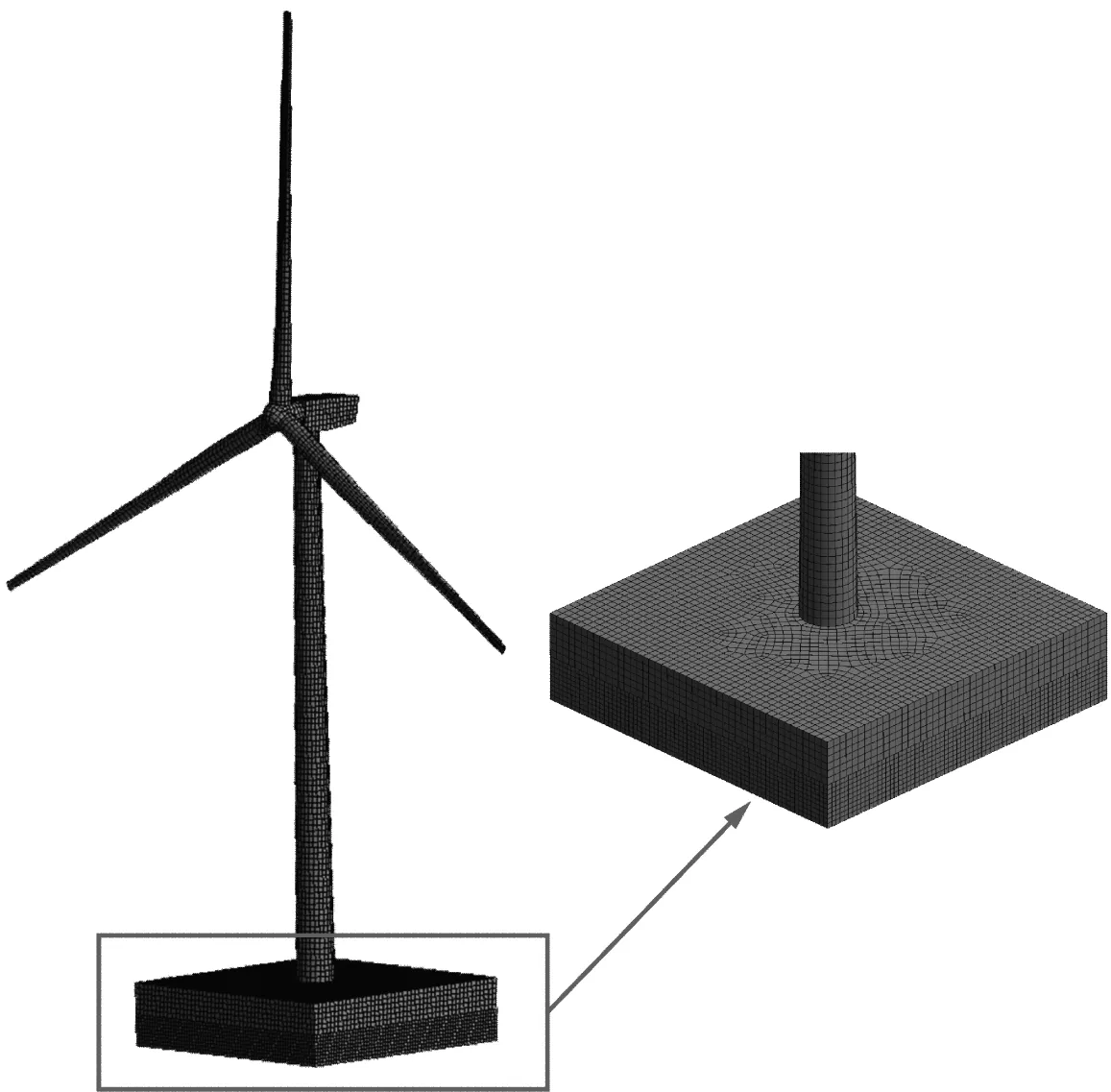
图7 Barge平台漂浮式风力机网格划分Fig.7 Floating wind turbine grid discrete of the Barge platform

分别采用远场法与近场法求得纵荡自由度上漂浮式风力机平台平均漂移力，如图8所示。由图8可知，二者均随波浪频率增大而逐渐增加，在频率为1.2 rad/s附近达到最大值。之后远场法与近场法计算结果虽存在一定差异，但趋势大致相同，且两者差异随频率增大越来越小，并逐渐趋于一致，故可认为网格划分满足计算要求。

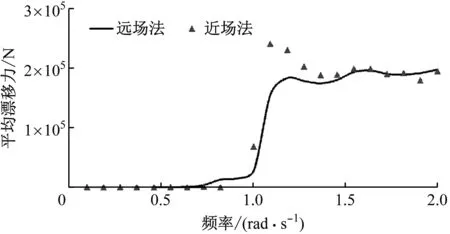
图8 纵荡二阶平均漂移力Fig.8 The second-order average drift force of surge

5 结果与分析

漂浮式风电场由多个平台和系泊系统组建而成，平台除受风浪载荷影响外，还需考虑平台间因系泊连接导致的耦合运动，即响应剧烈平台会通过悬链线系泊影响到相邻平台的动态响应。故先以3×3阵列风电场平台为例，分析其在海况2下动态响应及系泊受力特性，进而为后文不同阶风电场间的对比提供依据。

5.1 3×3阵列风电场平台响应分析

图9为3×3阵列风电场平台在额定风速海况下的轨迹图，其中P1、P2和P3为风浪入射侧平台，P7、P8和P9为背风浪侧平台，P4、P5和P6为前两列平台的中心列平台。

由图9可知，以风浪入射方向为参考，漂浮式风电场平台P1、P4、P7和P3、P6、P9运行轨迹关于中心线对称。(1) 沿着风浪入射方向(纵向)，靠近入射侧平台纵荡位移明显较后方平台更大，越远离入射侧平台，纵荡稳定性越好。这是因为迎风侧平台在纵向除受风浪载荷作用外，还需通过系泊对后方平台提供水平方向拉力，而越远离风浪入射侧，需对后方平台提供的水平回复力越小。(2) 侧向系泊回复力受系泊长度、系泊与平台夹角的影响。随3×3阵列漂浮式平台发生纵向位移，中心线平台两侧受力平衡，故横荡位移极小；而随各平台纵荡位移的增大，两侧平台靠近外侧的固定系泊躺地长度减小，且平台与两侧系泊夹角增大，平台因侧向受力不均而发生横荡位移。

风电场平台整体上比单平台有更高的稳定性。额定风速下，3×3阵列风电场平台最大响应均值与单平台响应最大值见表5。

由表5可知，就风电场平台总体而言，除存在一定横荡响应外，在纵荡、垂荡及纵摇自由度上响应均小于单平台，稳定性更高。且横荡属平动位移，仅代表平台在海面上的位置变化，对风力机影响较小。纵摇角度大小则代表风轮进行俯仰运动的剧烈程度，会直接改变风轮有效迎风面积，从而影响风力机发电能力。由表5可知，风电场平台较单平台纵摇角度由10.5°减小至8.6°，稳定性提高了18.7%，这对于提高风力机发电能力和抑制其输出功率波动具有重要意义。

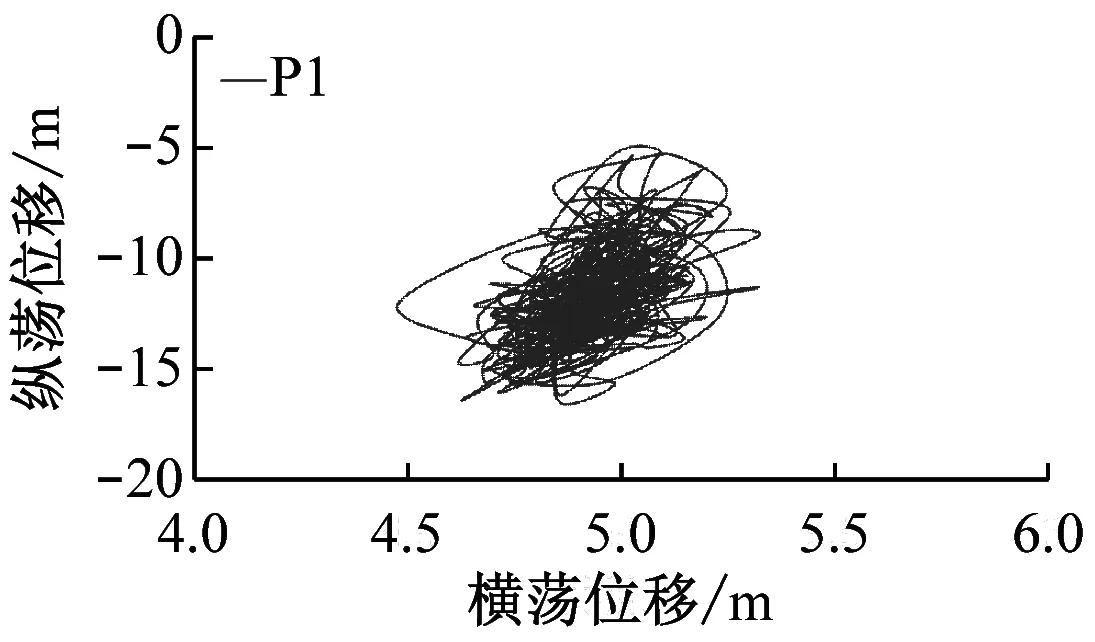
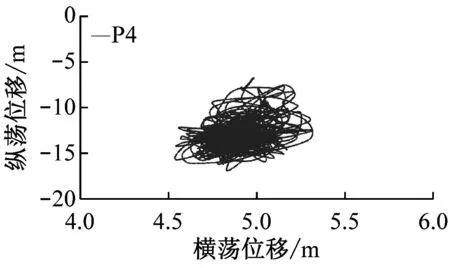
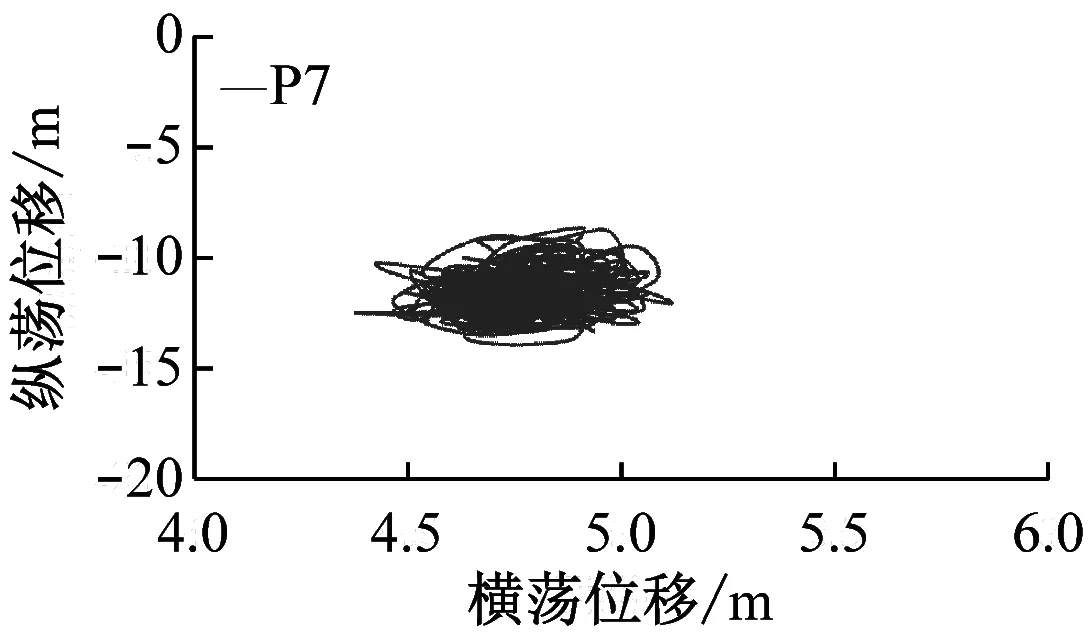
图9 3×3阵列风电场平台运动轨迹图Fig.9 Trajectory map of 3×3 array wind farm platforms

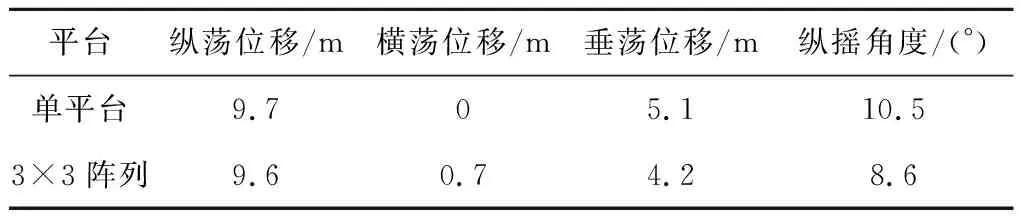
表5 单平台与3×3阵列风电场平台响应最大值对比

根据系泊位置及受力不同，将固定系泊分为迎风侧(前侧)、背风侧(后侧)、平行于载荷入射方向的风电场两侧(侧向)；将悬链线系泊分为平台提供平行于载荷入射方向回复力的纵向系泊以及为平台提供横向回复力的横向系泊。3×3阵列风电场平台与单平台不同位置系泊拉力如图10所示。

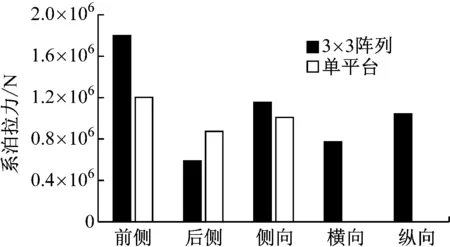
图10 单平台与3×3阵列风电场平台系泊拉力对比Fig.10 Comparison of mooring force between single platform and3×3 array wind farm platform

由图10可知，对于固定系泊，单平台及风电场平台系泊拉力均为前侧最大、后侧最小、侧向居中；对于风电场平台中的悬链线系泊，纵向系泊拉力较横向更大，但均小于前侧系泊，故应特别关注前侧系泊受力状况，确保其在整个在役环境下受力均在安全范围内。因此，后文中对不同海况下系泊安全性分析均针对前侧系泊展开。

5.2 平台响应对比

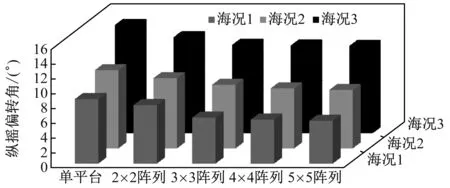
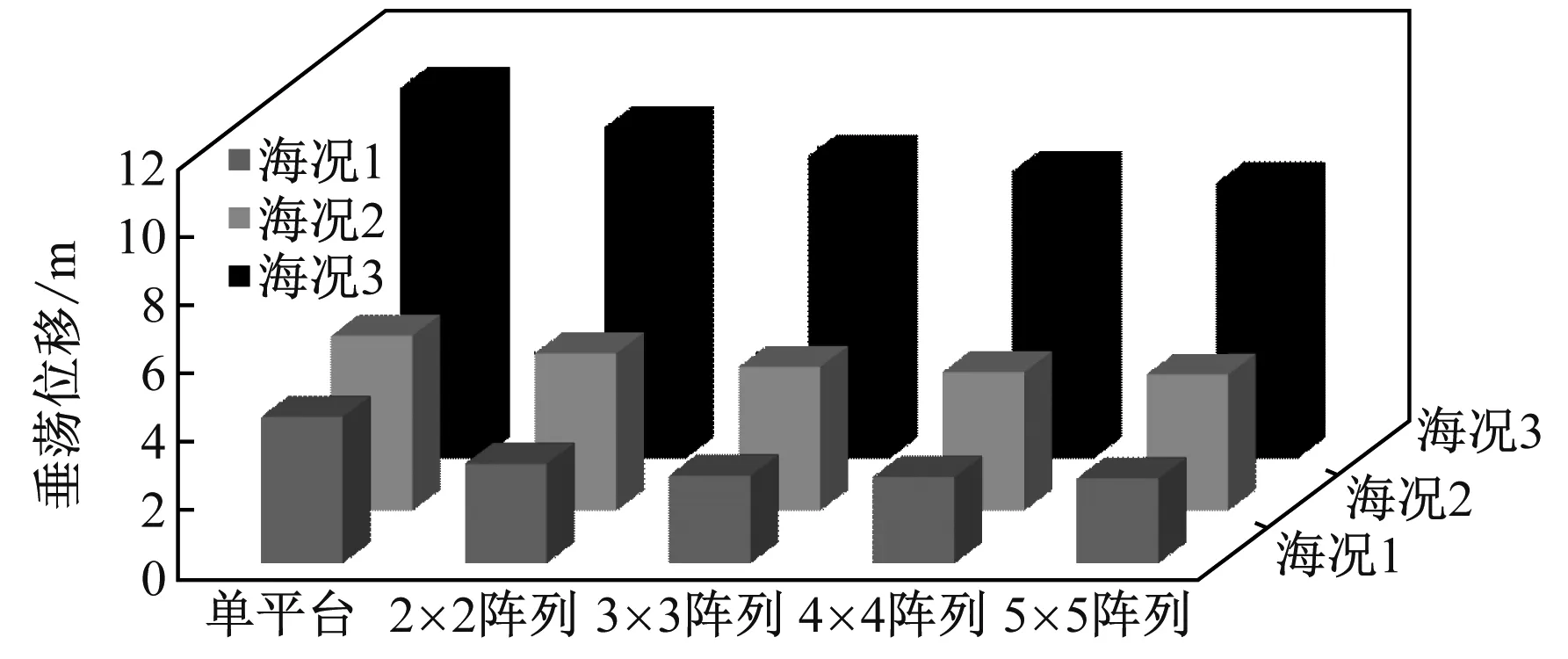
为分析单平台与风电场平台动态响应差异，对单平台与各阶风电场平台的纵荡、横荡、垂荡、纵摇响应及机舱加速度进行对比。此外，为验证各阶风电场平台对不同在役海况的适应情况，对比单平台及各阶风电场平台不同海况下的响应最大值，对比图及参数见图11。

由图11可知，随风电场阶数增加，平台在各自由度上的响应随之变化。(1) 在纵荡自由度上，随风电场阶数增大，平台响应总体呈减小趋势，仅2×2阵列风电场平台响应略大于单平台。这主要是由于2×2阵列风电场较简单，迎风侧平台响应较大，通过系泊将扰动传递到后侧平台，因而风电场平台整体纵荡位移较单平台偏大。但2×2阵列风电场平台垂荡及纵摇自由度较单平台有更高的稳定性，这主要是因为前侧平台的扰动力主要是水平方向，仅会对水平方向平动位移有较大影响。(2) 在横荡自由度上，风电场平台因平台纵向移动使其两侧受力不均而产生横荡位移，而单平台两侧受力始终一致，故单平台横荡位移极小。但总体而言，风电场平台横荡位移较小(小于1.4 m)，且横荡属平动位移，影响较小。(3) 垂荡和纵摇自由度上，平台稳定性随风电场阶数增大而提高，且当风电场大于3×3阵列后稳定性提高幅度减小。

(a)

(b)

(c)

(d)图11 单平台与各阶风电场平台动态响应对比Fig.11 Comparison of dynamic response among singleplatform and various wind farm platforms

此外，由图11还可知，随海况由切入风速增加至切出风速，单平台及各阶风电场平台在各自由度上响应均逐渐增大。除纵荡响应，3种海况下各阶风电场平台较单平台在纵荡、垂荡及纵摇自由度上均具有更高的稳定性，表明漂浮式风电场平台可适应更复杂的海域环境，且高阶风电场有更强的抗风浪能力。

机舱加速度可直接反映机舱受力大小，故文中以机舱加速度作为参照来研究塔顶响应，3种海况下单平台及各阶风电场机舱加速度如图12所示。

当机舱加速度大于6 m/s2时，其失效风险将增加。由图12可知，在切出风速海况下，单平台机舱加速度已达6.9 m/s2，需采取措施降低响应。而基于共用系泊的漂浮式风电场可有效降低平台机舱加速度，且随风电场阶数增大，机舱加速度减小，3种海况下风电场平台机舱加速度最大为5.68 m/s2，均在安全范围内，说明风电场平台较单平台可有效提高机舱安全性。

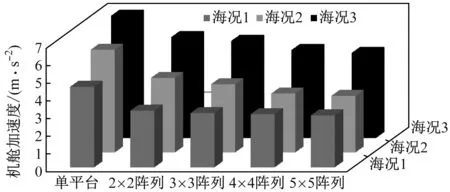
图12 单平台与各阶风电场平台机舱加速度的对比

5.3 系泊安全及经济性分析

系泊为漂浮式风力机提供海上定位和回复力，确保其受力在安全范围内是漂浮式风力机正常运行的前提。单平台与各阶风电场平台前侧系泊拉力见表6。

表6 单平台与各阶风电场平台前侧系泊拉力

海况改变和平台数量增加都会影响系泊拉力，海况2下前侧系泊在3种海况中拉力最大，故表6仅展示海况2下系泊安全系数。由表6可知:(1) 随风电场阶数增加，系泊拉力增大。这是由于平台增加使风电场平台承受较大风波载荷，在风波载荷同向入射时，前侧系泊需为平台提供更大水平回复力，因此前侧系泊拉力随风电场阶数增加而增大。(2) 随风速和波高增加，系泊拉力先增大后减小。这是因为当风速大于额定风速后，风力机叶片变桨使风轮推力减小。而海况3时已达变桨停机风速，此时风轮承受风载荷小，故前侧系泊拉力较海况2下小。虽然风电场平台较单平台前侧系泊拉力增大，如海况2时5×5阵列风电场安全系数只有3.2，但安全系数均远高于中国船级社(CCS)对系泊安全系数的要求，这也从侧面说明基于系泊组建漂浮式风电场是可行的。

6 结 论

(1) 风电场中风浪入射侧平台响应最剧烈，越远离入射侧,平台纵荡稳定性越好。

(2) 不同海况下，随风电场阶数增加，平台在纵荡、横荡、垂荡及纵摇自由度上的稳定性均逐渐增加，机舱加速度逐渐减小；虽风电场平台较单平台存在一定横荡响应，但横荡位移较小且属于平动位移，对漂浮式风力机影响较小。

(3) 漂浮式风电场中风浪入射侧系泊受力最大，且随风电场阶数增加，系泊拉力增大；3种海况中，额定风速海况下系泊受力最大，尤其需要注意此时系泊安全性。