江门中微子实验(JUNO)中心探测器结构在浮力下的整体稳定性研究

李华峰

(北京市建筑设计研究院有限公司， 北京 100045)

1 工程概况

江门中微子实验(JUNO)是大亚湾中微子实验的第二期工程，旨在设计、研制并运行一个国际领先的中微子实验站，以测定中微子质量顺序、精确测量中微子混合参数，并进行其他多项中微子科学前沿研究[1]，项目位于广东省江门市开平市金鸡镇打石山，距离阳江和台山反应堆均为53km。为了屏蔽宇宙射线，中心探测器被设置在地下约700m处。中心探测器整体形状为球形，置于直径约为43.5m，深44m的圆柱形水池中。

中心探测器主体不锈钢结构是江门中微子实验的核心装置。2015年7月JUNO合作组最终确定采用有机玻璃球+不锈钢网壳方案为主选方案，该方案中，中心探测器的内层结构为内径35.4m的有机玻璃球壳，该球壳通过一定数量的支撑杆连接在外层不锈钢球面网壳上，不锈钢网壳内径为40.1m。有机玻璃球内装有约2万t液体闪烁体(简称液闪)作为靶物质。不锈钢网壳上密布安装有约2万只20in光电倍增管和25 000只3in光电倍增管及相应的前段电子学，在有机玻璃球和不锈钢网壳之间以及不锈钢网壳和水池池壁之间均充满超纯水，如图1所示。

图1 中心探测器

建设方要求结构整体稳定系数大于2.5，并要求在长期工况下(对应探测器的正常运行状态)有机玻璃球的支撑杆轴心拉力小于90kN，轴心压力小于150kN。

本文采用有限元分析手段对结构的整体稳定性进行分析和评价。

2 结构体系

设计最终采用的结构体系为：有机玻璃球+单层四边形正交网格不锈钢网壳+赤道附近与不锈钢网壳相连的底部支承结构+支承有机玻璃球并与有机玻璃球表面垂直的590个撑杆，如图2所示。

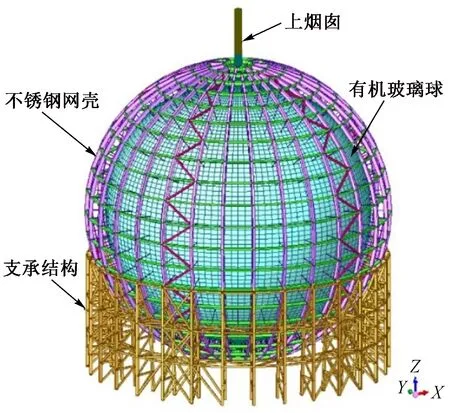
图2 中心探测器结构示意

有机玻璃球内径为35.4m，壁厚为120mm，由590个撑杆所支承，如图3所示。为了控制撑杆在运行工况下轴心拉力小于90kN，下半球第1～9层的220个撑杆(直径D=60mm)在不锈钢网壳一端采用碟形弹簧调整轴向刚度，并通过两组推力关节轴承实现撑杆在受拉时可以转动约5°，实现了与不锈钢网壳的弹性铰接连接，另一端与有机玻璃球铰接连接，如图4所示。其余撑杆(直径D=85mm)与不锈钢网壳刚接，与有机玻璃球铰接，为了便于安装，在安装阶段，撑杆与不锈钢网壳连接端可以通过推力关节轴承实现小角度的转动，便于适应安装误差，待撑杆就位后将节点锁定为刚接，如图5所示。

图3 中心探测器结构剖面图

图4 弹性铰接节点

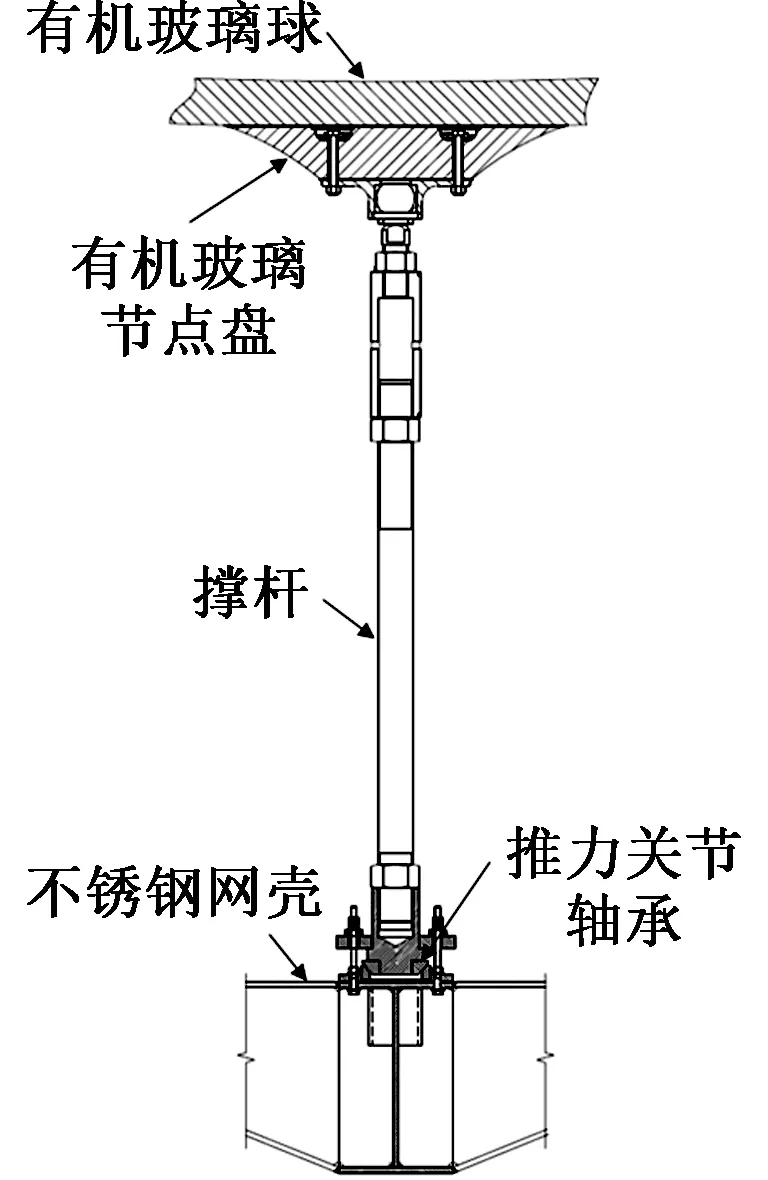
图5 刚性连接节点

3 结构稳定性问题及分析模型

3.1 结构稳定性问题

由于有机玻璃球内部灌装的液闪密度为860kg/m3，小于有机玻璃球外部水池中超纯水密度1 000 kg/m3，因此中心探测器主体结构受到巨大的浮力。整个结构及附属结构和设备的总重力约为2 135t，而结构所受的总浮力为5 154t，浮力远大于重力。而连接有机玻璃球与不锈钢网壳的590根撑杆是浮力从有机玻璃球传递至不锈钢网壳的荷载路径上的关键构件。在浮力作用下，位于上半球的撑杆受压力作用，位于下半球的撑杆受拉力作用。由于物理试验的要求，所有的撑杆均指向球心并与有机玻璃球表面垂直。

采用ABAQUS软件的buckle模块对施工图结构模型(简称模型M0)进行特征值屈曲分析，再将直径85mm的撑杆两端均设置为铰接的模型(简称模型M0a)进行特征值屈曲分析。两个模型的分析结果如表1所示，模型M0a第1，3阶屈曲模态如图6所示。

特征值屈曲分析结果对比 表1

图6 特征值屈曲分析失稳模态

由屈曲分析的结果可知，当所有撑杆两端均为铰接时，有机玻璃球与不锈钢网壳之间的连接实际为瞬变体系，有机玻璃球的抗旋转刚度很弱。有机玻璃球在向上的巨大浮力作用下，同时又受到一定的侧向力时，上半球的撑杆可能在水平面上绕顺时针或逆时针发生同步的偏转，同时有机玻璃绕Z轴旋转，有机玻璃球的抗浮刚度随之降低，有机玻璃球一边旋转一边上升，从而发生整体失稳，如图7所示。因此，必须加强有机玻璃球的抗旋转刚度，从而提高结构的整体稳定性。

图7 模型M0a在浮力作用下的结构失稳状态示意

在前期的方案比较中，考虑过在赤道位置设置大刚度的悬臂梁，或者设置向下的斜杆，如图8所示，两个方案均能大幅提高结构的整体稳定性，但是两个方案在运行工况下，在赤道处有机玻璃节点受到的剪力均超过了5kN的限值，因此予以放弃。最终采用的结构方案中，将370个未设置碟形弹簧的撑杆均设置为与不锈钢网壳刚接，与有机玻璃球铰接，在提高结构稳定性的同时，也将有机玻璃节点受到的剪力控制在5kN以内。

图8 悬臂梁方案和斜杆方案示意图

3.2 稳定性分析模型

本节采用ABAQUS软件的riks模块对结构的整体稳定性进行全面的考察。

3.2.1 材料属性

结构主要由不锈钢和有机玻璃两种材料组成，不锈钢材料为奥氏体型S30408[2]，分析中采用Gardner提出的两阶段本构模型[3]，密度7 900kg/m3，弹性模量193GPa，名义屈服强度f0.2=205N/mm2，抗拉极限强度fu=515MPa，泊松比0.3，线膨胀系数1.73×10-5/℃。有机玻璃材料的拉伸和压缩应力-应变曲线如图9所示，由于标准工况下有机玻璃应力控制在4.0MPa以内，处于弹性阶段，因此，稳定性分析中，有机玻璃采用弹性材料，密度1 180kg/m3，弹性模量3.277GPa，泊松比0.376，线膨胀系数7×10-5/℃。

图9 有机玻璃材料的拉伸和压缩应力-应变曲线

3.2.2 构件模型

不锈钢网壳和支承体系采用B32三节点梁单元模拟，有机玻璃球采用S4R壳单元模拟，两端铰接的撑杆采用T3D2杆单元模拟，一端铰接一端刚接的撑杆采用B32梁单元模拟。

3.2.3 初始缺陷

根据对比需要，每个分析模型中会考虑构件缺陷、有机玻璃球整体初始旋转、撑杆与有机玻璃球表面不垂直这三种初始缺陷中的1或2种情况。

(1)构件缺陷

根据《钢结构设计标准》(GB 50017—2017)[4]，不锈钢构件初始弯曲缺陷值取e0/l=1/300，利用B32三节点梁单元的中点偏移来实现。

(2)有机玻璃球整体初始旋转

根据特征值屈曲分析结果，对有机玻璃整体绕Z轴或Y轴旋转一定角度，如按照《空间网格结构技术规程》(JGJ 7—2010)[5]的规定，几何缺陷最大值为有机玻璃球直径的1/300，对应的旋转角度为0.4°。对比分析中考虑旋转角度绕Z轴旋转0.2°，0.4°，0.8°，1.2°，1.5°，绕Y轴旋转0.2°，0.4°，0.8°，1.2°，1.5°等不同情况。

(3)撑杆与有机玻璃球表面不垂直

考虑实际安装的撑杆与有机玻璃球表面不完全垂直，与节点处有机玻璃球表面的法向存在一个夹角，并且每个撑杆的角度以及偏转的方向都是随机的。对比分析中考虑撑杆随机偏转角标准差为0°，0.1°，0.2°，0.3°，0.4°，0.5°等六种情况。标准差为0.2°，0.5°的随机偏转角分布如图10所示。

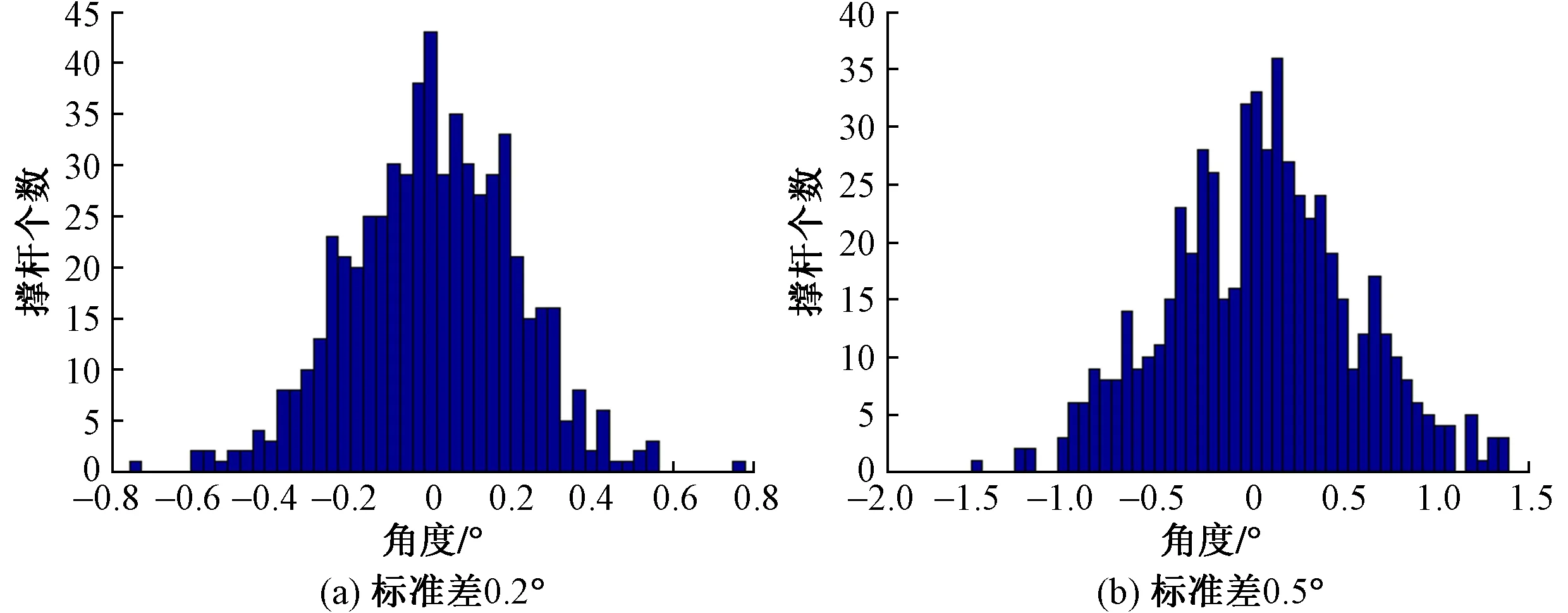
图10 随机偏转角分布

需要说明的是，为了控制计算量，分析中未考虑有机玻璃节点盘与有机玻璃球之间的接触问题，相应的内容可参考文献[6]和文献[7]中的有机玻璃节点精细化分析。

3.2.4 分析模型汇总

本文利用如表2所示的共37个考虑不同撑杆端部约束和初始缺陷的模型，对结构的稳定性进行研究，分析影响结构稳定性的因素，并评估施工图设计模型的稳定性。各模型均考虑构件初始弯曲缺陷。

结构稳定性分析模型编号及说明 表2

3.2.5 稳定性评价标准的确定

结构整体的失稳状态是有机玻璃球旋转，但是旋转的方向不确定，出现最大位移的节点不确定，因此常用的节点位移-荷载曲线很难确定极值点(结构失稳前的最大荷载)。本文针对结构的特点，采用上半球280个受压撑杆的内力平均值F来评价结构的稳定性，当F随着荷载系数K的增加而减小时，认为结构开始失稳。并认为在K值相同时，F-K曲线的斜率越大，结构的稳定性越好。

4 稳定性计算结果及分析

4.1 撑杆两端约束状态的对比

图11为模型M0，M1_2，M2_2，M0a，M1_2a，M2_2a的F-K曲线，稳定系数分别为3.45，3.28，4.25，6.23，3.03，1.82。从F-K曲线的斜率看，模型M0，M1_2，M2_2的稳定性均优于模型M0a，M1_2a，M2_2a。而从稳定系数看，上半球撑杆与不锈钢网壳刚接的模型M0，M1_2，M2_2稳定系数均大于3.0，而所有撑杆两端均铰接的模型M0a，M1_2a，M2_2a的稳定系数离散性大，特别是M2_2a在稳定系数为1.82时，有机玻璃球绕斜轴发生旋转开始失稳，失稳模态如图12所示，未满足设计要求。可见上半球撑杆与不锈钢网壳刚接后，结构的稳定性有较大提高，在有机玻璃球整体绕Z轴或水平Y轴旋转0.4°的情况下，稳定系数仍然超过3。而所有撑杆两端均铰接的模型，当存在较大的整体缺陷时存在旋转失稳风险。

图11 模型M0，M1_2，M2_2，M0a，M1_2a，M2_2a的F-K曲线

图12 模型M2_2a失稳模态

4.2 撑杆外端部约束状态的影响

撑杆外端部即撑杆与不锈钢相连位置。图13给出了模型M1_2，M2_2a，M2_2b，M2_2c，M2_2d的F-K曲线，稳定系数分别为3.20，3.13，3.14，3.17，3.13。结合F-K曲线的斜率，可以看出，刚接撑杆数目的增多能有效提高有机玻璃球的转动刚度，370个不带碟形弹簧的撑杆的外端部均为刚接时，结构刚度最大，稳定性最好；同时，相比于约束顶部的撑杆，约束靠近赤道的撑杆对提高结构的稳定性更为有效。

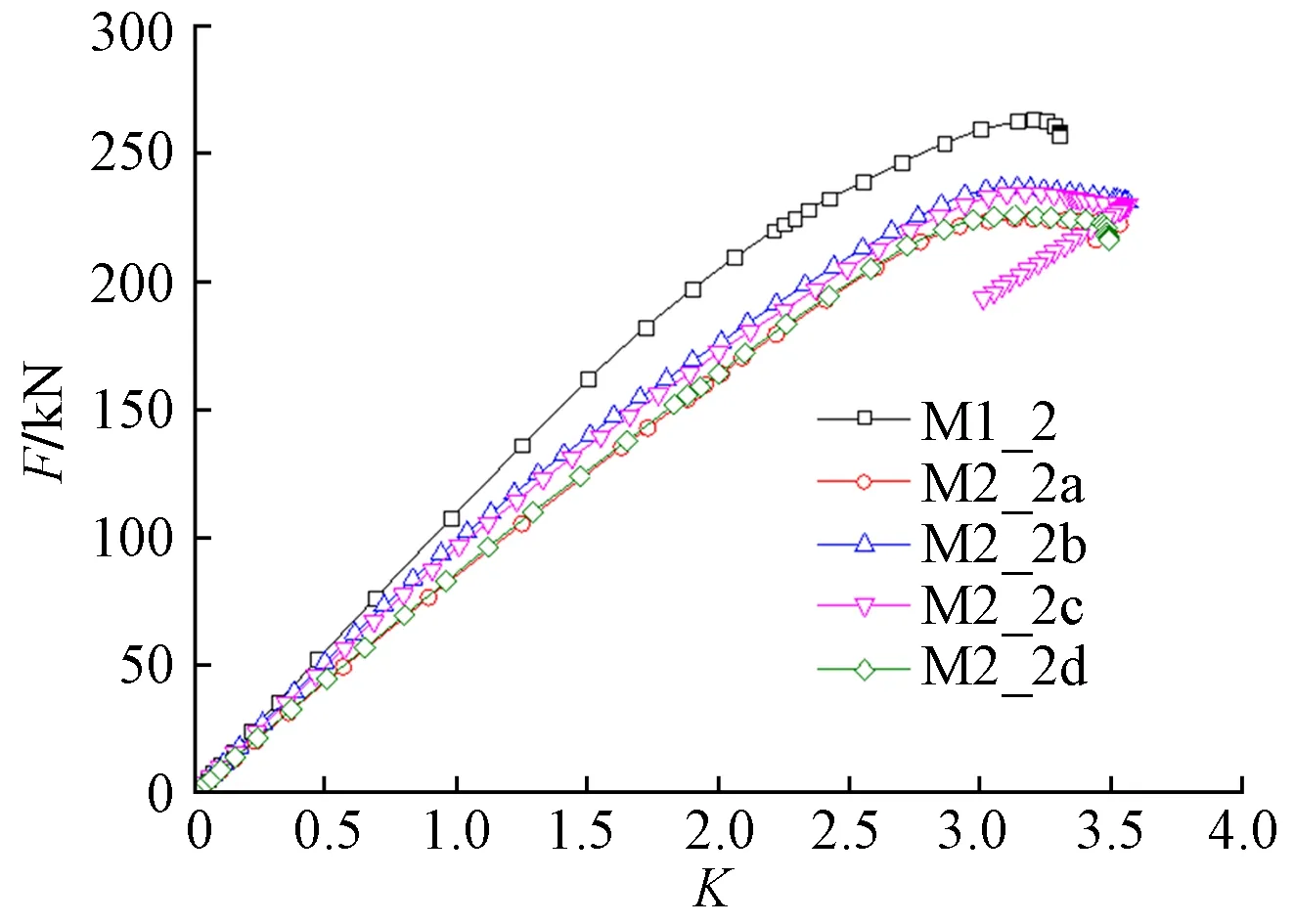
图13 模型M1_2，M2_2a～d的F-K曲线

4.3 有机玻璃球初始旋转的影响

由图14和图15可知，随着有机玻璃球整体旋转角度的增加，结构整体稳定性逐渐降低，但是降低幅度不大。由于受到浮力的影响，相比于绕Y轴旋转，绕Z轴旋转时结构稳定性降低更加明显。

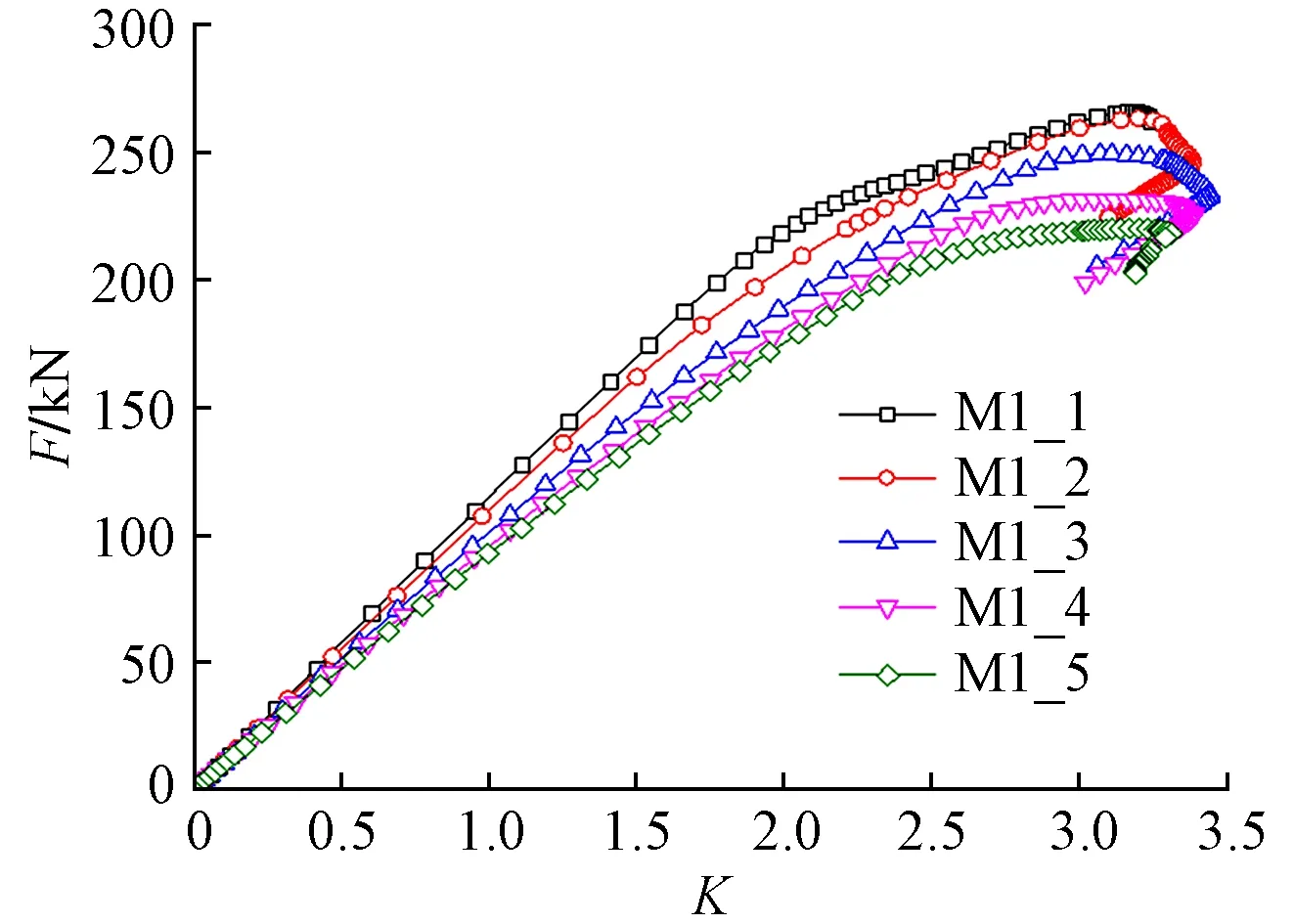
图14 模型M1_1～5的F-K曲线

图15 模型M2_1～5的F-K曲线

4.4 随机偏转角的影响

对比图16和图17可知，370个不带碟形弹簧的撑杆的外端部均为刚接的模型M0,M0_R0.1～0.5d，随着撑杆随机偏转角标准差的增加，稳定性有所降低，但是降低幅度不大，且分析的6个模型稳定系数均大于3.2，在K小于3时，各模型的F-K曲线相互重叠。而590个撑杆两端均铰接的模型M0a_R0.1～0.5d，不同的偏转角标准差下，稳定性系数有高有低，模型M0a_R0.3d的稳定性系数仅为1.72，进一步说明了所有撑杆两端均铰接的模型当存在较大的初始缺陷时存在提前失稳的风险。

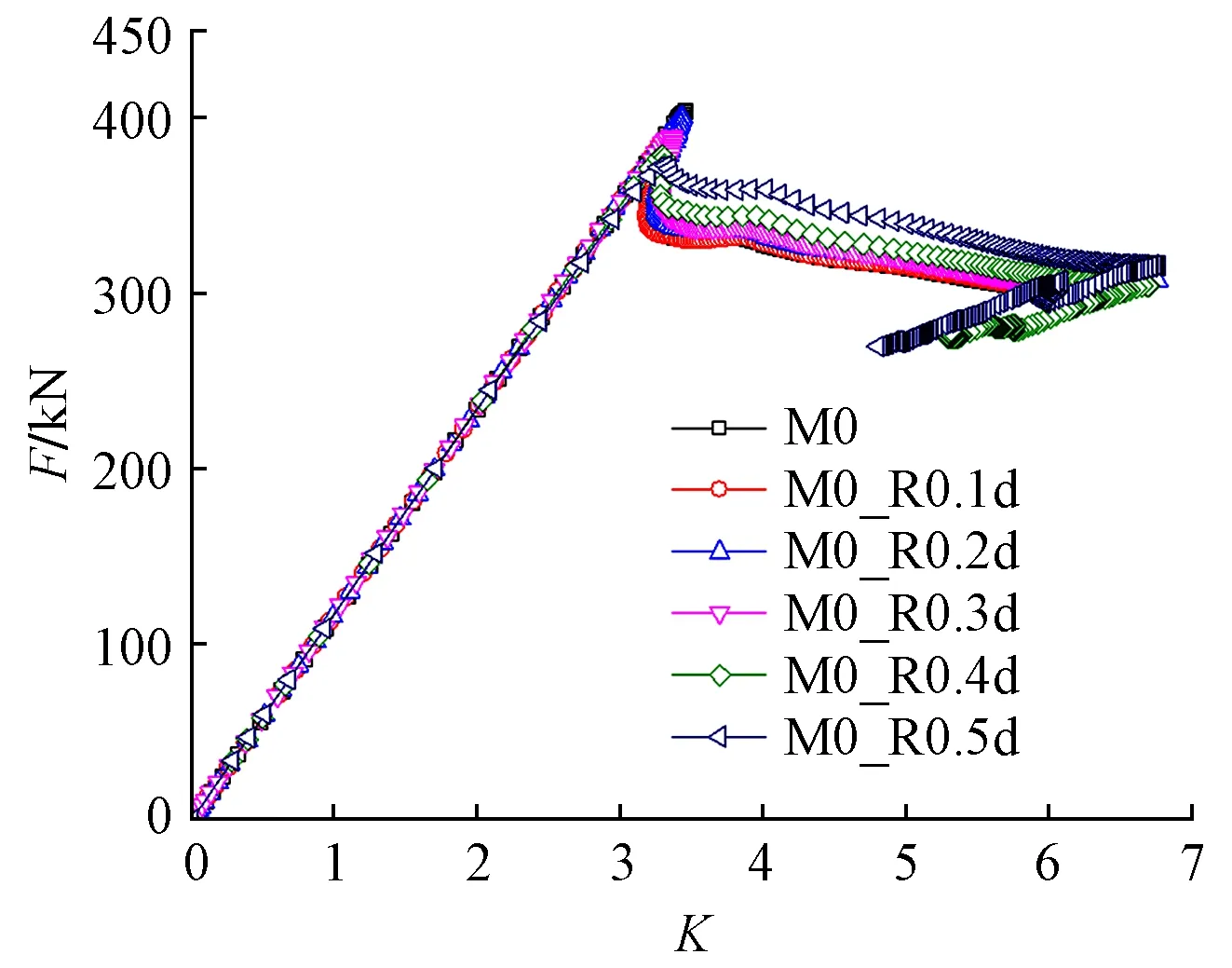
图16 模型M0,M0_R0.1～0.5d的F-K曲线

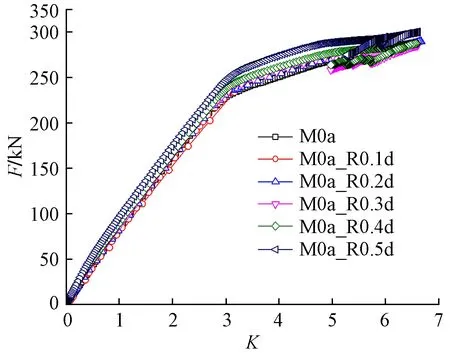
图17 模型M0a,M0a_R0.1～0.5d的F-K曲线

4.5 不同随机变量的影响

模型M0_R0.2d_1～10是在模型M0基础上，采用标准差均为0.2°的10套不同随机偏转角对590个撑杆进行随机偏转的10个模型。从图18可知，10个模型的F-K曲线基本重合，稳定性基本一致。说明标准差相同时，不同的随机偏转角对结构稳定性的影响很小。10个模型的稳定系数分别为3.43，3.29，3.42，3.34，3.30，3.28，3.41，3.36，3.31，3.31，平均稳定系数为3.35。

图18 模型M0_R0.2d_1～10的F-K曲线

根据模型M0_R0.2d_1的分析结果，见图19和图20，当荷载系数K从3.43降为3.42时，下半球第10层撑杆率先进入屈服，同时有机玻璃球相对不锈钢网壳出现旋转的趋势，随后屈服的撑杆数量逐渐增加，受压撑杆的平均压力从401kN降低为345kN，有机玻璃球收到的浮力逐渐往下半球的受拉撑杆转移，随后，受压撑杆平均压力缓缓降低，荷载系数逐步增加，尚有很大的上升空间，说明结构部分构件进入屈服后，还具备良好的承载能力。

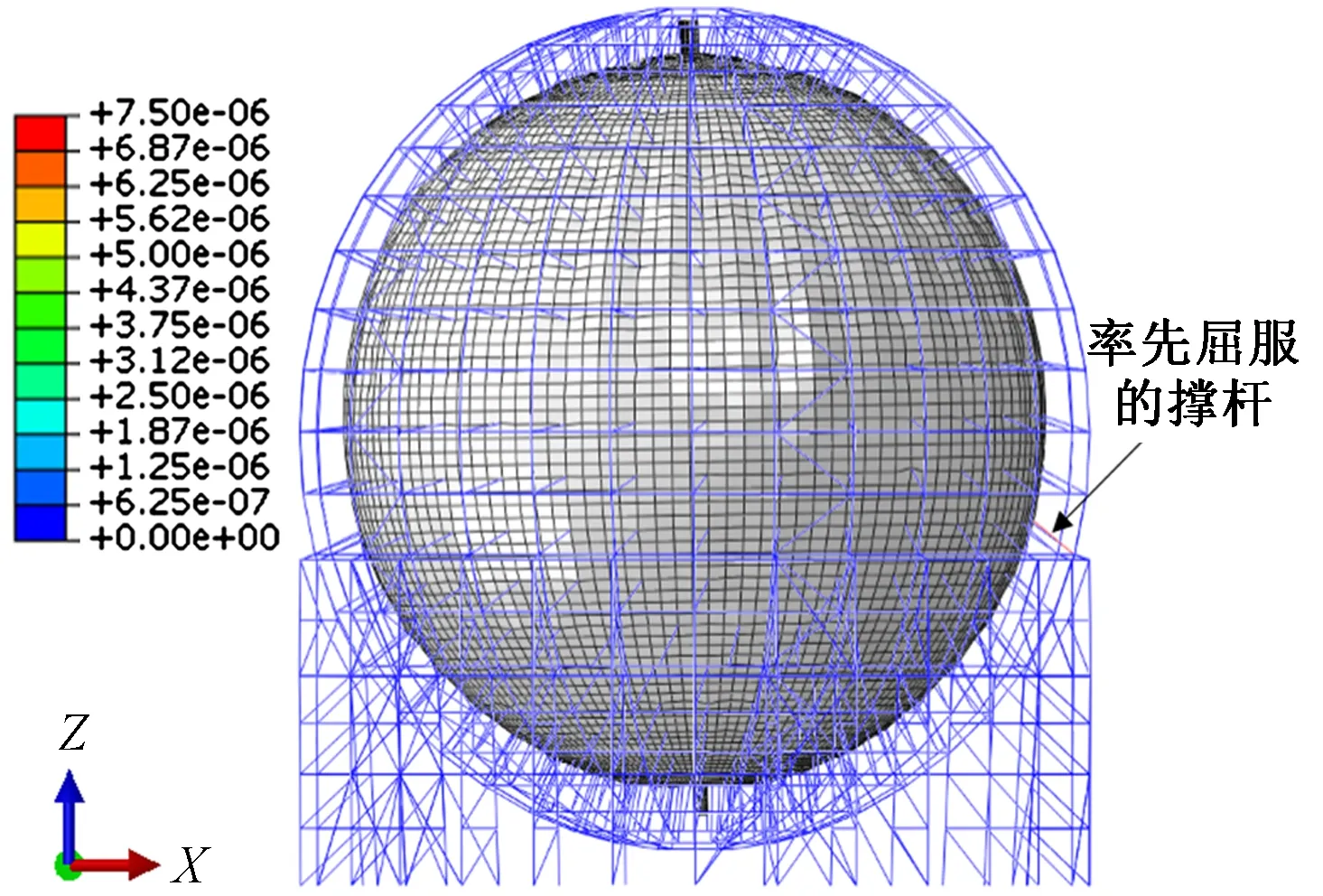
图19 模型M0_R0.2d_1荷载系数K=3.42时应变分布

图20 模型M0_R0.2d_1荷载系数K=3.42时位移分布

5 结论

本文首先介绍了JUNO中心探测器主体不锈钢结构的结构体系，阐述了结构在巨大浮力作用下的稳定性问题及失稳模式，针对结构的特点，提出了结构整体稳定性评价标准。通过对一系列模型的稳定性分析和对比分析得出如下结论：

(1)结构主要的失稳形式是在浮力作用下的有机玻璃球整体旋转上升。

(2)与不锈钢网壳刚接的撑杆数目的增多能显著提高有机玻璃球的转动稳定性；相比于约束顶部的撑杆，约束靠近赤道的撑杆对提高结构的稳定性更为有效。所有撑杆两端均铰接的模型，当存在较大的整体缺陷时存在提前失稳的风险。施工图方案的370个不带碟形弹簧的撑杆的外端部均为刚接是最优的选择。

(3)有机玻璃球的初始整体旋转对结构整体稳定性有一定削弱。

(4)施工图模型随着撑杆随机偏转角标准差的增加，稳定性有所降低，但降低幅度不大。而590个撑杆两端均铰接的模型在不同的偏转角标准差下，稳定性系数有高有低，最低的仅为1.72，存在提前失稳的风险。

(5)根据采用标准差均为0.2°的10套不同随机数对590个撑杆进行随机偏转的10个模型的稳定性分析结果，结构考虑初始缺陷的双非线性稳定性系数可取3.35，满足设计要求。