基于B氏距离准则的图案几何纹样提取仿真
周 峰,班 倩
(湖北工业大学,湖北 武汉 430068)
1 引言
图案中的几何纹样具有强大的视觉冲击力、丰富的文化底蕴和规律性,所以几何纹样被广泛应用于服装设计、室内设计、家居造型设计等各种现代设计中[1],目前越来越多的设计者将几何纹样图案应用于各领域设计中,并不断发展以及创新,使几何纹样有了进一步发展,几何纹样的不断发展推动人类对于传统文化的深入研究[2]。为便于人类研究图案几何纹样,使图案几何纹样应用于更多领域中,众多研究学者对几何纹样的特征提取作出研究。
文献[3]提出基于形态学的图案几何纹样提取技术。将模糊函数变换到极坐标域,提取图案均面积和致密度作为特征向量,通过模糊C均值聚类完成特征提取。该方法时滞性较好,但提取精度较差;文献[4]提出基于小波包分解的图案几何纹样提取技术,对图案进行3层小波包分解,重构节点,提取重构信号峰值,计算特征平均欧氏距离,其最小值对应的节点即为最优小波包节点,从中提取特征点,完成纹样提取。该方法提取耗时较短,但是效果不太理想。
针对上述方法存在的问题,研究基于Bhattacharyya(简称B氏)距离准则的图案几何纹样提取仿真,利用B氏距离准则算法有效提取图案中的几何纹样,B氏距离准则算法是特征提取中较为有效的方法,该方法利用核函数将测试样本非线性映射至高维核空间,并在高维核空间中寻找最优特征向量,将最优特征向量样本映射至低维特征空间后,精确提取图案中的几何纹样特征。
2 图案几何纹样提取
2.1 图案几何纹样特征
形状文法是常用的几何纹样设计方法,形状文法是利用不同形状获取形状衍生形态的图案图形设计方法[5],形状文法已经被广泛应用于服装设计、室内设计等众多图案设计领域。
形状文法是依据固定规则旋转、移动或镜像几何形状获取所需图案的方法[6],经过形状文法获取的图案可保留原有几何形状特征,且丰富图案内容。
几何纹样在不同图案中可呈现不同特色,具有灵活的特点,几何纹样在图案中可单独呈现,也可以重复和连续的状态呈现,利用不同的几何纹样可组成不同形态的图案[7]。目前应用于图案中的几何纹样众多,本文仅总结典型图案中常见的几何纹样,常应用于图案中的几何纹样特征如表1所示。

表1 常见的几何纹样特征
表1为常应用于现代设计典型图案中常见的几何纹样特征,通过表1可以看出,几何纹样通常由线或菱形、圆形、长方形等几何图形组成[8],由点、线或不同几何形状构成了常应用于图案设计中的几何纹样。
2.2 基于Bhattacharyya距离准则的图案几何纹样提取
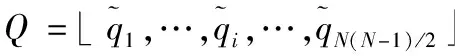
模式分类中,为使分类精度与原始空间需要的最小特征空间维数为本征维;分类判决面与其中某一点垂直的特征向量称为分类有效特征向量。
图案几何纹样核空间提取矩阵如下
∑B=QQT
(1)
式中,QT为图案特征向量转置矩阵。核空间维数一般较高,甚至可能达到无穷[10],用H表示核空间维数,可得H×H矩阵为ΣB,提取问题的本征维以及提取特征向量有效性受ΣB影响。
ΣB的秩可作为模式分类问题的本征维,分类有效特征向量是与ΣB的非零特征值相对应的特征向量。
设ΣB的正交特征向量为
rank(ΣB)=T,{η1,η2,…,ηT}
(2)
式中,T为转置向量,ηT为正交向量。通过不同类别的最优线性分类面确定多类特征分类问题与核空间的分类判决[11],因此垂直于判决面点的随机矢量V⊥公式如下
(3)
扩展{η1,η2,…,ηT}可得正交基{η1,η2,…,ηT,ηT+1,…,ηH},且〈ηi,ηj〉=0,i≠j,因此可知V⊥和{ηT+1,…,ηH}正交,原因如下

(4)
以上公式需满足T+1≤i≤H。
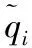
矩阵ΣB存在于核空间中,过高的维数将导致无法直接获取特征值以及特征向量[12],利用核函数提取核空间特征。
K=〈Q,Q〉=QTQ
(5)
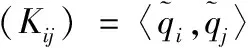
(6)
以上公式需满足1≤i,j≤N(N-1)/2,(K)lh=〈zl,zh〉。
ΣB与K均为正定对称阵,可得奇异值分解结果如下
ΣB=D·K
(7)
K=ΓT·Λ·Γ
(8)
以上公式中,D与Λ均为对角阵。
分类有效特征向量为存在于对角阵D对角线中的非零元素相对应U的列向量。式(7)与式(8)的关系公式如下
(9)
U=Λ-1/2·Γ·QT
HPLC-CAD法同时测定风湿定片中7种活性成分的含量…………………………………………………… 侯爱荣等(23):3212
(10)
设存在新样本x∈Td,特征向量为U的列向量时,所提取特征公式如下
F=〈U,Ψ(x)〉=Λ-1/2·Γ
(11)
设非零元素存在与对角阵D对角线数量为M,用{li}表示非零元素的列标号,且满足1≤i≤M,可得B氏距离准则算法提取分类有效特征公式如下
FB={Fj},j∈{li}
(12)
式(12)中,Fj为所提取分类有效特征的第j个元素。
依据式(9)和式(10)可知,rank(K)=rank(ΣB),因此可知,特征模式分类问题中,核矩阵K的秩与本征维相同。
通过以上分析过程可知,采用B氏距离准则方法提取图案几何纹样过程如下:
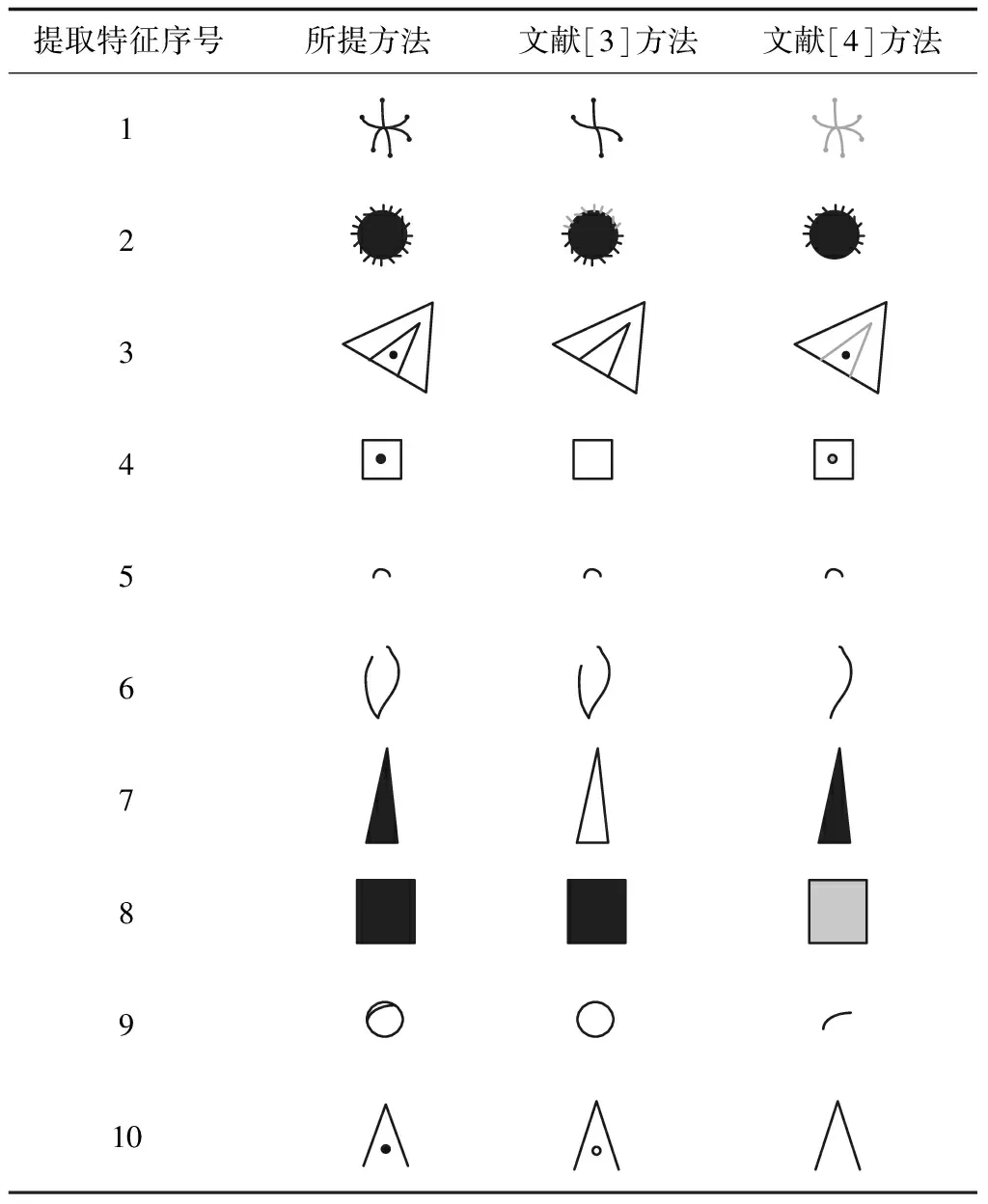
1)获取图案中几何纹样与其它纹样的局部最优特征向量qij,需满足1≤i 2)利用式(5)获取核矩阵; 3)分解矩阵使分解后结果以式(8)形式呈现,通过式(11)提取图案几何纹样特征,可得FB为采用B氏距离准则方法提取的几何纹样有效特征。 为验证本文研究基于B氏距离准则的图案几何纹样提取有效性,设计实验。选用Matlab仿真软件为实验平台,利用Turbo C++3.0开发软件编程,检测所提方法的提取效果,并采用文献[3]方法、文献[4]方法为实验对比方法。 在Visual Genome 图像库(http:∥dataju.cn/Dataju/web/datasetInstanceDetail/85)中选择具有大量几何纹样特征的图案,如图1所示。 图1 具有大量几何纹样特征的图案 图1为采用大量几何纹样绘制的图案,该图像图案中具有鲜明的几何纹样特征,其中包括圆形、三角形、正方形等大量几何纹样,因此极具有研究意义。 采用三种方法分别提取该图像中图案几何纹样,不同方法提取图1图案中几何纹样对比结果如表2所示。 表2 不同方法提取几何纹样结果对比 通过表2不同方法提取图案几何纹样的对比结果可以看出,采用三种方法均可有效提取图1图案中的几何纹样,但所提方法提取的几何纹样完整度较高,所提取图案几何纹样结果与构成图案的几何纹样一致,并且具有较高的清晰度;而采用文献[3]方法以及文献[4]方法虽然可以有效提取图案中的几何纹样,但所提取几何图样完整度较低,并且部分实心图案无法有效提取。所提方法可准确提取几何纹样的颜色特征,而另两种方法均出现无法提取图案几何纹样颜色以及所提取图案几何纹样颜色错误情况。通过表2几何纹样提取对比结果能够得出所提方法可有效提取图案几何纹样特征,且提取到几何纹样的清晰度较好。 为进一步验证所提方法提取有效性,另选取具有不同数量几何纹样且几何纹样特征较为鲜明的十幅图案,检测三种方法的图案几何纹样提取效果,图案几何纹样提取对比结果如表3所示。 表3 不同图案几何纹样提取结果 表3实验结果可以看出,所提方法准确提取图案几何纹样数量高于另两种方法,其它两种方法存在较多的多提取问题。计算得出所提方法提取10幅图案几何纹样,提取精度均在97%以上,而采用小波包分解方法以及形态方法提取提取10幅图案中几何纹样,提取精度最低仅为91.7%和94.4%,所提方法提取10幅图案几何纹样提取精度明显高于小波包分解方法以及形态方法,验证所提方法对图案几何纹样的提取精度。 统计三种方法提取图案中几何纹样所需时间如图2所示。 图2 不同方法提取时间对比 通过图2图案几何纹样提取时间对比结果可以看出,所提方法提取10幅图案中几何纹样时间均低于30ms;而文献[3]方法与文献[4]方法方法提取10幅图案几何纹样的最短时间为50ms和53ms,所提方法可在较短时间内有效提取图案几何纹样,验证所提方法具有较高的提取效率。 图案中通常具有不同程度的干扰噪声,干扰噪声对图案几何纹样提取结果影响极大,统计在图案中加入30dB干扰噪声时三种方法提取图案几何纹样的提取结果,验证所提方法提取图案几何纹样的抗干扰性能,对比结果如表4所示。 表4 30dB干扰噪声下提取结果对比 通过表4实验结果可以看出,在加入30dB干扰噪声情况下,所提方法提取图案几何纹样的提取精度有所下降,提取时间有所提升,但是与文献方法对比,所提方法提取精度以及提取时间仍高于另两种方法。所提方法提取10幅图案的几何纹样提取平均时间仅为64.5ms,提取精度高达98.1%;而文献[3]方法提取图案几何纹样的平均提取精度仅为93.6%,平均提取时间高达113.7ms;文献[4]方法提取图案几何纹样的平均提取精度仅为95.1%,平均提取时间高达134.6ms。分析实验结果可知,所提方法不仅具有较高的图案几何纹样提取性能,可快速提取图案几何纹样,且在图案存在噪声干扰情况下,仍可保持较高的提取精度以及较优的提取性能,说明所提方法具有较高的提取稳健性。 为呈现图案几何纹样的美观性,设计师需要具有更高的色彩搭配以及美学设计技术,提取图案几何纹样,对于图像研究以及室内设计、服装设计等众多领域中具有较高的意义。本文先分析常见的图案几何纹样特征,利用基于Bhattacharyya距离准则算法有效提取图案的几何纹样,为验证该方法有效性,在Matlab仿真平台中通过大量实验验证提取有效性,实验结果表明,采用该算法不仅具有较高的提取精度以及提取效率,且受噪声干扰影响较低,是一种有效的图案几何纹样提取方法。利用图案几何纹样提取方法研究几何纹样的美学价值,对于几何纹样应用于众多领域中的设计具有重要意义。3 实验分析

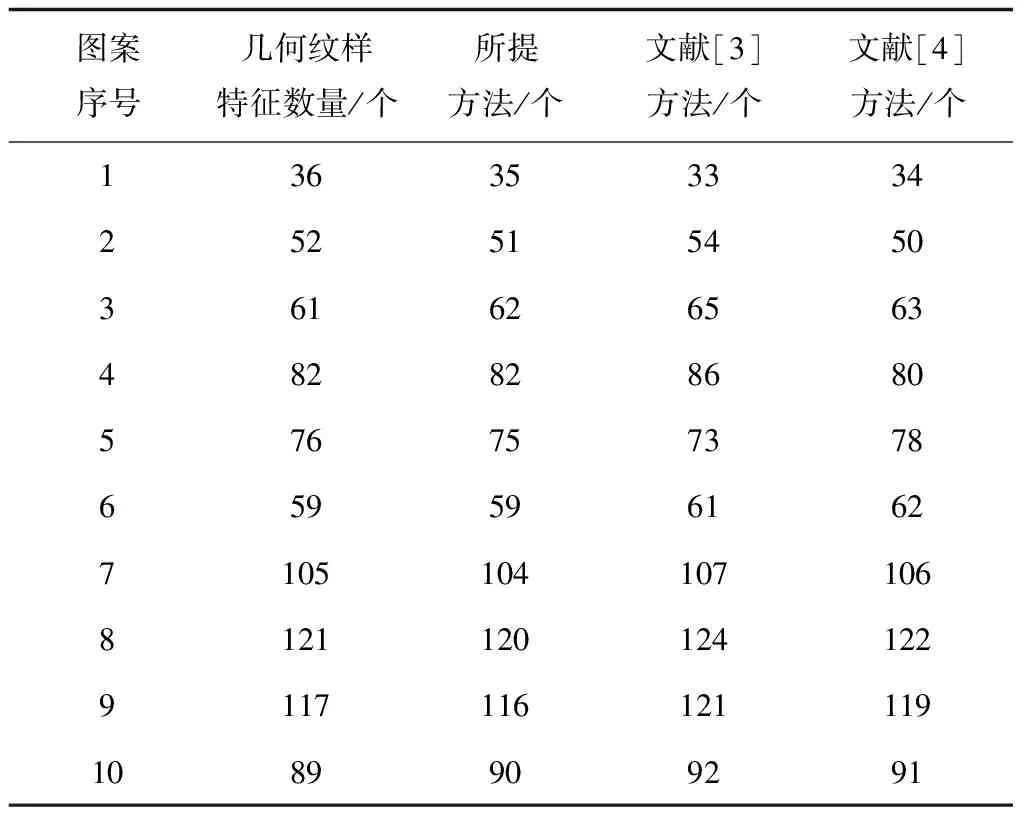
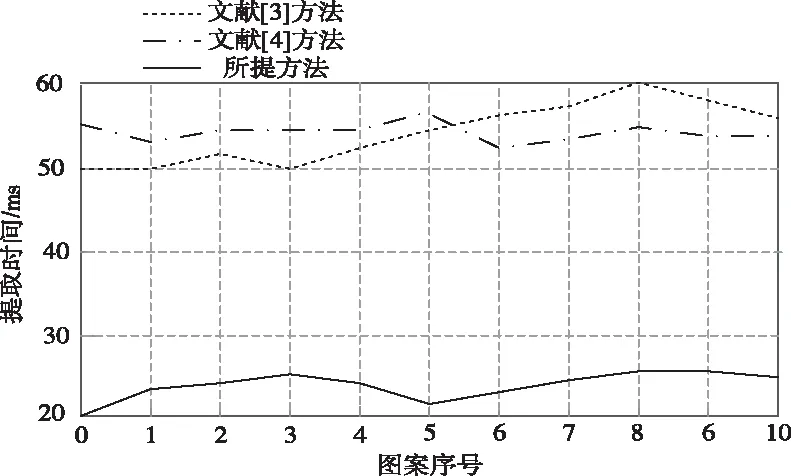
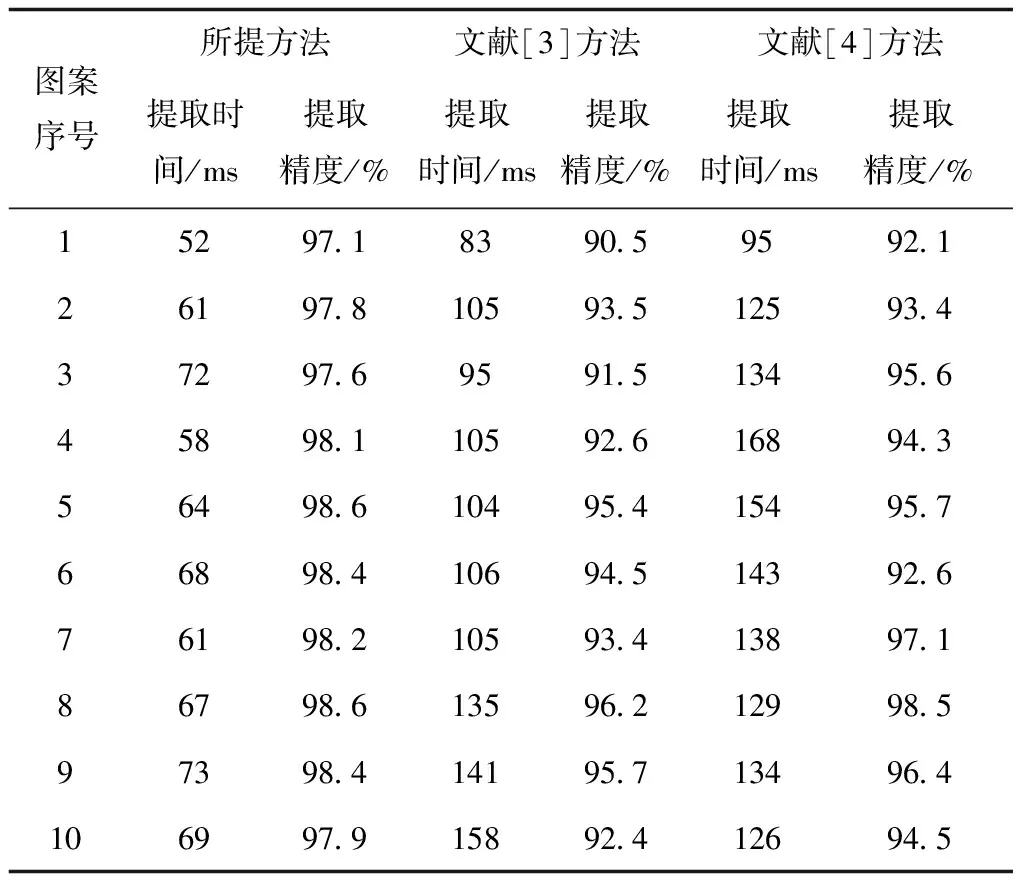
4 结论

