一种高效的双边聚类集成算法

杨 辉，彭 晗，朱建勇，聂飞平

(1.华东交通大学电气与自动化工程学院，江西 南昌 330013；2.江西省先进控制与优化重点实验室，江西 南昌330013；3.西北工业大学光学影像分析与学习中心，陕西 西安710072)

1 引言

在数据挖掘，机器学习等领域中，聚类技术是无监督数据探索和分析的重要工具，但数据聚类仍然是一个非常具有挑战性的问题。其目的是发现给定数据集本身的固有结构并将该数据集划分为特定的同类组，即簇。在过去的几十年中，通过利用各种技术提出了许多聚类算法[1-6]。

聚类集成旨在合并多个聚类[7]以获得可能更好，更鲁棒的聚类结果，这在发现奇异聚类，处理噪声的聚类解决方案方面显示出优势[8]。随着聚类集成技术的不断发展，其中有些研究者通过结合其它技术来提高最终聚类准确率，如投票法[9]、超图划分[10]。Fred等[11]提出了证据累积方法，通过断裂最弱的连接发现自然的簇。王红军等[12]提出了一种基于隐含变量的聚类集成模型，直接利用多个聚类的结果来组成原始数据集的不同特征，直接应用聚类算法。Strehl等[13]基于图划分的思想提出了基于簇相似的分割算法CSPA(Cluster-based Similarity Partitioning Algorithm)，超图分割算法HGPA(HyperGraphs Partitioning Algorithm)和元聚类算法MCLA(Meta-CLustering Algorithm)3种聚类集成算法。通过构造共协矩阵，并将样本和基聚类分别作为图的顶点，将最初的优化问题转化为图的分割问题，有效提高了聚类质量。Fern等[14]提出一个称为混合二部图的构想HBGF(Hybrid Bipartite Graph Formulation)算法充分的利用样本与基聚类之间的潜在信息。

以往的聚类集成不能直接得到最终的聚类结果，得到的解还需要运用传统的聚类算法比如k-means算法[15]，谱聚类算法[16]等等，在整个过程中使解由离散-连续-离散的转变，可能会导致最终的解与最优解产生较大的偏离。本文提出的聚类集成SBKM(Spectral Bilateral K-means Algorithm)不仅准确度高而且可以直接得到最终的聚类结果。在生成基聚类阶段运用谱聚类算法得到多个的基聚类。在多个基聚类中，用NMI(Normalized Mutual Information)聚类评价指标选取基聚类，通过增大聚类结果中基聚类之间的差异，从而获得更好的集成，并将选出的基聚类结果作为新矩阵的特征并转换为对应的指示矩阵，将新的矩阵作为输入通过双边聚类算法BKM(Bilateral K-means Algorithm)[17]将样本和基聚类同时聚类，直接得到最终的聚类结果。

为了更好的理解本文符号和规范的定义，总结如表1所示。

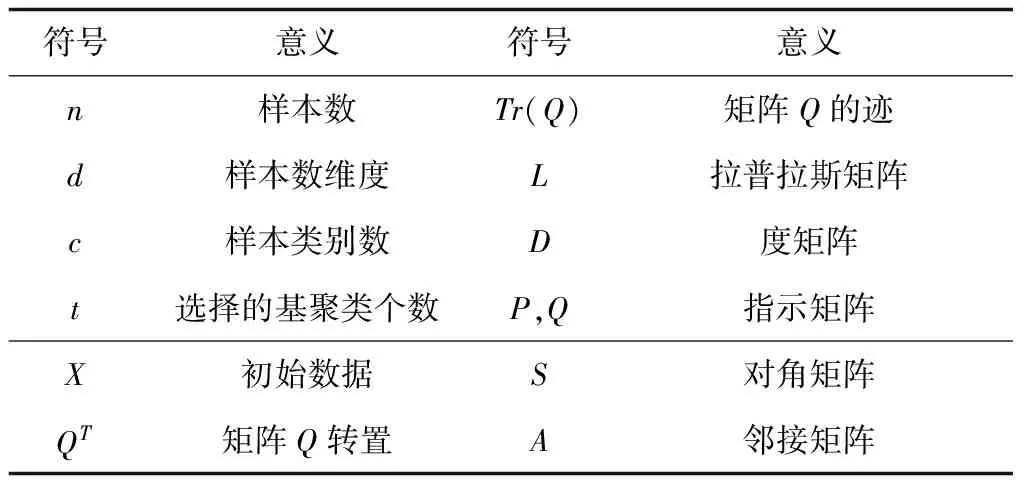
表1 符号的定义

2 谱聚类生成基聚类

谱聚类(spectral clustering)是一种基于图划分的方法，它通过构建图将聚类问题转变成图论里面的划分问题。在聚类里面应用比较广泛的的谱聚类算法Ncut(Normalized cut)，其目标函数可以表示为[18]

(1)

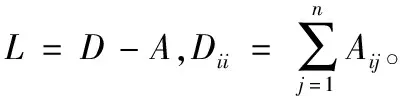
假定数据类别数为c，对初始数据运行m次谱聚类算法(Ncut)，得到m个聚类结果。从m个聚类结果中利用标准互信息NMI 选择基聚类。标准互信息计算公式[19]如下所示

(2)

式中nij表示聚类结果的第i个簇中包含原数据集类标签为j的样本总数，ni表示聚类结果的第i个簇的样本总数，nj表示原数据集类标签为j的样本总数，n表示样本总数。I和J分别表示聚类得到的簇个数和原数据集的类个数，如果NMI的值越接近1，说明和∂吻合程度越高，即所包含的信息越相似差异性较小。通过利用NMI评价指标从生成的m个聚类结果中来选择基聚类，从而增大基聚类之间的差异[20]。将最终得到的基聚类作为特征构建矩阵R=[r1，r2，…，rm]∈Rn×m，其中ri表示运行第i次谱聚类算法产生的基聚类的结果。通过计算基聚类ri与其它基聚类rj(i≠j)标准互信息总和，从而得到第i个基聚类总的平均标准互信息Ui，公式如下

(3)

Ui的值越大，说明第i基聚类里面所包含的信息与其它基聚类所包含的信息相差不大，从而使整体的差异性有所下降。在所有的基聚类中选出Ui中最小的t个基聚类，将t个基聚类分别转化为指示矩阵(每一行有且只有一个非零元素1，其它则为0)并将其作为新数据矩阵的特征(列)，即新的数据矩阵W∈Rn×(t×c)。例如通过选择最终有2个基聚类结果被选出来且数据簇数为2，分别为[1，1]T，[1，2]T。将其转化为指示矩阵[10;10]和[10;01]并作为新的数据矩阵W的特征(列)，即此时数据矩阵为[1010;1001]。

3 双边聚类一致性集成

将数据矩阵W的行和列同时作为图中的顶点，其邻接矩阵A可以表示为如下图所示

(4)

将多划分Ncut算法对所构图进行划分，在这个过程中双边聚类算法能将输入数据的行和列同时聚类。目标函数如下所示

s.t.Y∈φ(n+d)×c

(5)

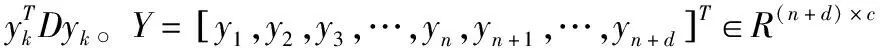
s.t.Y∈φ(n+d)×c

(6)

上式L=D-A，Y=[PT，QT]。所以式(6)可以改写为

(7)

即目标优化函数又可以转变成如下所示

(8)

由于上式求解是一个NP问题，加入Tr(WTW))和Tr((YTDY)-1PTP(YTDY)-1QTQ)，式(8)的目标优化函数可以转变成如下

(9)

式中P=[p1，p2，…，pn]T∈Rn×c矩阵里面保存着行(样本)的聚类结果，每一行有且只有一个非零元素1(若第i个样本属于第j个簇，则pij=1，其它则为0)，Q=[q1，q2，…，qd]T∈R(t×c)×c矩阵里面保存着列(特征)的聚类结果，每一行有且只有一个非零元素1(若第i特征属于第j个簇，则qij=1，其它则为0)。c为行和列的聚类簇数，S=(YTDY)-1为对角矩阵。通过交替更新的方法得到最终的最优值，更新如下

固定P，Q更新S，将目标函数展开并将其定义为J即

=Tr(WTW)-2Tr(QTWTPS)+Tr(SPTPQTQS)

(10)

对S求偏导，并令等式为零，即

(11)

由式(11)得S=[(PTPQTQ)T]-1(PTWQ)

在P，Q更新求解过程中将数据矩阵W分解即：在求解Q矩阵的过程中将数据矩阵W分解成t×c列，而在求解P矩阵的过程中则是将数据矩阵W分解成n行。

当固定S，P更新Q。目标函数可以表示为

(12)

(13)

式中R=PS，r·k代表矩阵R的第k列。在矩阵Q的寻优过程中。即寻找矩阵W分解后的每一列，与矩阵PSQT对应列的最小欧式距离，从而使得目标函数达到最小。由于Q为指示矩阵，其中每一行有且只有一个非零元素1。通过矩阵QT的第i列非零元素，选出矩阵R=PS中的第k列，使得r·k与矩阵W中的第i列的欧式距离达到最小值，从而使得目标函数达到最小值。

固定S，Q更新P。其目标函数可以表示为

(14)

(15)

式中L=SQT，lk·代表矩阵L的第k行。在矩阵P的优化过程中。即寻找矩阵W分解后的每一行，与矩阵PSQT对应行的最小欧式距离，从而使得目标函数达到最小。由于矩阵P中每一行有且只有一个非零元素1。在矩阵P第i行非零元素，选出矩阵L=SQT中的第k行，使得lk·与矩阵W中第i行的欧式距离达到最小值，使得目标函数达到最小值。即在更新每一个参数的过程中都会使得目标函数最小化，最终使得S，Q，P的值稳定不变时整个目标函数达到最小值，即目标函数收敛。

4 算法步骤

假定样本矩阵X∈Rn×d，样本的聚类簇数c，其步骤总结如下：

1)运行m次谱聚类算法，得到m个基聚类；

2)通过计算每个基聚类的平均标准互信息来选取基聚类，将选出的基聚类将基聚类转化为指示矩阵W；

3)根据式(11)、(13)、(15)分别计算S、Q、P；

4)最终收敛时指示矩阵P所存储的结果就是最终聚类结果。

5 实验结果与分析

本节将提出的聚类集成算法(SBKM)与流行的聚类集成算法相比较，并对所得的实验结果进行分析。并选取了标准互信息作为评价指标。

5.1 数据集

实验共选择7个数据集进行实验，这7个数据集都是来自数据库的真实数据。Ecoli，Yeast，Ionosphere，Solar，Auto和Zoo都是来自UCI的数据集，其中Ecoli和Yeast都是关于蛋白质的数据集，Ionosphere是雷达从电离层返回的分类数据集，Zoo 关于动物分类数据集，Dig1-10是来自benchmark的数字数据集。实验数据集的具体描述见表2。

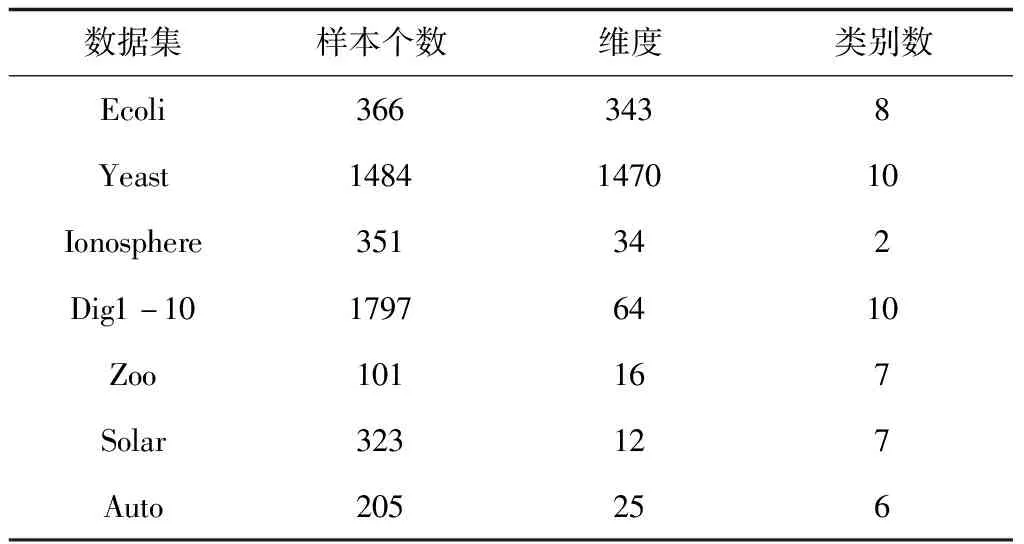
表2 数据集的具体描述

5.2 实验比较

在实验中，主要分为两个部分：第一部分，选取数据集(Ecoli，Yeast，Ionosphere，Dig1-10)作为数据输入分别独立运行多次谱聚类(Ncut)，选择出t个基聚类分别为20，30，40(即ensemble size分别为20，30，40)。独立运行SBKM聚类集成算法20次，记录每一次集成算法的最终聚类结果与真实标签的标准互信息，最终取20次标准互信息的平均值。并与4个聚类集成算法HGPA，MCLA，CSPA，HBGF 相比较，记录每次实验的标准互信息并求20次的平均值，实验结果如表3所示。

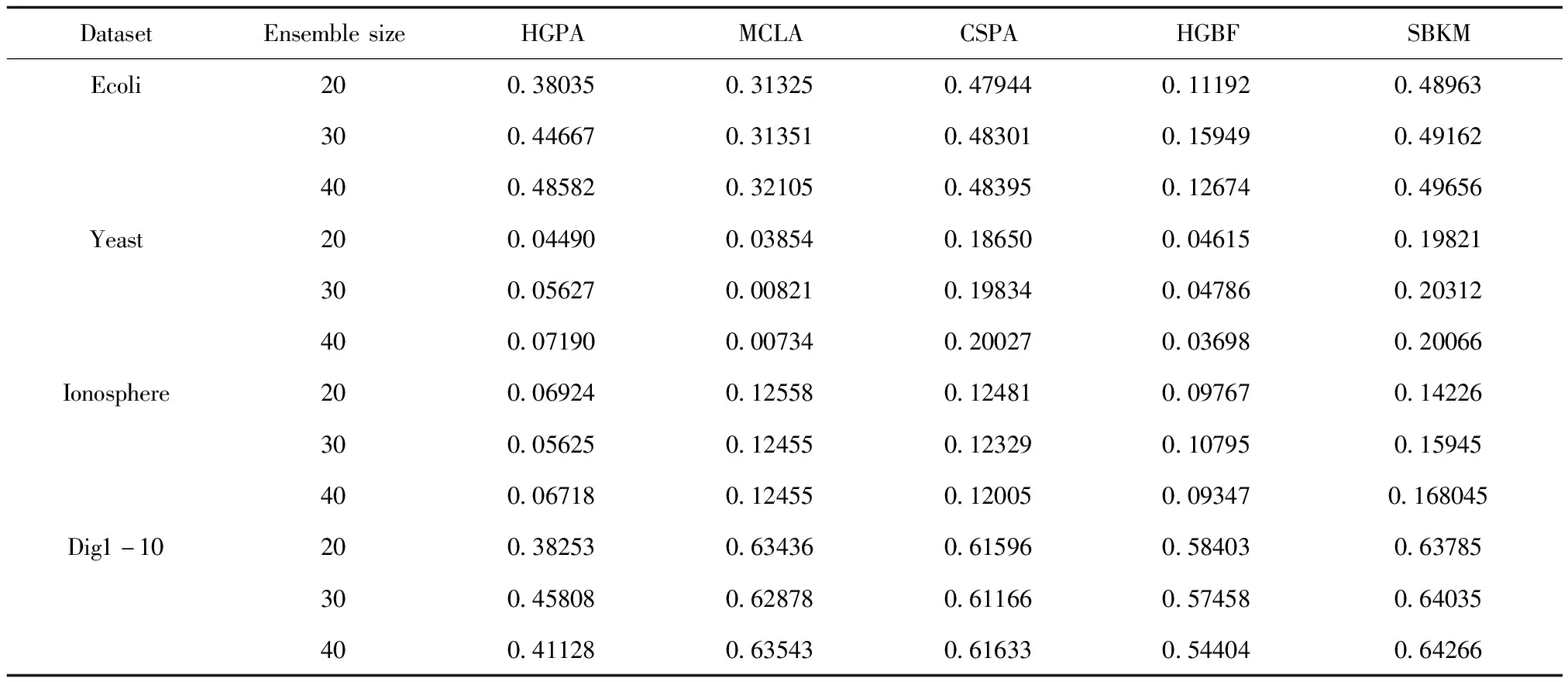
表3 标准互信息的平均值(最优值标黑)

在实验的第二部分，选取数据集(Zoo，Solar，Auto)作为数据输入与谱聚类算法(Ncut)相比较，在这部分实验中分别独立运行SBKM算法和谱聚类算法(Ncut)20次，且在SBKM算法中ensemble size分别设置为20，30，40，记录每次实验的标准互信息并求20次的平均值，实验结果如表4所示。

表4 标准互信息的平均值(最优值标黑)

实验结果如表3，表4所示。根据表3可知，本文提出的算法SBKM在一些方面优于其它聚类集成算法。在NMI评价指标下，SBKM算法在这4个数据集中取得了最优结果，相较于其它几个对比算法有效地提高了聚类集成的质量。根据表4可知，在其它3个数据集中也取得了较好的结果，这说明聚类集成的质量比单一聚类要好。SBKM算法能够有效使用基聚类与样本之间的潜在信息来提高聚类质量。

5.3 收敛性分析

本文提出的一种基于谱聚类的双边聚类集成算法(SBKM)。通过实验研究最终得到的S，P，Q三个参数都是最优值，使得目标函数值最小即目标函数收敛。假定ensemble size 为20时，SBKM算法在7个数据集上的目标函数值如图1所示。SBKM算法最终都能在数据集上目标函数达到最终的收敛。

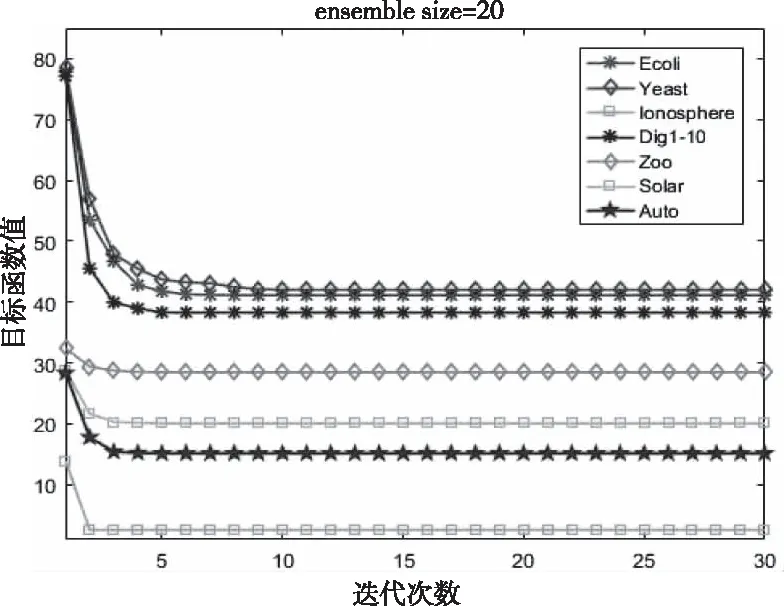
图1 迭代过程中的目标函数值

5.4 基聚类大小的讨论

为了研究基聚类大小对本算法聚类集成准确度的影响。在本实验中，从谱聚类生成的多个聚类结果中选择基聚类(ensemble size分别为：20、30、40、50、60)。在数据集Ecoli、Ionosphere、Yeast、Dig1-10上分别独立运行SBKM算法20次，记录每次算法的标准互信息并且计算20次算法的标准互信息的平均值，如图2所示。

在Ecoli、Ionosphere、Dig1-10数据集上随着基聚类的增大，标准互信息的平均值也逐渐增大而在Yeast数据集上基本不变。即随着基聚类增大能够对本算法聚类集成算法的准确度有一定程度的提高。

6 结论

本文提出了一种新的聚类集成算法。SBKM算法在生成阶段通过谱聚类(Ncut)算法获得基聚类，并通过对基聚类的选择，尽可能的挖掘数据的潜在信息，从而提高基聚类的质量。在集成阶段通过双边聚类充分利用将样本与基聚类之间的潜在信息，同时对样本和基聚类进行聚类，直接得到最终的聚类结果，并且能够在七个数据集上有较好的表现。相比于其它聚类集成算法文中的算法不仅能够充分的利用数据之间的潜在信息，而且能够之间得到最终的聚类结果而不需要借助其它传统聚类算法。