改进K-means加权自适应多视图数据聚类算法

李丽亚，闫宏印

(1.太原工业学院，山西 太原 030008；2.太原理工大学，山西 太原 030024)

1 引言

随着信息技术的高速发展，数据信息量和数据信息种类越来越多，将这些数据看成多个特征集合，并把每一个具有特征的集合比作一个视图，这样便构成了多视图数据。例如：若想识别一个人，可以结合他的声音、长相、外形等特征对其进行辨别。因此对多视图数据有以下定义：同一个物体从不同角度观察所产生的异构特征数据，叫多视图数据[1-4]。现阶段由于测量方法的多样性，多视图数据在各行各业中广泛存在。对数据进行描述时可以通过对不同的视图从不同的角度进行分析，如何对多个视图数据采取高效聚类是当前研究领域的一个重点问题。

文献[5]提出一种样本加权的多视图聚类算法，对每个样本的不同视图作加权处理，然后采用交替方向乘子算法实现自适应学习。实验结果表明，该算法不仅体现了样本的差异性，还能够很好地刻画出视图的重要性，但是该算法提出的模型在视图数据上的聚类效果相对较差。文献[6]提出一种鲁棒自加权的多视图子空间聚类模型，该模型利用范数处理多视图数据的平方差，并通过范数对数据的离群点进行分析优化，有效地解决了普通点和离群点对多视图数据性能的干扰，但该方法不能使模型尽可能的收敛到局部极小值，因此导致模型不能取得最优求解策略。文献[7]提出了一种大规模多视图数据的自降维K-means算法，通过找到某一个视图上的最优子空间达到多维数据的自动降维处理，并利用非负矩阵分解的方法对有损函数重新构建，达到视图数据共享、多视图数据信息互补的目的，完成多视图数据的聚类。实验结果表明，该算法能更准确的聚类，但就大规模多视图数据的计算复杂度而言，还需进一步优化。

基于现有研究成果及其优缺点，本文提出了一种基于改进K-means加权自适应多视图聚类算法，针对离群点对数据模型的影响，对数据条件进行优化，通过改进目标函数系数，平衡多视图数据的大小误差。在进行优化之前，通过损失函数，确定多视图不同簇的聚类中心，并结合拉格朗日乘子法，将多视图数据信息进行聚类。

2 基于加权自适应的多视图数据聚类算法

对于多视图聚类问题，大多数学者采用学习样本上不同类型信息对节点簇结构有差异的K-means型算法。这种算法将多视图的两种类型信息映射到同一个维度空间上，再通过对其进行融合，得到具有统一的簇中心，其目标函数用公式表示为

(1)

虽然以上方法可以对不同样本的两种类型信息进行重要性的差异学习，但是在信息融合过程中，需要将空间进行维度变换，可能导致一些信息的损失，而且同维度变换会增加算法的复杂性，使得对节点簇结构的差异性缺乏灵敏度，因此本部分内容提出加权自适应多视图聚类算法。

如果有Nw个视图，所有视图的数据用公式表示为

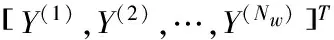
(2)

由以上的目标函数可以求得多视图的矩阵分解模型，公式表示为

(3)

大多数多视图子空间算法都可以取得很好的效果，但由于数据具有误差性，普通的多视图数据不能保证低秩的性质，所以不能直接在数据上做矩阵分解。于是引入约束条件Y(w)=E(w)WT，从而使目标函数达到最优状态，用公式可表示为

(4)

由上述公式可知，模型对数据误差较大的离群点很难做到多视图数据的有效融合，只能处理误差小的多视图数据。但现阶段大多数算法都忽略了离群点对数据模型的影响。针对这种情况，假定多视图数据矩阵Y用公式表示为

(5)

其中，e表示数据的稀疏误差矩阵；H表示数据的低秩数据矩阵。将这种模型应用到多视图数据中，则加权自适应多视图数据聚类模型用公式可表示为

(6)

由于数据中的小误差对多视图数据结果有影响，因此对数据条件H(w)=E(w)WT进行优化处理。把Frobenius范数作为条件进行改进，起到对多视图数据加权的作用。用公式表示为

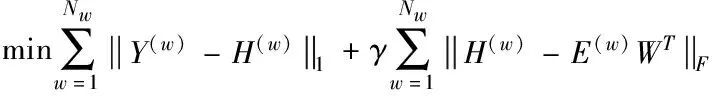
(7)

其中，γ表示目标函数系数，在平衡多视图数据的大小误差上起着关键性作用。除此之外，还需结合自由度问题。假设存在某个可逆矩阵Q，满足如下条件

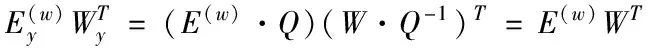
(8)

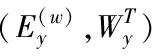
(9)

3 多视图数据的K-means优化理论

为了进一步求解到最小值，本节利用动态规划的方法将目标函数进行分步优化。对于多视图数据中的任何一个视图数据，进行QR分解处理，将U(w)作为正交矩阵Q的初始值。在含有噪声的空间中，把多视图数据看成整个簇，根据K-means优化理论，可知

(10)

u(w)表示视图常数。在进行优化之前，引入损失函数，公式表示为

(11)

其中，η(w)表示自动学习的权重系数；σ是权衡权重系数的分布式参数。由于每个视图数据都是不同的，因此通过η(w)给信息量较多的视图分配较大的权重；反之，给信息量较少的视图分配较小的权重，这样便可通过权重系数减少数据对多视图聚类的影响。算法的最终损失函数作如下变形处理

(12)

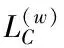
(W(w)TE(w)TY(w)-W(w)TE(w)TF(w)GT)T}

(13)

其中，N(w)表示对角矩阵，该对角矩阵的对角元素是其对应视图中行向量函数，公式表示为

(14)

综上可知，J是关于F(w)的凸函数，对其进行求导，可以得到

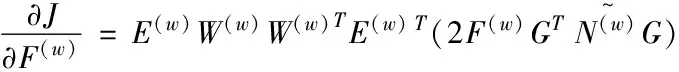
(15)

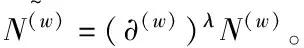
(16)

其中，G表示离散的矩阵向量，为了达到优化离散矩阵的目的，可以为每个多视图数据分配指示向量。保持F(w)和G不变，确定多视图不同簇的聚类中心，通过计算，可以得出

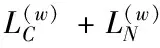
(17)

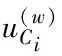
(18)

至此所有视图数据信息聚类优化已完成。

4 多视图数据集及衡量指标

4.1 数据集描述

为了评估本文所提出改进K-means加权自适应多视图数据聚类算法的效果，对不同多视图聚类模型进行对比分析，选取存在多视图差异的3个数据集，和不存在差异的2个数据集作为比较，分别为WebKB、Wiki、VOC和Handwritten numerals、Caltech101-7。下面分别介绍这5个数据集的特点。

1)差异性数据集描述

WebKB数据集：该数据集分别包含{195，187，230，265}个样本，每个样本对应的维数分别为{195，1703}维、{187，1703}维、{230，1703}维、{265，1626}维。该数据集涉及了5个类别，分别为：工程、学院、课程、员工、学生。

Wiki数据集：该数据集经常用在跨模态的检索环境中，其中包含训练样本2173个、测试样本693个，类别10个。每个视图都应用128维的特征向量视图和10维的主题描述向量视图。

VOC数据集：该数据集是一个自然图像数据集，每一张图片都包含512维的GIST文本特征和399维的TF文本特征，整个文本涉及了20个类别。

2)相同性数据集描述

Handwritten numerals数据集：该数据集包含10个类别的2000个手写数据。选取的特征分别为85维的FOU特征、73维的KAR特征、225维的FAC特征、231维的PIX特征和56维的ZER特征的共计5个视图数据。

Caltech101-7数据集：该数据集经常用在对象识别的环境中，包含1526张视图，7个类别，6个特征，视图对应的特征维数分别为49维、51维、365维、2095维、623维、1039维。

4.2 数据集度量标准

本文采用4个性能评价指标对多视图聚类算法进行衡量，分别为F-meansure、正确率、RI以及Speedup性能指标。

F-meansure：该指标的公式表示为

(19)

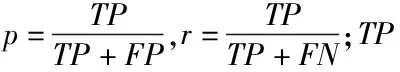
正确率：该指标的公式表示为

(20)

其中，n表示多视图数据中正确划分的样本数；N表示多视图数据样本总数。

RI：该指标用来评价2个聚类划分效果的相似程度，公式表示为

(21)

其中，Ia表示在不同簇被划分到不同簇的多视图样本数；Ib表示在不同粗被划分到童簇的多视图样本数；Ic表示在童簇被划分到不同簇的样本数；Id表示在通粗被划分到通粗的样本数。

上面三种评价指标，得出的数据结果越接近1，说明聚类效果越好。

Speed：该指标是用来评价多视图数据集运行时间的。公式表示为

(22)

其中，t表示增量算法对普通聚类算法聚类所运行的时间；T表示增量算法对数据集聚类所运行的时间。Speed越大表示增量聚类算法运行时间越短，反之时间越长。

5 实验结果及分析

对多视图数据进行分块处理时，本文采用五种分块模式，分别占比为：25%、50%、75%和100%，并且采用随机分块模式。为了避免数据对多视图聚类结果的影响，本文取50次视图数据的平均值作为实验结果。分别在WebKB、Wiki、VOC、Handwritten numerals和Caltech101-7数据集上进行实验，结果如表1～表5所示。

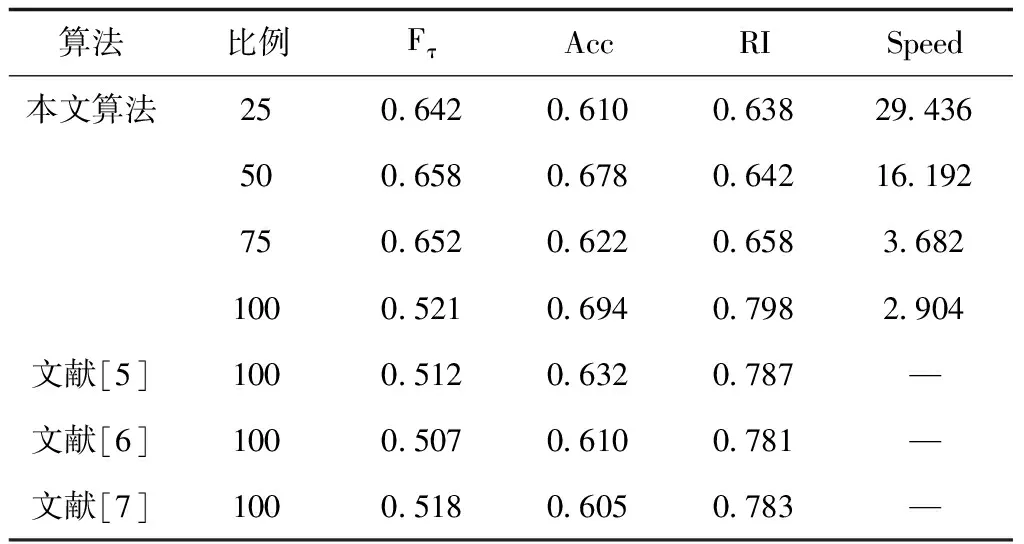
表1 WebKB数据集上的实验结果

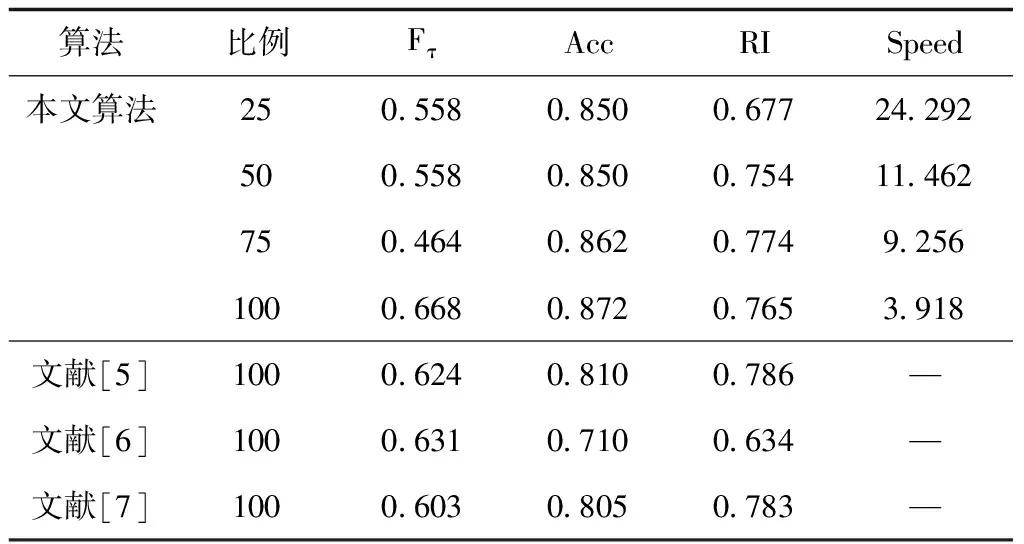
表2 Wiki数据集上的实验结果

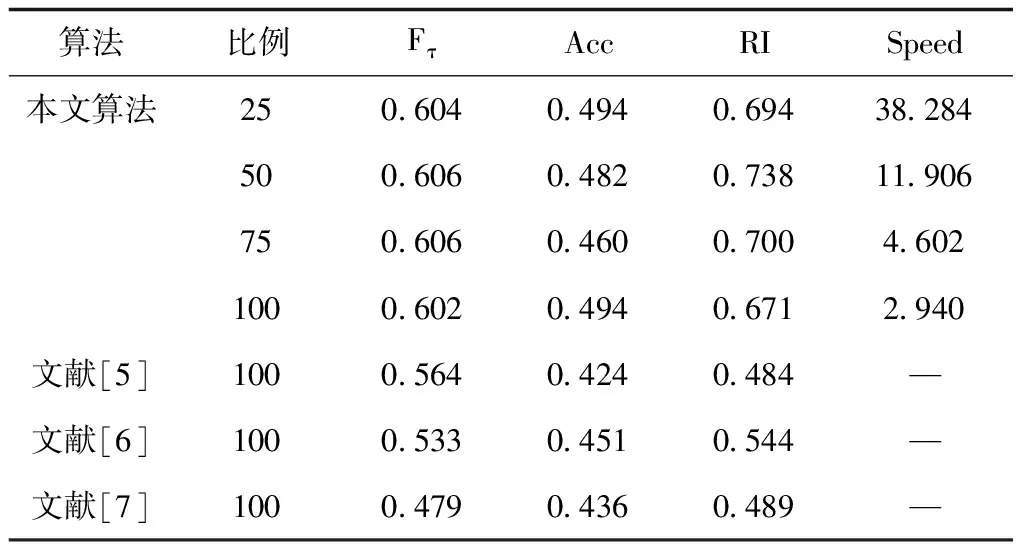
表3 VOC数据集上的实验结果

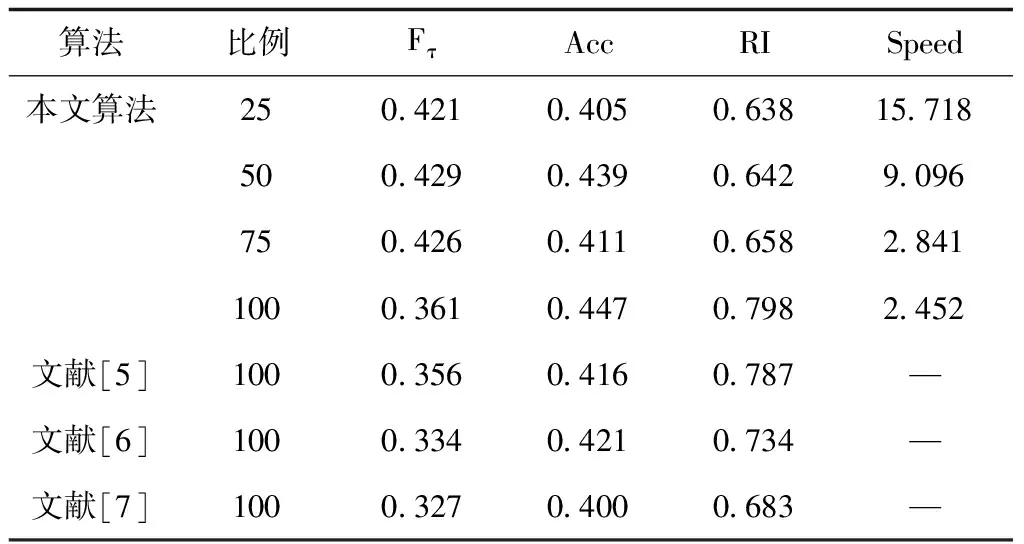
表4 Handwritten numerals数据集上的实验结果

表5 Caltech101-7数据集上的实验结果

通过对多视图数据聚类性能进行分析，从表1-5可以看出，本文算法在5个数据集上均有较高的正确率和RI值，以及较高的F-meansure值，说明本文所提出的算法可以保证多视图数据的聚类准确性与聚类精度。另外，从表中可以看出，在5个数据集上，当视图数据块为多视图整个数据集的25%时，算法的Speed值最大。随着数据块所占比例的增加，Speed值越来越小，其原因是随着数据块的增加，加权自适应聚类算法计算量越大，导致聚类时间越长。因此在多视图数据中所分的数据块越大，本文的算法越能减少聚类运算时间。

6 结束语

由于现阶段所研究的多视图聚类算法运行时间较长且性能欠佳，本文将K-means算法进行改进结合加权自适应算法，实现数据的可分性，即便在视图数据较多的情况下，也能大大提高算法的聚类效果。基于MATLAB平台，采用F-meansure、正确率、RI和Speedup作为性能指标，针对WebKB、Wiki、VOC、Handwritten numerals和Caltech101-7进行仿真验证。仿真结果表明，本文所提出的算法与文献[5]、文献[6]和文献[7]相比，不仅提高了多视图数据的聚类准确性与精度，而且还明显地减少了运行时间，降低资源消耗。说明在处理大规模多视图数据时，本文所提方法具有良好的可行性，拥有较高的实用价值。