一种特定栅藻细胞形成机理的仿真分析

王远弟，李炎芮

(上海大学数学系，上海 200444)

1 引言

绿藻作为地球上的一个古老的物种，它和陆生植物的联系得到了广泛的认同[13]。绿藻本身也有大量的物种，据统计大约6000多种，比如：鞘毛藻、栅藻、盘星藻等。本文讨论的只是其中一种绿藻--栅藻，准确来说是以一种龙骨栅藻为例，仿真分析其结构形态的成形机理。几种比较具有代表性的绿藻细胞成形或分裂机制已经有了研究。以鞘毛藻为例，其形状多为一种平板盘形结构，它的细胞是在平面方向不断生长，也就是向外扩张，在此过程中还伴随着不断分裂。研究表明，鞘毛藻在生长过程中，细胞分裂满足“最短分割线原则”，即所谓的Errera律[1]。这种分裂方式，或者是分裂边界的确定方式，与数学上的“隔墙”问题(fencing problem)有着密切联系[9]，10]。

其它绿藻细胞是否也符合上述“隔墙”问题模型？事实并非如此，不同的绿藻细胞分裂和繁殖方式都有自己的特点，比如盘星藻与栅藻，它们的分裂方式与鞘毛藻不同，似乎有“更优”的分裂方式。对于常见的盘星藻和栅藻细胞，尽管它们的生长分裂过程有类似之处，但是形状上这两种细胞群体有很大的差别。因此，不同绿藻细胞的成形机理是不同的。

盘星藻呈盘状结构，在平面上展开2n个细胞，细胞之间以一定的方式相连接。根据其连接方式和生物学属性，盘星藻细胞的成形模拟是构造了泡泡细胞模型[11，12]。所谓泡泡模型，用平面二维几何来解释是指：给定所有边长长度之和为一个固定值，指定其围成面积最大的固定数量的平面区域。注意到细胞间隔膜与细胞和外边界之间隔膜性质上的差别，也就是说细胞之间和细胞与外界之间存在不同的钙粘性蛋白作用。例如细胞之间存在E-钙粘性蛋白和N-钙粘性蛋白这两种蛋白的作用，而在外边界上则只有E-钙粘性蛋白，这种差异直接影响到细胞不同位置的边界粘性和张力的差异[3，11]。

栅藻在外观形状上与盘星藻或鞘毛藻有明显的差别，成形机制上它与盘星藻相似，都是从母体分裂出来的时候就已经定形，然后只是不断生长。不同于盘星藻的是，盘星藻细胞是不断生长和分裂，从而形成一个巨大的盘状细胞盘[10]。栅藻细胞则是成纵向一列(或两个并行列)排列。这里以龙骨栅藻为例，是细胞纵向单列(参见图2)。

本文主要研究栅藻细胞的形成机理，仅以2个细胞组成的群体为例进行分析。除了考虑到细胞之间的钙粘性蛋白，即E-钙粘性和N-钙粘性两种蛋白对两个细胞之间的粘性和张力作用外，新增加了一个影响因素，考虑了横向和纵向之间受到不同的粘性和张力作用，即假设横项和纵向之间存在一种受力差异。这种受力差异，根据本文后面的建模分析，导致了栅藻在形态上的变化。

2 栅藻成形模型

本文主要研究与龙骨栅藻形状类似的一类绿藻。如图2(a)为实际细胞红外影像图。根据实际受力和形态分析，引入不同参数构建椭圆模型。作为对照分析，这里也引入泡泡模型做分析。

2.1 椭圆模型推导

基于目前已有的泡泡模型假设，两个细胞的边界有一部分相连。相连的公共边界记为Lb，另外两条边界分别记为La和Lc，如图1。细胞的两条边界交点分别记为P(t*)，P(tc)和P(t*)，P(T)，同时也为了讨论方便，使用参数方程来表示边界，其中t为参数；规定三条边界的方向如下：

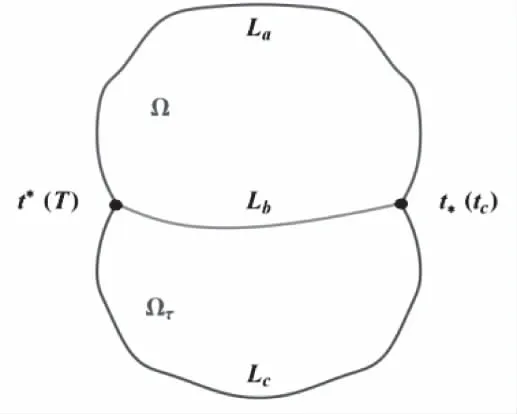
图1 模型假设示意

La(t*→t*):P(t*)延上边界即La本身到P(t*)；Lb(t*→tc):P(t*)延公共边界即Lb本身到P(tc)；Lb(tc→T):P(tc)延下边界即Lc本身到P(t).

考虑到细胞群外边界(简称“外边界”)和细胞群组之间细胞间隔(简称“内膜”)粘性和张力的差异，使用了一个参数来表示这种差别。提出细胞的形状要考虑横向和纵向的受力差异，同样引入了参数来表示这种差异。构建如(1)带有约束条件的Lagrange函数，以两个细胞的面积作为目标函数，整体加权周长l=|L|=|La∪Lb∪Lc|(外边界和内膜弧长之和)为约束条件。Lagrange函数为

(1)

这里的τ是上、下细胞Ω和Ωτ面积之间的比值，即|Ω|:|Ωτ|=1:τ，外边界和内边界粘性和张力系数之比1:λ；而系数α1和α2表示细胞在横和纵方向(即x-轴和y-轴方向)所受不同的拉张差别系数，其中也体现出了外边界和内边界的差别。具体地，设

三条边界曲线对应的参数t的范围如下

La:t∈[t*，t*]，Lb:t∈[t*，tc]，Lc:t∈[tc，T].

其中端点处满足

(φ(t*)，ψ(t*))=(f(tc)，g(tc))=(p(tc)，q(tc))，

(φ(t*)，ψ(t*))=(f(t*)，g(t*))=(p(T)，q(T)).

对于此函数的处理采取了摄动法，以下是简单的计算过程。此外，为了使函数表达

式简单，引入了Wronski行列式

那么，Lagrange函数可记为

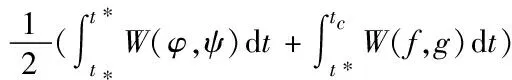
对于满足极小加权周长的曲线L，任意一点的摄动都会改变面积。对于三段曲线，分别引入三组对应的扰动曲线

在L1=La1∪Lb1∪Lc1的扰动下，该函数可变为

J(L+εL1)

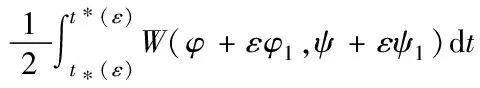
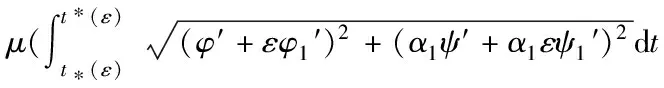
现在寻求驻点，为此计算关于ε的导数：

且在驻点处即ε=0时有

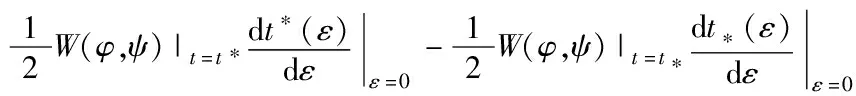
(2)

先处理方程(2)中所含的积分式子，积分项为

(3)

其中的t*=t*(0)=t*(ε)|ε=0.

注意到摄动曲线的任意性，以{φ1，ψ1}为例，找到其对应的积分并将其化简，则有：

利用摄动函数的任意性，得出上边界曲线La满足的方程为

(4)

不难得出方程(4)的解为

(5)

同样地，另外两条曲线所满足的方程的解分别为

(6)

(7)

下面考虑端点处的边界条件，如图1中右t=t*(tc)和左t=t*(T)两个端点处满足

(右端点)

{φ(t*)，ψ(t*)}={f(tc)，g(tc)}={p(tc)，q(tc)};

(8)

(左端点)

{φ(t*)，ψ(t*)}={f(t*)，g(t*)}={p(T)，q(T)}.

(9)

扰动后的边界条件如下

{φ(t*)+εφ1(t*)，ψ(t*)+εψ1(t*)}

={f(tc)+εf1(tc)，g(tc)+εg1(tc)}

={p(tc)+εp1(tc)，q(tc)+εq1(tc)};

{φ(t*)+εφ1(t*)，ψ(t*)+εψ1(t*)}

={f(t*)+εf1(t*)，g(t*)+εg1(t*)}

={p(T)+εp1(T)，q(T)+εq1(T)}.

对ε求导，且当ε=0时，有:

{φ′(t)t′+φ1(t)，ψ′(t)t′+ψ1(t)}|t=t*

={f′(t)t′+f1(t)，g′(t)t′+g1(t)}|t=tc

={p′(t)t′+p1(t)，q′(t)t′+q1(t)}|t=tc;

{φ′(t)t′+φ1(t)，ψ′(t)t′+ψ1(t)}|t=t*

={f′(t)t′+f1(t)，g′(t)t′+g1(t)}|t=t*

={p′(t)t′+p1(t)，q′(t)t′+q1(t)}|t=T.

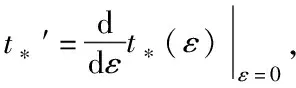
(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

分别讨论两个端点的情况。对于在t=t*(tc)处的相关项，将上面方程(10)-(19)中对应的表达式带入驻点条件(2)和(3)，结合边界条件(8)-(9)中的项，取出只含有t*，tc的部分(不含纯积分项)，再利用导数t*′和tc′的表达式，整理可得

=0.

这就得出驻点条件(2)中的非积分项，利用关于摄动项端点处f1(tc)，g1(tc)，p1(tc)，q1(tc)的任意性，这些项的系数只能全部为0，也就是对应项的系数如下

f1(tc):

g1(tc):

p1(tc):

q1(tc):

再通过简单代数运算，整理在t*，tc处满足边界条件:

(20)

(21)

(22)

类似得出，在t=t*以及t=T处满足的边界条件为

(23)

(24)

(25)

由方程(5)，(6)，(7)可以得出，该模型是一个椭圆模形，还可以利用边界条件来验证栅藻细胞与其的拟合程度。其中α1=α2=κ=a/b为椭圆长短轴之比，直线Lb记为(f(t)，g(t))=(t，0)，其它切线方向都是细胞外角切线方向。

2.2 椭圆模型分析

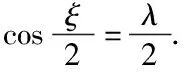
(26)

图2 两个栅藻细胞成形图及细胞仿真模型

为计算方便，假设长短轴之比为κ，即a:b=κ:1，结合点B(x1，y1)在椭圆上，满足椭圆方程的一般形式，可以得到ξ与x1的关系式以及y1的表达式如下

(27)

标准化细胞的面积，可以获取实际图像长短轴a和b的测量数据，根据上式之间的关系以及测量数据x1可以计算出夹角ξ，然后通过细胞面积为π可以获取具体的轴长。具体计算过程如下。

单个细胞的面积可以用积分表示为

简单化简一下，为

(28)

将(27)中的y1代入表达式(28)就通过实验测量数据κ和计算数据ξ，求出长轴a和短轴b，即

还可以计算出椭圆模型整体边界加权周长

“加权周长”L=外边界长度×1+内边界长度×λ.

具体计算公式为

2.3 二泡泡模型分析

理想模型的泡泡模型是不考虑不同接触面粘性与张力的差别[7]，而本文所考虑的泡泡模型两种类型的边权重是不一样的，在生物学上表现为两种不同的钙粘性蛋白E和N张力和粘性的差别。外边界和细胞间内边界的关系与方程(26)一致。具体的加权模型可以参加文献[11]，也就是细胞形状是两个圆周围成的圆盘(准确地说是圆盘的一部分)拼成的细胞组(如图3、4)。细胞之间的粘性和张力差别导致了外边界之间夹角的差别，参见方程(26)，其中ξ就是两条外边界之间切向的夹角。

上下泡泡面积相等，中间共边界，即图3中间直线段的长度决定于细胞之间的粘性大小。假设单个泡泡细胞的半径为R，每个细胞的大小即面积固定，统一假设为π，则

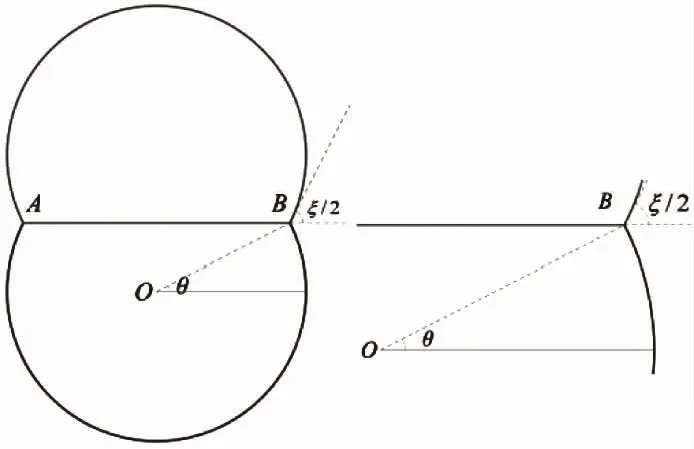
图3 双泡泡模型示意(右图为模型局部)

图4中，从左到右显示内膜张力由大到小(粘性由小到大)。

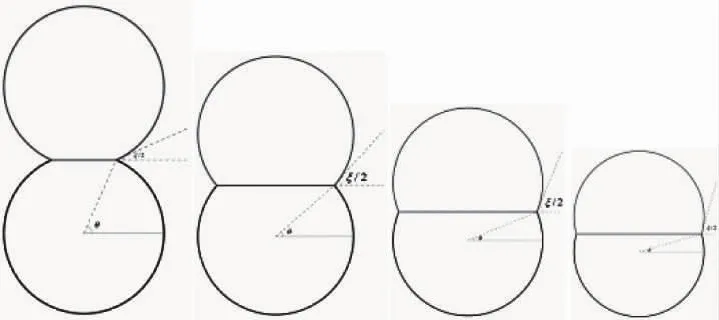
图4 不同权重对应的细胞模型

求解后得出泡泡模型的半径为

细胞间边界即内膜长度为

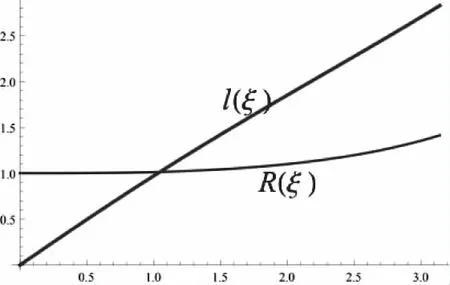
图5 半径R和细胞间的内膜长度l与细胞外角ξ之间的关系

所以，两条外边界和细胞之间的内边界构成的整体边界(加权)周长为

LB=2(2π-ξ)R(ξ)+2λR(ξ)sin(ξ/2).

注意到，关系式(26)表示的是细胞外边界与内边界之间的关系，计算双泡泡模型时外边界夹角ξ与椭圆模型是同一个，考虑前述椭圆模型算例中对应的λ值计算出相应的数值如下

ξ=1.47483，λ=1.48042，R(ξ)=1.04048，LB=12.0774.

3 数值模拟与验证

现针对上述两种模型进行数值模拟和验算，即椭圆模型和加权泡泡模型。

细胞之间内膜粘性和张力系数与外边界的之比为λ:1。如图2a)是一种龙骨栅藻外弯变种[14(lg)]，细胞之间的粘性大小直接影响了细胞外观形状。通过分析实验数据，得到如下信息

a:b:x1=108.25:75:172.142(像素比)，

这样，就会有：a/b=κ=1.44333.

由此，按照每个细胞面积为π的条件，椭圆模型可以算出相应参数，长轴a，短轴b，外边界夹角ξ，粘性和张力比λ以及总周长L近似数值为

a=1.29481，b=0.89710，ξ=1.47483，

λ=1.48042，L=12.4851.

照此算例，这里计算了33个来自各类文献和互联网的数据，图片来源参见参考文献[14]。所获得的算值如表1。分析结果见图6和图7，比较明显的是，长短轴之比κ正比于粘性λ和椭圆模型的全周长L，这与外边界的夹角ξ的情况正好相反。

图6 内膜粘性与张力系数λ与外角ξ和长短轴比κ之间的关系(左).细胞边界加权周长与ξ和κ的关系，右图表示椭圆模型

图7还显示了椭圆模型周长正比于长短轴之比κ和粘性λ，负比于外边界夹角ξ.图8也显示这33个实验数据对应的椭圆模型和泡泡模型之间(加权)总周长(length)的差别。普遍地，椭圆模型的总周长较泡泡模型长。还要注意到的是，泡泡模型的二次函数拟合吻合得比较好。

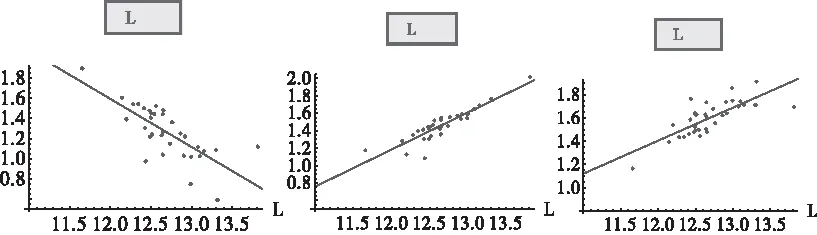
图7 椭圆模型整体边界加权周长L和外角ξ(左)，长短轴比κ(中)以及内膜粘性与张力系数λ(右)之间的关系图

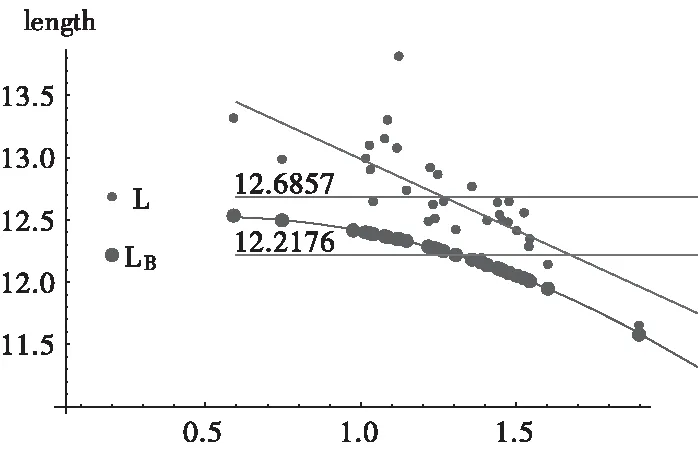
图8 两个模型整体边界加权周长和外角ξ之间的关系图

图8中，上部分为椭圆模型加权周长L，下部分为泡泡模型加权周长LB.

对于椭圆模型而言，实验数据显示，外边界夹角ξ直接影响整体加权周长，图8还显示出一种线性关系。(33个数据)这种相关性在图6和图7显示出一种一致性，实际上不难计算出三个相关系数，即椭圆模型加权周长L与外边界夹角ξ，长短轴比值κ以及内膜粘性与张力系数λ之间的相关系数(Corr)分别为

{Corr(L，ξ)，Corr(L，κ)，Corr(L，λ)}

={-0.515877，0.87514，0.508858}.

图9中，内膜粘性与张力系数λ与外角ξ和长短轴比κ之间的关系(左)。细胞边界加权周长与ξ和κ的关系，右图表示椭圆模型。

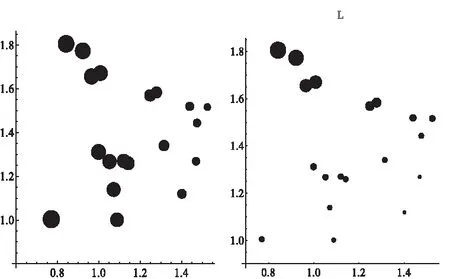
图9 19个数据实验(1)

图10中，椭圆模型整体边界加权周长L和外角ξ(左)，长短轴比κ(中)以及内膜粘性与张力系数λ(右)之间的关系图.

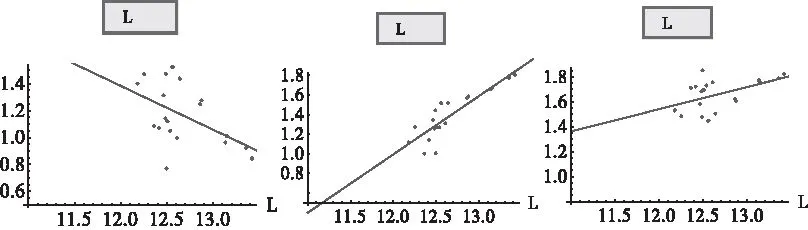
图10 19个数据实验(2)

图11中，两个模型整体边界加权周长和外角ξ之间的关系图。上部分为椭圆模型加权周长L，下部分为泡泡模型加权周长。

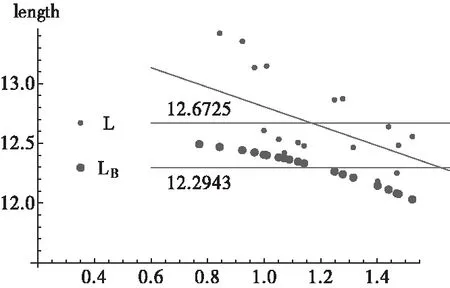
图11 19个数据实验(3)

在验证边界曲线关于端点处的切向夹角之间的关系时，注意整个三条边界的走向，如图2起始点在右端点B然后沿上边界抵达左端点(如图1中的t=t*处)，然后沿中间分隔线回到右端点B再由此沿下边界到了左端点(t=T)结束，各条曲线的切向量也是这样的方向。通过模型分析得出在两个端点处满足边界条件(20)-(25)。其中{f，g}，{φ，ψ}，{p，q}分别表示中间分隔线，上边界和下边界的方程，它们的导数表示切向。注意{φ′，ψ′}|t*表示到达该点，{f′，g′}|t*表示离开该点，其它类似分析。边界条件(20)-(25)表达的是切向量之间的关系式。图12显示的是左端点条件(20)即t=t*(T)点处三条边界切向量之间的关系实验验证，这里{f′，g′}={1，0}，κ1=κ(=α1=α2)表示两条外边界假设都是一样的，τ=1表示上下细胞面积相等。验证的方法是将表1的数据代入式(20)，实验数据计算后不是像等式(20)那样等于0，而是与0有误差，误差值(error)及其分布(frequency)情况见图12。实验数据计算后的平均误差为-0.158457，在这33个实验数据中误差小于均值的有15个。

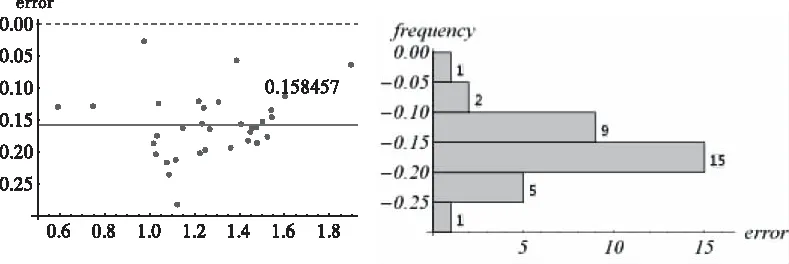
图12 对应于方程(20)的实验数据验证

另外一组19个实验数据带入(20)式验算之后的误差稍微小一些，均值为-0.131873，误差不超过均值的数据有9个(如图14)。

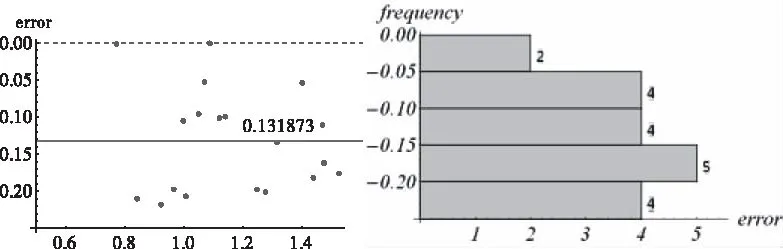
图14 另一组数据对应于方程(20)的实验数据验证

图12中，左图为33个实验数据误差分布情况，右图为误差分布直方图。

图13中，左图为33个实验数据误差分布情况，右图为误差分布直方图。

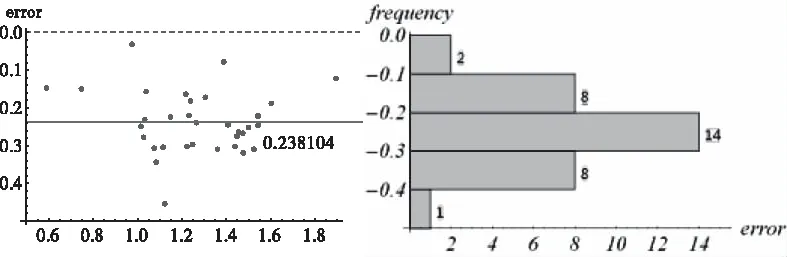
图13 对应于方程(21)的实验数据验证

图14中，左图为19个实验数据误差分布情况，右图为误差分布直方图。

图15中，左图为19个实验数据误差分布情况，右图为误差分布直方图。

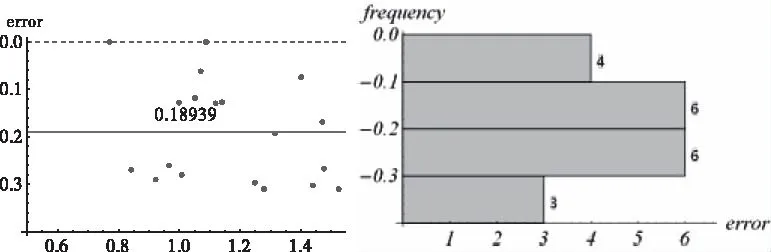
图15 另一组数据对应于方程(21)的实验数据验证

4 结论与分析

本文对一种特定栅藻——二细胞龙骨栅藻的成形特征进行了研究分析，得到了以下结论：

1)在现有绿藻细胞成形机理分析的基础上，提出细胞水平和纵向受力不均造成细胞形态变化。通过细胞受力分析和变分模型推导出这类细胞满足的椭圆细胞模型。

2)利用已有的细胞数据进行仿真分析，包括细胞各项数据的分布情况。同时，本文还针对性地对照已有的加权泡泡模型进行对照分析。结论是椭圆模型可以仿真模拟二细胞栅藻模型成形机制，尽管有一定误差。

本文的模型分析是简化考虑粘性和张力系数，也就是将边界(包括细胞内膜)上的粘性系数和张力系数合并成一个加以讨论分析，没有区别对待。后续可以结合借助于生物学实验详细区分这两种张力的各自作用差别，从而可以更精细的得出成形机理。此外本文仅仅是考虑了二个细胞构成的细胞群，对于更多的诸如4个、8个甚至更多的细胞群以及双列栅藻细胞也可以进一步分析，尽管可能会遇到更大的挑战。