逐级加荷条件下公路路基沉降变形监测仿真

沈世鑫，张有明

(青海民族大学土木与交通工程学院，青海 西宁 810007)

1 引言

由于我国软土占地面积分布较广，公路施工后的沉降变形问题一直是工程师们研究的热点[1]。因此，施工后的沉降量计算监测可以保证公路在运营时不会因沉降变形过大而导致公路的损毁，可以避免不必要的经济损失。当前的路基沉降监测方法是利用机床表层布设观测桩和沉降板进行监测，但是该方法成本过高又容易遭受到破坏，难以被广泛运用[2]。针对这一问题，贾亮[3]等人首先为了观察监测施工后的沉降变化情况，在路肩位置分布单点沉降计，然后分析了沉降随着时间和空间的变化规律，并以工后的沉降原位监测结果为基础，构建了沉降预测回归模型，完成路基沉降监测。但是该方法未利用有限元分析模型对土体的固结度进行计算，导致监测结果准确性较差。王翔[4]等人提出高速公路 运营期基础沉降长期监测。首先引入了太阳能供电的物联网技术，采用气压差高精度位移监测系统，实现了部分高速铁路的沉降监测。虽然该方法有效地解决了路基沉降变形的问题，但该方法未使用有限元分析模型对公路土体的沉降应力计算并进行沉降量变换，导致监测时间过长、实时性较低，影响了公路建设的施工进度。

针对上述问题，提出逐级加荷条件下的公路路基沉降变形监测方法。因为在计算土体应力应变关系时容易产生塑性屈服，所以首先利用受压屈服应力、受拉屈服应力计算材料的内摩擦力，分析当中的屈服关系，得到了弹塑性本构模型，并将该模型引入防止塑性屈服的产生，然后通过自动网格划分法建立有限元分析模型，再使用该模型获取计算固结度与沉降应力有限元参数，最后变换沉降应力得到沉降量，完成路基沉降变形监测。

2 Drucker-parger弹塑性本构模型

所提方法采用Drucker-parger为理想弹塑性本构模型[5]，如图1所示，其屈服准则为Drucker-parger屈服准则[6]。

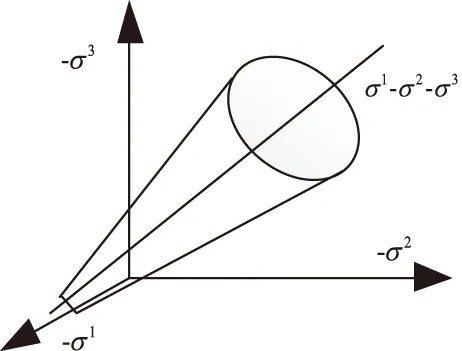
图1 Drucker-parger屈服面

2.1 屈服准则

采用该屈服准则的土体被称为DP材料。在DP材料中，受压的屈服强度远远大于受拉的屈服强度。首先利用受压的屈服应力、受拉的屈服应力计算内摩擦角和粘聚力，具体如式(1)、式(2)所示

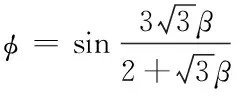
(1)

(2)

式中，β和σ与受压的屈服和受拉的屈服关系如式(3)、式(4)所示

(3)

(4)

设I为不变量，DP材料的屈服准则如式(5)所示

f=J21/2+aI-k=0

(5)

J2为应力偏张量第二不变量；a为材料的常数系数；k为材料屈服参数。因为屈服准则不包含强化准则，所以在此准则基础上建立的DP模型就是理想弹塑性本构模型。弹塑性模型的计算公式如式(6)所示

D1=σ1+σ2+σ3

(6)

因为该模型不包含强化准则，所以土体不会随着屈服而改变、屈服强度随着压力的增加而增加。因此，该模型可以有效提高路基沉降变形监测的实时性。

2.2 基于弹塑性模型的土体应力应变计算

首先，根据各层土体的应力状态不同，在某级荷载增量vγ作用下，有些路基可能处于弹性区。如果利用传统的弹塑性矩阵对土体进行应力计算[7]，有可能产生塑性屈服，所以使用弹塑性模型进行应力关系计算时，可以有效避免该现象。

假设土体应力状态的变化可能有以下三种情况：

1)如图2所示，F为曲面，如A点所示，如果加荷后应力落入弹性区，原始应力可能在屈服面上；如C点所示，加荷后落入屈服面以内，则该单元用弹性矩阵D计算；如B点所示，原始应力也可能在屈服面内，加荷后仍在屈服面以内，如G点所示，也用弹性矩阵计算。

图2 荷载增量应力路径

2)如图2中的AD线显示，原始应力在屈服面上经过加荷后达到了新的曲面F1，很明显发生塑性变形，因此需要用弹塑性模型D1计算。

3)BE线一部分BF处在弹性区，要用弹性矩阵D计算，另一部分FE在塑性区，要用弹塑性模型D1计算。

如图中的BE线显示，原始应力在屈服面以内，加荷后超过了原来的屈服面f，而达到了新的屈服界面f1，这时就会出现如何确定F点位置的问题，也就是说如何划分BF和FE的问题。

假设BF是直线，F为BE与屈服面F的交点，σB为B点的应力，E点的应力如式(7)所示

σE=σB=vσ

(7)

直线BF段各个应力分量的增量vσ1与BE段应力分量的增量比例如式(8)所示

vσ1=a1vσ

(8)

其中，a可由式(9)确定

(9)

设H0为硬化参数，根据加荷判断

f(σF)=F(H0)

(10)

因此，σF的计算如式(11)所示

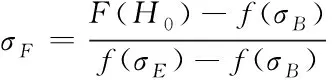
(11)

如图3所示，求得a值，则F点应力如式(12)所示

图3 弹塑性模型应力应变曲线

{σ}F=(σB)-a(σF)

(12)

3 基于有限元分析模型的固结度与沉降应力计算

为了使监测结果更加精准，所提方法采用自动网格划分法对公路路基进行有限单元网格划分[8]。因为考虑到土体的非线性性质[9]，塑性变形区域都利用了足够的网格密度，再使用自动网格划分法在路提土和地基土的接触面上采用共节点单元处理，完成有限元分析模型。最后，通过该模型得到某示例公路的有限元参数，计算土体固结度与沉降应力，作为后续的沉降量计算基础。

3.1 构建逐级加荷有限元分析模型

1)计算区域选定

所提方法选择非对称的路基断面，该断面左侧基土较为深厚，右侧基土为粉质沙土，附近为一山坡。其中，路堤底面长度为45米；设地基深度的方向是填筑高度的4倍，约20m；设地基的长度方向为路提底面的4倍，180m。

2)边界条件的确定

设上部为自由边界、左右两侧的水平约束、下部固定、为边界条件。根据路基的填筑具体情况将其划分为图中所示的3个区域。其中，路基填筑体为A区、地基土为B区、基岩为C区。

3)单元划分类型的选择

因为主要对2D有限元进行分析，所以6节点和15节点均可满足很多问题的计算精度要求。其6节点的单元插值为二阶，并通过3个高斯点进行数值积分计算得到单元刚度矩阵。而15节点三角形单元是一种非常精准的单元，在面对各类问题时都能保证精度很高的应力计算结果。积分过程为12个高斯点，其单元的插值为四阶。

其中，结构与界面单元的类型将自动和土体的单元类型相匹配。如果使用15节点的三角形单元进行自动匹配会需要较大的内存，而且运行和计算速度较慢。因此所提方法采用6节点进行自动匹配。图4是基于上述建立的有限元分析模型。

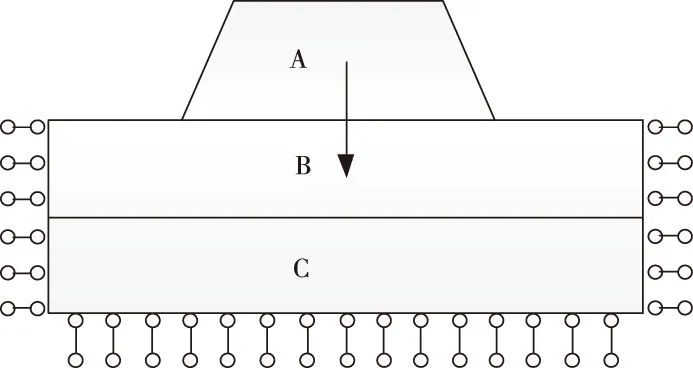
图4 有限元分析模型

3.2 固结度与沉降量计算

对土体的固结度和沉降应力进行计算能够有效地推进公路建设的施工进度[10，11]，实现公路路基沉降变形的监测，对可行的、经济合理的公路建筑工程有着重要的意义。

1)计算参数

如表1所示，通过有限元分析模型得到的某市级高速公路工程地质勘察资料，并通过该模型计算所用参数指标，提高监测结果的准确性。

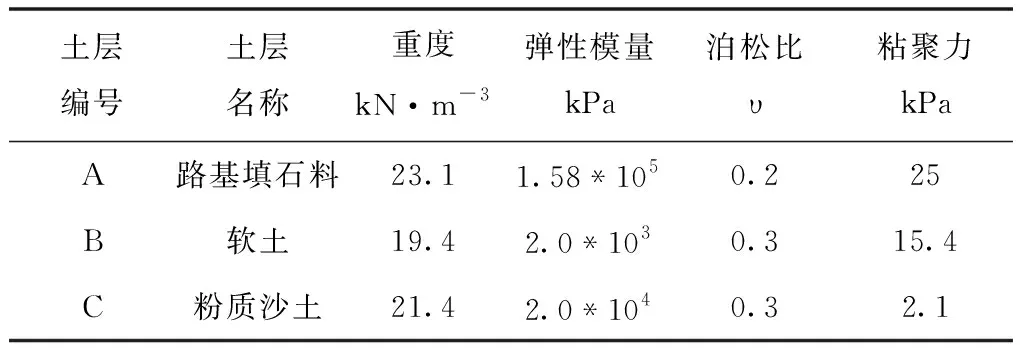
表1 有限元参数表

2)土体固结度计算

设土体为弹性体，体积压缩系数为Mv，表示常数量，路基z深处A点以下的厚度为(h-z)，土体全部的自重应力为引起压缩的应力，并以梯形分布在压缩层，A点的固结度计算如式(13)所示

(13)

3)土体沉降应力计算

其中，γ为土体的容重，如图5所示，设A点的沉降为0，如果填筑超过A点的高度，A点才会有沉降。当土填至与路面水平相同时，A点沉降的应力在(h-z)内分布，如式(14)所示

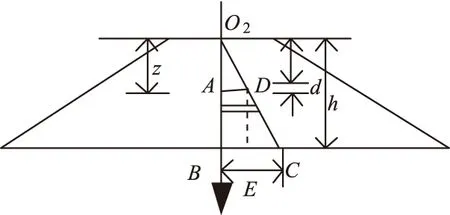
图5 公路路基沉降应力示意图

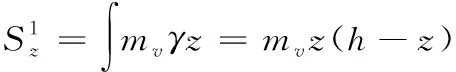
(14)

4 实现路基沉降变形监测

沉降量是确定路基沉降变形监测是否精准的重要手段。因此，在公路路面铺筑之前必须对路基的沉降量进行计算，保证运营时不会因路基沉降变形过大而导致公路的损毁。

以上述高速公路为例，通过表1观测数据，得到该条公路的路基沉降变形时间曲线，如图6所示。

图6 公路路基沉降变形时间曲线

首先，根据有限元分析模型得到的式(14)设任意时间t的预测沉降应力St的计算如式(15)所示

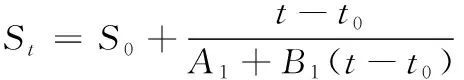
(15)

式中，当时间t趋向于无穷大时，对应的沉降应力就是最终沉降量S∞，对式(16)进行变换可得

(16)

其中，A1和B1关系由上述式(13)、(14)计算获得。再通过式(15)计算求出任意时刻t时的沉降量St，路基最终沉降量计算如式(17)所示

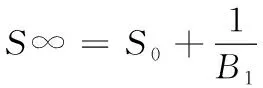
(17)

5 实验与分析

为了验证所提方法的有效性，分别对文献[3]方法、文献[4]方法和所提方法的实时性、稳定性、准确性进行对比测试。本次实验以正在施工的某市级公路作为实验对象，其公路路基沉降变形示意图如图6所示。

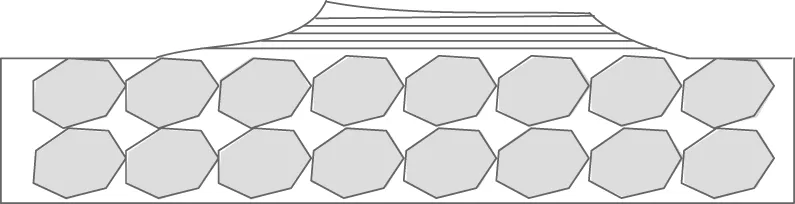
图6 某市级公路路基沉降变形示意图

5.1 实时性

图7是三种监测方法的实时性对比结果。从图中可以看出，三种方法的监测时间都随着公路的施工里程增加而增长，但是所提方法利用了有限元分析模型对土体的固结度进行了计算，及时反映了材料自身结构的应力变化，因此，所提方法相比其它两种方法拥有更优秀的监测实时性。

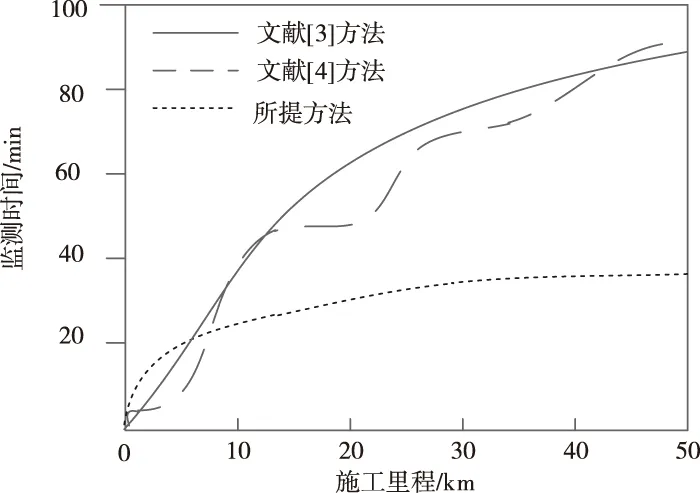
图7 路基沉降变形监测实时性对比结果

5.2 稳定性

由图8可知，文献[3]方法的稳定性系数虽然高于文献[4]方法，但是该方法在计算土体应力应变关系时未使用Drucker-parger弹塑性本构模型，也未利用有限元分析模型对路基的沉降应力进行计算，所以稳定性随着监测时间的增加而下降，而所提方法利用了弹塑性模型对土体的应力应变关系进行计算，分析了逐级加荷下增量应力的途径，并应用有限元分析模型计算了土体的沉降应力，确保了路基沉降变形监测过程中的稳定性。

图8 路基沉降变形监测稳定性对比结果

5.3 准确性

在实际的监测过程中，监测效果的好坏与公路建设施工的效率有着重要的必然关系。

从图9的对比结果可以看出，文献[4]方法的监测精准度高于文献[3]方法，但该方法监测过程未使用有限元分析模型计算公路的各项参数指标，使监测过程过于繁琐，出现监测精准度低，稳定性差的现象；然而，所提方法因为利用有限元分析模型准确地计算了公路的各项参数指标，所以精准度一直可以保持在95%以上，明显高于其它两种方法，因此，所提方法拥有更加出色的准确性。

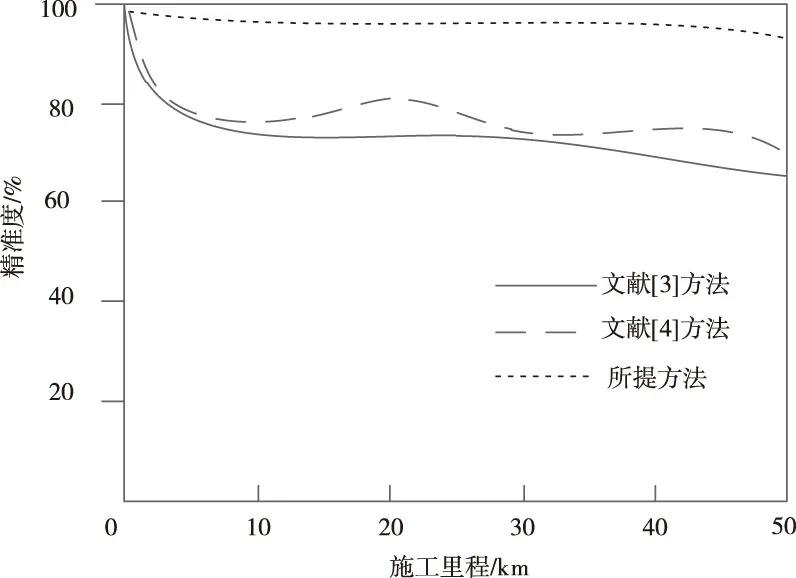
图9 路基沉降变形监测准确性对比结果

6 结论

在公路建设过程中，对路基进行沉降变形监测是十分必要的。针对当前方法的不足，提出基于逐级加荷的公路路基沉降变形监测方法。首先利用屈服准则构建弹塑性模型，计算土体的应力应变关系，再通过自动网格划分法建立有限元分析模型，并使用该模型获取有限元参数、计算固结度与沉降应力，最后将沉降应力进行变换得到最终的沉降量，利用沉降量计算方法实现公路路基沉降变形监测实验对比表明，所提方法拥有良好的实时性、稳定性、准确性，但该方法还尚有局限性，在接下来的研究里，会根据不同的路面特点实现应用性更强的监测方法。