基于分类规则挖掘的数据多标记特征分层识别
朱方娥,郭建方,曹丽娜
(石家庄铁道大学四方学院,河北 石家庄 051132)
1 引言
随着互联网信息技术的不断发展,每时每刻都在产生大量的数据,数据量级和数据复杂程度都达到了前所未有的规模。各种大数据混合在一起,将其中有价值和有意义的信息掩盖起来,导致数据利用率很低[1]。因此,如何提高大数据的利用率成为当下研究的重点。针对大数据存在的问题,首先要解决的就是将混合的大数据划分类别,从而为数据信息挖掘和识别或分类储存奠定基础。
关于上述问题的研究,在很多文献中都进行了相关研究。如,孙林等人[2]提出了一种基于邻域粗糙集的多标记专属特征选择方法,采用约简算法去除冗余特征的多标记特征,得到专属特征,保证了多标记分类,根据专属特征,采用邻域粗糙集构建多标记专属特征选择模型,完成了多标记专属特征选择,保证了邻域精确度。但是该方法进行多标记专属特征分层识别时,误识别的值较高,汉明损失较大,识别效果较差。王晨曦等人[3]提出基于信息粒化的多标记特征选择算法,利用改进的邻域信息熵对多标记特征进行选择,在6组数据集以及5个评价指标上的实验表明文中算法在分类上的有效性。但是该方法进行多标记专属特征分层识别时,拥有的特征子集较多,导致多标记特征识别结果不准确,降低了识别质量。
针对上述方法存在的问题,本文提出一种基于分类规则挖掘的数据多标记特征分层识别方法。该研究主要分为三个部分,首先对大数据进行降维处理,然后选取数据特征,组成数据样本多特征子集,最后挖掘数据分类规则,构建分类模型,实现数据多标记特征分层识别。最后与传统方法进行对比,通过仿真测试,证明了所研究方法的识别准确度,为多标签数据挖掘和利用奠定了基础。
2 基于分类规则挖掘的数据多标记特征分层识别方法
2.1 数据降维处理
大数据类型多样,因此一般都会存在维数灾难问题,导致数据处理和分析复杂度提高,因此在进行后续处理之前,需要进行数据降维,以便更好地认识和理解数据[4]。目前,数据降维方法主要分为两类:线性映射和非线性映射方法。其中主成分分析算法和线性判别分析方法为线性映射方法,非线性映射方法主要包括核方法(核+线性),二维化和张量化(二维+线性),流形学习方法。在这里采用非线性映射方法中的一种LLE(Locally Linear Embedding-局部线性嵌入)方法进行降维。该算法大致分为三个步骤:
步骤1:寻找每个样本点的k个近邻点;
步骤2:计算每个样本点的近邻点,获取该样本点的局部重建权值矩阵;
步骤3:根据步骤2计算结果得到该样本点的低维嵌入输出值。
虽然LLE方法能够解决数据维数灾难问题,但是降维效果易受到近邻点数量的影响,为此本章节通过构造近似重构系数,对重构误差加以约束,实现LLE方法的改进[5]。改进的LLE方法降维流程如下:
对于给定的高维数据集X={x1,x2,…,xN},xi∈RD,其中RD是D维数据,采样自d维流形,求低维坐标Y={y1,y2,…,yN}[6]。
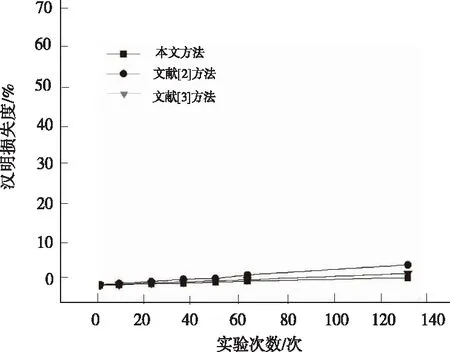
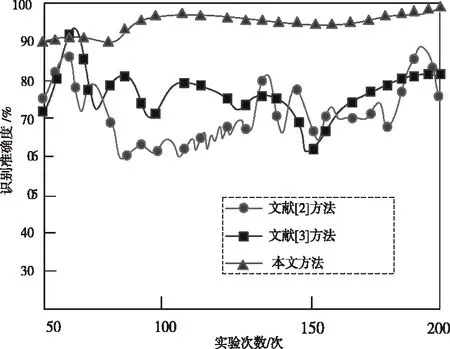
步骤1:寻找样本点xi的k(k (1) 步骤2:通过下述式(2),计算局部重建权矩阵(wij)。 (2) 其中,wij是xi与xij之间的权值。xij(j=1,2,…,k)为xi的k个近邻点。 结合限制条件,式(2)可改写为 (3) 其中 Zi=(xi-xij)T(xi-xij) (4) (5) 式中,Zi为第i个样本点的局部协方差矩阵;wi为第i个样本点的局部重建权值。 引入Lagrange乘子求解式(3),则有 ⟹Ziwi (6) 通常采取简单的求解方法,令Ziwi=1,来求得wi。 (7) (8) (9) 利用Lagrange乘子法,求得 (10) M=(I-W)T(I-W) (11) 一个多标签的数据拥有多个特征,但是不是每个特征都是有价值的,因此需要进行特征选择。特征选择是指从原始的特征空间中,根据一定的标准,进行特征选择,并构成特征子集[9]。 1)子集生成 特征子集的质量直接关系到后续分类识别的准确性。对于特征子集生成来说,关键点搜索策略的选择[10]。目前,特征搜索策略主要分为三大类,如下表1所示。 表1 特征搜索策略 2)子集评估 基于搜索出来的特征子集,需要依据一定的特征评价准则进行优劣评估,以判断其是否需要进行子集更新,从而保证选出来的特征是最优特征,提高最后分类识别的准确率。子集评估标准可以选择距离度量(欧氏距离)、信息熵度量,相关性度量,一致性度量。下面以信息熵度量为例进行具体分析。 (12) 其中,f是双伽马函数,k是近邻的个数,N是X中样本个数,nl是类l中样本个数,L是类别总数,s(n,k)是第N个样本到它的第k个邻居的二倍距离。 3)停止条件 停止条件是指给出的特征选择结束的条件。这个条件可以是以下四点: 条件1:特征搜索是否已经结束; 条件2:搜索的子集数量是否已经达到设定的数量; 条件3:特征子集是否为最优子集; 条件4:是否满足最大迭代次数。 特征选择基本流程如图1所示。 图1 特征选择基本流程 从海量数据中提取出所需要的有用信息或知识,是当前大数据挖掘领域研究的重点课题之一。纵观前人研究,发现大多数研究都是针对单标签数据而提出解决方法,因此当前的方法并不适用于多标签数据分类识别。基于此,根据上述特征选择,本文利用分类规则挖掘方法构建一个分类识别模型,实现数据多标记特征分层识别。分类识别模型如下图2所示。 图2 基于分类规则的分类识别模型 在整个基于分类规则的分类识别过程中,主要分为两个阶段任务: 第一阶段:挖掘分类规则。 分类规则是指判断数据所属类别的条件或准则。在这里以免疫算法为核心,进行分类规则挖掘。免疫算法是以生物免疫系统运行原理而研发的一种算法。免疫算法主要分为抗原识别,初始抗体的产生,亲和力的计算,记忆单元的活化,免疫克隆、变异和抑制、选择,种群刷新。基于免疫算法挖掘分类规则,具体过程如下: 步骤1:对个体(规则)进行固定长度编码,并随机产生初始化父代种群。 步骤2:计算个体的适应度。 步骤3:检验适应度值是否满足设定的标准。若满足,则需要直接跳到步骤6;若不满足,则继续进行下一步。 步骤4:对得到的k代种群进行克隆、变异和抑制、选择等一系列操作,得到新一代父代种群,然后跳转到步骤2,重新计算适应度。 步骤5:判断是否满足迭代终止条件。若满足,继续进行下一步,若不满足,则需要回到步骤2。 步骤6:对新生成的个体(规则)进行剪枝,得到挖掘出来的分类规则。 第二阶段:分类识别实现。 步骤1:输入训练样本,对分类识别模型进行训练。 步骤2:将测试样本输入到训练好的分类识别模型当中。 步骤3:利用分类规则,进行特征匹配,实现特征识别,完成数据分类。 综上所述,基于分类规则挖掘的数据多标记特征分层识别方法的具体研究流程如图3所示。 图3 数据多标记特征分层识别方法研究流程 基于分类规则挖掘的数据多标记特征分层识别主要分为三大部分,第一部分,进行数据降维处理,提升数据质量;第二部分,数据特征选择,为分类识别提供依据;第三部分,分类识别,实现数据挖掘。 为测试本文提出的基于分类规则挖掘的数据多标记特征分层识别方法在实际应用中的有效性,将文献[2]提出的基于邻域粗糙集的多标记专属特征选择方法与文献[3]提出的基于信息粒化的多标记特征选择方法作为对比方法,在MATLAB平台上进行仿真测试。 表2 仿真环境 本次仿真在美国加州大学机器学习数据集中选取个6组数据集作为样本,其样本情况如表3所示。 表3 样本数据情况 在MATLAB平台上运行仿真测试程序,仿真测试程序如下图4所示。 图4 仿真测试程序 设D为一个多标签评价数据集,包含|D|个多标签样本<〈xi,Yi〉,1≤i≤|D|,Yi⊆L,L是类别,H是分类器,Zi=H(xi)是H分类样本xi的标签集合。 1)汉明损失度(Hamming loss degree) 汉明损失度(Hamming loss degree)主要评价识别方法误识别的情况,其值越小,方法识别效果越好。 (13) 其中,Δ表示是真实标记集合与预测标记集合之间的对称差。 2)准确度(Accuracy) 准确度(Accuracy)主要评价准确识别数据类别的情况,其值越大,方法识别效果越好。 (14) 对本文方法、文献[2]提出的基于邻域粗糙集的多标记专属特征选择方法和文献[3]提出的基于信息粒化的多标记特征选择方法的汉明损失度进行对比分析,对比结果如图5所示。 图5 汉明损失度对比结果 根据图5可知,本文方法的汉明损失度仅为1%,而文献[2]方法和文献[3]方法的汉明损失度为6%和3%,说明本文方法的汉明损失度较低,方法识别效果较好。 为了进一步验证本文方法的有效性,对本文方法、文献[2]方法和文献[3]方法的数据多标记特征分层识别准确度进行对比分析,对比结果如图6所示。 图6 识别准确度对比结果 从图6中可以看出,本次所研究的基于分类规则挖掘的数据多标记特征分层识别方法的数据多标记特征分层识别准确度较高,说明本方法的识别效果较好,达到了本次研究的预期目标。 综上所述,大数据在诸多领域中都起到了重要作用,但是大数据往往具有海量性、混合性,导致数据挖掘率低,数据利用率下降。为此,本文进行了基于分类规则挖掘的数据多标记特征分层识别方法研究。该研究通过挖掘分类规则,通过分类,实现目标类型识别。最后经仿真测试,通过汉明损失和准确度值证明了本方法的分类识别效果更佳。然而,本文在实现研究目标的同时,还需要在更为丰富的语料库中进一步测试和探讨识别方法的各种改进思路,以期提高识别质量。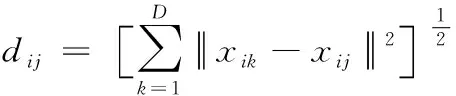
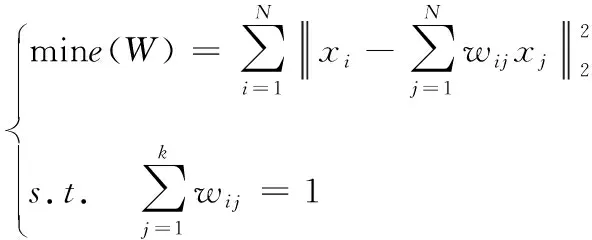
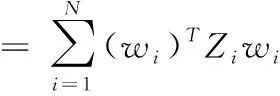
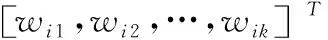




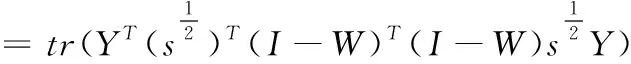
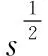
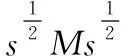
2.2 数据多标记特征选择

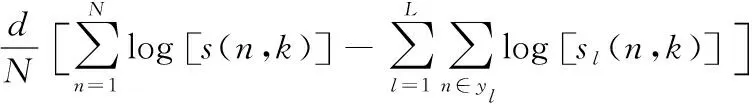
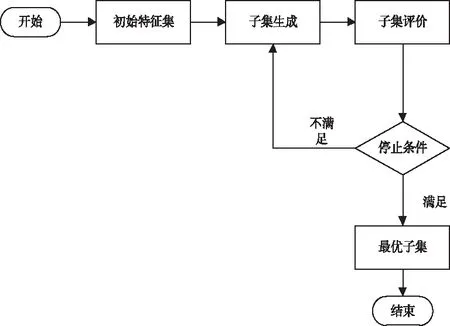
2.3 基于分类规则的分类识别
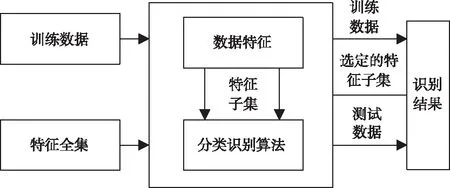
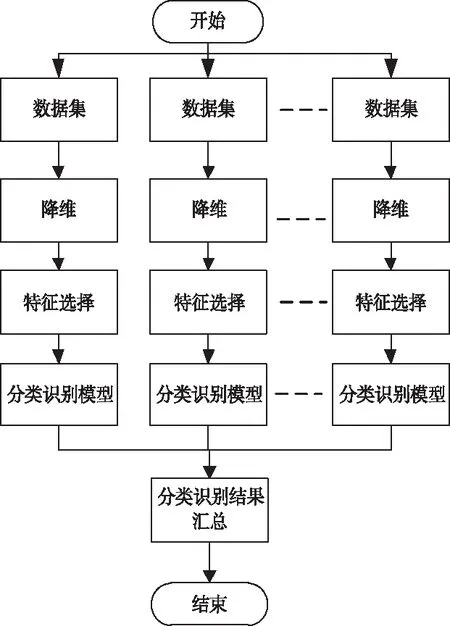
3 仿真分析
3.1 仿真环境

3.2 样本数据
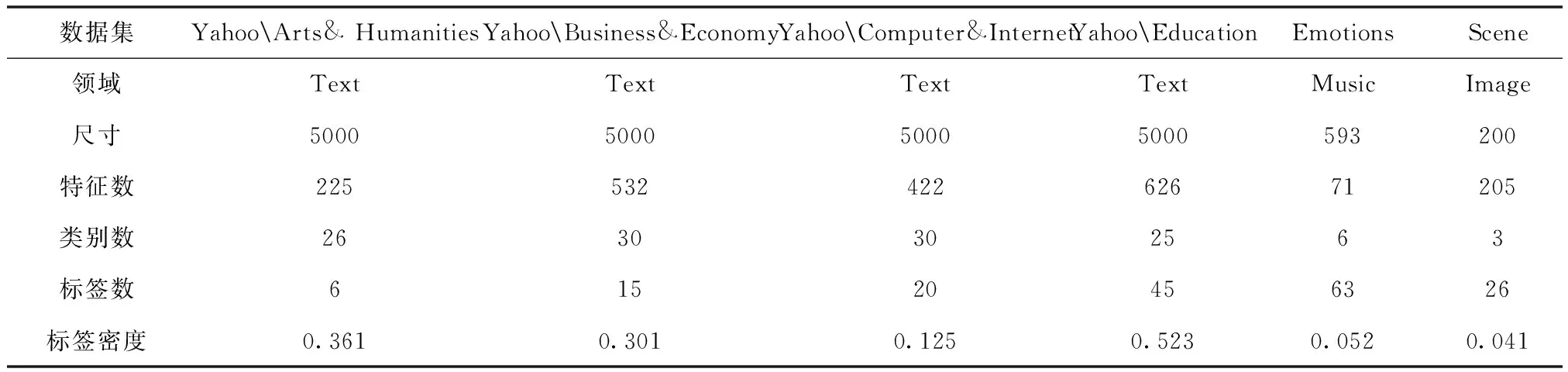
3.3 仿真测试程序
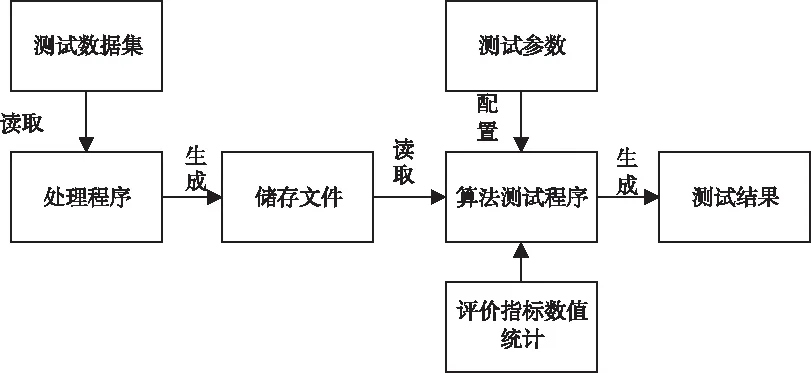
3.4 测试指标
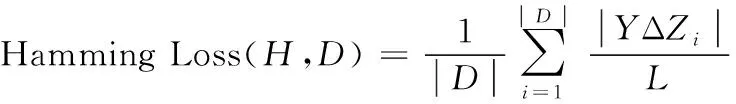
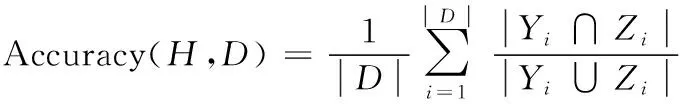
3.5 对比结果分析
4 结束语

