变结构三阶一致性无人机编队控制

王明华，胡士强

(上海交通大学航空航天学院，上海 200240)

1 引言

小型旋翼无人机体积小、重量轻、控制灵活、可悬停、成本低，已被应用于空中监测、火灾救援、摄影摄像等多个领域。而单架无人机受限于其载荷低和视野单一等弱点，不能满足高精度、多角度成像等行业应用需求。在航拍、空中监测等任务中，多无人机编队飞行可以扩大侦察、监测和搜索范围。在多机协同作业的情况下，良好的控制和编队设计可以大大降低单机失事对整个任务的影响，极大地提高了可靠性。无人机编队主要控制方法有长机——僚机型控制[1]、虚拟结构型控制[2][3]、基于行为型控制[4]、最优化控制[5][6]、人工势场控制[7][8]、人工智能控制[9]和一致性控制[10-13]等。

相比于其它控制，一致性理论着重考虑编队内无人机位置和速度等参数的一致性，整个系统的一致性、稳定性较好。文献[10][11]将二阶一致性理论应用到无人机编队控制中。文献[12]将鲁棒控制加入到了一致性理论中，增强了编队的抗干扰能力。

二阶一致性算法的直接控制量为无人机的加速度，其目标加速度可能在短时间内断崖式变化，无人机作为一个物理系统，这样的加速度变化不利于单个无人机的控制与跟踪。本文引入三阶一致性算法，其直接控制量为无人机的加加速度，可以保证无人机的目标加速度平滑变化以更好地完成编队控制。受限于技术发展与成本考虑，目前小型四旋翼无人机的稳定性并不高，续航短，且低空飞行环境复杂，易受干扰，因此单架无人机在任务中失事的可能性比较高，而上述这些研究都没有考虑到编队内无人机失事情况下的应对策略。本文提出了变结构一致性控制算法，并给出了不同无人机失事情况下的编队通讯结构变化规则，极大地提高了无人机编队的可靠性。

2 四旋翼无人机运动模型

四旋翼无人机坐标示如图1所示。

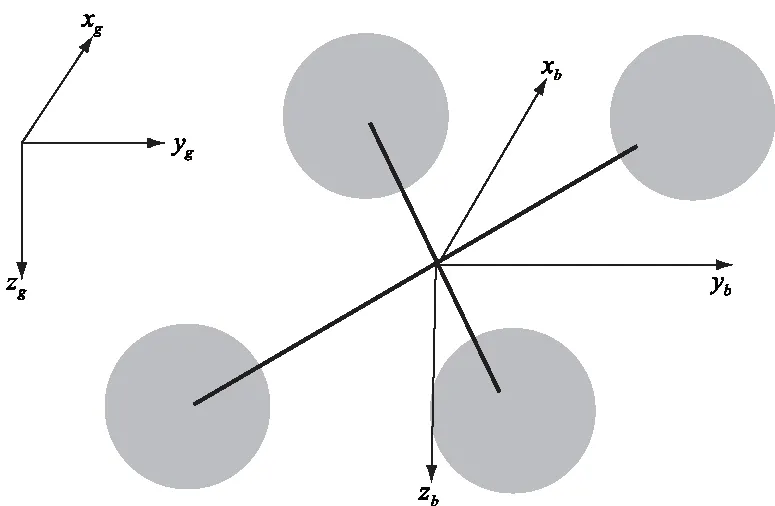
图1 四旋翼无人机坐标示意图

为描述单个四旋翼无人机的运动状态，主要需要定义三个坐标系，即机体坐标系、地面坐标系和长机坐标系。同时定义无人机的姿态，即三个欧拉角：θ，φ，ψ。

机体坐标系b：以无人机的质心为坐标原点，以飞机对称平面内平行于机身周线并指向飞行器前方的轴为X轴，以垂直于飞机对称平面并指向飞行器右方的轴为Y轴，Z轴在飞机对称面内垂直于XOY平面，指向飞行器下方。用于描述飞行器的姿态等信息。

地面坐标系g：以地面选定点为坐标原点。XOY平面平行于地面，两轴方向根据需要进行指定且正交，Z轴则垂直于XOY平面垂直向下。

为方便描述编队内无人机的相对位置，本文定义长机坐标系：坐标原点为编队长机质心，X轴为长机机头方向在水平面的投影，Z轴垂直地面向上，Y轴与X和Z轴成右手直角坐标系。由此可见，长机坐标系下，长机坐标始终为(0，0，0)，而编队内其它无人机的坐标即为其相对于长机的位置。在编队形状保持不变时，编队内无人机在长机坐标系下的目标坐标应保持不变，方便后续观察编队控制效果。

φ为滚转角，为机体坐标系Z轴与通过机体X轴的铅锤面的夹角。θ为俯仰角，是机体坐标系与水平面的夹角。ψ为偏航角，是机体坐标系的X轴在水平面上的投影与地面坐标系的X轴之间的夹角。

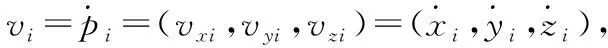
3 基于图论的无人机编队通讯拓扑结构

本文编队结构主要基于图论来展开，本小节将简要介绍一下图论内容。一个有向图(记为G)由节点集合(V(G))、边集合(E(G))、关联函数(φ(G))组成，可记为图G=。

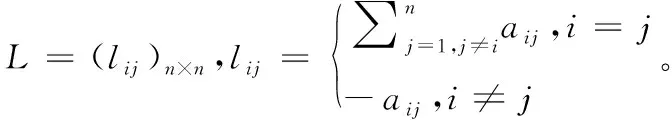
文献[10][11]均采用的无领航的通讯拓扑结构，结构更为紧凑，但不便于给定整个编队的路径。本文使用有领航的通讯结构，同时考虑到通讯网络的简洁性，除长机外每架无人机仅接受一架无人机的信息。为方便描述以及后续某无人机失事情况下进行变通讯拓扑结构，本文把编队内无人机进行分级，第一级为整个编队的长机，仅有一架，记为u1；第二级无人机接收长机的信息，有b2架，记为u21，u22，…u2b2；第三级无人机接收第二级无人机其中一架的信息，有b3架，记为u31，u32，…u3b3；以此类推，编队共有m级无人机，易知：1+b2+b3+…+bm=n。

下面以一个六架无人机的编队为例。如图2所示。

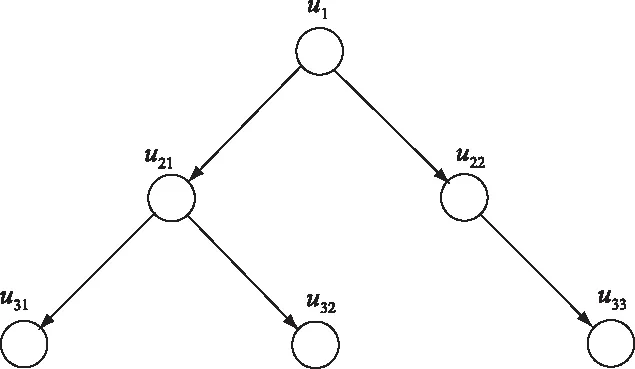
图2 无人机编队通讯结构示意图

4 基于三阶一致性的变结构无人机编队控制器

4.1 三阶一致性编队控制器

编队一致性控制器主要针对除长机外的所有僚机，长机运动状态和路径可根据需要自行给出。

三阶一致性控制器的控制量为无人机的加加速度，控制方程如下：

γ2(vi(t)-vj(t))+γ3(ai(t)-aj(t))]

(1)

为能够在保证系统稳定的情况下取γ1，γ2，γ3的值，需定义矩阵

根据文献[13]推导证明，三阶一致性稳定的条件为矩阵Γ的特征值有且仅有3个为0，且其余特征值实部为负。

采用梯形离散积分得到下一时刻所需的加速度、速度和位置控制信息

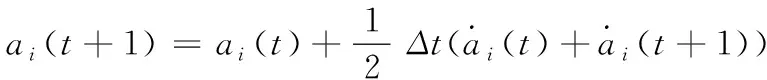
(2)

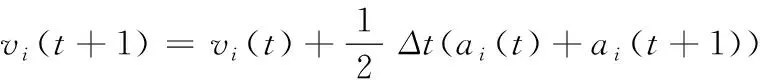
(3)

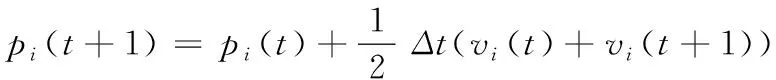
(4)

同时，需要控制从机的航向角与其上一级长机一致，即

(5)

4.2 变结构编队控制器

本文在编队内某架无人机突然失事或大幅度偏离编队时进行编队变通讯拓扑结构的设计。假设编队内共有n架、m级无人机，变结构规则如下：

a) 若失事无人机为第m级，编队内其它无人机通讯拓扑结构不变。

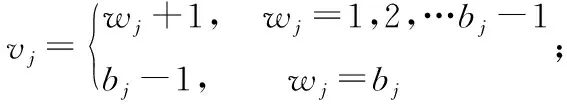
c) 若失事无人机为整个编队的长机，则将无人机u21变为整个编队的长机，第二级中其它无人机接收新长机的信息。

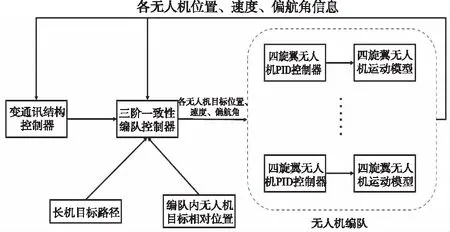
图3 变结构编队控制系统结构图

一般来说，在编队中无人机数量不十分多的情况下，可以提前规划好所有可能的编队结构，即编队通讯图可以用一个集合来表示，记为G={G1，G2，…，Gk}，表示该编队一共有k种可能的通讯结构，编队飞行途中，可以根据实际情况选择不同的通讯结构，以修改对应的邻接矩阵和拉普拉斯矩阵。

5 仿真验证与分析

为验证控制器效果，本文使用Matlab/Simulink进行仿真验证。仿真使用如图2所示的六架无人机的结构，邻接矩阵中a21=a31=a42=a52=a63=1，编队一致性控制参数γ1=2，γ2=4，γ3=6，采样时间为0.1秒，通讯延时为0.2秒。在40秒时无人机u22突然失事。编队通讯结构G={G1，G2，G3，G4}，其中G1为如图2所示的结构，G2，G3，G4为考虑到编队内无人机失事情况下进行的通讯结构的改变，如图4所示。无人机初始相对位置及目标相对位置如表1所示。

表1 从机与长机初始相对位置与目标相对位置

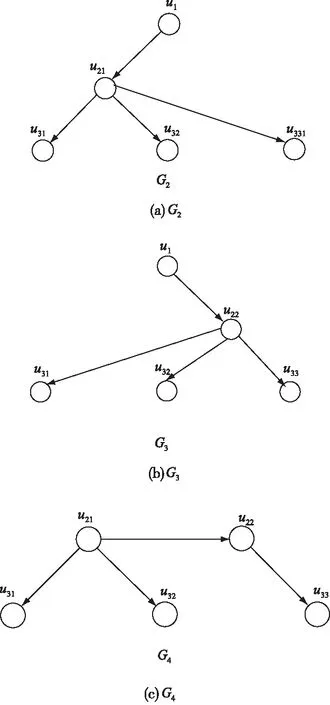
图4 变结构无人机编队通讯结构

图5和图6分别为二阶无变结构控制器和三阶变结构控制器长机坐标系下各从机位置误差图，可以看到在初始相对位置与目标相对位置相差比较大的情况下，其中X方向最大初始误差达到了23米，三阶算法的整个编队稳定时间为17秒，而二阶算法的稳定时间为21秒，且二阶算法的震荡次数明显比三阶多。此种较为理想的情况下两种算法的稳态误差在10-8m量级，基本可以忽略不计，符合编队控制应用要求。而在编队内无人机突然失事的情况下，无变结构控制下接受该架失事无人机信息的无人机即u33明显偏离编队很多，而变结构情况下，u33在很小的波动后位置误差又重新变为0。可以看出，变结构控制器能够很好地应对编队内无人机失事的情况，极大地提高无人机编队的稳定性和可靠性。

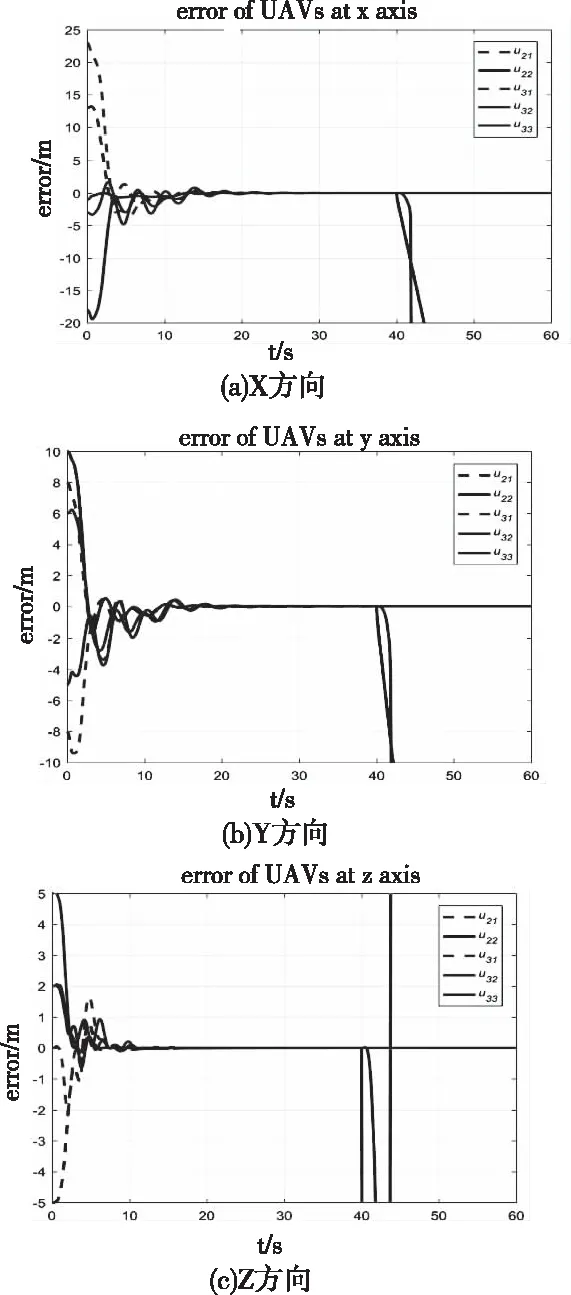
图5 二阶无变结构各无人机位置误差响应图

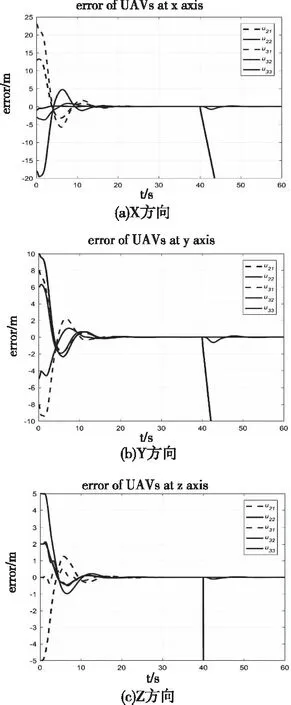
图6 三阶变结构各无人机位置误差响应图

6 结论

本文针对四旋翼无人机编队控制问题，提出了一种变结构三阶一致性控制方法。相对于二阶一致性算法，三阶一致性算法加速度变化平滑，更利于无人机的控制与跟踪，能够显著提高编队控制效果。加入变结构通讯网络，能够有效应对编队内无人机在任务过程中失事的情况。仿真结果表明，多无人机在三阶一致性控制器下能够很快地形成指定编队形状，同时变通讯结构能够极大地提高编队的稳定性和可靠性。