一种非线性动态自适应惯性权重PSO算法

王生亮，刘根友

(1. 中国科学院测量与地球物理研究所，湖北 武汉 430077；2. 中国科学院大学地球与行星科学学院，北京 100049)

1 引言

粒子群优化算法(Particle Swarm Optimization，PSO)是由美国著名学者Kennedy博士和Eberhart博士于1995年通过模拟鸟群集体行为提出的一种集群智能算法，用来寻找问题最优解的随机优化方法[1，2]。由于该算法具有操作简单、收敛速度快、可调参数少等优点，在目标规划、极值优化、图像处理、大地测量、模糊控制等众多领域都得到了广泛应用[3-7]。PSO算法通常可以调整的参数主要有种群大小、最大搜索空间与速度、最大迭代次数、惯性权重、学习因子等。随着深入研究发现，标准PSO算法在进化后期所有粒子速度快速降低，进化停滞不动，存在早熟收敛、易于陷入局部极值等缺陷[8]。其中，惯性权重是最重要的参数之一，算法的执行效果很大程度上取决于惯性权重的选取，其控制着PSO算法的探索和开发能力。采用较大的惯性权重有较强的空间探索能力，即算法的全局搜索能力强，而局部搜索能力弱；较小的惯性权重有较强的开发能力，即算法的局部搜索能力增强，而空间搜索的能力减弱[9]。针对以上缺点，众多学者对惯性权重的选取提出许多改进的策略，如Shi和Eberhart依据种群进化进程及粒子飞行情况对PSO算法的惯性权重进行线性动态调整(Linearly Decreasing Inertia Weight，LDIW)，以平衡搜索的全局性和收敛速度[8，10]。文献[11]和[12]指出线性递减惯性权重中的全局搜索和局部搜索的比例没有变化，对于高维复杂函数的全局搜索和精细局部搜索时间不够，分别设计了指数递减惯性权重(Exponential Decreasing Inertia Weight，EDIW)和余弦递减惯性权重(Cosine Decreasing Inertia Weight，CDIW)，两种策略均能增加迭代初期的全局搜索能力和迭代后期的局部搜索能力。以上现有的方法均在不同程度上提高了标准PSO算法的性能，但并未考虑进化过程中种群粒子整体的适应度值变化与惯性权重的关系，在复杂高维函数优化过程中依然容易陷入局部最优。

为满足PSO算法在进化前期主要对搜索空间进行探索以期尽快达到较优区域，并在进化后期主要对较优区域进行开发的要求，提出种群进化离散度的概念，结合Sigmoid函数，给出一种非线性动态自适应惯性权重因子(Dynamic Adaptive Inertia Weights，DAIW)计算公式。该公式计算简单，能有效提高PSO算法对全局探索和局部开发的能力。仿真实例通过5个标准测试函数将DAIW策略与LDIW、EDIW、CDIW策略的PSO算法进行了对比，验证了该算法的有效性。

2 标准粒子群优化算法

粒子群算法将群体中的个体看作在D维搜索空间中没有质量和体积的粒子，每个粒子有自己的位置x和速度v，在解空间中通过适应度评价函数f(x)不断向自身历史最佳位置pbest和全领域历史最佳位置gbest聚集，实现对候选解的进化。粒子群算法特有的记忆功能使其可以动态跟踪当前搜索情况并调整其搜索策略。粒子群进化过程为

(1)

(2)

式(2)中，γ是粒子的最大速度vmax与最大搜索空间xmax的比例系数；当某维变量的位置或者速度超过边界范围时，采用边界吸收策略，即粒子在下次迭代时落在搜索空间边界上。

标准PSO算法的计算流程如图1所示。

图1 标准PSO算法流程图

算法步骤如下：

1) 初始化规模为m的种群中各个粒子的位置和速度。

2) 计算每个粒子的适应度。

3) 更新每个粒子自身历史最佳位置pbest和全领域历史最佳位置gbest。

4) 按公式(1)更新粒子的速度和位置。若粒子速度和位置超过边界，进行越界处理。

5) 判断算法是否满足终止条件，如果满足则输出最优解并结束，不满足则转到2)继续。迭代终止条件一般选为最大迭代次数Tmax或种群搜索到的最优位置满足预定最小适应阈值。

3 改进的粒子群优化算法

3.1 传统的时变惯性权重PSO算法

惯性权重ω是PSO算法中调整全局搜索与局部搜索的最重要的参数，表达了当前粒子搜索速度对于后续粒子速度的影响程度，从而影响粒子的全局和局部搜索性能。采用固定惯性权重ω取值较大时，全局搜索能力强，可以提升算法收敛速度；取值较小时，局部搜索能力较强，可以提高算法细致寻优能力。

Shi[8，10]于1999年提出采用线性动态递减时变惯性权重策略(LDIW)来达到收敛速度和局部寻优能力之间的平衡，其惯性权重因子为

(3)

其中，ωmax、ωmin为最大、最小惯性权重，一般分别取0.9和0.4，t表示当前迭代次数，Tmax表示最大进化代数。

文献[11]、[12]分别提出的指数递减惯性权重(EDIW)和余弦递减惯性权重(CDIW)因子，分别为

(4)

(5)

式(4)、(5)中各变量含义与式(3)相同。

3.2 改进的动态自适应惯性权重PSO算法

在PSO算法初期，粒子种群中的个体模式集中在适应度值较低的个体上，粒子速度的更新主要由w×v所决定的，若采用较低的惯性权重，种群很难在整个空间“探索”。进化后期，个体模式朝高适应度的个体集中，此时粒子的速度也快速降低，若一直采用低惯性权重，种群的“开发”能力有限，存在早熟收敛，无法跳出局部极值。因此，设计动态自适应惯性权重因子的基本思想是应满足在算法进化前期主要对搜索空间进行探索以期尽快达到较优区域；在迭代后期主要对较优区域进行开发以期尽快找到最优解[13]。

为描述种群进化整体适应度值的变化，给出了进化离散度的定义，将第t代种群与第(t-1)代种群的适应度值标准差之比值定义为进化离散度k(t)：

(6)

在神经网络中常用Sigmoid函数来构造神经元激活函数，其定义为

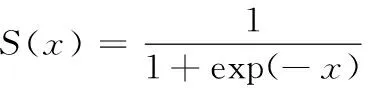
(7)

图2给出了Sigmoid函数图像，为连续光滑且严格单调曲线，以(0，0.5)中心对称，其值域范围限制在(0，1)之间，在x超出[-10，10]的范围后，函数值基本上没有变化。该函数在线性与非线性之间表现出良好的平衡[14]，是一个非常良好的阈值函数，在机器学习、人工智能领域广泛应用。

图2 Sigmoid函数图像

联合进化离散度k(t)和Sigmoid函数，给出一种称之为非线性动态自适应惯性权重因子(DAIW)计算公式，即

(8)

式(8)中，ωmax、ωmin、t、Tmax含义同式(3)，k(t)为种群进化离散度参数，b为阻尼因子，一般取值为[0, 1]。

当ω∈[0.4, 0.9]，Tmax=500时，图3(a)、(b)给出了PSO算法5种不同动态惯性权重因子策略LDIW 、EDIW、 CDIW、DAIW(b=0.2)、DAIW(b=0.5)的变化对比曲线。

图3 不同动态惯性权重因子策略随进化过程变化曲线

从PSO算法的数学模型可以看出，进化过程是粒子多样性逐渐丧失的过程，参数k(t)反映了种群粒子在进化过程中的离散程度变化。在进化前期种群多样性好，相邻两代进化前后离散程度相似，因此k(t)的波动范围较小，即动态自适应惯性权重因子(DAIW)相对平稳递减。在进化后期由于粒子不断对全局最优值的追踪迫使种群表现出强烈的趋同性，因此k(t)对种群的离散程度变化较为敏感，此时动态自适应惯性权重因子(DAIW)震荡幅度较大，有效刺激了粒子的局部“开发”能力。另外，图3(a)阻尼因子b较小，惯性权重ω(t)整体变化比较平缓，整体趋势更加接近LDIW策略。图3(b)阻尼因子b较大，惯性权重ω(t)变化比较陡峭，整体趋势更加接近EDIW策略。因此，阻尼因子b可以充分调控ω(t)的平滑程度，针对不同的问题可以合理调整该值的取值大小。综上，提出的动态自适应惯性权重因子即能充分满足进化初期的全局“探索”，也能更进一步提高进化后期的局部“开发”的能力。

4 仿真实验分析

本文选取了5个benchmark性能测试函数进行分析

1)f1(x)：sphere函数

(9)

sphere函数为单峰函数，全局最小值，x*=(0，0，…，0),f(x*)=0，维数D=30，收敛阈值设定为10-3。

2)f2(x)：Griewank函数

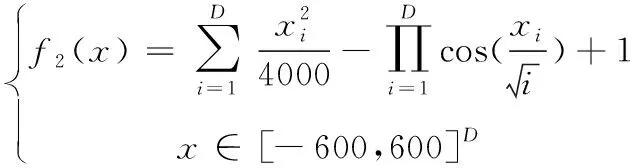
(10)

Griewank函数为不可分离的、可变维数的多峰函数。全局最小值为：x*=(0，…，0)，f(x*)=0，维数D=30，收敛阈值设定为0.10。

3)f3(x)：Rosenbrock函数

(11)

Rosenbrock函数为非凸、病态单峰函数，用来评价优化函数的执行能力，其全局最小值x*=(1，…，1)，f(x*)=0，维数D=30，收敛阈值设定为50。

4)f4(x)：Rastrigin函数

(12)

Rastrigin函数为复杂多峰函数，容易陷入局部最优，全局最小值为：x*=(0，…，0)，f(x*)=0，维数D=30，收敛阈值设定为50。

5)f5(x)：Ackley函数

(13)

Ackley函数全局最小值，x*=(0，0，…，0),f(x*)=0，维数D=30，收敛值设定为0.1。该函数为连续、旋转、不可分离的多峰函数，主要通过一个余弦波形来调整指数函数。此多峰函数有大量的局部最优点。

4.1 不同算法寻优性能分析

为了验证动态自适应惯性权重因子的效率，选取5个测试函数进行测试，PSO算法的参数设置如下：种群大小N=200，最大迭代次数Tmax=500，学习因子c1=c2=2.05，最大速度与最大位置比例因子γ=1，最大惯性权重Wmax=0.9，最小惯性权重Wmin=0.4，阻尼因子b=0.5。使用matlab工具在相同参数情况下分别对LDIW、EDIW、CDIW、DAIW算法运行20次，将各函数适应度值的最优值、最差值、平均值、平均收敛次数、达优率作为评价各算法性能的指标。

从表1-表5中可以看出，提出的算法DAIW的平均收敛值和达优率均明显优于其他3种算法，EDIW和CDIW算法在多数测试函数上的平均收敛值均在不同程度上优于LDIW，与文献[11]和[12]结论相一致。

表1 Sphere函数实验结果

表2 Griewank函数实验结果

表3 Rosenbrock函数实验结果

表5 Ackley函数实验结果

DAIW算法的平均收敛代数，即收敛速度在单峰函数Sphere、Rosenbrock函数为最优水平，在多峰复杂函数Griewank、Rastrigin、Ackley函数上LDIW算法表现更优，DAIW 、CDIW算法获得次优平均收敛速度，EDIW算法在所有的测试函数上的收敛速度都表现最差。

4.2 不同算法种群多样性分析

为进一步更好地说明提出的算法的有效性，分析种群粒子在进化过程中的多样性。种群多样性测度可以准确地评价种群是否正在进行探索或开发[15，16]，具体计算公式如下

(14)

图4 不同PSO算法的种群多样性测度值比较

从图4可以看出，线性递减惯性权重(LDIW)算法的种群多样性测度在进化过程中以最快的速度降低，不利于前期足够的空间探索，易陷入局部最优，因此算法的平均收敛值和达优率最差。指数递减惯性权重(EDIW)算法在种群进化过程中较长的时间内一直保持非常高的水平，即种群的空间探索时间足够长，有效地提高了算法的前期探索能力，但过长的探索时间导致了算法收敛速度的下降。而提出的非线性动态自适应惯性权重(DAIW)算法种群多样性在进化前期保持在较高的水平，充分满足粒子在整个空间进行探索；随后缓慢地降低，即在较小的空间内进行开发，即该算法克服了LDIW算法种群粒子多样性丧失太快和EDIW算法探索时间太长而导致收敛速度下降的缺陷。

5 结束语

通过对线性递减惯性权重、指数递减惯性权重、余弦递减惯性权重粒子群优化算法进行分析，指出了其收敛速度慢和存在早熟问题的原因。结合自定义的进化离散度参数与Sigmoid函数，设计了一种非线性动态自适应惯性权重因子粒子群算法，该算法实现简单，能有效地满足进化前期对搜索空间进行探索；在进化后期对较优区域进行开发的要求，避免早熟收敛，尽快找到最优解或近优解。仿真实验对比分析了4种惯性权重策略PSO算法的性能，结果表明改进的惯性权重因子比传统的时变惯性权重具有更好的寻优能力。