一种新的BOC(n，n)无模糊跟踪算法

孙希延，周 青，纪元法，付文涛

(桂林电子科技大学信息与通信学院，广西 桂林 541004)

1 引言

为了解决全球卫星导航系统(Global Navigation Satellite System，GNSS)的频段拥挤问题，Jhon W.Betz提出了BOC调制方式[1]。BOC调制方式的优点在于可以将中心点的频谱分裂到两端，能够有效地利用频带资源。但其相关函数存在多个副峰，将导致对信号的误捕和误锁。

为了解决跟踪过程中的误锁问题，国内外研究人员提出了一些无模糊跟踪方法：①类BPSK-like方法[2，3]，通过带通滤波器处理BOC信号，相关后得到无模糊的类似BPSK信号的相关函数，虽兼容性强，但牺牲了 BOC 信号跟踪精度高，抗多径能力强的优势，性能较差；②重构方法[4，5，6]，通过设计辅助信号或者重构本地码与输入信号做相关运算达到去模糊效果，文献[4]中，新合成的相关函数仍有小的副峰，导致跟踪性能不是很好；③驻留-跳跃(Bump and jump，BJ)[7]方法，通过使用额外的相关器包括超前和滞后相关器来检查环路是否正确锁定在主峰上。若没有锁定在主峰，跟踪精度降低。但在信噪比较低的情况下，检测会出现较高的虚警概率。

针对以上算法存在的不足，本文提出一种新的BOC(n，n)无模糊跟踪算法。该算法通过对本地BOC码重构运算得到仅有一条尖锐主峰的相关函数，不仅可以解决信号跟踪问题中的模糊问题，还具有良好的跟踪性能。

2 BOC信号调制模型及自相关

传统BPSK调制的表达式如下

(1)

其中，P是信号能量，d(t)代表导航数据，c(t)代表伪随机噪声码。

BOC调制即在式(1)基础上，再调制一个方波副载波，根据文献[8]，BOC(n，n)信号的时域模型可以表示为

SBOC(n，n)(t)=SBPSK(t)*SC(t)

(2)

方波副载波SC(t)数学模型为

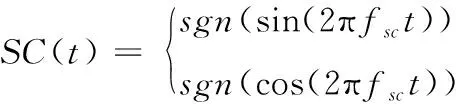
(3)

其中，BOC(n，n)以f0=1.023MHz为基准频率，则c(t)的频率fc=nf0，周期为Tc=1/fc。fsc是副载波频率且fsc=nf0，sgn(sin(2πfsct))代表正弦副载波，sgn(cos(2πfsct))代表余弦副载波。因此正弦BOC调制和余弦BOC调制的数学表达式如下：

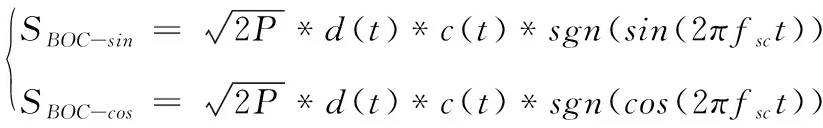
(4)

正余弦BOC调制的示意图如图1和图2。

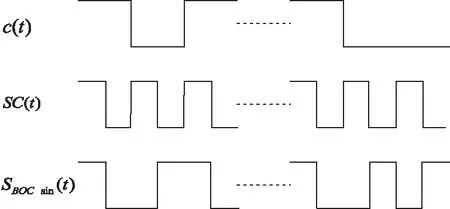
图1 正弦BOC调制

图2 余弦BOC调制

图3给出了BPSK和BOC(n，n)的自相关函数，从图中可知，与BPSK相比，BOC(n，n)的自相关函数具有多个边锋，这将会导致模糊性问题。

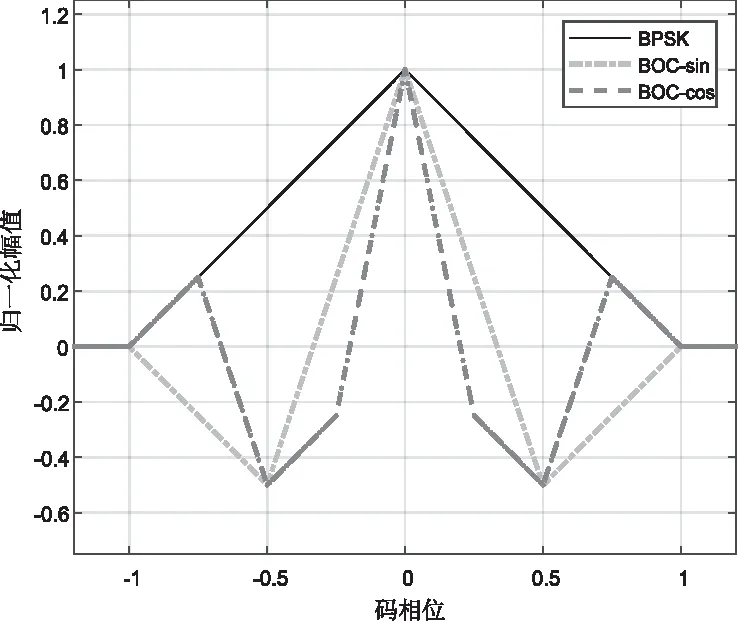
图3 BOC(n，n)的自相关函数

3 提出新的无模糊跟踪算法

3.1 新算法的重构规则

本文引入一个变量为τ，中心为0，宽度为L，幅值为1的单位三角函数tri0(τ/L)，根据图2所示BOC(n，n)自相关函数的特性，BOC-sin(n，n)和BOC-cos(n，n)的自相关函数的表达式分别表示为

(5)

(6)

在上述表达式的基础上，将RBOC-sin(τ)和RBOC-cos(τ)取模，再经过如式(7)和式(8)所示的重构规则，即可得到消除其它边锋的新的自相关函数Rpro-sin(τ)和Rpro-cos(τ)，重构规则如下

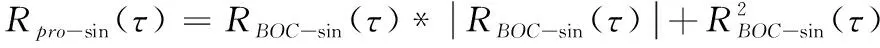
(7)

(8)

式(7)和式(8)的重构算法可以统为

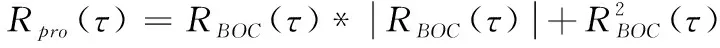
(9)

由式(7)和式(8)所示的重构规则，可以得到如图4和图5所示的重构过程。

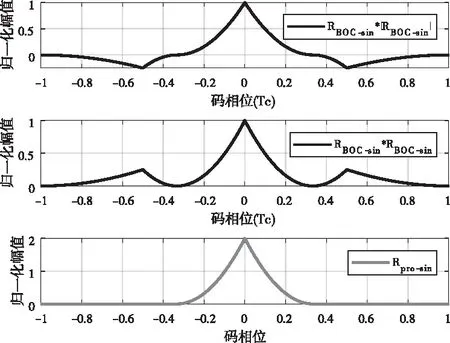
图4 BOC-sin(n，n)的重构

图5 BOC-cos(n，n)的重构

从图4和图5可以看出，重构后的自相关函数消除了边锋并具有较窄的主峰，且主峰更加尖锐。这使得在跟踪环路中不会造成假锁，所以本文提出的算法可以更好的应用于BOC(n，n)信号的跟踪处理。

3.2 算法实现框图

图6为新算法的跟踪环路实现框图，结构和流程与传统的码跟踪环一致，不同的是本算法的本地码为接收信号对应的BOC码，鉴相公式也不同，具体将在鉴相曲线部分进行分析。图4中，E、L分别表示超前和滞后。具体实现过程为：接收信号首先对I、Q两路本地载波进行载波剥离，同时将码生成器复制的C/A码做超前、滞后处理；然后经相关运算后，用鉴相器鉴别相位差异；最后通过环路滤波和数字控制振荡器调节本地码相位，完成对BOC的无模糊跟踪。

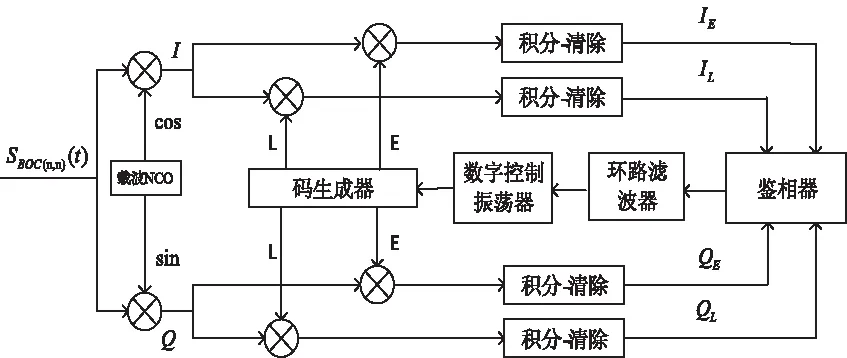
图6 本文算法跟踪环路实现框图

4 性能分析

4.1 无模糊分析

本文通过仿真BPSK-like、ASPeCT、SCPC和本文提出算法的相关函数来验证去模糊性有效性和通用性[9]，如图7和图8所示，以BOC (1，1)为例，设定采样频率为40.92MHz，中频频率为30MHz，SNR=0，码相位为600采样点。仿真结果表明，本文方法的相关峰值是BPSK-like、ASPeCT和SCPC的两倍，且主峰较窄，BOC-sin(1，1)能够完全消除副峰，BOC-cos(1，1)也仅有两个较小的副峰，相比较其它几种算法，本文提出的算法去模糊性最好，这将直接关系到BOC跟踪的抗多径和抗噪声性能。

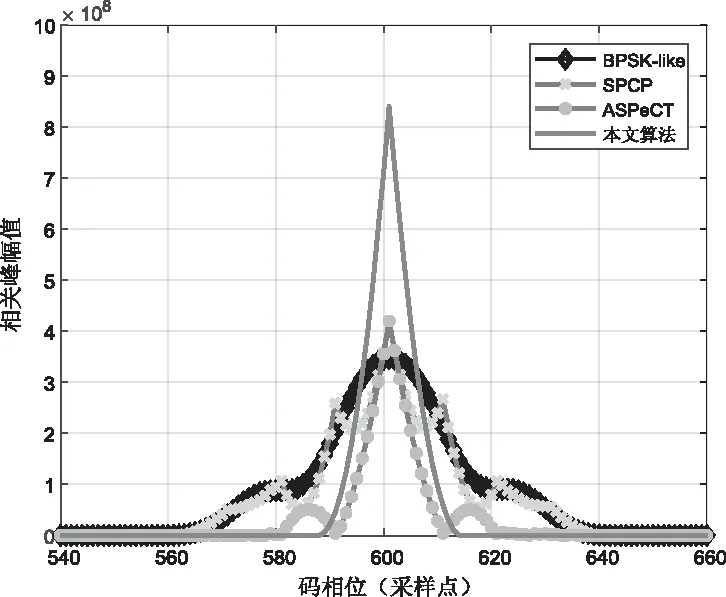
图7 BOC-sin(1，1)的二维捕获结果

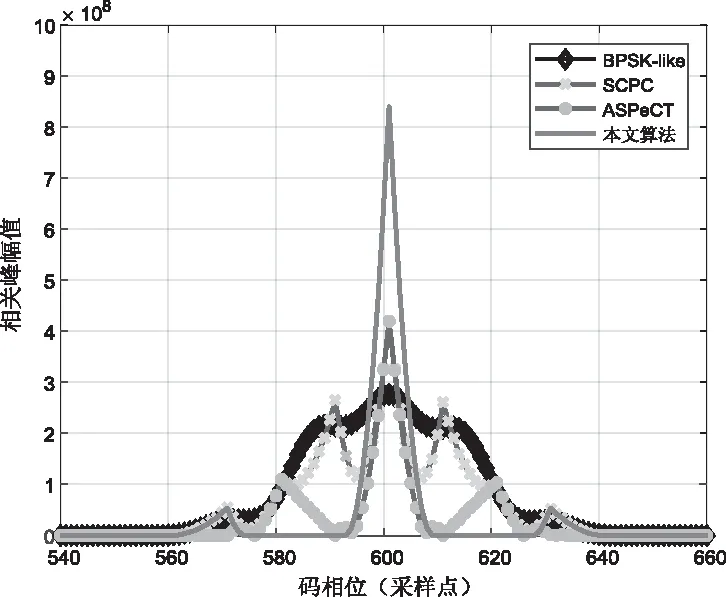
图8 BOC-cos(1，1)的二维捕获结果

4.2 鉴相曲线

在跟踪环路中，若不考虑多径和干扰，接收到的中频信号可以表示为[10]

*cos(2πfIFt+θ0)+n(t)

(10)

其中，fIF是中率，θ0是初始相位，τ是输入信号的码相位延迟。n(t)是功率谱密度为N0的噪声[11]，其它字母的含义在第二部分已介绍，这里不再赘述。

载波剥离后，I、Q支路的同向和正交分量可以表示为

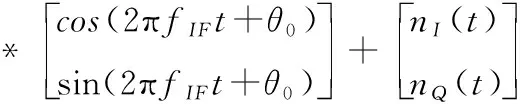
(11)

其中，nI(t)和nQ(t)服从高斯分布[12]，均值为0且功率谱密度为N0。

I、Q支路信号与超前滞后本地码相关后，经过积分清除，得

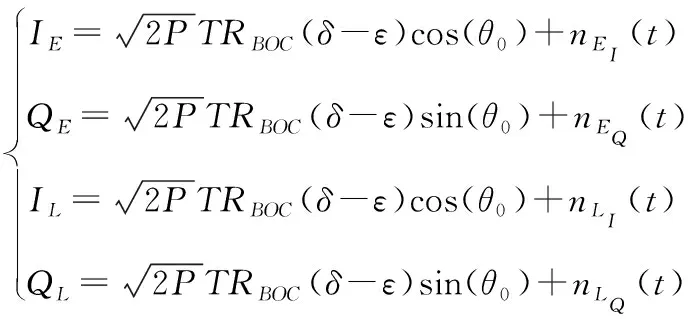
(12)

其中，RBOC代表BOC的自相关，T是积分时间，δ是码延迟，ε是相关器间隔，nEI、nEQ、nLI、nLQ均为服从高斯分布的噪声项。

结合式(9)以及式(12)，可得经过重构规则后的新的鉴相公式如下

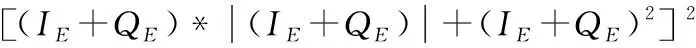
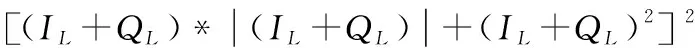
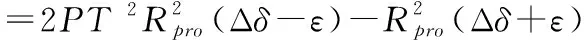
(13)

图9和图10是四种算法对BOC(n，n)的鉴相曲线，相关器间隔为0.1Tc。仿真结果显示，对于BOC-sin(n，n)和BOC-cos(n，n)，传统EMLP的鉴相曲线均有2个误锁点。ASPeCT、SCPC和本文算法都能够消除误锁点，但是相对于SCPC，本文算法能在-0.1Tc～0.1Tc的线性区间 有较大斜率，与跟踪精度密切相关[13]，而且鉴相曲线也更加稳定。

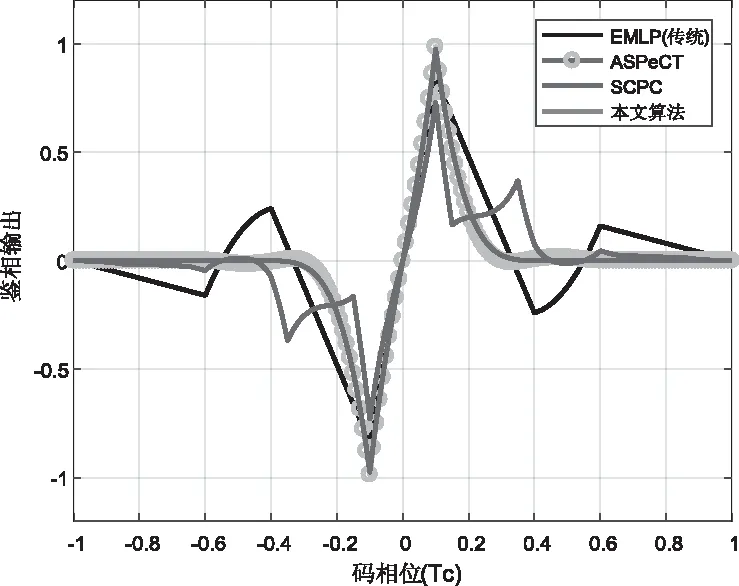
图9 BOC-sin(n，n)的鉴相曲线

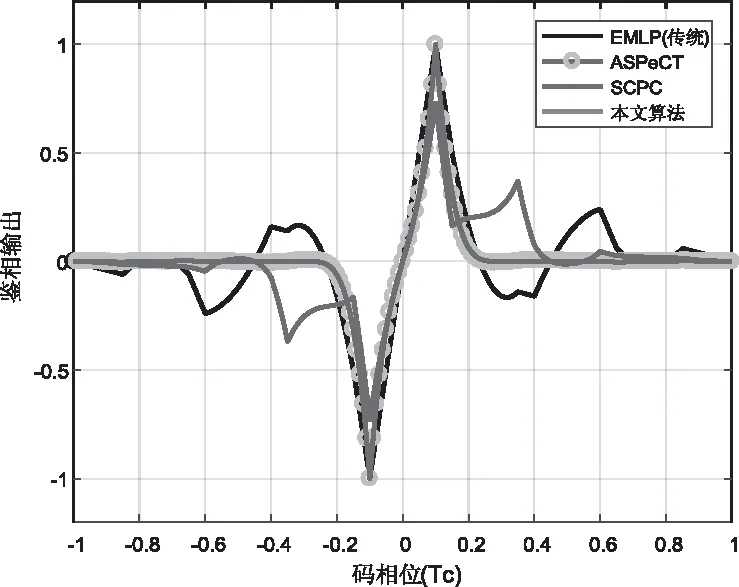
图10 BOC-cos(n，n)的鉴相曲线

4.3 抗噪声性能

热噪声是衡量抗噪声性能的重要指标，码相位测量误差均方差的公式如下[14]

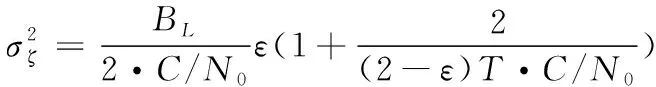
(14)

其中，BL是环路噪声带宽，C/N0是载噪比，ε是相关器间隔，T是相干积分时间。

设置BL=1Hz，T=1ms，ε=0.1Tc，仿真不同载噪比情况下，传统EMLP、ASPeCT、SCPC和本文算法的码相位测量误差均方差，如图11和图12所示。仿真结果表明，当载噪比大于15dBHz时，四种方法的抗噪声性能趋于一致，当载噪比达到15dBHz时，跟踪误差稳定在0.05Tc。对于BOC-sin(n，n)，本文算法的抗噪声性能明显优于其它三种方法，对于BOC-cos (n，n)，本文算法、传统EMLP以及ASPeCT方法的抗噪声性能非常接近，但是两种情况下，SCPC算法的误差都是最大的，因此，本文算法的抗噪声性能是最好的。

图11 BOC-sin(n，n)的码相位测量误差均方差

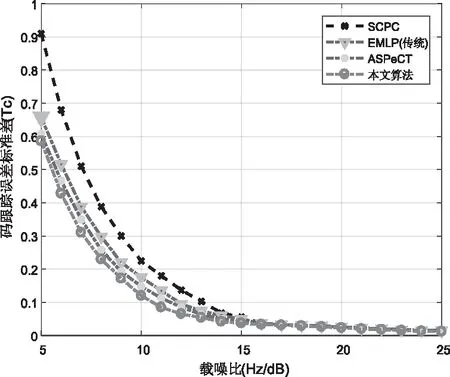
图12 BOC-cos (n，n)的码相位测量误差均方差

4.4 抗多径性能

多径也是跟踪模糊的主要误差源，多径误差包络(Multipath Error Envelope，MEE)曲线是评估跟踪环路抗多径性能的指标[15，16，17]。本文以一条多径的现象为例，相应于式(10)的接收信号，对相关器所输出的再经相干积分后的自相关函数表达为

RM(τ)=Rpro(τ)+βRpro(τ-τ0)cosφ0

(15)

其中，β、τ0和φ0分别代表多径信号相对于直射信号的幅值、延时和相位。

设置相关器间隔为0.1Tc，图13和图14显示了传统EMLP、ASPeCT、SCPC和本文算法的多径包络情况。仿真表明，无论是BOC-sin(n，n)还是BOC-cos(n，n)信号，传统EMLP和SCPC算法的多径误差都较大，且本文算法的多径抑制效果略优于ASPeCT算法，抗多径性能在四种方法中最好。

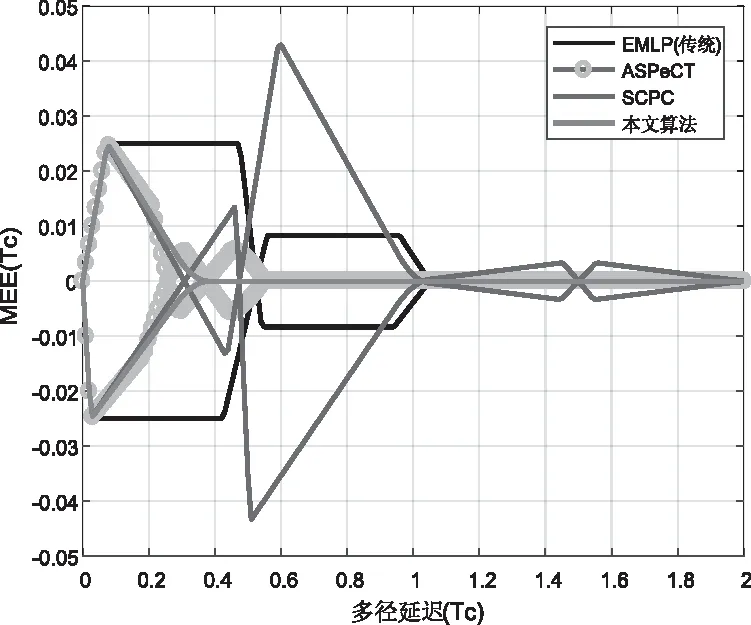
图13 BOC-sin(n，n)的多径误差包络

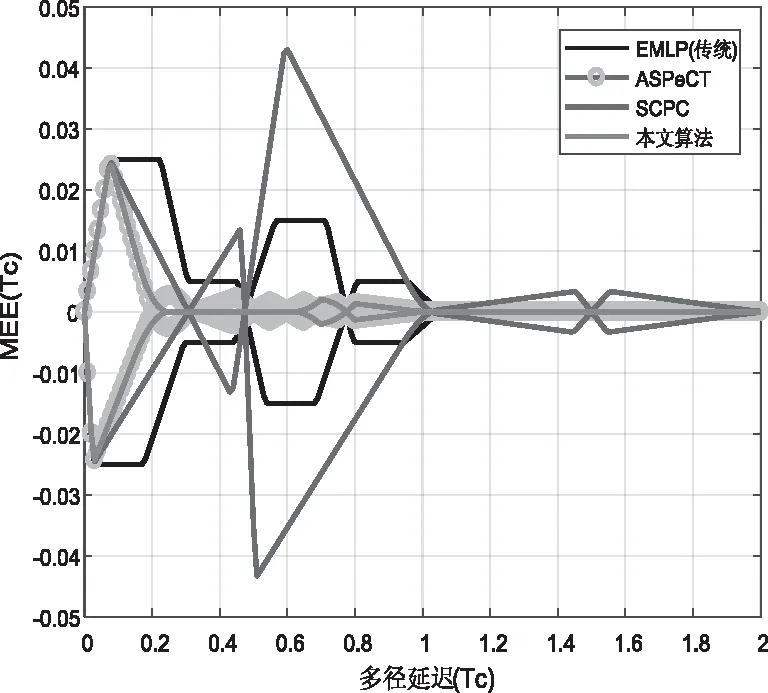
图14 BOC-cos(n，n)的多径误差包络

5 总结

本文提出一种新的无模糊跟踪算法，通过研究可得出如下结论：

1)本文方法通过重构规则合成新的相关函数，消除了副峰且保持了窄相关，基于此相关函数的延迟锁相环实现了对BOC(n，n)信号的跟踪。

2)该算法不需要设计辅助信号，只需对BOC(n，n)信号做自相关处理后进行简单的运算，操作简便，实现复杂度低。

3)通过仿真和分析可以看出：和传统EMLP、ASPeCT和SCPC算法相比，本文算法主峰尖锐且峰值较高，去模糊性最好；在鉴相曲线输出结果中，能够消除误锁点且有较大斜率，鉴相曲线也更加稳定；该算法的抗噪声性能和多径抑制效果也明显优于其它三种算法。

本文提出的算法可应用于GPS、Galileo与我国北斗系统中的接收机中，对于其它BOC族群的无模糊跟踪方法具有借鉴意义。