减振器环形阀片弯曲变形的有限元分析

陈 双，陈剑桥，李政原，孙晓帮

(辽宁工业大学汽车与交通工程学院，辽宁 锦州 121001)

1 引言

筒式减振器在汽车中使用广泛，其阀系结构参数极大影响了减振器的阻尼特性。对于阀系采用纯阀片结构的减振器，环形阀片的计算一直是减振器参数化模型的难点。能否精确计算环形阀片变形，直接影响仿真模型中示功特性与速度特性的准确性，因此如何能够准确的计算出阀片变形对提高减振器的工作性能起着至关重要的作用[1-2]。文献[3]中李双义等人基于薄板大挠度变形理论研究了的单阀片厚度对减振器的特性的影响，文献[4]中周长城等人探究了多阀片的等效厚度对减振器特性的影响，文献[5]中]陈轶杰等人基于薄板变形小挠度理论的研究多阀片等效厚度对减振器的特性分析，但无论基于薄板变形的大挠度变形理论分析还是基于薄板变形小挠度变形理论分析计算量都很大，为减振器的示功特性数学建模带来了困难。

本文将基于有限元理论对减振器阀系阀片弯曲变形进行分析，首先通过减振器示功机试验台得到较大范围的与阀片变形量相对应的压强数据，然后利用CATIA软件对减振器阀系阀片进行三维建模并在ANSYS软件中对三维模型进行有限元求解，完成减振器阀片的变形研究，最后通过薄板变形的小挠度理论对研究结果的正确性进行验证。

2 考虑油液粘温特性的减振器阀系性能试验

2.1 减振器油液粘温特性

温度是液体粘度的重要影响因素之一，温度影响液体粘度的一般规律是随着温度的升高，液体的粘度降低，现已知在温度T0=293K时，此减振器中的油液的粘度为μ0=1.24*10-2N·s/m2，由文献[6]知任意温度下粘度μ与温度T的关系为

μ=μ0e-β(T-T0)

(1)

根据式(1)在MATLAB软件中中绘制油液的粘温特性曲线如图1所示。

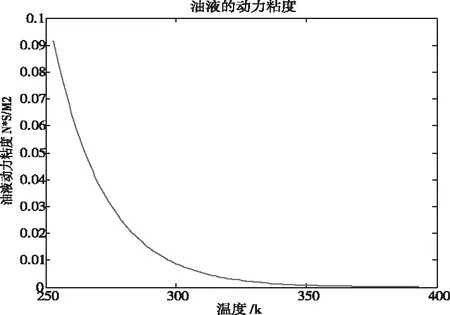
图1 油液的粘温特性

由图1可知，减振器内油液的粘度随温度的升高而降低，当温度超过350K时油液的粘温特性趋近于0，所以减振器在输入相同速度情况下，温度越低时减振器中减振器阀系阀片两端受到的压力也越大，阀片变形量也会变大。

2.2 减振器阀系性能试验

通过恒温箱与示功机对减振器进行试验，为了获得较大范围的与阀片变形量相对应的压强数据，实验时温度定为253K，电流为0A，输入活塞杆的运动速度分别为为0.05m/s，0.15m/s，0.25m/s，0.35m/s，0.45m/s，0.55m/s，实验结果如图4所示。

通过恒温箱与示功机对减振器进行试验，为了获得较大范围的与阀片变形量相对应的压强数据，实验时温度定为253K，电流为0A，输入活塞杆的运动速度分别为为0.05m/s，0.15m/s，0.25m/s，0.35m/s，0.45m/s，0.55m/s，实验结果如图4所示。

图2 减振器示功机 图3 高低温实验箱图

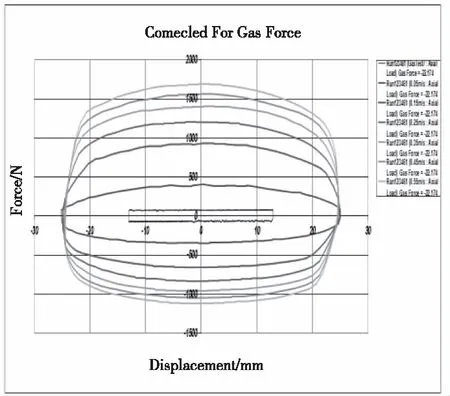
图4 减振器实验数据

由图4可知，当温度为253K，活塞杆运动速度为0.55m/s时，复原阀片两端的最大压强差压差为6.023Mpa，压缩阀片两端的最大压差值为6.376Mpa，所以在ANSYS软件中对三维模型实验载荷时复原阀片两端最大压强差取6.2Mpa，压缩阀阀片两端最大压强差最大取6.4Mpa。

3 减振器阀系阀片三维模型建立

已知减振器环形阀片的材料为硅钢片，其弹性模量E=2.09×1011，泊松比μ=0.3，对减振器的压缩阀与复原阀进行拆解如图5和6所示，测得压缩阀片和复原阀片数据如表1和表2所示。

图5 压缩阀及阀片 图6 复原阀及阀片

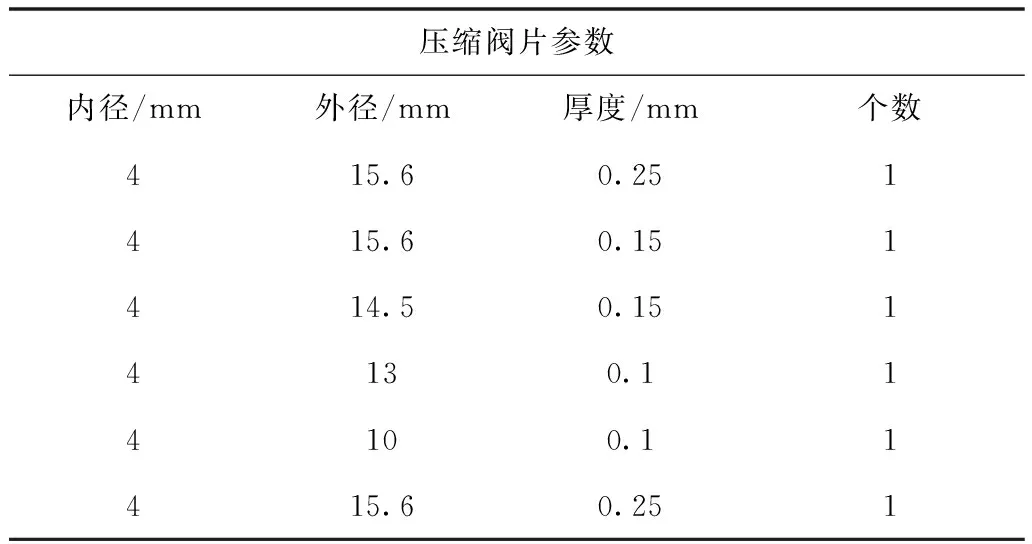
表1 压缩阀阀片参数

表2 复原阀阀片参数

根据表1和表2中的数据计算阀片的当量厚度，并在CATIA中绘制阀片的三维模型如图7和图8所示。

图7 压缩阀片模型 图8 复原阀片模型

阀片叠加的当量厚度计算公式

(2)

其中hd为阀片叠加的当量厚度，h1为第一片阀片的厚度，h2第二片阀片的厚度，hn为第n片阀片的厚度。

4 阀片弯曲变形的有限元分析

有限元分析是指利用数学的近似的方法对真实物理系统进行模拟，利用有限数量的未知量去逼近无限未知量的真实系统。有限元分析问题的本质是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的互连子域组成，对每一单元假定一个合适的较简单的近似解，然后推导求解这个域总的满足条件如结构的平衡条件，从而得到问题的解，有限元不仅计算精度高，而且能适应各种复杂形状，因而成为工程分析的常用手段。

因ANSYS软件作为有限元求解的常用软件有着计算快，精度高等优点，本文选用ANSYS软件对阀片的弯曲变形进行有限元求解，首先将前面建立的复原阀片与压缩阀阀片三维模型导入到ANSYS软件中进行属性添加，有限网格格划分，然后施加约束与载荷，最后完成有限元求解，下面以复原阀阀片为例。

图9 弹性模量与泊松比的添加

收集数据汇总成表格如表3和表4所示。

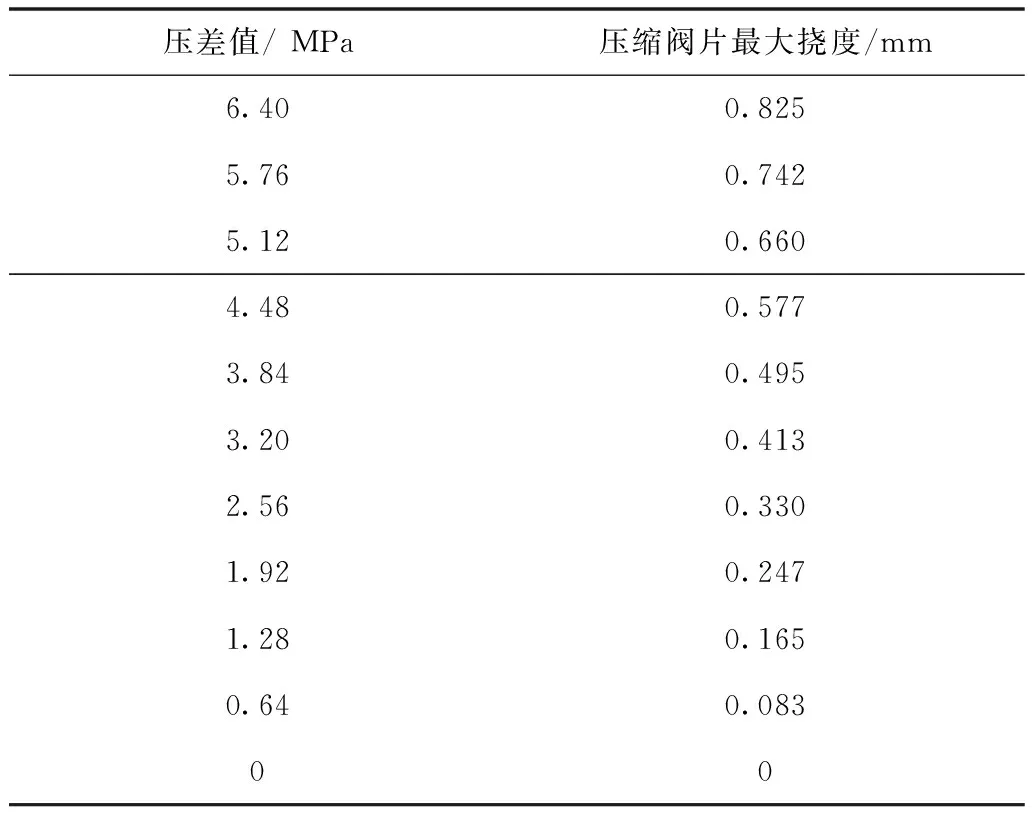
表3 压缩阀阀片变形

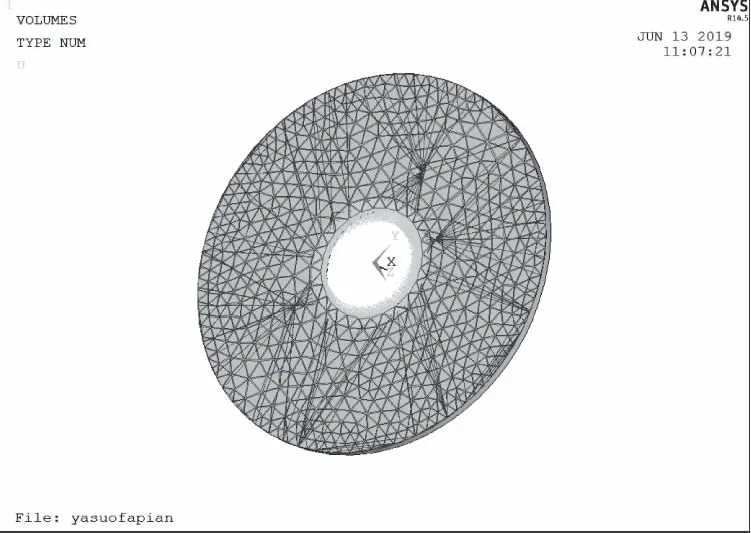
图10 进行有限元网格划分并施加约束

图11 进行有限元求解

图12 有限元求解结果

表4 复原阀阀片变形

根据表3和表4中的数据，在MATLAB软件编写m文件，采用多项式拟合法拟合出阀片变形与两端压差的关系曲线如图13和图14所示。

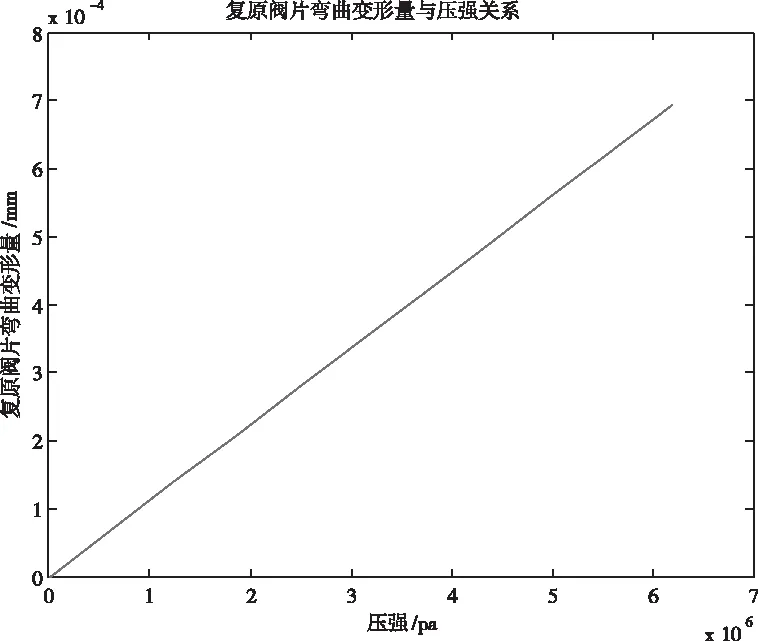
图13 复原阀片变形量与压强关系

图14 压缩阀片变形量与压强关系

复原阀片变形量与两端压强差的拟合公式

χ1=0.1118p1+1.3636×10-4

(3)

压缩阀片变形量与两端压强差的拟合公式

χ2=0.1288p2+1.3636×10-4

(4)

其中χ2，χ1分别为复原阀片与压缩阀片的变形量，p1，p2分别为复原阀片与压缩阀片两端的压强差。

5 有限元分析结果验证

为了验证上一节经过有限元分析所得到的式(3)和(4)的正确性，本文通过薄板变形的小挠度理论得到相同条件下的阀片变形量。

平分板厚度的平面称为板的中面，当板的厚度不大于板中面最小尺寸时的板称为薄板。薄板的中面是一个平面，薄板在垂直于中面的载荷作用下发生弯曲时，中面变形所形成的曲面称为挠度面。中面内点在未变形中面垂直方向的位移称为板的挠度，薄板变形的小挠度理论除了满足弹性力学的基本方程外还应有以下假设：

1)变形前垂直于板中面的直线变形后仍为直线，并垂直于变形后的中面。

2)与中面平行的各面上的正应力与应力相比属于小量。

3)在横向载荷作用下板发生弯曲时，板中面并不伸。

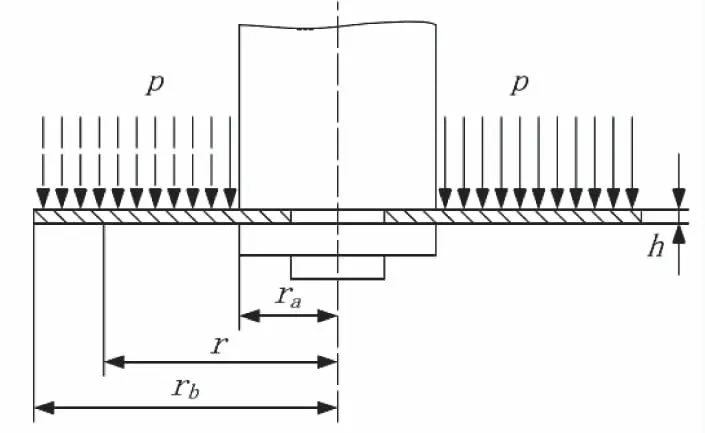
图15 匀布载荷下弹性阀片的受力示意图

其弹性变形的微分方程为

(5)

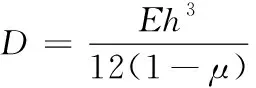
(6)

式中

r-极径

ra-阀片内圆有效半径

rd-阀片外圆有效半径

f-阀片在极径r处的弯曲变形量

h-阀片厚度，当有多个阀片叠加时按照等效厚度计算

E-阀片的弹性模量

μ-泊松比

微分方程的通解为

(7)

微分方程的特解为

(8)

C1，C2，C3，C4由边界条件确定，根据边界条件，阀片内圆为固定约束，外圆为自由约束

外圆：M|r=ra=0;Q|r=ra=0

将待定常数与特解带入到微分方程中，得到阀片在半径r处弯曲变形量的通解

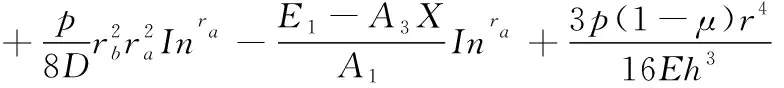
(9)

式中

B2=2(μ+1)；

A3=2ra；

根据上述公式在MATLAB中编写m文件，将表1中的数据带入公式，绘制图像16-17如下。

由图16和图17可知，在压强差较小时，由有限元方法得出的阀片变形量和基于薄板变形小挠度理论得出的阀片变形量基本一致，当压强差较大时，有限元方法得出的阀片变形量略大于基于薄板变形小挠度理论得出的阀片变形量，造成这种结果的主要原因是用限元方法得到插值拟合公式时的拟合误差以及小挠度理论本身的基本假设存在的误差。

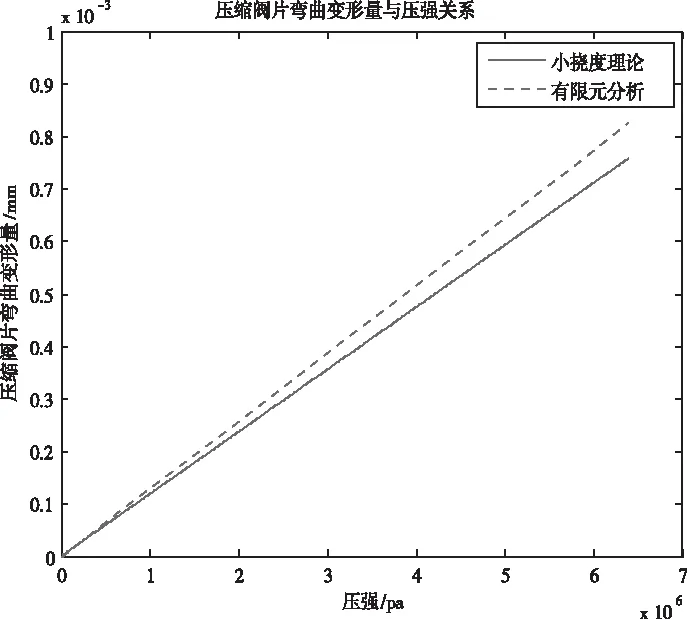
图16 压缩阀片变形量与压强的关系

图17 复原阀片变形量与压强的关系

6 结论

本文基于有限元理论研究了减振器阀片变形量与阀片两端压强的关系，并通过薄板变形小挠度理论验证了其结果的正确性，为减振器阀片变形研究提供了新方法。