带非线性观测器的船舶路径跟踪预测控制
李宗宣,卜仁祥,于镓铭
(大连海事大学航海学院,辽宁 大连 116026)
1 引言
欠驱动船舶路径跟踪是典型的运动控制问题,其主要目的是在不考虑时间限制的情况下,使船跟踪上参考路径[1]。对此,为简化路径跟踪控制的复杂性,Fossen提出一种line-of-sight(LOS)视觉制导方法,将三维位置控制简化为一维艏向控制[2]。但由于路径跟踪存在舵幅与舵速受约束、舵角需优化、模型不确定以及外界干扰等问题,因此对其控制仍具有一定难度。
文献[3]为解决外界干扰和内部模型不确定,设计出基于PID的自抗扰控制器(ADRC)。文献[4]将ADRC与滑模控制相结合,对内部未知项和外界干扰具有良好的抑制作用。文献[5]利用ADRC的核心成分,即扩张状态观测器对外界干扰进行了估计。文献[6]设计出非线性自适应控制器,以应对模型中的未知部分。文献[7]同样利用自适应方法设计自动舵,主要解决波浪干扰问题。文献[8]利用径向基函数神经网络(RBF)技术,对模型未知参数进行逼近。 此外,文献[9] 提出RBF和神经网络观测器,对未知项和船舶速度均进行估计。文献[10]提出一种比RBF更简便的最小学习参数技术(MLP),以减小对未知项逼近的计算量。文献[11]利用干扰观测器,对外界干扰进行估计。文献[12]提出增量反馈滑模控制,避免了外界干扰和未知参数的影响。除了解决模型未知项和干扰问题,对控制输入的约束问题也是不能忽视的,否则所设计的控制律将不能理想地使系统稳定,甚至适得其反。考虑于此,文献[11]在控制律中加入辅助系统,以避免输入限制问题。 文献[13]通过在迭代滑模中引入具有极值限制性的非线性双曲正切函数,约束了最终的控制输入范围。当今人们不仅要求输入的幅值大小受限制,而且希望获得具有变化小并光滑的更优控制输入,以减小能量损耗。则与以上方案相比,模型预测控制(MPC)在处理约束和优化问题上别具一格,更为有效[14], 文献[15]提出线性MPC和非线性MPC, 并通过对比仿真,验证了两种控制器解决输入约束的有效性。文献[16]为解决轨迹跟踪中的控制输入及控制增量约束问题,设计线性MPC控制器,其简单但也对较大的外界干扰过于敏感。 大多数MPC需要基于与实际船舶模型相符的预测模型,来进行预测未来状态的。而实际中,精确的预测模型是很难获得的,这增加了难度。
参考以上文献,对于模型未知项和外界干扰的解决方案已有诸多成果,而对输入约束和优化的考虑较少[3-5]。有鉴于此,本文利用MPC处理舵角优化、舵幅与舵速约束问题。将与实际船模更为相符的分离型模型(MMG)作为预测模型,而且利用非线性观测器对预测模型中的总未知项进行反馈补偿,以处理MPC预测模型与实际模型之间存在偏差的问题[15-16]。最终对比仿真结果验证了所提控制算法的有效性。
2 船舶模型和控制目标
2.1 MMG模型
船舶位置与其相应的运动参数如图1。

图1 船舶平面位置与运动参数
其中,φ是艏向角;u是对地纵向速度,v是对地横向速度,r是转艏角速度,V=(u2+v2)1/2是对地合速度,β=arctan(v/u) 是漂角,δ是舵角。考虑风浪流干扰的船舶MMG模型可表示为[12]
(1)
式中,m是船舶质量,mx和my是附加质量,XH、YH和NH是裸船体力(矩),XP、YP和NP是螺旋桨力(矩),φc和Vc分别是流的流向和流速,XW、YW和NW是风力(矩),XWave、YWave和NWave是浪力(矩),Izz是船舶绕竖直轴的惯性矩,Jzz是附加惯性矩,XR、YR和NR是舵力(矩),其计算如下
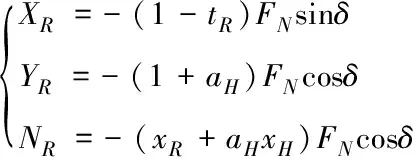
(2)
式中,tR是舵阻力减额份数,αH是操舵引起的船体附加横向力与舵横向力的比值,xH是操舵诱导船体横向力作用中心到船舶重心的距离,FN是舵正压力
2.2 控制目标与假设条件
由于路径跟踪不需要考虑纵向位移,只需将横向位移y镇定为0,便可使船跟踪上路径。因此,本文控制目标是给定螺旋桨转速,设计合适的舵角使船跟踪上设计的路径,即满足横向位移偏差ye=0。在设计控制器过程中,所需要的假设条件如下:
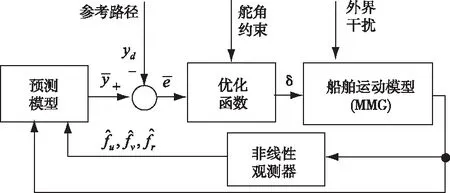
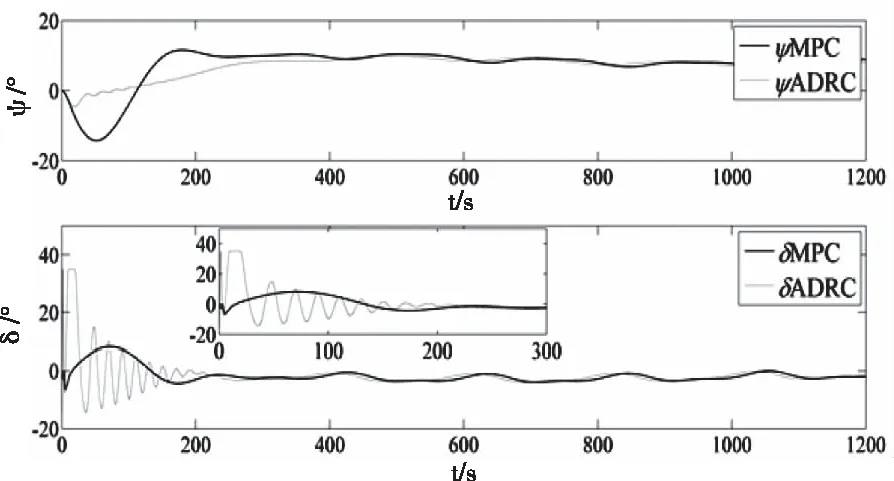
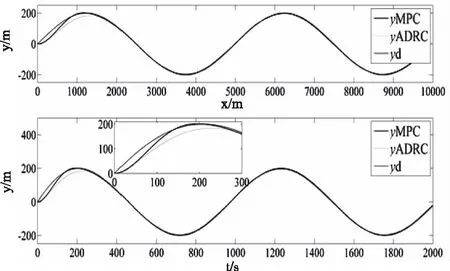
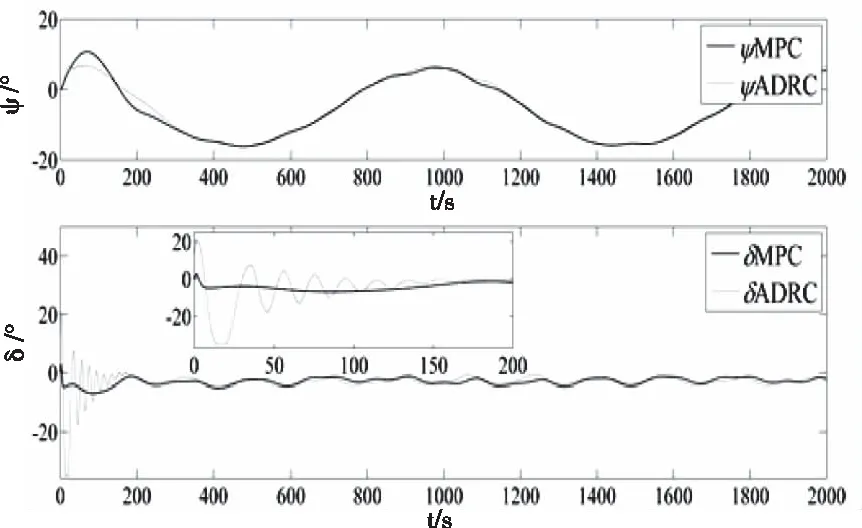
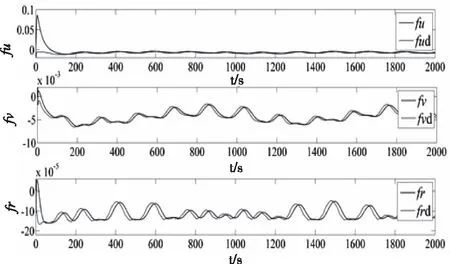
Ⅰ.包含模型不确定项和外界干扰不确定项的总未知项f有界,即|f| Ⅱ.总未知项f的一阶导数有界,且和u、v、r相比都较小。 其中,Ⅰ是系统可控的必要条件。Ⅱ由于海洋环境的变化非突变,因此环境干扰变化速度和船舶运动速度相比较小。 本文将MPC作为路径控制器,利用非线性观测器对预测模型中的总未知项f进行逼近和补偿。控制结构如图2。 图2 控制结构图 本节以MMG模型作为预测模型,设计MPC路径跟踪控制器。首先基于欧拉迭代法对船舶未来状态进行离散和预测[17] (3) (4) (5) (6) 利用当前时刻和未来时刻的路径偏差设计优化函数,并为对舵角进行优化,将其也置于优化函数中,如下 (7) 式中,Q和P均为权重,以调节路径性能和舵角性能之间的平衡关系,Δδ为舵速,Nc为控制时域,且Nc 本节设计非线性观测器,对预测模型中的总未知项fu、fv和fr进行逼近。先以fu为例设计观测器,如下 (8) (9) 式中,η是正系数。对V2求导如下: 根据假设条件Ⅱ,g3可以忽略不计。由于双曲正切函数和线性比例函数相比受到极值限制,因此选择合适的正参数ku1>ku2可以使g2和(-u)异号,即当(-u)<0时g2大于0,此时,式(8)中的第2项将大于0,则u将会增加至u>fu,从而g1和g2都将大于零,则有而当0<(-u)时g2会小于0,式(8)中的第2项也小于0,则u将会减小至u 为验证所提MPC算法的有效性,将本文MPC控制器与文献[4]所提的ADRC方法做对比仿真。仿真对象为原大连海事大学育龙号实习船,其舵角δ约束值为35°,舵速Δδ约束值为3-6°/s。式(1)中的风浪干扰力矩计算如下: 风力XW、YW和NW计算如下[19] (11) 式中,ρα是空气密度,αR是相对风向角,UR是相对风速,Af和As分别是水线以上的正投影面积和侧投影面积,Loα是船舶总长,Cwx(αR)、Cwy(αR)和Cwn(αR)分别是风压力系数。 由于大型万吨级船舶本身可抵消一阶高频波浪影响,故在此仅考虑二阶浪力XWave、YWave和NWave,如下[20] (12) 式中,λ是浪波长,χ是波浪遭遇角,ρ是海水密度,α是波幅,CXw(λ)、CYw(λ)和CNw(λ)分别是波浪漂移力(矩)系数。 1)直线路径: 初始位置(x0,y0)=(0,200m), 参考路径yd=0.外界干扰:风速10m/s,风向20°sin(0.035t)+45°,流速1m/s,流向10°sin(0.005t)+45°, 浪波长83m,波浪遭遇角 φ+135°-20°sin(0.03t)。 图3和4中,yMPC、yADRC、φMPC、φADRC、δMPC和δADRC分别为基于 MPC 和ADRC的路径、艏向和舵角仿真结果。图4中,在时变干扰下,两个控制器均能使船准确的跟踪上参考路径。yMPC跟踪速度快,却也产生了超调,但超调量不到7%,这在实际航行要求之内。图4中,由于时变风浪流干扰的影响,艏向角和舵角都有一定的波动,以抵抗干扰。δMPC不到10°, 而δADRC则达到了满舵值35°,并且δMPC初始振荡幅值和频率都比较小,更为光滑,这说明了所提MPC控制器解决舵幅约束和优化问题的能力。图5可以看出舵速Δδ一直被限制在2°/s。图6描述了所设计的非线性观测器对三个总未知项的逼近能力。 图3 直线路径跟踪 图4 艏向和舵角 图5 舵速 图6 总未知项 2)曲线路径初始状态:(x0,y0)=(0,0).参考路径:yd=200sin(0.0004πx).干扰除流向相反外,其它参数不变。 图7中,两控制器均能使船稳定地跟踪上曲线路径,说明两控制器都可有效地解决模型不确定和外界干扰问题,而yMPC跟踪速度更快。图8中,不仅因为时变干扰,而且由于曲线跟踪本身就需要船舶一直转向打舵,因此艏向角和舵角的变化比直线跟踪较为剧烈。但可以明显的看出δMPC比δADRC变化幅度小,初始振荡时间更短,舵角更光滑。图9和图6一样,验证了非线性观测器估计总未知项的能力。 图7 曲线路径 图8 艏向角和舵角 图9 总未知项 为解决船舶路径跟踪中存在的舵幅与舵速受约束、舵角需优化、模型不确定以及外界干扰等问题,设计MPC控制器,并将舵角置于优化性能指标函数中。将MMG模型作为预测模型,并利用非线性观测器对模型不确定项和外界干扰进行逼近。最后,仿真说明,所设计的MPC控制器使船在风浪流时变干扰下仍能准确地跟踪上参考路径。舵幅和舵速均在限制值内,舵角变化小且初始振荡时间短,更为光滑,这些结果验证了所提控制算法的有效性。3 路径跟踪控制器
3.1 MPC控制器
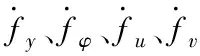
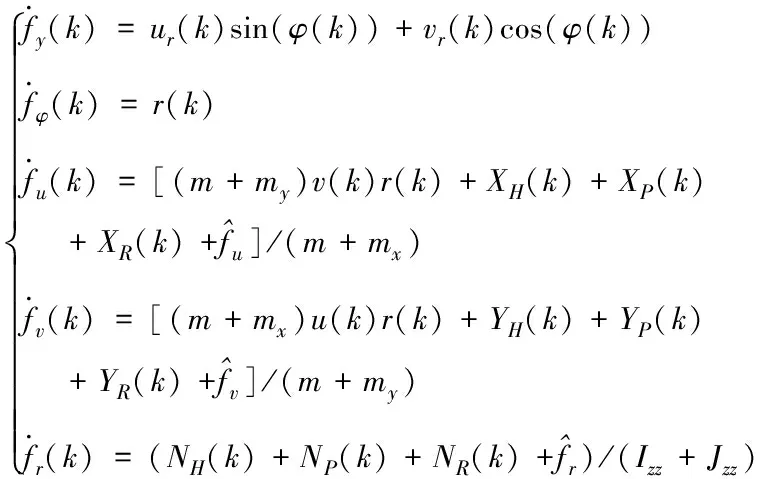


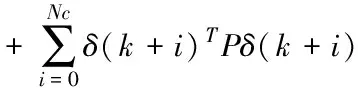
3.2 非线性观测器
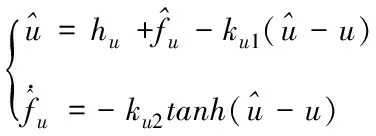
4 仿真分析
4.1 仿真数据
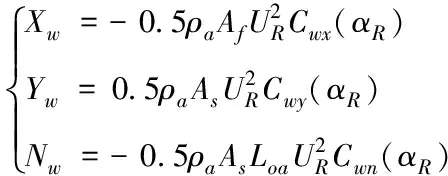

4.2 仿真结果



5 总结

