多目标优化下智能飞行器三维航迹快速规划

丁 超，吴梓杰，张 航

(1.中南大学计算机学院，湖南 长沙410083;2.中南大学自动化学院，湖南 长沙410083)

1 引言

智能飞行器类似于无人机，具有结构精巧，体积较小的优点，而且它更加先进和智能化，非常适合用于军事侦察和对敌设施的破坏。国外学者则更多的关注其路径规划，解决如何将货物送至不同站点的问题[1-2]，而对于智能飞行器所处的复杂环境和飞行器自身性能的问题却缺少研究。在实际应用中，由于智能飞行器自身以及环境复杂性，合理的路径是货物安全、经济、快捷送至目的地的重要保障，故研究智能飞行器的复杂飞行环境和自身性能技术有着极其重要的现实意义。周浪提出了一种运输路径规划解决方法，它构建不同运输路径优化模型，采用遗传算法求解模型，最终仅仅达到了运输成本上的优化[3]；Torabbeigi提出了一种变预处理算法以提高求解模型的速度，但只针对飞行器本身电池能耗问题[4]；Abeywickrama等考虑不同场景及条件对无人机能耗的影响，提出涵盖无人机飞行全过程的能耗模型[5]；Dorling等建立无人机路径规划的混合整数线性模型，综合考虑了飞行器的运输成本和电池能耗[6]；王云常、戴朱祥、李涛提出了一种基于A星算法与人工势场法的无人机路径规划，提高了避障效果，缩短了飞行器搜索时间，主要通过引力场来控制飞行器的飞行方向，从而达到避让大型障碍物的效果[7]；马云红、张恒等提出了一种三维无人机路径规划，同时为了满足无人机俯仰角、偏航角等性能约束，提出了一系列优化算法，最终也只是考虑到了对无人机自身性能的优化[8]；纵观已有成果，常用的方法是将飞行器的路径规划问题简化成一种道路车辆路径规划问题，文献[3-6]要么仅仅考虑飞行器的运输成本，要么只是考虑到了飞行器的能耗问题，没有体现出飞行器空中机动能力和应变能力。文献[7-8]在航迹规划中也没有考虑到飞行环境因素且未将飞行器自身性能等影响要素组合考虑，规划结果并不理想。本文结合智能飞行器的复杂飞行环境和自身性能优化的特点，进一步改进了飞行器三维航迹规划算法，提升效率，减少航程代价，保证飞行器能够通过定位校正到达目的地，完成飞行任务。

2 问题描述与相关假设

2.1 问题描述

智能飞行器受限于系统结构的大小，在飞行过程中会不断产生飞行误差。当飞行误差积累到一定程度，就会偏离目标点，导致飞行任务失败。因此在航迹快速规划时，如何在智能飞行器定位精度的限制下，对定位误差进行校正是一项重要课题。飞行器的定位误差分为垂直飞行误差和水平飞行误差，假设飞行器每前进1m，垂直误差和水平误差将各增加δ个专用单位，当飞行器的垂直飞行误差和水平飞行误差均小于θ个单位时，飞行器可以按照已规划的轨迹飞行，并准确到达目标，从而完成飞行任务。根据飞行区域的特殊地形标识，飞行区域内一些点可以单独对飞行器进行垂直误差或水平校正。校正垂直和水平误差的位置可根据地形在航迹规划前确定(如图1所示， 红色的点为水平误差校正点，蓝色的点为垂直误差校正点，A为出发点，B为目的地)。

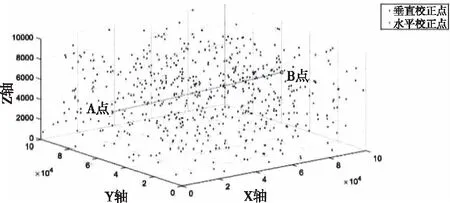
图1 飞行器航迹规划区域示意图

问题一：在对飞行器定位误差进行校正时，当飞行器到达垂直校正点时，飞行器的垂直误差不大于α1个单位，水平误差不大于α2个单位时才能进行垂直误差校正。经过校正，垂直误差变为0，而水平误差保持不变；同理，当飞行器到达水平校正点时，飞行器的垂直误差不大于β1个单位，水平误差不大于β2个单位时才能进行水平误差校正。经过校正，水平误差变为0，而垂直误差不变。问题二：由于飞行器结构和控制系统的限制，飞行器的前进方法无法突然改变，需要通过圆弧路径进行过渡，且转弯的最小半径为200m。问题三：考虑飞行过程中部分校正点校正失效的问题。在飞行中由于某些不可控的因素(如天气、通讯故障等)导致飞行器到达校正点时无法进行理想的误差校正，无法将在该处将误差降低至0。根据给定的信息，飞行器在部分校正点能够成功将某个误差校正为0的概率是80%，如果校正失败，则校正后的剩余误差为min(error，5)个单位(其中error为校正前误差，min为取小函数)。已知信息：出发地A点，飞行器的垂直和水平误差均为0；给出空域校正点的位置及校正信息；相关参数：α1=25，α2=15，β1=20，β2=25，θ=30，δ=0.001

2.2 相关假设

假设飞行器为一质点，飞行器在飞行过程中不会出现突然故障的情况。飞行器的飞行速度对到达校正点校正效果无影响，当垂直误差和水平误差均小于θ个单位时，飞行器仍能够按照规划路径飞行，并且飞行器的最小转弯半径为200m，飞行器在部分校正点能够成功将某个误差校正为0的概率是80%，如果校正失败，则校正后的剩余误差为min(error，5)个单位(其中error为校正前误差，min为取小函数)。

3 优化目标与约束条件确定

飞行器在执行任务的时候需要考虑到多方面的影响要素，本文综合考虑飞行器自身性能约束与飞行器复杂的飞行环境，从飞行器的定位误差校正、机动性能、部分校正点失效等角度建立多约束条件的飞行器三维航迹快速规划模型，设计了飞行器定位误差校正策略和飞行器转弯控制策略。

3.1 飞行器定位误差校正策略

该目标主要研究在准确抵达终点时，飞行器的航迹长度最短，并且经过校正点的次数尽可能少。校正次数与航迹长度存在正相关的关系，即校正次数越多，航迹长度也越长。所以，以航迹最短为求解目标，相对应的校正次数就会越少。目标函数如式(1)所示，n为飞行器误差校正次数。

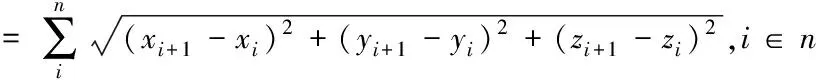
(1)

3.1.1 约束条件一

为保证飞行器能够按照规划航迹飞行，垂直误差和水平误差均应小于θ个单位。即

γp≤θ

(2)

γh≤θ

(3)

γp=(Sii+1-Sii)δ，ii∈np

(4)

γh=(Sjj+1-Sjj)δ，jj∈nh

(5)

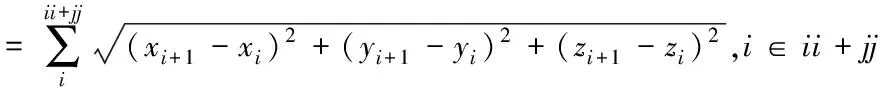
(6)

式中，γp为垂直误差，γh为水平误差。Sii和Sjj分别为飞行器经过垂直误差和水平误差校正后再次飞行的距离。

3.1.2 约束条件二

在对飞行器垂直误差校正时，当飞行器的垂直误差不大于α1个单位，水平误差不大于α2个单位时才能进行垂直误差校正，且经过校正，垂直误差变为0，水平误差不变。垂直校正点的校正误差约束为

(7)

3.1.3 约束条件三

在对飞行器水平误差校正时，当飞行器的垂直误差不大于β1个单位，水平误差不大于β2个单位时才能进行水平误差校正，且经过校正，水平误差变为0，垂直误差不变。水平校正点的校正误差约束为

(8)

3.2 飞行器转弯控制策略

该目标主要研究飞行器在结构和控制系统的控制下，无法及时改变飞行方向，需要通过转弯控制策略进行控制，飞行器的最小转弯半径为200m。本文中提出一种转弯控制策略如图2所示，即在误差校正点首先进行转弯，调整飞行方向，然后沿直线飞行，最终到达下一个目标校正点。

图2 飞行器转弯控制策略图

约束条件除了以上的三种约束条件，还多了一条机动性能约束条件，飞行器的最小转弯半径最小为200m。即在问题一约束条件的基础上，增加了飞行器最小转弯半径的约束，即

Ri≥Rmin=200

(9)

因此，以航迹最短求解目标，增加飞行器的机动轨迹，构建转弯半径约束下的飞行器快速路径规划的目标函数如式(10)所示，n为飞行器误差校正次数。

(10)

式中

li=∅πR/180

(11)

(12)

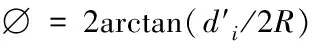
(13)

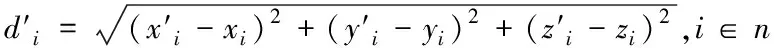
(14)

程序设计中通过对当前规划的路径进行曲率半径估计，判断飞行器航迹飞行段近似曲率半径是否大于等于200m，来确定飞行器是否能在现实环境下飞行。

3.3 部分校正点失效情况

当校正节点集合中存在问题节点时候，为了尽可能保证成功到达的概率下，尽可能减少校正次数和路程，根据分析可知问题节点的特点是校正误差到不了0，只能降到5个单位，也就是在问题一的基础上，考虑校正点失效的概率，即成功校正误差的概率为80%，校正后的误差为0；校正误差失败的概率为20%，校正后的误差为min(error，5)。

(15)

4 算法优化与仿真结果分析

4.1 NSGA2遗传算法优化

本文中研究的约束一定程度上还是比较严格的，而且规模很大，大规模问题结合严格约束的问题，这对算法就提出了两点要求：①初始解产生策略必须可以产生大量的随机的有效解；②新解的产生策略必须保证可以有一定的有效解。又因为要求的两个目标，也就是减少校正次数和减少路程并不完全正相关，尤其在这种复杂的约束的优化问题中，因此考虑采用多目标群智能优化算法，群智能优化算法无论其大小如何，该算法都可以解决问题。从自然界中汲取灵感来开发计算效率高的算法是解决现实世界中最优化问题的一种方法[9]。例如遗传算法，遗传算法是历史上最早提出的基于种群的随机算法之一，主要方法是选择、交叉和变异[10]。这里考虑使用遗传算法改进的智能优化算法NSGA2遗传算法，流程图如图3所示。问题一的模型优化求解使用的是智能优化算法NSGA2遗传算法[11]，与传统的遗传算法上做了一些改进。为了更好的描述NSGA2遗传算法对优化模型进行求解，将优化过程分为了一下几个步骤：Step1：初始化种群，给定种群规模pop、迭代次数Gen、对初始化种群进行非支配快速排序和拥挤度计算。Step2：选择：本文对选择算子进行了一些改进，以Pij式(16)来做轮盘赌法的权值，其中Wmaxl为最大约束参数系数，将点与点之间的距离dij做线性变换，变换后的等式的倒数作为轮盘赌法的权值Pij，当两个校正点的距离足够小时，则对应的权值Pij将会非常大(Pij<1)，因此被选中的概率也就非常大，这正好符合了实际问题对应的航迹长度尽可能的小的要求。Step3：交叉：本文采用多点交叉法，所谓交叉，是指把两个父代个体的部分结构加以替换重组而生成新个体的操作，通过交叉，遗传算法的搜索能力得以飞跃提高[12]。本文采用的交叉主要是通过轮盘赌法选择了一组节点，以这组节点为分界线将两条路径分为四条路径，四条路径两两组合，生成两条新路径。Step4：变异：变异是对基因链上的某个基因按较小概率改变，以此保持个体的多样性，克服早熟现象。变异算子是遗传算法产生新个体的重要操作，是影响算法收敛性能的关键[13]。

(16)

(17)

图3 NSGA2遗传算法流程图

4.2 蒙特卡罗算法

蒙特卡罗算法是一类随机方法的统称。这类方法依赖于使用计算机进行随机实验[14]。这种方法通常用于随机模型或分布中取样或估计与模拟模型相关的特定数量[15]。其工作原理就是随着迭代次数的越来越多，近似结果是最终结果的概率也在增大。由于本文存在两个方向的校正，垂直方向和水平方向，任何出现问题的方向很可能由于这5的单位而导致失联，而这种现象可能下一个校正节点出现，也可能过了很多个校正节点才出现，统计其概率就会比较复杂，因此这里就提出了一种与概率正相关的参数作为优化目标，从而来代替实际概率。因此本文提出了一种新的实现策略，定义概率作为参数，从而成为三个目标优化问题，设初始失败概率为0，初始成功概率为1，在每次都失败的情况下，将会导致那几次无法校正，每次出现失败，就更新概率函数，概率函数如式(18)所示

(18)

式中Psuccessprob是成功概率，Pfailprob是失败概率，这里的失败概率不是真实中的失败概率，只是与失败概率正相关的参数。

4.3 仿真结果分析

4.3.1 数据集预处理

根据从起点A到终点B的航行路线，本文设计了一种圆环形包络面算法，提高模型的求解效率如图4所示。圆环形包络面算法描述如下：首先根据点A和终点B的坐标信息，建立AB空间直线方程；然后以该直线为圆形中心线，以两倍左右的临界校正距离为半径maxr，对该直线圆周内校正点的数据进行搜索包络，保留圆环内的校正点数据，删除剩余的校正点的数据，最终形成了一个圆环形包络面数据集。相对于初始空域校正点集，预处理后的校正点数量大大减少。此外，采用两倍的临界校正距离为筛选半径，可以保证校正点搜索空间充足，不会遗漏最优校正点，从而不会影响最优搜索路径。

(19)

图4 圆环形包络面数据集

4.3.2 结果分析

以下是对问题一中的校正点进行航线规划以后得出的结果，在经过算法的处理后，得到了以下三个候选结果，分别是图5、图6、图7所示。

图5 飞行器规划路径a

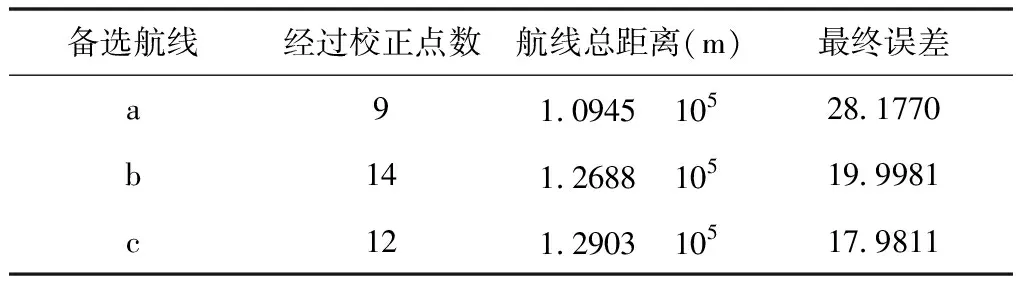
表1 备选结果信息表

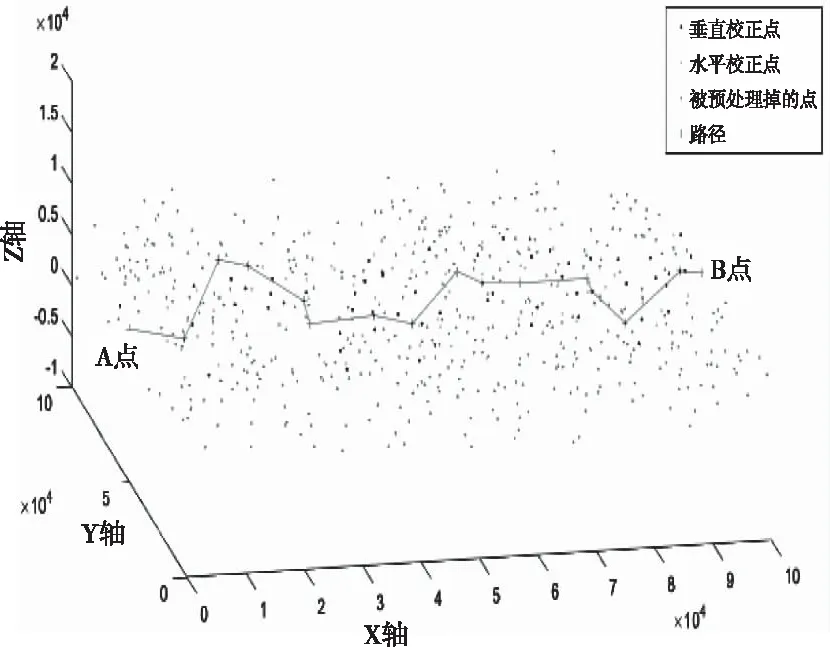
图6 飞行器规划路径b

图7 飞行器规划路径c

针对以上三个的候选航线，为了选出最佳航线，决定利用模糊综合评价法来筛选出最优航线，具体步骤如下所示：Step1：定义以下参数集合：{校正点数u1，航线总距离u2，最终误差u3}；定义评价等级集合：{优秀的v1，良好的v2，及格的v3，不及格的v4}；将权重赋值给每一个参数：{0.05，0.75，0.2}；Step2：可以计算得到三个模糊综合评价矩阵R1，R2，R3，结果如下所示：{航线1：[0.18，0.48，0.315]；评价等级：优秀};{航线2：[0.2，0.56，0.228]；评价等级：良好};{航线3：[0.23，0.64，0.13]；评价等级：良好}

综上所述，选择航线1作为最优航线，在该航线中，经过的校正点数为9个，航线的总距离为1.0945105米，垂直误差为8.490014，水平误差为19.686960，满足约束条件。

航迹路径规划具体结果如表2所示：

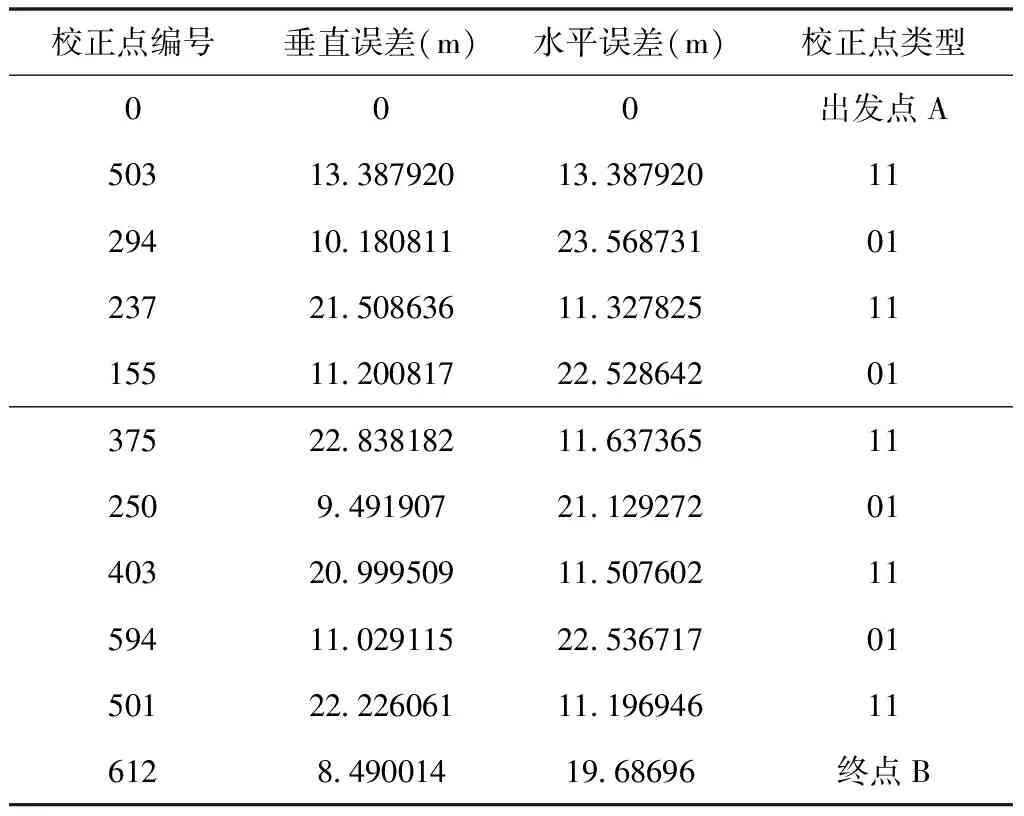
表2 航迹规划结果表a

问题二中的校正点经过算法处理后的结果如图8所示，飞行器的驾驶航线总共经过了9个校正点，其中经过了5个水平校正点和4个垂直校正点，飞行器的航线较为曲折，该航线经过的总距离为1.1524e+05米，相较于AB之间的直线距离1.0046e+05米增加了14780米，符合经过的校正点数尽可能少，经过的航线总距离尽可能短的要求。

图8 飞行器规划路径图

航迹路径规划具体结果如表3所示：

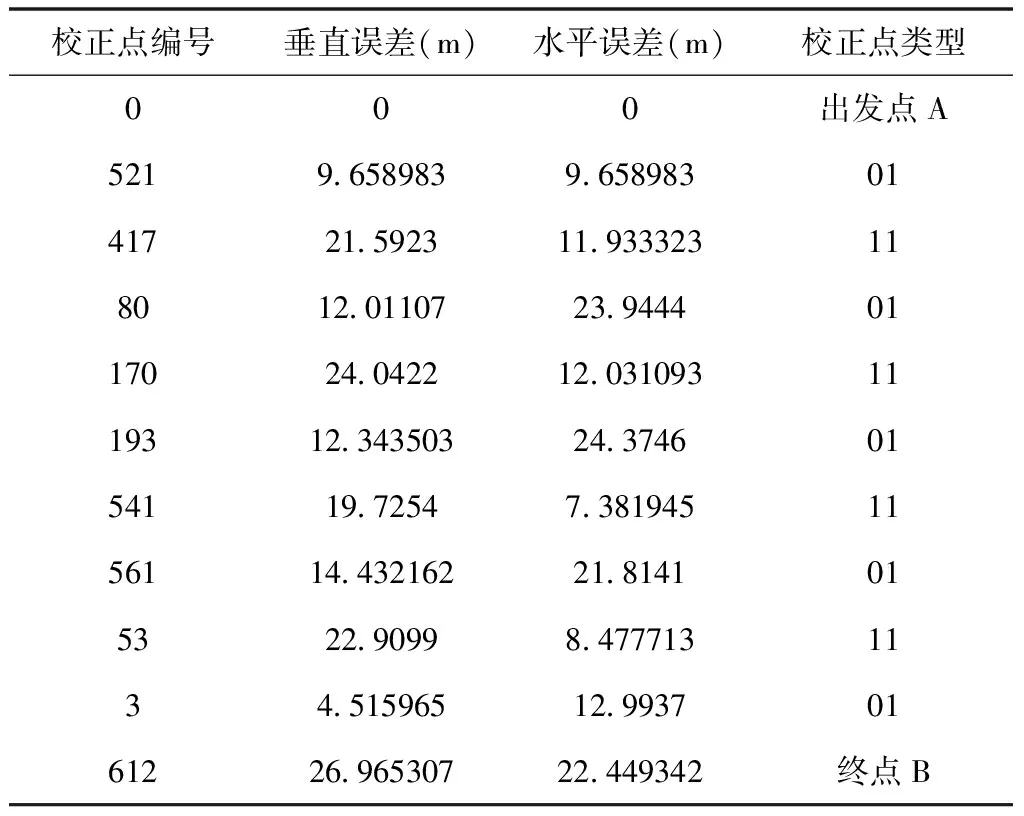
表3 航迹规划结果表b

下面利用校正点失效概率模型重新对该问题进行求解。求解得到的结果如图9所示，该航线飞行的总距离为1.1828105m，相比较于AB点之间的直线距离1.0046105m，航线距离增加了17820m，相对增加了17.7%。飞行器共经过了12个校正点，其中为6个水平校正点和6个垂直校正点。经过的可能出现误差的校正点编号为69，123，302，346，可能出现的无法到达的概率为8.39%。相比于上一种特殊情况，飞行器经过的校正点数量减少了4个，飞行距离缩短了2362m，飞行效率比较高。

图9 校正点失效概率模型飞行器规划路径图

航迹路径规划具体结果如表4所示：

表4 航迹规划结果表c

5 结论

1) 仿真验证表明，圆环形包络面算法可以保证校正点搜索空间充足，不会遗漏最优校正点，降低了计算量，缩短了计算时间。

2) 在出现问题校正点时，本文提出的策略所生成的航迹路线，总体代价较小。在满足最短路程和校正次数最少的基础上，能够完成飞行任务。

3) 本文采用的组合策略充分考虑了飞行器的复杂飞行环境和自身性能，表中数据也表明飞行器可以在复杂的飞行环境中不断的定位误差校正，最后精确地到达目的地，完成飞行任务。