基于自适应匹配的矢量图符号模糊识别仿真

刘 磊，张 燕

(电子科技大学成都学院，四川 成都 611731)

1 引言

随着工程矢量图绘制技术的迅速发展，当前矢量工程图纸已经逐渐普遍，在这些图纸中人们通过丰富多样的特征符号描述，符号识别作为模式识别的关键分支，已经成为了机器理解图纸内容的关键流程，其结果能够广泛使用在图形检索、图纸纠错与三维重建等领域[1]。例如利用工程矢量图符号识别技术将工程电路图有效的读取到数据库中，并通过对电路图进行数据抽取、数据变化和数据重构等操作完成电路图的信息重构，以方便对维修人员进行维修指导和快速培训等任务。

现实中的工程矢量图纸内符号的描述存在多样性，代表同一种类、同一语义甚至同一符号时，具有视觉表达或图元组成上相似但不完全一致现象。这会导致同一种符号在不同的排列上有着不同的语义，或不同的矢量图符号在相同的排放顺序下，存在视觉表达类似的情况，这种情况就会影响到在观察或使用矢量图进行绘制或比照时产生误差，因此需要一种能够精确识别矢量符号的方法，来获取符号的位置与形状。

针对上述问题，提出基于自适应匹配的矢量图符号模糊识别。引入自适应匹配算法，获取符号特征，并转换特征空间，将符号特征与模板进行匹配，获得符号的尺寸，优化符号匹配精度，最后根据自适应匹配方法模糊识别矢量图中的符号。

2 基于自适应匹配的矢量图符号模糊识别

2.1 特征模糊提取

矢量图内的符号模糊性主要来源与符号的多样性描述，现实使用中不同的绘制准则、绘制习惯以及统一绘图者在多次绘制同一种图形时的细节差别，都会使符号最后的视觉表示或图元构成出现差异，本文把这样的现象描述成符号的模糊性。在符号目标与其背景回波的矢量图像内，杂波的出现会导致符号目标距离产生模糊，同时最终干扰对目标符号的识别能力，必须对模糊进行有效的抑制。

拟定{X(n)|n=0，1，…，N-1}代表目标和背景回波组成的矢量图像，在图内拟定一种坐标和宽度都能够产生变化的滑动窗口θ，并通过以往的算法对目标的径向长度与坐标进行计算，在窗口θ与目标符号重叠[2-4]时，使用M来表示其宽度，可以得到杂波水平和度量目标能量的三个量，即杂波平均电平δt，符号平均电平δi与观察窗口平均电平δc，其分别通过以下方程进行计算

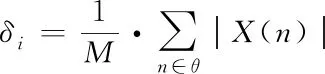
(1)

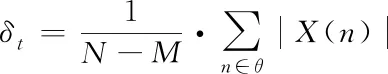
(2)

(3)

式中，只有符号目标和δt的回波能量[3-4]不具有关联，目标特征在进行模糊提取时对信号的预处理需要和符号种类不存在关联，所以能够通过以下公式抑制杂波

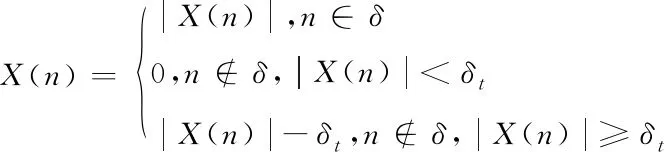
(4)

以此，来剔除因符号目标距离模糊导致的异常目标，引起的相关匹配结果出现误差，博里叶转换的输入信号与幅度在线性位移中不具有任何关联，所以可以用在计算不变特征量上。因此，将{Y(n)n=0，1，…，N-1}转变至频域内完成特征模糊提取，即

(n)=FFT{Y(n)}，n=0，1，…，N-1

(5)

2.2 基于离散度准则的特征空间转换

特征空间转换是符号识别中的重要步骤，即将原始描述空间映射到低维的特征空间里，实现对空间的维数压缩，随后把所有统计内存在关键特征[5-6]的符号储存起来，实现高速、高效的分类。基于离散度准则的特征空间转换，将初始的N维空间转换成C-1维空间，完成特征维数的大幅度压缩。

拟定存在一组已知种类的N维空间样本x1，x2，…，xm，共m种，其中m1种属于第1类样本，拟定成X(1)，mc种属于第C类样本，拟定成X(c)；变换矩阵是W=(wij)N·(C-1)，变换完成之后的特征矢量是

y=WT·x

(6)

其中，y代表C-1维的特征矢量，x为N维矢量，为了搜索变换矩阵W，能够将目标函数J(W)进行最大化处理即

(7)

其中，Sw代表类内离散度，映射了所有类符号目标样本之间的离散度[7]，Sn代表类间离散度，映射所有类样本间的离散度。J(W)的最大化就代表类样本经过一种线性变化，将类间样本距离最大化，同时使类内样本距离最小化。类内离散度Sw拟定成：

(8)

式中

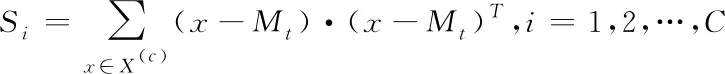
(9)

其中，Mt代表所有类符号目标样本的均值[8]矢量

(10)

类间离散度Sn拟定成：

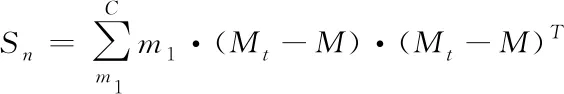
(11)

式中

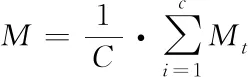
(12)

2.3 基于小样本学习的矢量图符号模板匹配

模板匹配算法适合于矢量图符号这种小样本的匹配，其把目前待分类的符号样本和模板库内的模板进行匹配，获得待分类符号样本和模板之间的距离，为了确保分类器组合的需求，需要把匹配的距离转变成识别可信度。

1)在线模板匹配距离与离线模板匹配距离

因为符号对应点之间的模式距离和模板之间的相似度具有较好的识别效果，本文使用这两种距离用作在线模板匹配与离线模板匹配上，式(15)拟定了两种符号A，B对应点之间的平均欧式距离[9]定义

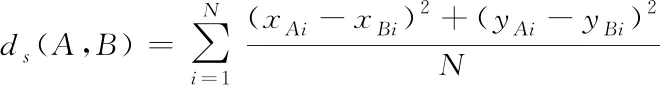
(13)

式中，A，B代表存在N种采样点xAi-xBi与yAi-yBi，其分别是A与B内的第i种点的位置。

由于符号的距离矩阵里存在符号的随机一像素点距离和矢量图黑色像素点最近距离，运算一幅矢量图中某一点至另外一幅矢量图上黑色像素点[10]的最小距离，能够从叠加一幅矢量图至另一幅矢量图的距离矩阵上直接获得，能够加快相似度的运算效率。

2)匹配距离到识别可信度的转换

为了便于模板匹配算法与之后构建的分类器能够顺利融合，把模板匹配获得的距离转化成识别可信度，拟定d1(A，B)=ds(A，B)，d2(A，B)=H(A，B)，首先把匹配距离进行归一化处理即

(14)

式中，dMaxi代表第i种模板匹配[11]算法相应的最大匹配距离，dMini代表第i种模板匹配算法相应的最小匹配距离。

2.4 基于自适应匹配的矢量图符号模糊识别

基于上述的符号分类与模板匹配后，本文给出了基于自适应匹配的矢量图符号识别算法，首先通过匹配交互学习符号样列组建符号库，随后通过匹配到的符号在复杂的图纸内搜索与之相同或类似的符号[11-12]实例，大致流程如下所示：

步骤1：针对原型符号B与待识别图G，对其中的所有基元结构进行提取，组成B与G的集合LSB与LSG。

LSB={lsB，i，i=1，2，…}

LSG={lsG，j，j=1，2，…}

(15)

步骤2：对随机lsB，i∈LSB，计算LSG内的所有局部邻域结构lsB，i和lsG，j的距离D(lsG，j，lsB，i)。

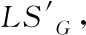
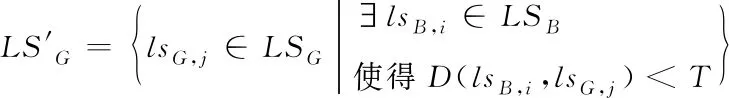
(16)

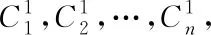
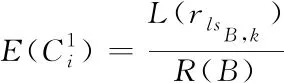
(17)

式中，rlsB，k代表符号内核lsi距离最近的结构的主基元，缩放因子初始化成该主基元尺寸和整体原型符号包围盒半径尺寸的比值。

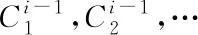
(18)

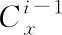
(19)

假如，在计算完成之后，匹配的结果并没有被合并，那么直接将其作为第i步结果内的一类。

3)迭代2)，直至前后两次的匹配结果不会出现变化。

步骤5：挑选候选结果，在步骤4内，匹配结果是C1，C2，…的类通过图内的若干架构形成，通过步骤4与步骤3能够看出，在前Ci内的所有元素都和符号内的某种局部结构相同，并且这些元素空间的距离是非常近的，这就能够认为其代表另一种候选结果，这一步评测该结合在多大几率上覆盖了待识别符号的局部结构，本文经过合并和Ci内各元素相似的待识别符号内的结构得到该类在符号结构集合内的相似子集BCi⊆LSB，即

(20)

假如BCi的元素总量不超过待识别符号的结构集合元素总量的一般，那么评定类Ci只和符号的很小一部分类似，剔除该类，通过挑选后，剩下的所有类就是符号识别的结果。

3 实验结果与分析

本次实验以电路图为实验样本，样本来源于矢量电路图在线编辑器(https：//fangyong2006.iteye.comblog728058)，为全面验证所提方法的矢量图符号识别性能，利用电路图在线编辑器设计两种电路图，分别为带有矩形外框的矢量电路图和无矩形外框的矢量电路图。利用本研究提出的基于自适应匹配的矢量图符号模糊识别方法分别对两个实验样本进行符号识别。

3.1 带有矩形外框的矢量图字符识别效果

本节实验的目的为测试所提方法能否准确识别带有矩形外框的矢量电力图内的字符。由于实验样本矢量电路图内的个别字符存在两层矩形框，增大了识别难度，增强实验结果的可靠性。

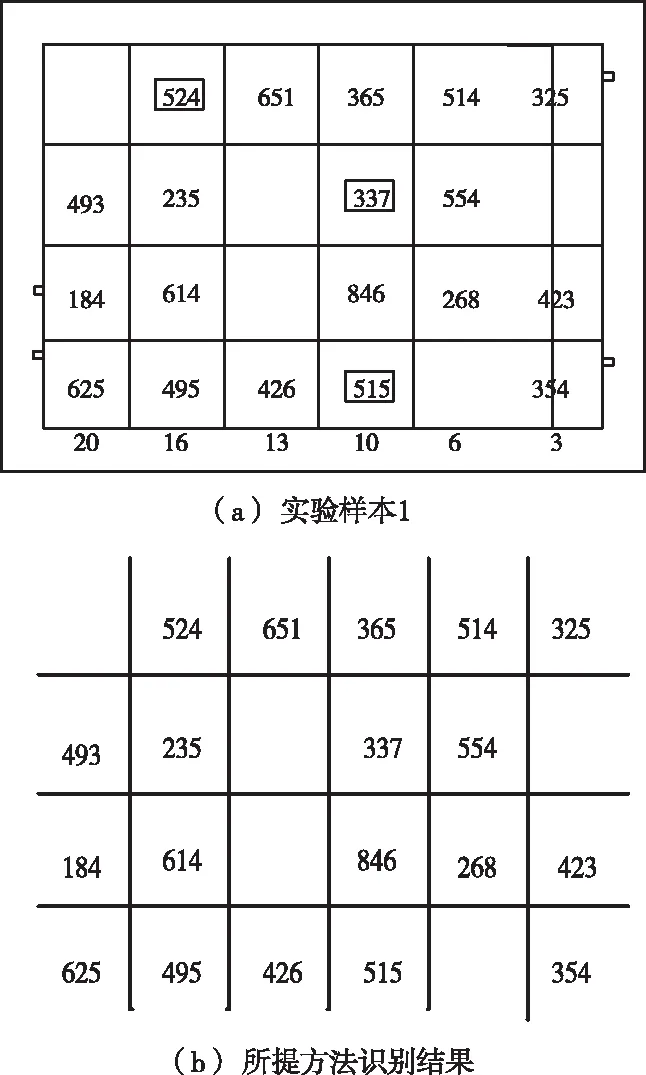
图1 带矩形外框电路图字符识别结果

通过图2能够看出，本文方法能够较为完成的识别出大量矩形块中的字符。这是因为本文方法先通过提取特征后依靠模板与符号样本的坐标位置进行匹配分类，不会因为符号种类多而产生识别缺失问题。

3.2 无矩形外框的矢量图字符识别效果

为进一步测试所提方法的应用有效性，以无矩形外框电路图为实验样本(如图2(b))，具体实验结果如下：

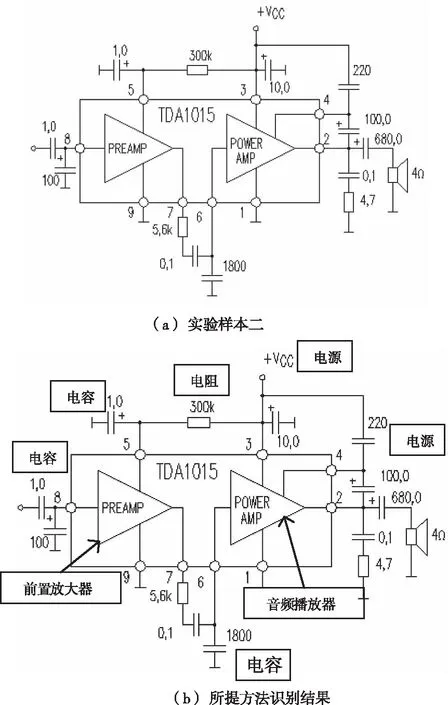
图2 所提方法矢量图电路符号识别结果

通过图2可以看出，在无矩形框的矢量电路图的符号识别中，本文方法能够较为完整的识别出矢量图内的符号。这是因为本文方法在进行模糊识别之前，会对整体的矢量图进行模板匹配，通过这种匹配后的矢量图不会因为边框的剔除，影响到识别结果的精确性。

4 结束语

1)为提高矢量图的实用性与利用率，本文提出基于自适应匹配算法的矢量图符号模糊识别方法。将已知特征待分类符号样本与模板库内模板匹配，并获取样本与模板间的距离，完成矢量图符号识别。且通过实验证明了所提方法识别效果较为理想。

2)但研究方法仍存在以下弊端：在识别矢量图符号时，矢量图内会存在部分冗余痕迹，例如绘图人员无意间的笔画，而该方法并不能识别出这种冗余痕迹，这就导致在观看整体矢量图时，会因为冗余痕迹的影响，导致整体的视觉效果降低。因此下一步需要研究的课题即：在该方法内添加滤波器，对冗余痕迹进行剔除。