基于改进ABC算法的模糊Elman变频空调温度控制

陈 以，莫 迪，陈睿星，孙俊佚雄

(桂林电子科技大学电子工程与自动化学院，广西 桂林 541004)

1 引言

由空调用电量大造成的夏季电网高负荷运行是电力网络中普遍存在的问题，目前华东地区夏季用电负荷高峰中有超过30%是由空调用电造成的，而在北京上海等城市甚至接近50%。如何有效的控制空调用电一直是空调研究领域的热点。文献[1]提出一种考虑时间约束的变频空调频率控制方法，通过对空调进行组网，在一定范围内限制空调运行功率来降低用电峰值。文献[2]同样基于需求响应提出了一种考虑热舒适度的多家庭变频空调群组恒温控制策略，在考虑用户舒适体验的同时实现负荷削减容量最大化。文献[1][2]的方法均是通过限制空调运行功率来降低用电峰值，虽然可行但仍在一定程度上影响了用户体验。从空调运行控制策略的角度研究，利用更加精确的智能控制方法限制空调温度超调，实现空调的节能运行，无疑会对用户更加友好。文献[3]，文献[4]，文献[5]等将模糊控制与神经网络相结合，建立模糊神经网络控制器对变频空调压缩机进行精确控制。文献[6]将神经网络与PID控制策略相结合，通过改善风机功率实现节能目的。受上述启发，本文将模糊控制规则引入Elman网络，建立模糊Elman网络控制器(FENC)对变频空调实现控制。针对网络训练中存在的易陷入局部极小点的问题，给出一种改进的人工蜂群算法(IABC)，在标准人工蜂群算法(ABC)的跟随蜂阶段引入模拟退火算法思想，通过设定模拟退火的作用范围保证权值优化算法的全局收敛。

2 变频空调模糊Elman网络控制器设计

模糊控制方法是当前应用于空调控制中的一种较为成熟的控制方法，具有推理性强，结构简单等诸多优点，但因受到控制规则条数的限制，其控制精度和动态品质均不够理想。要提高空调的控制精度，就要求控制系统对室内温度的特征信息有更强的处理能力。而Elman网络的连接层节点具有短时记忆功能，更适用于对变频空调这种大惯性和纯延时系统的控制。本文将模糊控制与Elman网络相结合，充分利用当前发展完善的温度控制规则，同时增强控制系统对温度时序数据的处理能力，力求提高控制精度，减小甚至消除温度超调。

考虑网络的输入量可以充分表征温度信息，同时网络的复杂度不宜过高，设计FENC为双输入单输出结构，以温度的偏差值e和偏差变化率ec作为输入，输出逆变电源的工作频率用于调节制冷压缩机的转速，从而实现空调对室内温度的控制。模糊化过程将输入量化为7个等级(NB，NM，NS，ZO，PS，PM，PB)，使FENC实现对49条规则的推理。网络结构如图1所示。

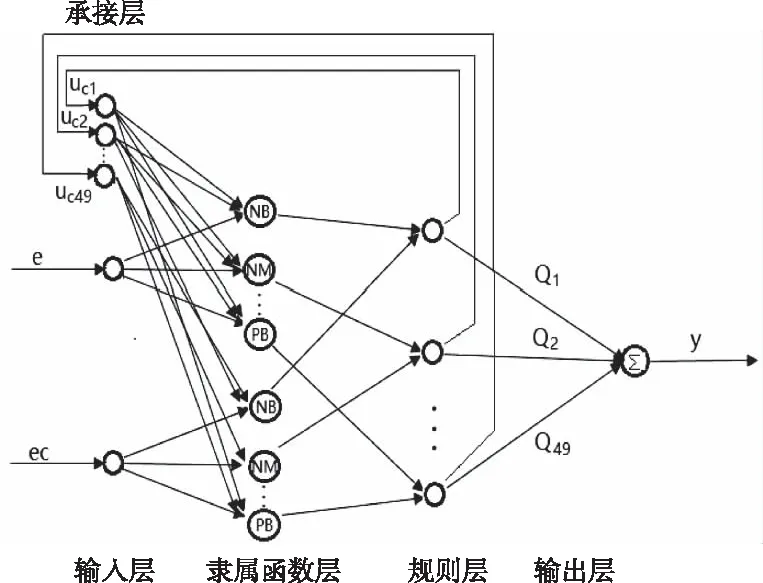
图1 FENC网络结构

输入层：该层包含温度和温度变化率两个输入向量

(1)

隶属函数层：每个节点对应一个语言变量，共14个节点，节点的输入由输入层输出和反馈变量组成，隶属度函数选用高斯函数。

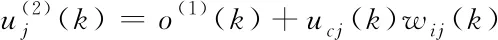
(2)

(3)

wij(k) 表示反馈环节第i个节点到隶属函数层第j个节点的连接权值，i=1，2，…，49，j=1，2，…，14，当j≤7 时o(1)(k)=e，当j>7时o(1)(k)=ec，cj与σj分别代表该层第j个节点的隶属度函数的中心值与宽度。

规则层：该层实现模糊推理的“与”运算，对规则进行提前推理，每个节点相当于一条规则且与上一层连接权值为1。模糊规则的形式如下

ifx1isA1jandx2isA2jand…andxnisAnj，thenyj(k)

=a0j+a1jU1+a2jU2+…+anjUn

其中Aij(i=1，2;j=1，2，…，7)为xi的第j个语言变量x(k)=[x1，x2]为规则的前件向量，U(k)=[U1，U2，…，U7] 为规则的后件向量。

该层的输入输出之间的关系为

(4)

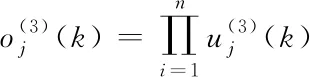
(5)

承接层：该层节点数等于规则层节点数，其作用为将当前时刻的规则层节点的输出值保存，反馈到隶属函数层节点用于下一时刻模糊推理。

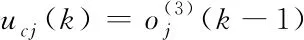
(6)

承接层使隶属函数层k时刻的输入信息包含了k-1 时刻的推理结果，从而使网络有了短时记忆能力，增强了网络对时间序列数据的处理能力[7]。

输出层：该层实现模糊规则的后件部分并完成网络的输出。

(7)

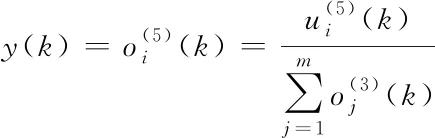
(8)

其中Qj(k) 为模糊后件推理的加权项

(9)

其中i=1，2，…，49;j=1，2，…，7

3 改进人工蜂群算法

对FENC网络的训练首先使用了经典的梯度下降方法，但因算法后期易陷入局部极小点，往往无法达到要求的训练精度。受当前变频空调主控CPU性能限制，FENC网络需离线完成训练过程，因而对训练速度的要求较低，选用收敛速度较慢但精度更好的人工蜂群算法(ABC)代替梯度下降法，在解空间生成多个可行解进行分布式并行随机搜索，以期解决复杂的FENC网络训练难以达到预定精度的问题。但ABC算法同样存在早熟收敛、易陷入局部最优[8]以及全局搜索能力和局部开发能力不平衡[9]的缺陷，为改善该问题提出改进的人工蜂群算法(IABC)。

3.1 人工蜂群算法的基本思想和改进方案

人工蜂群算法(Artificial Bee Colony， ABC)[10]中，蜂群由引领蜂、跟随蜂和侦察蜂组成。算法在初始化后进入引领蜂阶段，由引领蜂负责最初的蜜源寻找，在初始蜜源的基础上做一次随机的领域搜索，并根据新旧蜜源优劣比较判断是否更新蜜源，从而完成对蜜源的全局搜索。第二阶段为跟随蜂阶段，跟随蜂以某一蜜源的适应度值占所有蜜源适应度的比重为概率，决定是否对该蜜源周围进行随机搜索并更新，从而完成对蜜源的局部开发。当某一个蜜源在一定次搜索过后仍未进行更新，则该蜜源对应的引领蜂转化为侦察蜂，放弃该蜜源并重新搜索新蜜源。

标准ABC算法将全局搜索和局部开发相结合，具有模型简单，寻优精度较高，鲁棒性强等优点，但也存在局部搜索能力和全局搜索不平衡以及易陷入局部极小点的问题。因而在标准ABC算法的跟随蜂阶段引入模拟退火算法，提出一种改进的人工蜂群算法。

模拟退火算法的思想来源于冶金学材料退火过程，通过模拟金属热浴之后的退火过程，达到搜索优化问题全局最优解的目的[11][12]。该算法依据Metropolis准则，将温度与解的更新概率关联，即当ΔT<0时接受新解作为当前解，否则以概率e(-ΔT/T)接受新解代替当前解。[13]改进的人工蜂群算法通过以一定的概率接受适配度更低的恶化解，增强算法的局部开发能力，以改善算法后期陷入局部极小点的问题。

3.2 改进人工蜂群算法的数学描述

1)初始化阶段

该阶段对蜜源数目SN蜂群数量引领蜂个数/最大未更新次数limit /最大迭代次数或寻优精度/初始温度T和退火系数σ进行设置。同时根据式(10)对蜜源进行初始化

xij=xminj+rand[0，1](xmaxj-xminj)

(10)

其中：xij代表第i个蜜源xi的第j个维度值i∈{1，2，…，SN}，j∈{1，2，…，D}，xmaxj和xminj分别代表蜜源第j维的最大值和最小值。

2)雇佣蜂阶段

雇佣蜂在初始蜜源的基础上根据式(11)进行搜索，寻找新蜜源

νij=xij+φij(xij-xkj)

(11)

其中xk代表邻域蜜源，k∈{1，2，…，SN}且k≠i，φij∈[-1，1]。

通过式(12)计算新旧蜜源的适配度值并以贪婪算法判断是否要对蜜源进行更新，式中fi为待优化的目标函数

(12)

3)跟随蜂阶段 跟随蜂根据式(13)计算的概率对某一蜜源进行局部搜索，搜索的公式为(11)式。

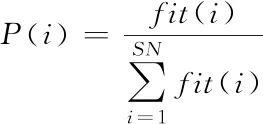
(13)

在该阶段的蜜源更新中引入模拟退火算法，当新蜜源的适配度低于旧蜜源时，以一定的概率p接受新的蜜源，其中

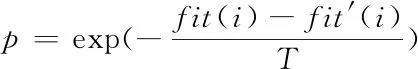
(14)

T为模拟退火算法的初始温度，且T(t+1)=σT(t)，σ∈(0.9，1)[14]，同时为了保证算法能够全局收敛，设定模拟退火算法起作用的范围为算法迭代的前m次，当N>m时，蜜源更新仅以贪婪算法为依据。标准ABC算法和改进后算法的蜜源更新公式分别为(15)式和(16)式

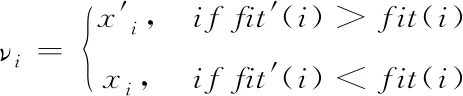
(15)

(16)

4 )侦察蜂阶段 当一个蜜源未被更新的次数超过限定值limit，则该蜜源对应的引领蜂变为侦察蜂，放弃该蜜源并根据(10)式重新探索新蜜源。

3.3 改进人工蜂群算法的有效性验证

改进算法在前m次迭代中引入了模拟退火算法的思想，使算法有更大的机率跳出局部极小点，获得更广泛的分布。该算法中，参数SN经初始化后变为一个确定的有限正整数，每个蜜源的维度以及各维度的搜索范围也是有限的，由此得到，整个蜂群状态序列的状态空间也是有限的。以结束第m 次迭代后的蜂群状态为初始状态，后续的人工蜂群状态序列由标准ABC算法得到，由文献[15]可得到结论，改进人工蜂群算法中蜂群的状态序列{Xn}为有限齐次马尔可夫链，进而可以证明该算法是全局收敛的。

本文通过选用表1中的两个单峰函数和两个多峰函数作为测试函数，检验ABC算法和IABC算法的收敛速度和收敛精度，验证IABC算法的有效性。

表1 标准测试函数

令D=2， 蜜源数目SN、引领蜂个数、跟随蜂数均为30，limit为50，最大迭代次数为1000，初始温度T0=1000，退火系数σ=0.95，进行多次测试，各测试函数的图像及测试结果对比如图2-图5所示。

图2 Sphere函数测试结果

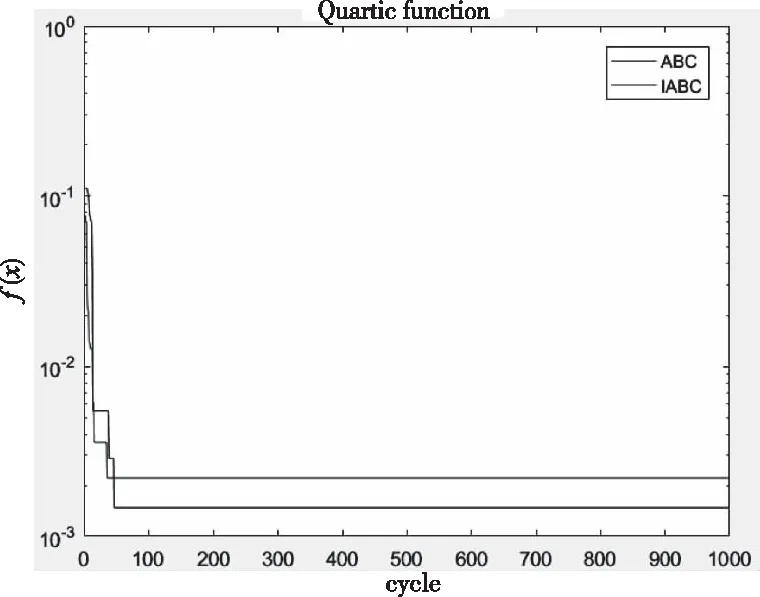
图3 Quartic函数测试结果

图4 Griwank 函数测试结果

图5 Rastrigrin 函数测试结果

验证结果表明，IABC算法与ABC算法相比，在模拟退火算法作用范围内的收敛速度会有所降低，但脱离局部极小点的能力得到了加强，算法的寻优精度也更高。

4 系统建模与仿真

4.1 室内空调温度控制系统数学模型的建立

为了使室内空气的传递函数具有易处理性和较好的稳定性，将室内变频空调温控系统简化为由一个一阶惯性环节和一个延时环节组成。在惯性环节中，由于空调器的室内金属热容量远小于空气的热容量，且空气的热阻大于金属的热阻，所以将空调器的金属部件构成的较小的惯性系数加入到室内空气构成的较大的惯性系数中，形成一个一阶惯性环节。其等效公式为：

(17)

其中T是一阶惯性环节的惯性系数。因为空气从空调中吹出后，需在房间内循环一周才能被空调中的室温探头检测到，所以存在延时环节。将e-τs代入式(17)得到如下公式：

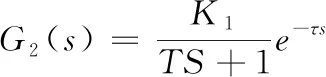
(18)

已知空气参数

ρ=1.225kg/m3，c=1.005kJ/kg·℃

带入公式T=m/Qm=ρvt/ρv′ 得到T=360，令系数K1为1.2，温度检测的延时时间为20s，将系数代入式(18)得到所需温度传递函数：

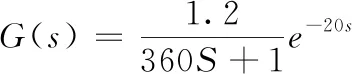
(19)

4.2 FENC网络的训练

为使FENC网络充分表达当前变频空调控制中成熟的模糊规则，从模糊规则曲面中均匀提取400个点作为网络的训练样本数据。模糊规则如表2所示。

表2 变频空调模糊控制规则

利用模糊工具箱建立模糊规则，使用evalfis函数从规则曲面中均匀提取400个点，进行min-max归一化处理之后作为FENC网络的训练样本。

前期的仿真在FENC网络的训练过程中首先使用梯度下降算法，图6为实验中出现训练后期陷入局部极小点的典型情况图像，纵坐标为误差绝对值，横坐标为训练次数。

图6 误差周期性震荡图像

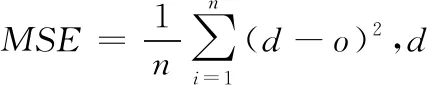
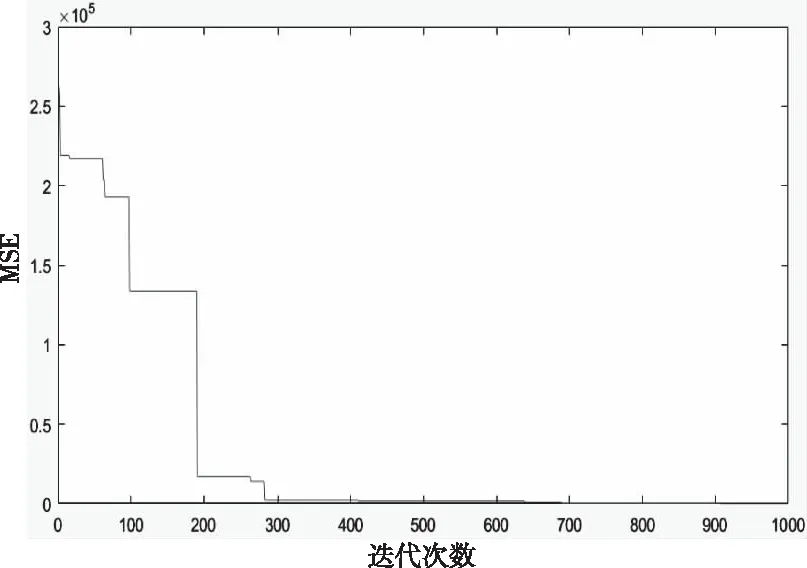
图7 IABC算法训练下的MSE变化

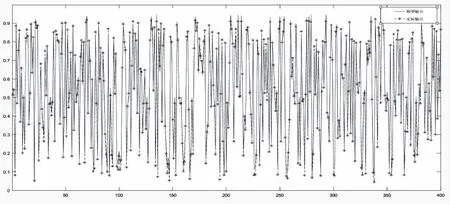
图8 IABC算法训练效果

4.3 系统仿真

将训练好的FENC网络控制器代入图9的变频空调温度控制系统，同时通过Matlab仿真实现PID控制方法和文献[5]中典型的模糊神经网络控制方法，与本文的模糊Elman网络控制方法做出对比，控制效果如图10所示。横坐标表示时间，单位为s，纵坐标表示温度变化量，单位为℃。

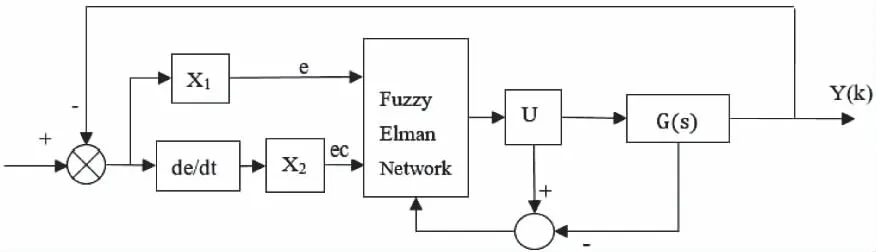
图9 变频空调温度控制系统框图

图10 控制系统仿真图

由图可见，传统的PID控制方法存在较大的超调和较长时间的震荡过度过程，由于该过程中变频空调压缩机产生制动力和调整加速力，其做功对改变环境温度无效，不仅造成用电浪费，同时也会影响变频压缩机、变频驱动模块的可靠性和使用寿命。文献[5]的模糊神经网络控制方法有效降低了变频空调的温度超调，同时缩短了系统响应的过度时间，使温度控制更加快速和精确。FENC方法经过完善的样本数据训练，相对文献[5]的方法，在控制系统超调方面有了更好的表现，实现对温度更加精确的的控制。综上所述，FENC方法相对于PID控制方法及模糊神经网络控制方法在控制温度超调方面有更好的效果，系统对温度的控制更加精确，使变频空调的运行可以更加节能。

5 结束语

本文将变频空调温度控制的模糊规则与Elman神经网络相结合，构造了用于变频空调室内温度控制的FENC网络控制系统。将模拟退火算法的思想与人工蜂群算法相结合，提出IABC算法，经测试，IABC算法相比ABC算法提高了局部搜索能力，改善了算法在训练后期易陷入局部极小点的缺陷，提高了训练精度。系统仿真表明，经过完善训练的FENC网络能够更有效的控制温度超调，实现更精确的控制，从而有效的减少变频空调能耗。