基于SAPSO的高速铁路受电弓型面优化

刘仕兵，张怡欣，李思明

(华东交通大学电气与自动化工程学院，江西 南昌 330013)

1 引言

随着高速电气化铁路的飞速发展，对运营质量提出了更高的要求。受电弓滑板磨耗现象广泛存在于高速电气化铁路中，并会造成较大的危害，一直是影响重载铁路运输安全性和稳定性的重要问题之一。受电弓受流过程是在动态中完成的，弓网受流质量是影响列车正常运行的关键，弓网受流技术是高速电气化铁路关键技术之一[1]。弓网磨耗的特殊性是受电弓滑板在接触网上滑行时会同时造成电气磨损、机械磨耗和化学磨耗，其中以机械磨耗为主。

国内外学者对直接的受电弓型面优化方面研究较少，但在不同方面对于受电弓磨损情况开展了一系列研究。陈忠华[2-3]等基于载流摩擦磨损试验机对弓网摩擦力建模，分析并研究波动载荷下弓网滑动电接触的载流特性及电弧干扰；杨红娟[4-6]等对弓网振动产生电弧等产生摩擦磨损分析了不同试验速度对受电弓滑板的磨损率、磨损形态以及摩擦系数的影响，并进一步研究了滑板振动与电弧产生的相关机理；戴利民等[7-9]基于滑板导线受流磨损试验样机对浸金属碳滑板材料进行了受流磨损试验，采用磨损量计量方法分析了不同的接触压力、电流、滑行速度对碳滑板材料的受流磨损性能的影响；王胜[10]结合Archard磨耗模型推导弓网摩擦副磨耗公式，对刚性平面悬挂布置提出了优化建议；Giuseppe等[11-12]基于弓网摩擦磨损试验平台，建立接触线与滑板的预测方程和预测数学模型，研究了弓网磨耗与材料、电流、表面的不平整性有关；Yang[13-14]分析了弓网摩擦副摩擦磨损性能与电弧、滑板振动有关，从滑板磨耗微观型面的角度研究了不同速度下的磨耗变化速率和磨耗累积量；任志强[15]通过对钢轨进行非对称型面优化，建立了钢轨磨耗速率优化模型。

本文以优化受电弓滑板型面降低受电弓磨耗量为目的，基于Archard磨耗模型建立受电弓滑板型面数学模型，通过模拟退火的粒子群算法得到最小磨耗体积，根据最小磨耗体积更新优化型面，降低优化后型面磨耗量，达到受电弓滑板型面优化的目的。

2 Archard磨耗模型

弓网系统中受电弓滑板与接触线相对滑动构成一对摩擦副，对于受电弓碳滑板来说，一般采用浸铜的碳滑板，分子机构较松散，容易在压力作用下产生脱离原组织结构的颗粒，造成机械粘着磨损，受电弓滑板颗粒在与接触线滑动接触下发生断裂，形成磨屑。弓网磨损过程中情况比较复杂，会同时发生电气磨损、机械磨损和化学磨损，电气磨损产生电弧，化学磨损形成氧化物改变动态接触摩擦力，两种磨损均加剧导致机械磨损，因此在弓网磨损情况中，机械磨损为主要磨损形式。由于弓网磨损情况复杂，本文选择机械磨损做为研究重点。

英国Leicester大学工程系教授J.F.Archard在R.Holm和Burwell、Strang工作的基础上，于1953年提出粘着磨损理论[16]。

在对受电弓碳滑板磨耗累积深度的计算中，本文采用摩擦和摩擦磨损理论中广泛运用的Archard磨耗模型

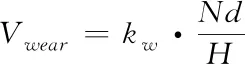
(1)

其中，Vwear所求的磨耗体积，kw为无量纲的磨耗系数，N为受电弓滑板与接触线的法向力，d为受电弓滑板相对滑动距离，H为相对软的材料的硬度。

Archard理论模型如图1所示。

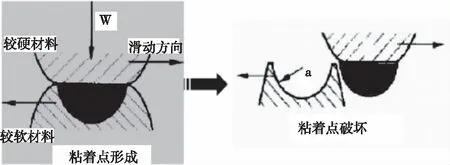
图1 Archard理论模型

由模型可知，假设在单位面积上有n个粘着颗粒滑动发生破坏，每个破坏的颗粒视为半径为a的圆体，其压缩屈服极限为σs，则接触线与受电弓碳滑板之间的压强W为

W=n·π·a2·σs

(2)

当受电弓碳滑板与接触线相对滑动，粘着点分离时一部分粘着点从碳滑板中被拉出。即磨损体积公式为

ΔV=(2/3)·π·a3

(3)

引入磨损常数k代表部分断裂粘着点，当位移为2a时，此时单位位移下产生的体积磨损量公式演化为

ΔV/Δl=(1/3)·k·π·a2·n=k·W/(3·σs)

(4)

摩擦副磨耗示意图如图2所示。

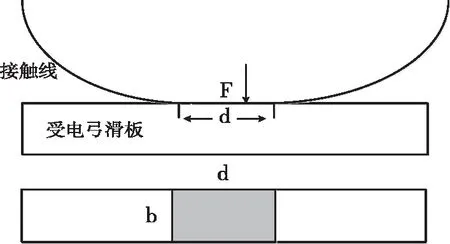
图2 摩擦副磨耗示意图

假设受电弓与接触线间的动态接触力为F，接触面积表示为db区域的阴影部分，因此在弓网接触面处受电弓受到压强W为：

W=F/(b·d)

(5)

假设压缩屈服强度σs与受电弓碳滑板硬度H相等，代入(4)式，则单位长度碳滑板磨损公式为：

V=(k·F)/(3·H·b·d)

(6)

其中V代表受电弓碳滑板单位长度上的体积磨损，则由此式可得：受电弓碳滑板磨损体积与磨损深度成正比，体积磨损量可以代表碳滑板的磨损程度或者磨损率。符合本文下述数学模型选用磨损体积作为优化目标。

3 基于SAPSO的受电弓型面优化模型

3.1 受电弓型面数学优化模型

受电弓滑板与接触线在接触的过程中受到电气、机械、化学、材料等因素的影响，使得覆盖在接触线与受电弓表面上导电率较差的表面膜从接触线和碳滑板表面移走，从而导致接触线与受电弓滑板的磨耗。当接触线与受电弓滑板之间的接触压力提高时，机械磨损为主要磨损形式；接触压力过小时，电气磨损加剧。结合实际工况，发现受电弓碳滑板磨损规律，受电弓碳滑板的磨耗主要集中在距受电弓中心线±200mm范围内，不均匀磨耗明显，分布不合理。

实际的表面接触结构如图3所示：

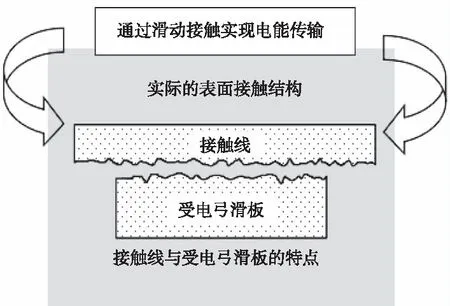
图3 实际表面接触结构

在实际的受电弓滑板与接触线表面接触中，存在严重的的表面不平顺。而这种现象极易加重受电弓滑板与接触线的磨损情况。因此受电弓型面优化则考虑将其优化为平顺的接触结构。

受电弓型面理想磨耗示意图如图4所示。

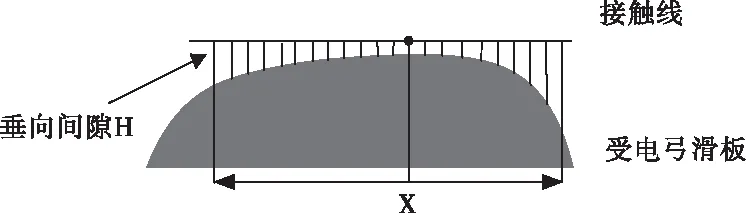
图4 受电弓型面理想磨耗示意图

图4为受电弓与接触线横截面理想状态，垂向间隙为原始受电弓磨损深度，其中受电弓滑板与接触线接触磨耗的垂向间隙所围成的区域围磨损面积与宽度d相乘则为受电弓磨耗体积，垂向间隙与工作区域X围成的面积区域作为需要优化区域。将受电弓滑板工作区域X离散为t个点，得到垂向间隙H的公式为

(7)

为建立受电弓碳滑板磨耗优化型面数学模型，需将受电弓型面进行离散化处理，将实际模型转化成所需要的数学模型。如图5所示，工作区域X用一系列独立自变量函数x1，x2，…xn来表示，目标函数为f(x1，x2，…xn)表示为体积磨损量，对自变量x1，x2，…xn施加一定的约束条件。优化受电弓磨耗型面的目标是获取目标函数的最小值f(x*)，寻找一组最优解x*，然后根据最优解x*拟合得到优化后的受电弓磨耗型面。

图5 受电弓型面离散化

选择受电弓滑板在实际运营条件下与接触线接触到的区域±220mm作为优化区域。将工作区域的两端设定为固定点，将工作区域离散为t个间隔足够小的点，可动点可以沿着y坐标方向移动，通过可动点的上下移动来改变受电弓碳滑板磨耗型面的状态。取每个可动点的y坐标相对于原始坐标的改变量Δy1，Δy2， …Δyn作为独立自变量。由每组Δy1，Δy2， …Δyn最优解的值，通过样条曲线函数绘制出新的受电弓碳滑板磨耗型面。达到受电弓磨耗型面的优化目的。

本文以体积磨损量作为优化的目标函数，取垂向间隙H为所求解，取t个间隔足够小的横移量为ΔX，图4中阴影横截面积与受电弓碳滑板宽的乘积即为体积磨损量。受电弓碳滑板宽度为恒定值350mm，因此磨损率可由H-ΔX与横轴所围成的区域面积公式表示

(8)

其中，ΔX表示受电弓滑板的横移量ΔX的迭代步长，t表示离散值数目，Hi表示对应的垂向间隙。

受电弓碳滑板与接触线之间的接触形式为线接触，两者接触在一条直线上，实际上接触面是分布在狭长区域内的若干个接触点。如图2所示，受电弓与接触线接触范围宽度为受电弓宽度即为固定值，则单位长度的受电弓碳滑板磨耗型面累积的磨耗量V在一定程度上可与H-ΔX与横轴所围成的区域面积S关系相对应，体积磨损量V在某种意义上可由区域面积S表示，即为所求目标函数值。

为了满足实际问题的要求，获取合理的优化结果，需要对Δy1，Δy2， …Δyn自变量进行约束。为保证优化过程中型面曲线不出现波浪形，优化后的受电弓滑板型面需满足凸曲线的条件，相邻点间线段的斜率应满足随着横坐标的增大而减小

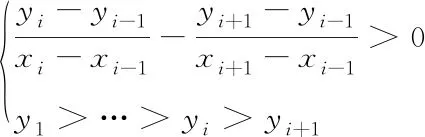
(9)

对受电弓滑板与接触线的型面优化必须是建立在原标准型面的基础上，同时受电弓滑板需要满足打磨最大磨耗深度的要求

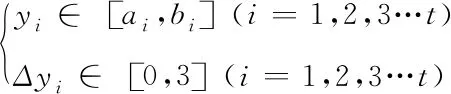
(10)

优化型面的动力学指标函数D(yi)需满足为受电弓正常运行情况下的相应指标的限值d。通过对优化模型约束分析，满足以上所有约束条件下最终建立受电弓碳滑板体积磨损型面优化的数学模型为

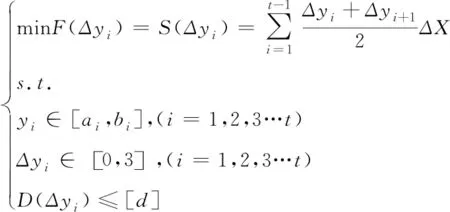
(11)

3.2 模拟退火的粒子群算法

粒子群算法的原理是初始化一群无规律粒子在可行解空间S中，每个粒子寻找个体最优解并向全局最优解靠近。相对于其它智能优化算法来说，粒子群算法设计简单，计算方便，求解速度快；但容易陷入局部最优的问题[17]。为改善此问题，本文在原基础上通过模拟退火的方式改进。在标准粒子群算法中，ω的取值一般具有经验性，不具有通用性。因此在本文中将它设为0，则进化方程表示为

(12)

初始化所有粒子，随机设置粒子的初始速度与初始位置，当惯性权重设置为0时，粒子的速度不具有记忆性，将全部粒子向全局最优值靠近，使得全局搜索能力减弱。当达到xj(t)=pi=pg条件时，第j个粒子停止进化。此时，保留pg当前位置作为粒子的全局历史最优，然后重新在搜索空间S中随机产生粒子j的新位置xj(t+1)，对应的xi(t+1)通过式(12)产生。粒子产生过程如下式所示

pj=xj(t+1)

(13)

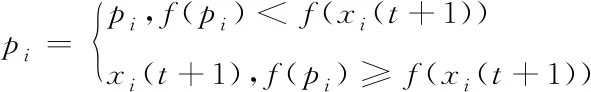
(14)

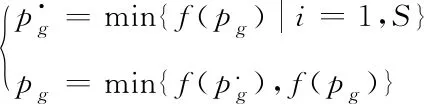
(15)

在上述粒子进化过程中，至少需要有一个粒子在S空间中重新产生，以避免粒子陷入局部最优解。搜索空间S随机产生的粒子j定义出现在给定解邻域中，通过模拟退火算法随机产生，接受准则允许目标函数在有限范围内变坏，以一定概率接受新的可行解，以避免粒子陷入局部最优解影响算法结果。

以当前历史最好位置pg为初始状态，选择初始温度T=T0，通过式(16)产生下一状态的各个粒子

xj(t+1)=xj(t)+ηε

(16)

其中η为扰动幅值参数，ε为随机变量一般服从均匀分布或正态分布。

两个粒子的位置引起的适应值变化量由式(17)所得

ΔE=f(xj(t))-f(xj(t+1))

(17)

当ΔE≦0时，接受新值，否则拒绝接受。当接受新值时，按照下式开始降温

T(t+1)=αT(t)，0<α<1

(18)

4 运行结果分析

在受电弓与接触线滑动接触中，受电弓碳滑板与接触线之间的接触形式为线接触，实际上接触面是由分布在狭长区域内的若干个接触点组成。通过设置每一迭代步的累积磨耗深度上限值，则受电弓滑板在当前迭代步内行驶的距离通过受电弓滑板运行的速度和时间可以计算得到，并将结果作为当前迭代步步长ΔX带入目标函数计算。

本文选择采用模拟退火的粒子群算法来优化受电弓滑板磨耗型面工作区域与接触线接触到的区域±220mm，根据模拟退火的粒子群算法参数设置本文中相关参数分别为：取学习因子c1为2.0，c2为2.0，粒子初始飞行速度为0.5，粒子最大飞翔速度为0.6，粒子种群规模为30，迭代次数为300，退火常数为0.5。通过Matlab软件编制程序，得到运行结果如图6、图7所示。

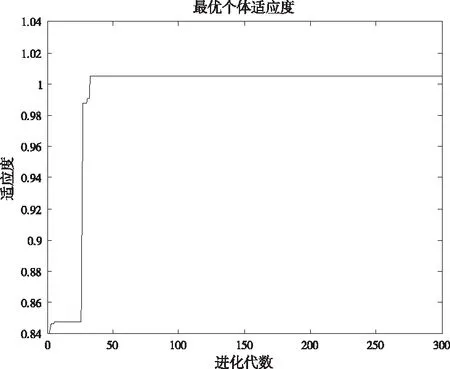
图6 最优个体适应度

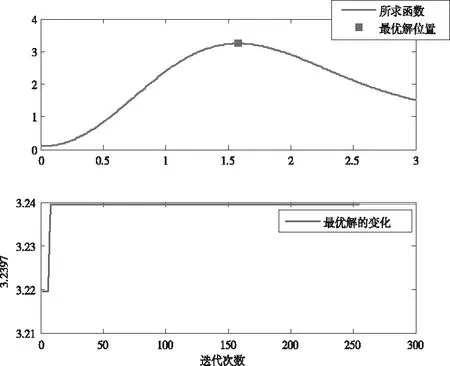
图7 全局最优解

根据受电弓滑板的最小体积磨耗量对应的一组最优解的对受电弓滑板与接触线的接触型面进行更新，更新后的磨耗型面作为初始的磨耗型面代入下一迭代步进行计算。优化后型面相对原始型面拥有更好的共形度。当受电弓滑板沿着接触线相对滑动时，受电弓滑板与接触线的接触点位置能够更加持续发生变化，接触线的振动幅度降低，减少了受电弓磨损量，延长了受电弓碳滑板的使用寿命，达到了优化的目的。

如图8所示，算法达到收敛，能够表明在优化后的受电弓滑板的磨耗型面的体积磨损量持续增加，但优化后的受电弓磨耗型面斜率变化更加平滑，保证了受电弓滑板与接触线良好接触，能够有效降低弓网的离线率，减少电弧现象，有利于改善弓网间的接触性能，受电弓滑板与接触线的磨损体积也将相对原始型面进一步缩小，达到了优化目的。通过优化后，受电弓滑板的磨耗型面的弓头运行轨迹更为平缓，振动频率降低减缓，接触网的弹性不均匀度没有增加，有效改善了受电弓与接触线滑动接触的机械磨耗与电气磨耗。算法可行性得到了验证。

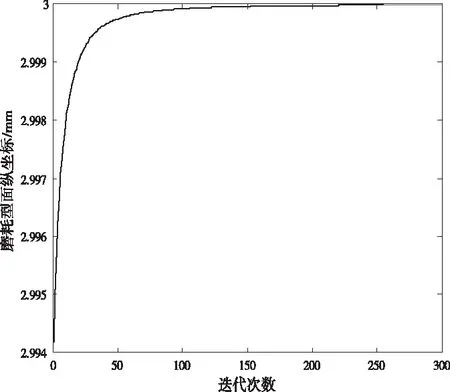
图8 算法收敛曲线

5 结论

1)将Archard磨损模型结合到受电弓碳滑板与接触线磨耗模型中来，通过换算验证得到体积磨损量可以表示碳滑板的磨损程度与磨损率。为受电弓碳滑板磨耗模型的建立提供了一定的理论依据。

2)建立受电弓型面优化的数学模型，将受电弓磨耗型面离散化，设定目标函数与约束条件，目标函数为最小体积磨损量，得到体积磨损量对应的一组最优解，再通过样条函数将最优解拟合成新的型面，完成受电弓的型面优化的目的。

3)通过模拟退火的粒子群算法使用Matlab编制程序并进行仿真计算。得到优化后型面共形度优于原始型面，有效改善受电弓与接触线接触性能，降低了受电弓碳滑板磨损程度。