基于方差分析的航班离地地速影响因素研究
陈文瑛副教授 傅佳萍 齐 凯,3
(1.首都经济贸易大学 管理工程学院,北京 100070;2.城市群系统演化与发展的决策模拟研究北京市重点实验室,北京 100071;3.山东航空股份有限公司,山东 济南 250000)
0 引言
民航飞行安全关系到旅客生命和财产的安危,因此对飞行安全影响因素进行研究是非常有必要的。起飞阶段是飞行过程的关键阶段之一,飞机在该阶段容易发生冲出/偏出跑道事故,对飞机和机上人员的生命构成重大威胁。据统计,在一次飞行中,起飞阶段、最后进近和着陆阶段时间约只占总飞行时间的6%,但有近50%的事故,33%的致命事故和22%的死亡人数发生在此阶段,而飞机冲偏出跑道是起降阶段事故发生率较高的事故之一。由此国内外学者对飞机冲偏出跑道的原因进行分析研究,如:国内学者孔祥骏、杨开等分别利用历史数据从“人—机—环”角度,发现导致冲偏出跑道事故主要原因是飞行员操作不当、气象条件复杂、机组管理等,为研究冲偏出跑道事故风险因子间的关联性奠定基础;张晓全等在国内首次应用寻因分析法对冲偏出跑道事故进行危险源辨识,发现事故危险源包括天气原因、机组资源等方面问题;赵宁宁等利用事故树和贝叶斯网络模型对飞机偏冲出跑道事故的风险进行分析,发现“飞行员操作有误”发生概率较高,其次分别为“飞行员判断有误”“飞机故障”“飞机相关系统突然失效”“跑道摩擦系数较小”和“跑道道面湿滑”;王浩宁等基于系统理论的事故模型,发现在飞机冲偏出跑道事故中机组人员可能存在不安全控制行为。国外学者Marisa Jenkins研究指出风、道面情况和起降距离是飞机冲偏出跑道事故的主要原因;Distefano等创新性地采用多重对应分析法对冲偏出跑道事故进行分析,发现起飞阶段发生该类事故最常见的原因是飞机系统故障;Pramono等分析事故报告,第一次调查印尼航空事故的因素,指出天气、机组资源管理、跑道条件技术故障等是导致冲偏出跑道的原因。大多文献通过历史事故数据或飞机构造分析探究发生冲偏出跑道事故原因,研究发现机组资源管理对飞机冲偏出跑道有影响。轮胎爆胎是机组资源管理失效的一种情况,而导致轮胎爆胎原因很多,其中起飞时离地地速过大是导致轮胎爆胎的重要诱因之一。
目前,较少有研究基于飞行数据分析该类事故的风险因素,本文根据专家意见及快速存取记录器所采集的机型为B738的民航飞机飞行数据信息,应用方差分析方法,从机重、温度和人的操作3个角度入手,识别飞机起飞离地地速的影响因素,研究这些因素对飞机离地地速的影响程度,可为降低飞机冲偏出跑道事故风险提供科学依据。
1 研究方法
方差分析用于分析研究不同来源的变化因子对总体变化的贡献能力,进而确定变化因子对研究结果的影响大小。本文应用这种方法考察不同风险因子对飞机离地地速是否有影响及影响的程度。
方差分析是用于检验不同水平下某因变量的均值变化是否显著的一种定量分析方法,包括单因素方差分析、多因素方差分析等,利用此方法可以分析出某一因素是否为因变量的影响因素。因数据的限制,本文仅通过单因素方差分析来识别导致飞机离地地速v
过大的风险因子。单因素方差分析,也称一维方差分析,是用来研究一个控制变量的不同水平是否对观测变量产生显著影响的方法,换句话说,就是检验3个或3个以上独立样本观察值的各组平均数是否相等。其对数据的要求为:观测变量为数值型变量,控制变量为分类型变量,分类型变量的每一种具体表现形式称为控制变量的水平。除此之外,在使用方差分析前,各组观测值必须满足正态性、独立性及方差齐性3个条件。对于单因素方差分析结果,可通过关联强度指数ω
衡量自变量的不同因子水平对因变量的贡献程度,关联强度计算公式:
(1)
式中:
ω
—关联强度指标;k
—自变量因子水平;MSE—组内均方值;
SSA—组间平方和;
SSE—组内平方和;
SST—总离差平方和,SST=SSA+SSE。
关联强度指数ω
高低判断自变量与因变量关联程度的标准:关联强度指数ω
在6%以下,属于微弱关系;关联强度指数ω
位于6%~16%之间,属于中度关系;关联强度指数ω
大于16%,属于强度关系。本文采用SPSS软件对数据进行统计分析,从而得到方差分析结果,以分析机重、温度和人的操作对飞机离地地速的影响。
2 数据来源及预处理
轮胎爆炸可能导致冲偏出跑道事故,而飞机离地地速v
过大是飞机爆胎的重要诱因之一,本文主要探究导致轮胎爆胎因素间的关系,即温度T
、机重G
和人为操作对飞机离地地速ν
的影响,如图1。在8位航空安全管理和飞行品质管理方面专家的指导下,选定起飞过程的抬轮时间差t
、离地时仰角θ
、发动机低压转子最大转速百分比N
、最大仰角增加率α
、平均仰角增加率β
作为表征人为操作的参数。由此,提取2019年7月246架次飞机离地瞬间的246条数据。数据包括v
、G
、T
、t
、θ
、N
、α
、β
等,由于篇幅有限,仅列出部分数据, 见表1。由于采集的是单机场的数据,所以未考虑标准气压对ν
的影响。t
是实际抬轮时刻与理论抬轮时刻的差值。
图1 可能导致飞机爆胎进而冲偏出跑道因素间的逻辑影响关系
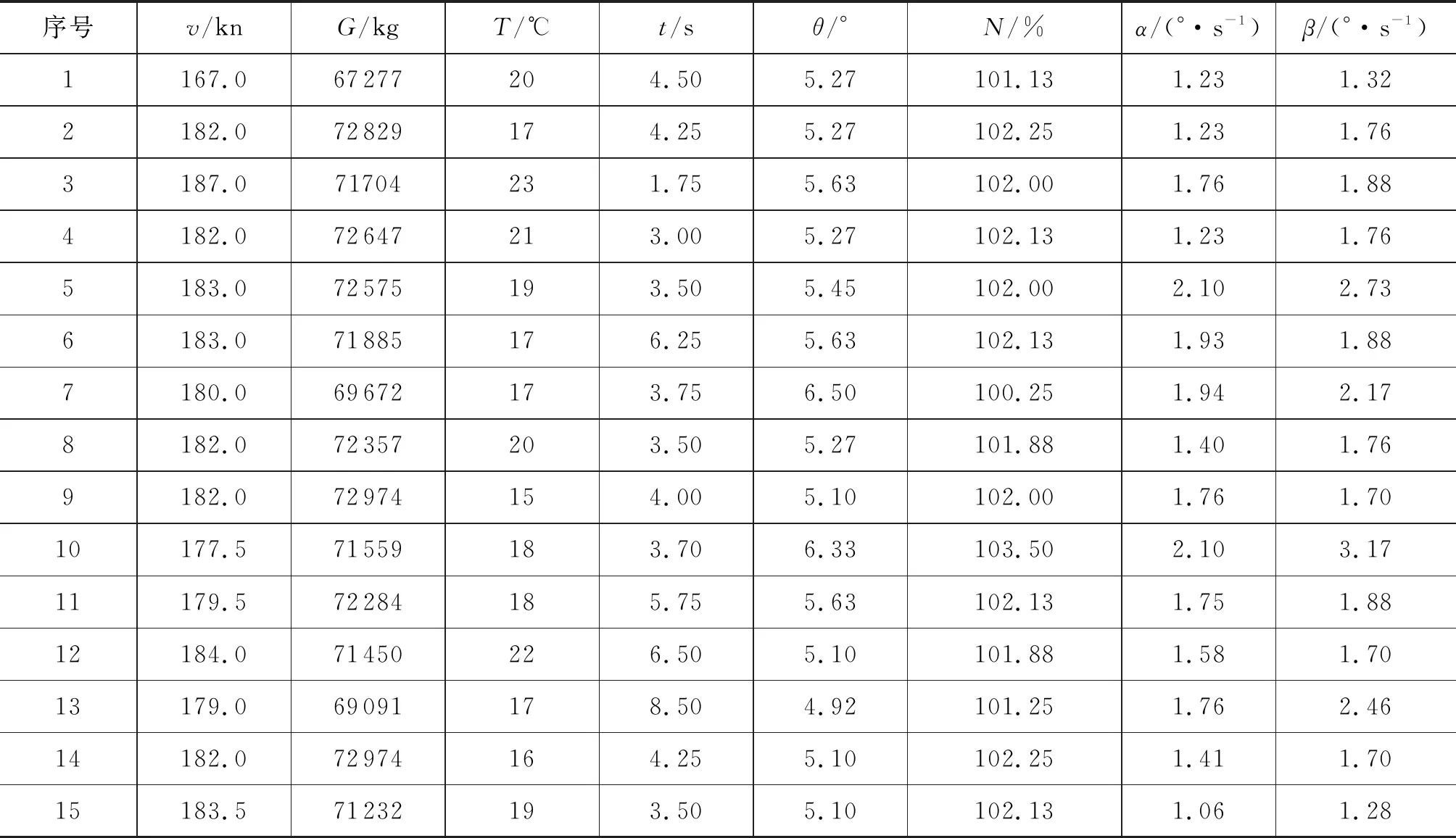
表1 某航空公司2019年7月部分飞行纪录
本文将ν
作为因变量,G
、T
、t
、θ
、N
、α
、β
作为自变量,观察数据发现,因变量和自变量都为数值变量。为把T
等自变量数据转化为分类变量,需要对自变量数据进行分组。数据分组的方法有单变量值分组和组距分组2种。单变量值分组是把每一个变量值作为一组,这种分组通常只适合离散变量,且在变量值较少的情况下使用。在连续变量或变量值较多的情况下,通常采用组距分组,即将全部变量依次划分为若干个区间,并将一个区间的变量值作为一组。根据数据特征,这里对T
进行单变量值分组,对G
、t
等进行组距分组。同一温度下的观察值划为一组,共有11个不同的温度,即11个组;对于G
、t
等自变量数据,这里通过斯特杰斯经验公式,对数据进行分组,经验公式:
(2)
式中:
C
—组距;n
—总次数;Max—最大值;
Min—最小值。
通过式(2)确定分组所需组距和组数,再对数据进行分组。由于对数据单因素方差分析时,需要每组数据有3个或3个以上的观察值,所以得到的分组结果若不满足该条件,则应去掉该组数据后重新分组。例如,对G
的数据进行分组:首先,将最大值72 974、最小值62 378以及总观测次数246代入式(2)中进行计算,得到组距为1 187.23,组数10组,之后发现位于第一组的数据只有一条,分组结果不满足单因素方差分析的条件,原因是该条数据与其他数据间的差值较大。通过对数据进行删减后重新分组,将G
的变量值共分为9组且每组都包含3条及3条以上的数据;其他数据的分组过程类似,具体分组结果,见表2。
表2 自变量数据分组情况
3 结果分析
3.1 正态性及方差齐性检验
方差分析需要对因变量的观察值进行正态及方差齐性检验。首先,本文采用分位数—分位数图(Quantile-quantile Plot,Q-Q)来判断是否满足正态分布。Q-Q图的纵坐标为预期的正态值,横坐标为样本点的实际取值。如果样本集合的概率分布与正态分布十分相似,那么Q-Q图逼近一条直线。对因变量观察值(即ν
的变量值)进行正态检验,如图2。由图2可见,ν
数据拟合后近似为一条直线,说明数据近似服从正态分布。
图2 ν的正态Q-Q图
然后,分别对在G
、T
、t
、θ
、N
、α
、β
下的v
的观察值进行方差齐性检验,从而判断数据是否满足方差齐性,见表3。
表3 自变量观察值的方差齐性检验结果
由表3可知,在方差齐性分析时,计算所得P
值都大于0.05,说明满足方差齐性条件,即可进行单因素方差分析。3.2 结果分析
分别对G
、T
、t
、θ
、N
、α
、β
等因素对ν
的影响进行单因素方差分析,见表4。由表4结果可得,G
、t
、N
所得P
值都小于0.01,说明这些因素对v
的影响极其显著;θ
的P
值小于0.05,说明θ
对v
的影响显著;而T
、α
、β
的P
值大于0.05,说明这3个因素对v
的影响不显著。在反映人为操作的5个因素中,有3个因素对v
的影响显著,说明人为操作对飞机离地地速的影响显著。进一步分析结果可以发现,v
的总变异量由G
、t
、θ
、N
解释的百分比分别为22.44%、6.05%、3.88%、10.11%(ω
=0.224 4、0.060 5、0.038 8、0.101 1)。其中,θ
与v
的关联强度指数为3.88%,小于6%,说明其与v
的关联强度属于微弱关系;t
、N
与v
的关联强度指数分别为6.05%、10.11%,位于6%~16%之间,说明这2个因素与v
的关联强度属于中度关系;G
与v
的关联强度指数为22.44%,大于16%,说明G
与v
的关联强度属于强度关系。
表4 不同自变量下因变量的单因素方差分析结果
为进一步了解v
的观察值均值间的差异,分别绘制不同G
、t
、θ
、N
水平下观察值的均值图,如图3。图3可知,飞机越重,v
越大;当抬轮时间差较大时,v
偏大,说明相较理论抬轮时间,若实际抬轮时间越晚,更可能导致v
过大;当θ
偏小时,v
偏大;N
偏大时,v
偏大。
图3 飞机重量与人为操作因素的飞机离地地速v均值图
可见,经过单因素方差分析,最终发现飞机重量G
、人为操作(如带杆和加油门)对民航飞机离地地速有显著性影响。其中,在表征人为操作的因素中,t
在起飞过程中,抬轮时间晚于理论值时,会导致v
偏大;若离地时仰角偏小时,容易导致v
偏大;N
值偏大时,v
也偏大。上述结果说明飞机重量、人为操作是飞机轮胎爆胎的间接诱因,在赵安家等对轮胎构造以及常见故障分析中有所体现。4 结论
本文分别对G
、T
、t
、θ
、N
、α
、β
下的飞机离地地速观测值进行单因素方差分析。其中,t
、θ
、N
、α
、β
表征人为操作,通过分析这些因素与v
的关系,反映人为操作对v
的影响,最终得到如下结论:(1)运用单因素方差分析,在0.05显著性水平上,分析得到有显著性差异的影响因素为G
、t
、θ
、N
,即机重和人为操作(带杆、加油门)对v
影响显著。(2)对单因素方差分析结果表现为显著性的因素进一步分析发现:在不考虑其他条件(如发动机推力、控制系统响应等)下,飞机越重,v
越大;在表征人为操作的因素中,若在起飞过程中,抬轮时间晚于理论值时,会导致v
偏大,若离地时仰角偏小时,也容易导致v
偏大,而就N
而言,其值偏大时,v
偏大。飞机起飞过程实际上是一个动态、多因素影响的优化问题,由于数据限制,本文仅通过单因素方差分析简单地得到机重和人为操作(带杆、加油门)对离地地速有显著性影响,希望对民航航班机组的实际操纵具有指导意义。

