一种永磁同步电机位置传感器故障保护控制方法

段卓琳，蒋雨菲，董星言，王伟洋，杨金波

(北京航天发射技术研究所，北京 100076)

0 引 言

为实现永磁同步电机的矢量控制，位置反馈信号必不可少。传统的转子位置或速度信息的反馈通过编码器、霍尔器件、旋转变压器等物理位置传感器实现，具有反馈值准确、控制方法简单的优点。然而，在电机运行过程中，位置传感器有很大的损坏风险，降低了系统的可靠性，由此导致的后果在一些军事应用领域会非常严重。为此，进行永磁同步电机的位置传感器故障保护控制很有必要，传统方法采用永磁同步电机的无位置传感器控制技术，通过检测永磁同步电机的一些电信号，从中提取或在线估计出电机的转速和位置信息[1-4]。然而，永磁同步电机无位置传感器控制算法的控制精度低于传统基于位置传感器的控制，且存在转速适用范围，一种基于电机基频动态模型进行转子位置估计，适用于电机中、高速运行的情况；另一种利用电机的凸极性，进行高频信号注入等，适用于电机零速和低速，但计算量大，且会产生一定的转矩扰动[5-7]。

本文提出将常用于永磁同步电机自抗扰控制中的扩张状态观测器方法应用于位置传感器故障保护控制中。基于电机基频动态模型的扩张状态观测器(以下简称ESO)方法[8-9]，具有稳定性好、适应性高、对模型信息要求低等优点。该方法将永磁同步电机实际运行过程中随转子位置变化而变化的反电动势视为系统的一个扩张状态，从而估算电机转子角度。电机正常工作时，通常运行于中高速转速的额定转速，采用位置传感器控制，输出的角度参与控制；而在位置传感器出现故障时，能够及时辨识出位置传感器的故障状态，并采用ESO算法估算角度进行控制替补位置传感器的功能，实现故障保护控制，保证任务持续进行，从而在不增加硬件结构和成本的情况下增加产品的可靠性及容错性能。本文进行了理论推导、软件设计，最后搭建电机对拖实验台架，通过实验验证了本方法的有效性。

1 基于ESO的无位置传感器控制算法

1.1 ESO算法原理

ESO方法将能够影响被控输出的扰动状态扩张成新的状态变量，从而较好地跟踪不确定对象的扩张状态[8-9]。在现代控制理论中，对于如下的二阶系统：

(1)

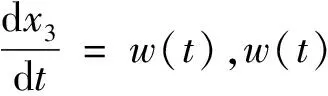
(2)

对式(2)建立其状态观测器方程可得：

(3)

式中：z1是x1的估计；z2是x2的估计；z3是系统总扰动x3的估计；β1，β2，β3是系统可调节的参数。

此时系统的误差方程可写：

(4)

式中：e1=z1-x1，e2=z2-x2，e3=z3-x3。只要f(x1,x2,t)有界，则总可以找到合适的参数β1，β2，β3及函数g(e)，使得式(4)稳定，且稳态误差值足够小[10]。

式(3)除了可以跟踪系统的状态变量x1，x2以外，还可将系统模型的未知部分f(x1,x2,t)视为一个新的状态变量，对其进行估计，因而式(3)称为ESO方程。由式(3)可知，建立ESO方程仅需要了解被测对象的相对阶数及参数b，对模型的信息要求低。

1.2 基于ESO的永磁同步电机转子位置估算方法

永磁同步电机在两相静止坐标系下的电压方程如下：

(5)

式中：Rs为电机定子电阻；Ls为电机电感，对于凸极永磁同步电机，Ls=(Ld+Lq)/2；eα、eβ为在αβ坐标系下的电机反电动势。

由式(5)可看出，永磁同步电机在α坐标轴下与在β坐标轴下的模型一致。以α坐标轴为例，永磁同步电机的电压方程可视为一阶线性系统，则其状态方程可写为：

(6)

式中：x1=iα，x2=eα。

对式(6)，以iα、eα为被观测对象，令其估计值分别为z1α、z2α，建立系统的状态观测器方程：

(7)

式(7)可展开表示：

(8)

同理，以iβ、eβ为被观测对象，也可类似建立永磁同步电机在β坐标轴下的扩张状态观测器方程。由式(8)即可得到反电动势eα、eβ的估计值z2α、z2β。

电机反电动势eα、eβ的表达式：

(9)

由式(8)观测得到eα、eβ的估计值z2α、z2β后，根据下式即可计算得到电机转子位置角θ：

(10)

根据式(5)、式(8)，可得到反电动势eα至其ESO估计值z2α的传递函数：

(11)

式中：β1，β2为控制参数，通过带宽的概念确定。按照文献[11]中的标定方法，将式(11)调整为标准形式：

(12)

令k=1/Ls，则式(11)可写：

(13)

式中：

播种花生时，一定要选晴天，这样做的目的，是为了让花生可以提前开花，有效避免干旱期，帮助提升花生产量，在条件允许的前提下，遵照“尽早播种”的基本原则，这样可以增加有效积温，促进花生提早开花，也可以帮助提升花生产量。假设在某一时间段内下雨量大且集中，就会严重冲刷土壤，非常不利于花生的生长和总产量的提升。

(14)

式中：ωc为截止频率，ωc=2πfc。

同理，反电动势eβ至其ESO估计值zβ的传递函数也可表示为类似的形式。

对于电机控制系统，通常选取截止频率为额定电频率的3倍，在根据电机转速选定ωc后，即可由式(14)计算得到系统状态观测器方程中控制参数β1，β2值。

以上ESO观测转子角度时的能够收敛，根据Lyapunov稳定性函数，在文献[12]中已经得到了证明。

2 控制算法软件设计

在基于ESO算法计算得到永磁同步电机控制系统的估计转子位置角度、转速后，即可通过角度值、转速值进行估计转子位置与实测转子位置之间的选择和切换，从而获得系统的位置传感器故障保护控制算法，控制算法控制框图如图 1所示。

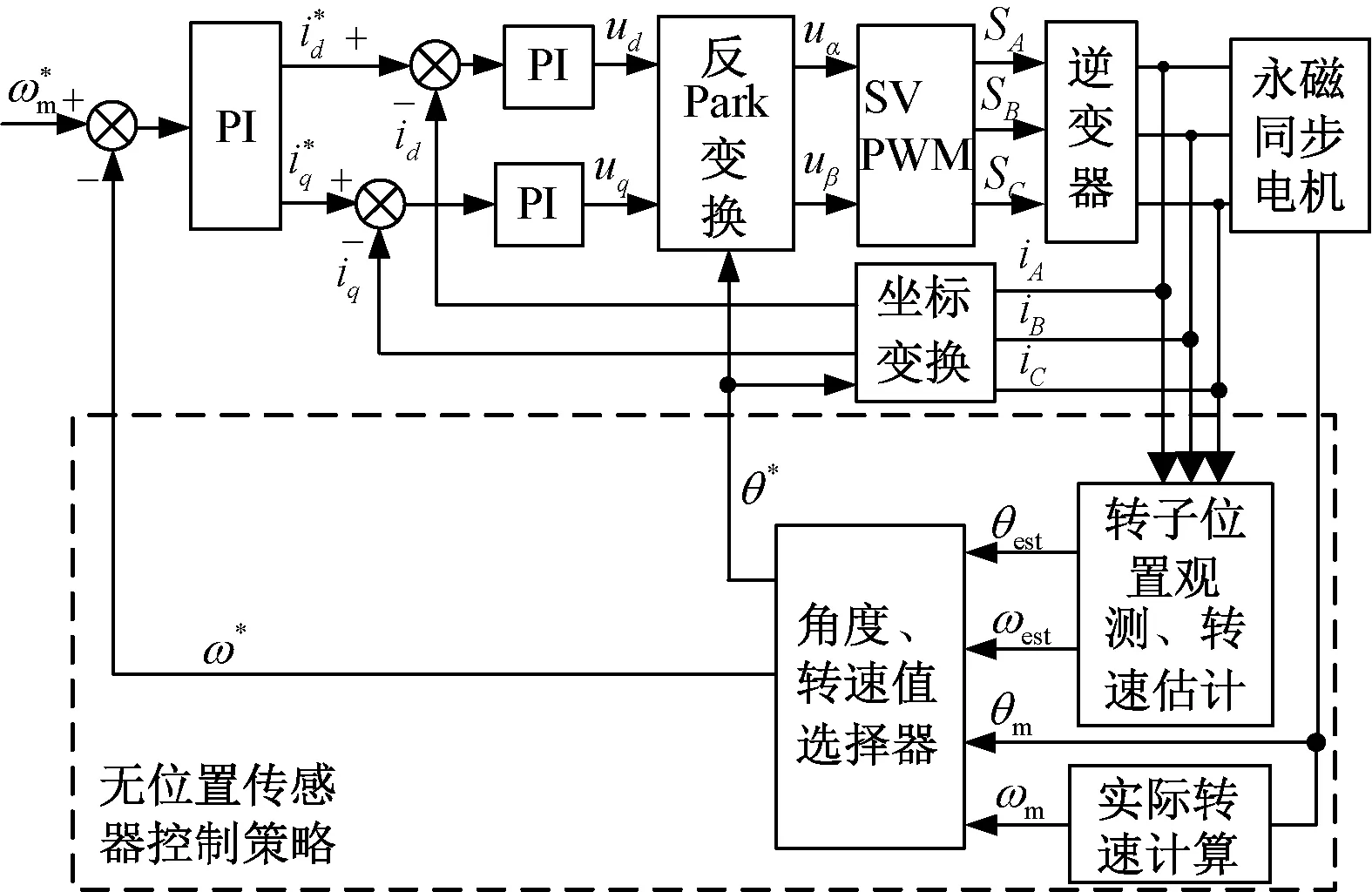
图1 无位置传感器控制算法控制框图

电机控制器采用TMS320F28335微处理器，控制软件采用一个主函数，一个ADC转换中断服务函数。控制软件主函数工作流程图如图2所示。

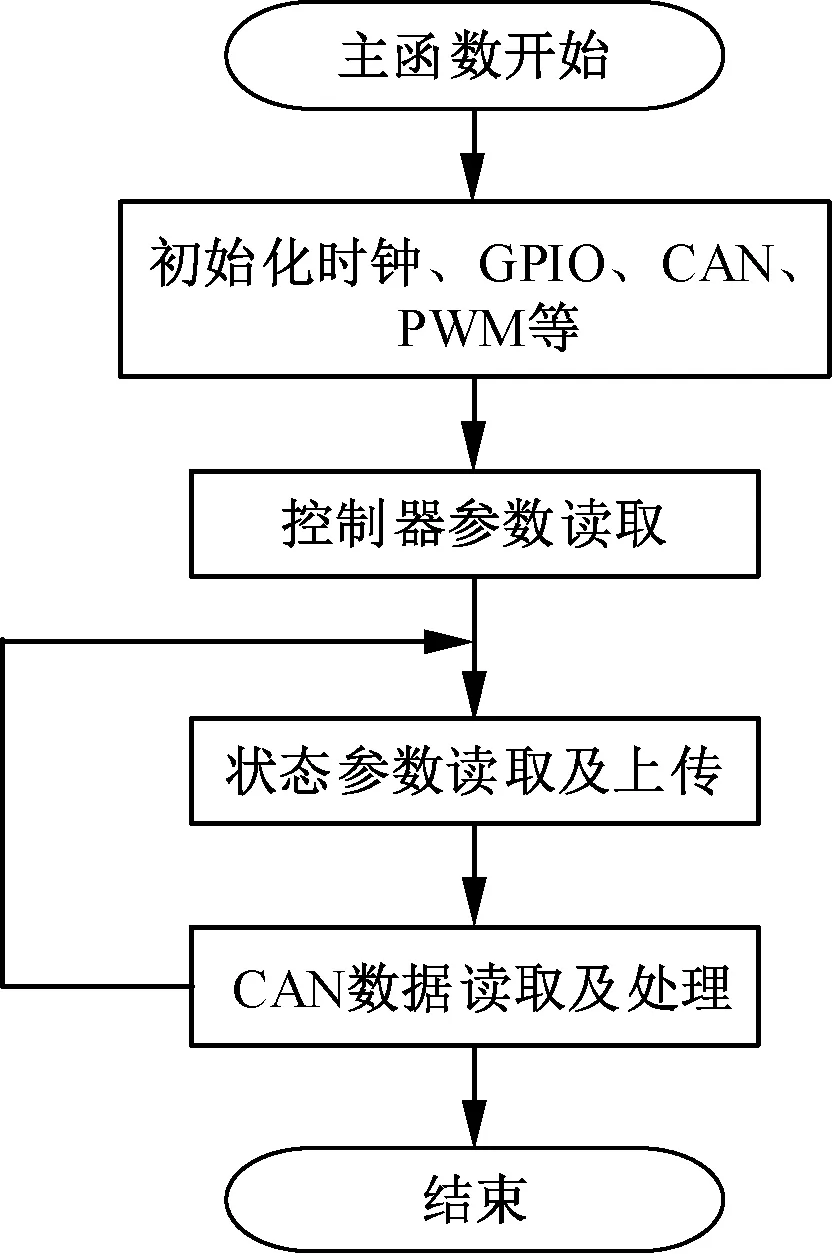
图2 软件主函数工作流程图

软件中断服务函数包括模数换器，即ADC中断服务程序以及PWM故障触发中断服务程序。其中，处理器芯片中的ADC模块每125 μs完成一次对所有AD端口的采样和转换，转换完成后产生ADC中断。PWM故障触发中断在DSP的故障触发引脚TZ2电平拉低时产生，中断服务程序使输出PWM信号被封死，电机停机。ADC中断服务程序的工作流程图如图 3所示。

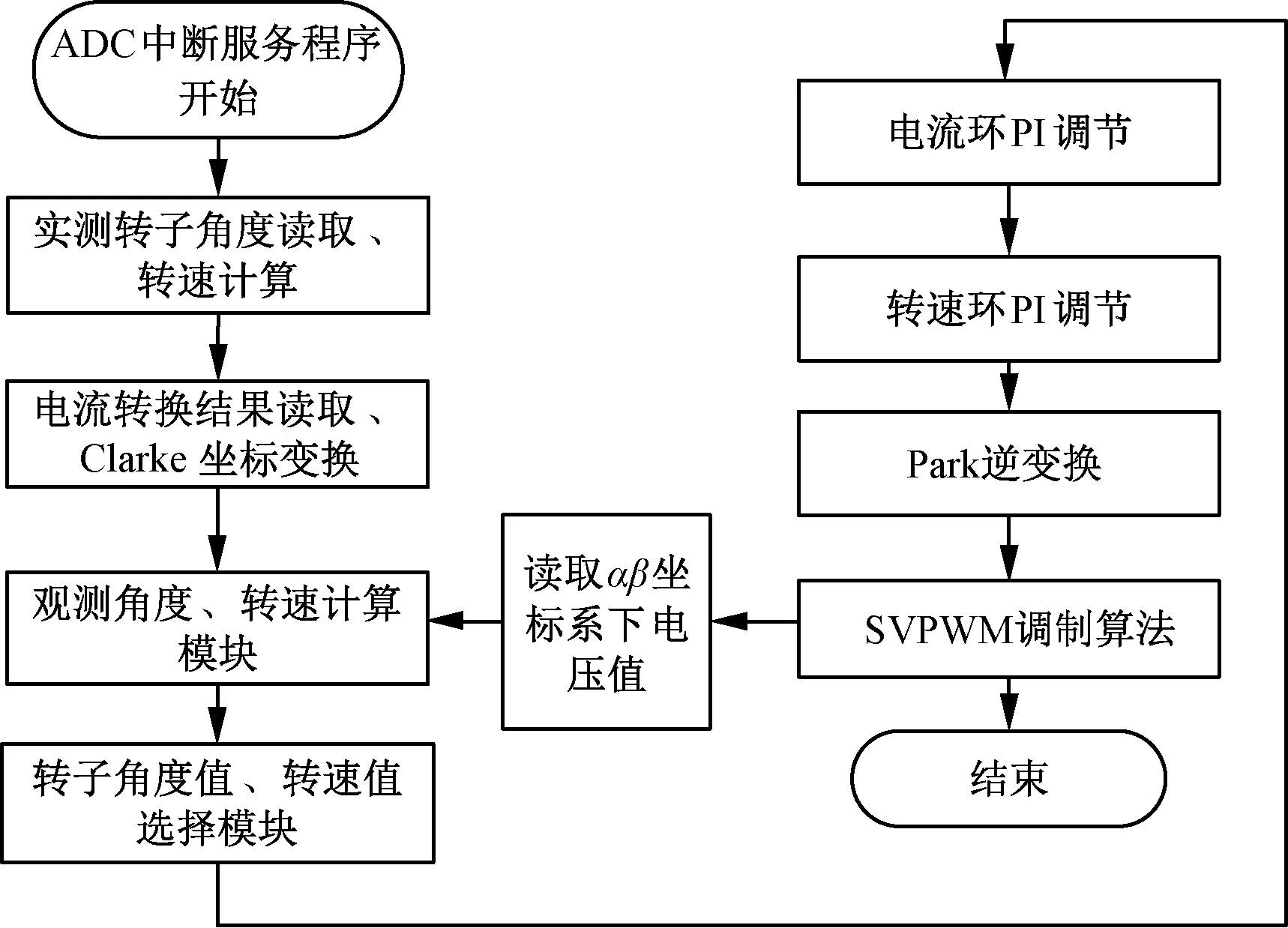
图3 ADC中断服务函数工作流程图

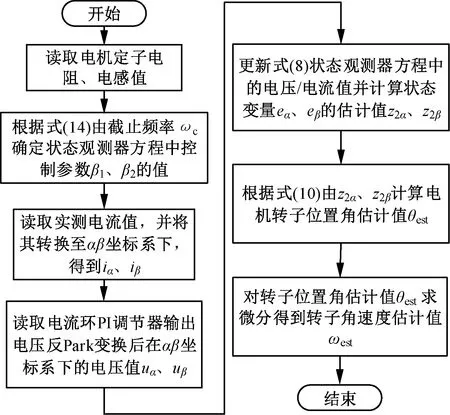
图4 观测角度计算模块工作流程图

如图4所示，在观测角度计算模块中，首先，根据电机额定转速选定反电动势eα至其估计值z2α传递函数的截止频率ωc，根据式(14)由ωc确定状态观测器方程中控制参数β1、β2值；然后，读取实测电流值，并通过坐标变换得到iα、iβ值，并读取αβ坐标系下的电压值uα、uβ，根据式(8)状态观测器方程更新电压/电流值并计算状态变量eα、eβ的估计值z2α、z2β；最后，由式(10)根据z2α、z2β计算电机转子位置角估计值θest，再通过对θest求微分得到转子角速度估计值ωest。

在获得观测角度、转速后，再与位置传感器测量得到的角度、转速信号比较进行选择。在角度值及转速值选择器中，为实现传感器故障与非故障两种模式之间的平滑切换与过渡，要进行低通滤波处理。而工程上最常用的低通滤波处理方式是一阶低通滤波，因此本文的角度及转速值选择器中均采用了一阶低通滤波处理。

角度值选择模块的工作流程图如图 5所示。

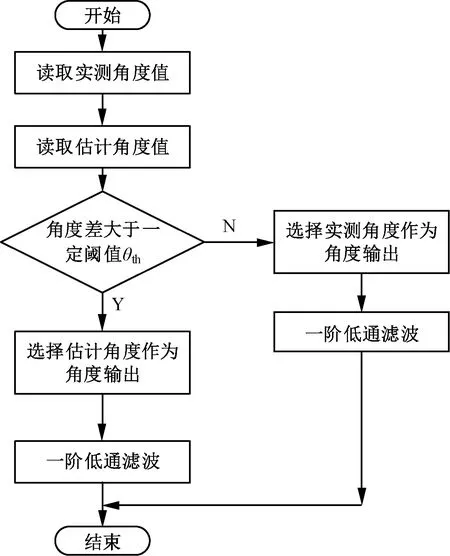
图5 角度值选择模块工作流程

在图5角度值选择模块中，由于位置传感器的实测值精度较高，正常模式时选其作为输出以确保精度。当在一段时间内，转子位置估计值和实测值之间的角度差连续大于一定阈值θth时，认为位置传感器故障，采用估计值作为转子当前角度，再采用一阶低通滤波进行平滑处理；而当二者之差小于θth时，采用实测值作为转子角度，同样采用一阶低通滤波进行滤波平滑处理。该角度阈值θth的选择会影响控制性能。若θth过小，会降低位置传感器正常模式时的控制性能；若θth过大，会降低位置传感器故障模式时的控制性能。实际应用时，可根据以下实验方法确定，先设定角度阈值θth为某一较小值，如30°，若采用该角度阈值后，位置传感器正常模式时的转速波动过大，则将其减小；若位置传感器故障模式时的转速及电流波动过大，则将其增大，直至调整该角度阈值至合适值。如此，通过转速及电流的波动情况即可将角度阈值调整至合适值。

转速值选择模块的工作流程与角度值选择类似。设定判断转速值误差的阈值为额定转速的10%，若大于阈值则选择估计转速作为转速输出，再采用一阶低通滤波进行滤波平滑处理；若小于阈值则选择实测转速作为角度输出，同样采用一阶低通滤波进行滤波平滑处理。

3 实验验证

3.1 实验平台

搭建永磁同步电机控制系统实验台架，对本文的控制算法进行验证。实验测试中采用登奇机电永磁同步电机，被测电机参数如表1所示。

表1 被测电机参数表

由表1可知，电机额定电频率为200 Hz，通常选取截止频率为额定电频率的3倍，则选取截止频率为600 Hz，根据式(14)，由电机参数即可确定控制参数β1，β2值。

实验中系统连接结构图如图6所示。被测电机与负载电机通过联轴器相连，位置传感器采用旋转变压器，即旋变。

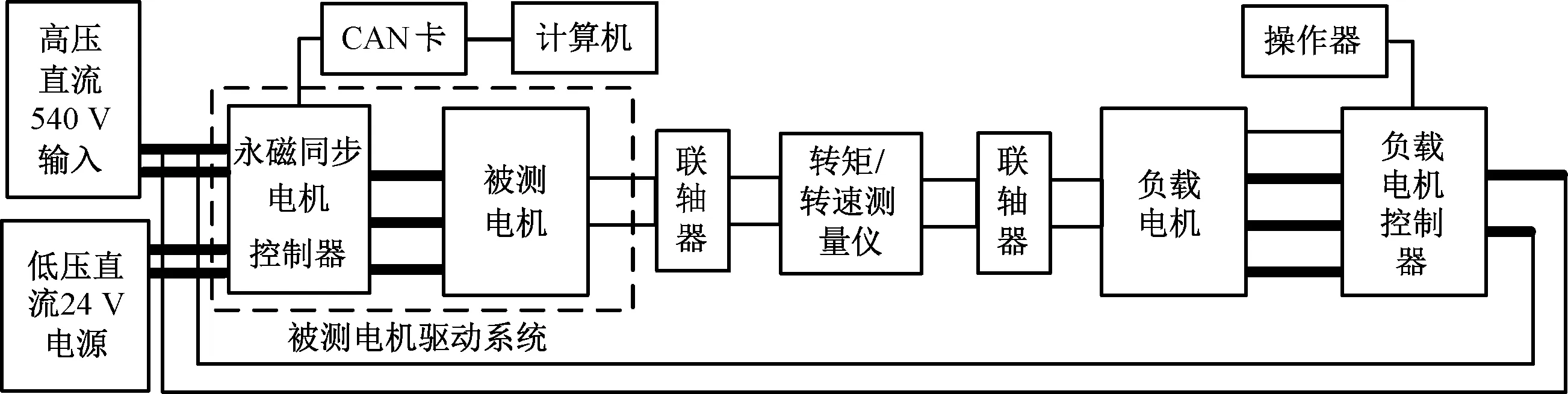
图6 系统试验连接结构图

系统实验照片如图 7所示。

图7 系统实验照片

3.2 实验结果

给定电机转速为额定转速2 000 r/min，将永磁同步电机正常起动，待转速上升至2 000 r/min时，起动负载控制器使得电机转矩约为6.5 N·m，将旋变激励线断开模拟旋变故障，一段时间后再将旋变激励线连接上模拟旋变故障恢复。设置角度阈值为30°，对旋变故障及恢复时的实验结果进行记录，试验结果如下。

电机实测与估计转速波形图如图 8所示，图中，nest为估计转速值，nmea为实测转速值。

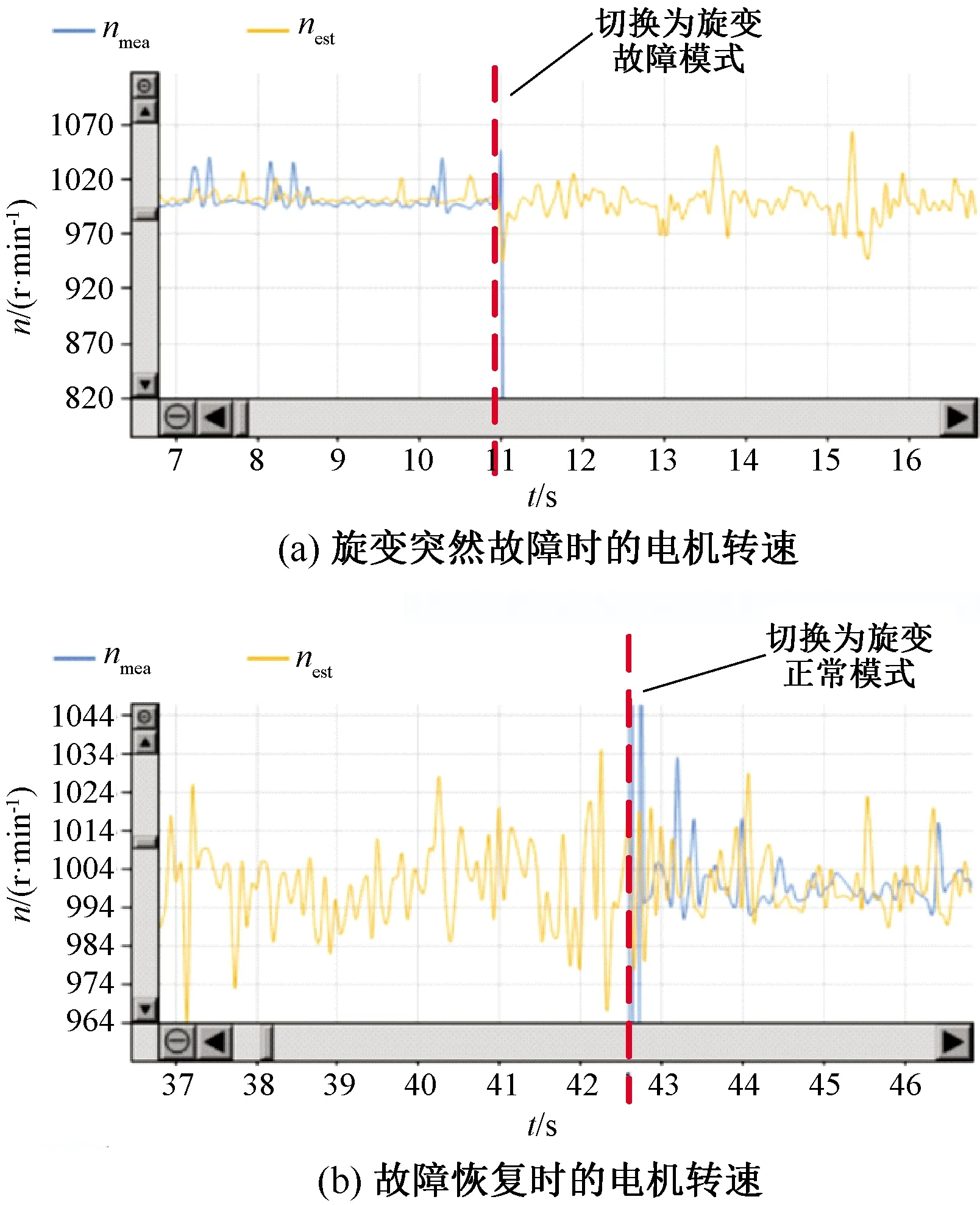
图8 电机转速波形

由图 8可知，在旋变故障与正常模式切换前后系统均能保持稳定。在旋变正常时，电机估计及实测转速与给定值的误差约为2%以内。在旋变故障后，电机转速实测值为错误信号，由于位置保护算法，电机仍正常工作，估计转速与给定值的误差约为5%以内。实现了旋变故障前后电机转速的稳定运行。

估计与实测角度误差值的波形如图9所示。

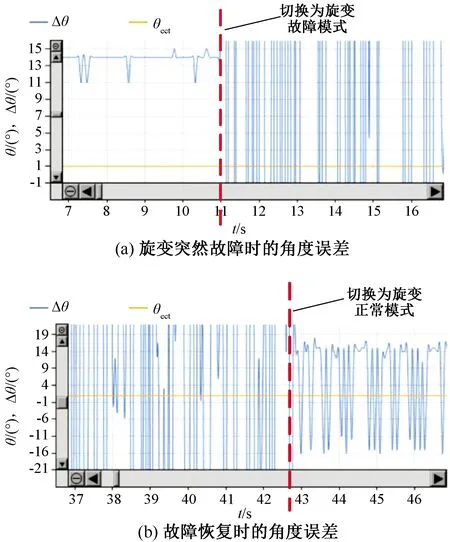
图9 估计与测量角度误差波形

由图9可知，在旋变正常工作时，估计与测量角度的误差绝对值大约在16°的范围内。在旋变激励信号切断后，旋变反馈角度值变为无序干扰信号，估计角度与测量角度误差产生较大的波动，而当旋变恢复正常时，该角度误差又恢复为正常值。

用示波器采集的电机相电流波形如图10所示。

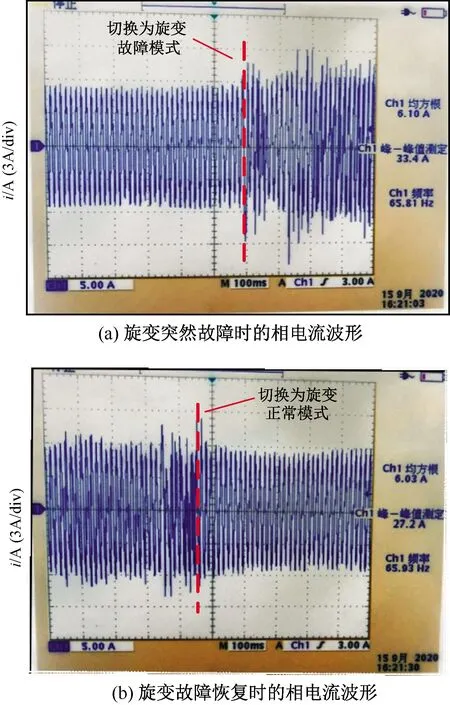
图10 电机相电流波形

由图 10可以看出，旋变正常工作时，电机相电流波形正常，相电流有效值约为6.10 A。当旋变故障后，由于无位置传感器控制算法，电机仍正常工作，相电流有效值约为6.03 A。当旋变由故障切换为正常工作时，电机相电流又恢复至正常状态。实现了旋变故障前后电机相电流的稳定。

由以上可知，采用30°角度阈值时，在位置传感器故障与非故障模式时的转速及电流波动在可接受范围内，本实验中，角度阈值就设置为30°。在旋变故障与正常模式时，系统均能保持稳定运行，实现了永磁同步电机的位置传感器故障保护控制功能。

4 结 语

本文提出了一种将常用于永磁同步电机自抗扰控制中的ESO方法应用于位置传感器故障保护控制中，结合位置传感器控制与无位置传感器控制算法，实现永磁同步电机位置传感器故障保护控制的方法。在位置传感器出现故障时，观测永磁同步电机运行过程中的反电动势，采用扩张状态观测法计算转子角度、转速估计值，替补位置传感器的功能，实现电机的无位置传感器运行，并通过一阶滤波器实现位置传感器故障与正常模式之间的平滑切换。电机对拖实验证明，所提出的方法在位置传感器发生故障及恢复正常时，均能够准确观测永磁同步电机转子位置信息，且运行性能稳定、跟踪性较好，实现了故障模式与正常模式之间的平滑切换。本方法可实现永磁同步电机位置传感器故障保护功能，有效提高系统的可靠性及容错性。