基于改进快速幂次趋近律的PMSM无速度传感器控制

邓 超，王 英

(大连交通大学 电气信息工程学院，大连 116021)

0 引 言

永磁同步电机(以下简称PMSM)由于其结构简单、功率因数高、起动转矩大等优点，在工业、交通以及国防等领域得到越来越广泛的应用[1-2]。

PMSM调速系统的性能与控制算法密切相关，滑模控制是提高系统性能的一个重要方法，系统采用滑模控制可以提高系统的响应速度、增强系统的鲁棒性，但由于其控制的不连续性，在滑模面附近做高频切换运动会产生抖振问题。为了抑制滑模的抖振，文献[3]提出了一种基于传统指数趋近律滑模控制的自适应渐消扩展卡尔曼滤波(AFEKF)控制系统，并在此基础上对趋近律进行了改进,得到的新型指数趋近律使抖振的变速项系数为零，抑制了抖振现象；文献[4]讨论了根据不同的系统状态来对双幂次趋近律中幂次项系数进行调节以提升系统状态逼近滑模面附近的动态品质；文献[5]讨论了双幂次趋近律的滑模控制收敛时间与滑模初始状态的关系，指出双幂次趋近律的特定时间收敛的特点；文献[6]提出了一种基于双曲正切函数的改进型PMSM无感矢量控制系统，推导了基于双曲正切函数的滑模观测器转子位置估算算法。

本文对基于扩展卡尔曼滤波(以下简称EKF)的PMSM无速度传感器控制系统速度环进行了研究，设计了一种快速幂次趋近律改进控制算法，在快速幂次趋近律的幂次项上加入了可以自适应调节的幂次项系数，在加快趋近速度的同时，保留了幂次项的优点，同时将趋近律中的开关函数由双曲正切函数替换，双曲正切函数相比于不连续的开关函数，其变化平缓，不存在突变，在一定程度上削弱了滑模运行过程中的抖振。仿真分析表明，改进型趋近律起动过程更加平稳，转速跟踪波形收敛速度更快且抑制了抖振。

1 基于EKF的PMSM无速度传感器控制系统

图1为基于EKF的PMSM无速度传感器控制系统结构图。

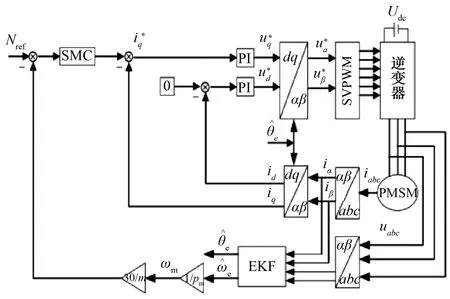
图1 基于EKF的无速度传感器控制系统结构图

PMSM 矢量控制为典型的闭环控制系统，其中包括内部电流闭环与外部转速闭环，外环EKF估算模块的输入为PMSM的参考电压和电流值，输出为估算的转子位置信息以及转速信息。EKF的算法主要可分为两步，首先为对状态矢量的预测阶段，其次为对预测值的校正阶段。

预测阶段分为如下4步：

(1)

(2)

(3)对误差协方差矩阵进行计算：

(3)

(4)

(4)计算增益矩阵K(k+1)：

(5)

校正阶段分为如下2步：

(6)

(7)

同时针对EKF初始协方差矩阵及其初值选择如下：

式中：Q为系统噪声协方差矩阵；R为测量噪声协方差矩阵；P0为初值矩阵。

在本系统中，采用id=0转子磁场定向的控制策略，转速外环使用了滑模速度控制器，趋近律选择使用了快速幂次趋近律[7]，其表达式如下：

(8)

式中：k1>0，k2>0，0<ε<1。

2 改进型快速幂次趋近律

为了进一步提高系统状态变量的运动品质以及更好地抑制抖振，本文在快速幂次趋近律式(8)的基础上设计了一种改进型趋近律，其表达式如下：

(9)

式中：k1>0，k2>0，ε→0+。

依据滑模控制的基本原理，为了保证系统状态空间变量能够从任意不确定的初始状态在规定时间内达到滑模面，需要满足滑动模态的可达性条件，其关系式如下：

(10)

对改进型趋近律进行稳定性判定，验证该趋近律满足Lyapunov稳定性。

选取Lyapunov函数：

(11)

对式(11)求导可得：

(12)

由式(12)可得该改进型趋近律满足Lyapunov稳定性判定，表明在该趋近律作用下，控制系统是逐渐稳定的。

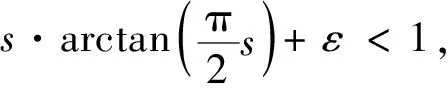
改进型趋近律函数项采用双曲正切函数tanh(s)代替开关函数sgn(s)，其函数图象对比如图2所示。从图2中可以看出，双曲正切函数变化平缓，不存在突变，使得滑模控制器的控制效果更好，系统状态更稳定，能够在一定程度上抑制抖振现象，减小抖振。

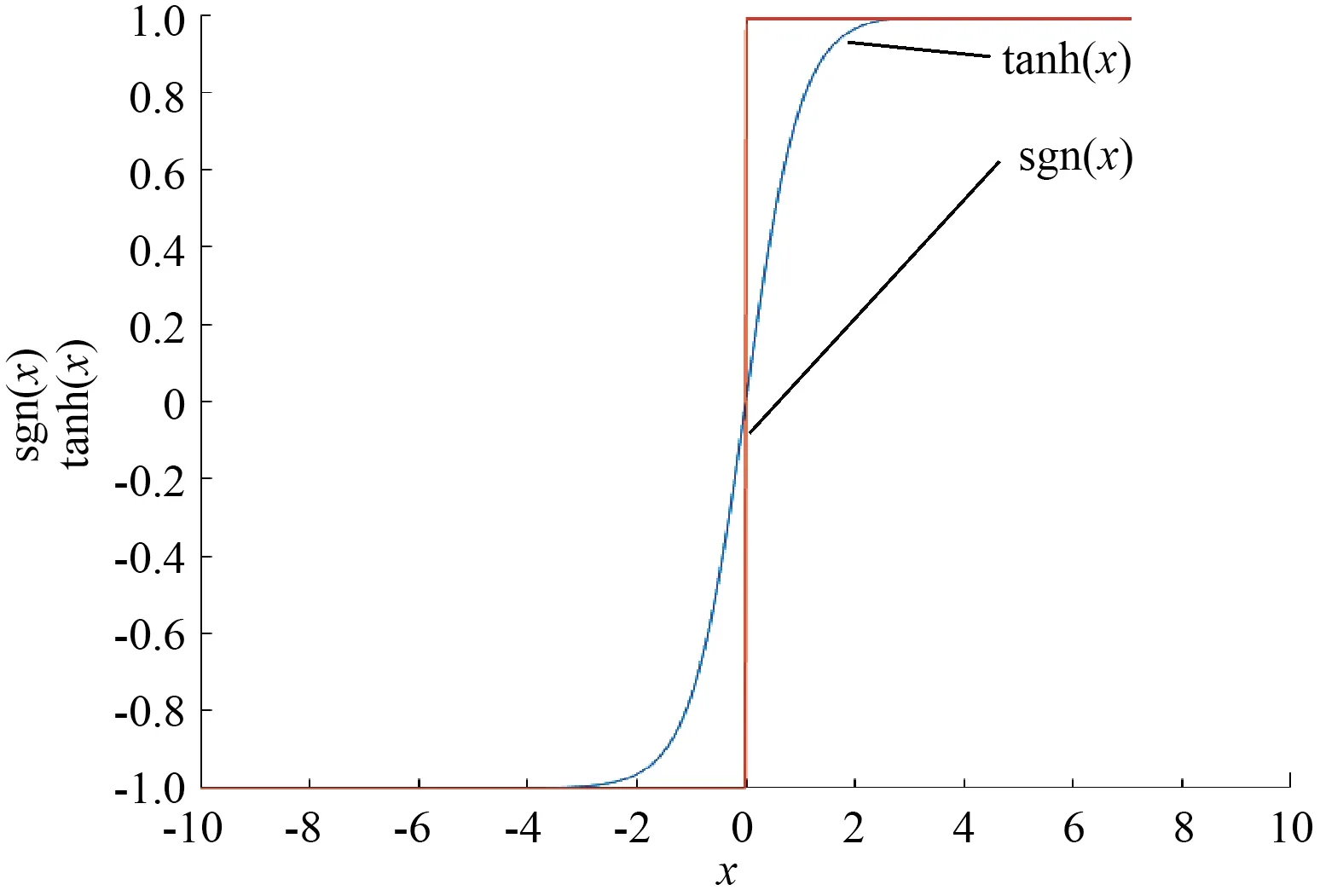
图2 双曲正切函数图与开关函数图

3 滑模速度控制器设计

为了便于滑模速度控制器的设计，验证改进型趋近律的控制效果，本文以表贴式三相PMSM为控制对象，建立d-q坐标系下的PMSM数学模型：

(13)

电磁转矩方程及运动方程：

(14)

式(13)与式(14)中，ud，uq为d，q轴电压；id，iq为d，q轴电流；Te为电磁转矩；TL为负载转矩；ωr为机械转速；p为极对数。

对于表贴式PMSM来说，采用id=0的转子磁场定向控制可取得较好的控制效果，将式(13)与式(14)结合可得到如下数学模型：

(15)

对系统状态变量进行定义：

(16)

式中：ωref为电机的给定机械角速度。将式(16)与式(15)、式(14)结合可得到：

(17)

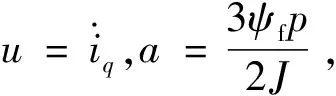
(18)

对滑模面函数进行定义：

s=cx1+x2

(19)

对式(19)求导，即对滑模面求导可得：

(20)

进而将本文提出的改进型趋近律即式(9)与式(20)结合可得到：

(21)

由式(21)可得到iq表达式：

(22)

根据iq的表达式即可在Simulink中搭建滑模速度控制器。

4 仿真结果分析

为了验证改进型趋近律的快速性与改善抖振的效果，基于MATLAB/Simulink搭建了如图3所示的仿真模型。PMSM参数：Rs=2.625 Ω,Ls=0.008 6 H,p=4，ψf=0.173 Wb，J=0.006 kg·m2，预定转速为500 r/min，初始时刻负载转矩TL=0，仿真时间为2 s，在相同条件下，分别对基于快速幂次趋近律滑模控制和基于改进型趋近律滑模控制的无速度传感器控制系统进行仿真，其转速跟踪波形如图4、图5所示。

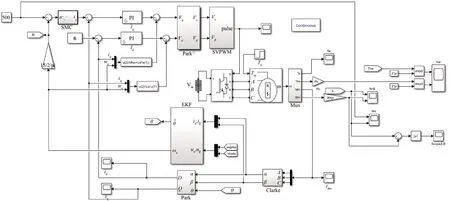
图3 基于改进型趋近率滑模控制的EKF无速度传感器系统

由图4和图5的比较可以看出，在相同的条件下，当电机由静止起动到达预定转速的过程中，采用改进型趋近律的无速度控制系统转速跟踪波形能够更快地收敛到预定转速，收敛时间由0.226 s减小到了0.143 s，收敛时间缩短了0.086 s，收敛速度提高了36%，表明改进型趋近律相比于快速幂次趋近律而言，可以加快转速跟踪波形的收敛速度，验证了该趋近律的快速性。

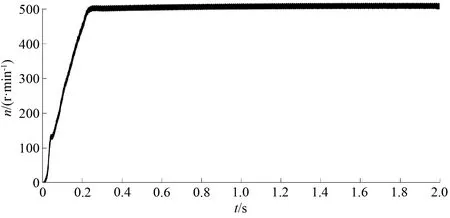
图4 快速幂次趋近律滑模控制的EKF转速跟踪曲线

图5 改进型趋近律滑模控制的EKF转速跟踪曲线

图6为改进型趋近律的无速度控制系统对转子位置的跟踪图。可以看出，转子位置的实际值与转子位置的估计值几乎重合，实现了较好的跟踪效果。

图6 改进型趋近律滑模控制的转子位置跟踪图

图7、图8为转速跟踪波形局部放大图。可以看出，在截取的相同时间内，基于改进型趋近律的无速度控制系统稳态运行时，转速跟踪波形抖振现象得到缓解，验证了改进型趋近律函数项采用双曲正切函数相比于开关函数而言，能够缓解转速跟踪波形的抖振，使得跟踪波形更加稳定。

图7 快速幂次趋近律滑模控制的转速跟踪放大图

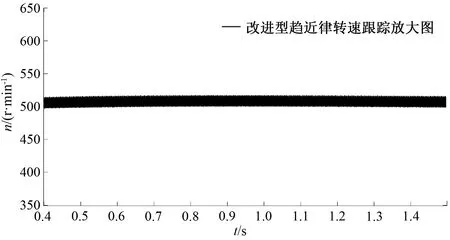
图8 改进型趋近律滑模控制的转速跟踪放大图

5 结 语

本文为了加快滑模控制的趋近速度和改善抖振，设计了一种基于改进型趋近律的滑模速度控制器，并通过仿真验证了改进型趋近律趋近速度的快速性以及对抖振的抑制能力，使得应用改进型趋近律滑模控制的EKF无速度控制系统能够满足实际控制性能的需求。