风致涡激共振对永磁直线发电机电磁特性的影响

龚曙光，蒋自强，谢桂兰，张建平，卢海山

(湘潭大学 机械工程学院，湘潭 411105)

0 引 言

风能是当今世界使用最为广泛、清洁的能源之一，其利用方式也多种多样，风力发电机是风能最普通的使用方式。近年来，涡激共振压电的研究是风能利用的一个热点[2]，但是该方式常用于微型发电，具有发电量小的局限性。而传统带桨叶的风力机具有运输、制造、维修困难等问题且会危及飞行的鸟类。基于此，本文提出一种新型的风能利用装置——无叶片风力发电机。与传统有叶片的风力机相比，无叶片风力机具有制造成本低、结构简单、易加工和维修方便等优点，同时也为未来分布式发电带来活力。

永磁发电机相对于励磁发电机具有更高的发电效率和节能效果，其具有结构简单且可靠性、稳定性高等优点[3-4]。如文献[5]提出了一种新型的无铁心的直线发电机，探讨了其在定常速度下的电磁特性，并提高了系统稳定性，但其忽略了发电机的电压幅值和输出功率；文献[6-7]研究了永磁直线发电机在匀速下的电压、功率、边端力等电机特性。除此以外，许多学者也致力于研究直线发电机在简谐运动下的电磁特性。如文献[8-9]推导了调制型永磁直线发电机在正弦速度下的电动势表达式，并应用于波浪能发电；文献[10]给出了单相发电机在正弦下的运动方程和发电机的输出方程，通过实验测得在最大负载运行下发电机的输出效率可达83.92 %；文献[11]通过对永磁直线发电机在简谐运动下的理论推导，找出了适应电机性能的振动区间，并得到了仿真验证；文献[12]探讨了直线发电机在自由活塞式运动时的电磁特性，比较了矩形截面和工字形截面的永磁体对发电机性能的影响；文献[13]通过实验分析了发电机在空载和负载条件下的电机输出特性。文献[14]、文献[15]研究了永磁直线发电机在不规则正弦运动时的电磁特性，推导了波浪对浮子的作用力，并得到了验证。

目前永磁直线发电机主要针对匀速运动或简谐运动开展研究，尽管也对不规则的正弦运动有所探讨，但其应用场景主要是用于波浪能发电，而波浪能的重力波周期一般为5～10 s(海岸工程)。相反，无叶片风力机捕能柱的风致涡激振动是一种高频低振幅振动，且其振动也呈现为非周期性。基于无叶片风力机捕能柱的振动特性，本文首先对永磁直线发电机进行了结构设计，并对其空载特性、负载特性进行仿真分析，采用反正切与正弦函数的乘积逼近发电机在涡激共振下的运动轨迹，以探讨捕能柱的来流风速和振幅对发电机电磁特性的影响。

1 无叶片风力机原理

无叶片风力发电机主要由捕能柱、转换装置与发电机组成，其原理简图如图1所示。捕能柱在风致涡激振动下产生横向摆动，转换装置则将捕能柱的摆动转换成直线运动再传给直线发电机，永磁直线发电机的功能是将机械能转化为电能，为了方便安装与维修，其位于风力发电机的最下端。

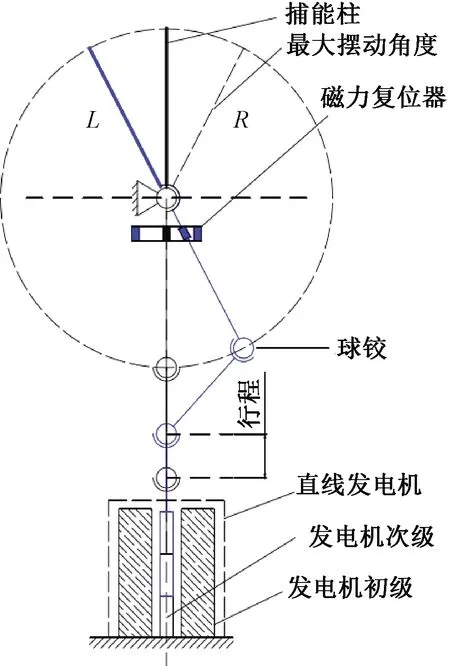
图1 无叶片风力发电机原理图

在风致涡激振动中，无叶片风力机捕能柱获得的风能输入功率：

(1)

式中:ρ为空气的密度；U为风速；D为柱体直径；H为柱体高度。

设捕能柱摆动的最大角度为θmax，稳定摆动的角度为θ1，经转化后其最大行程为Lmax，稳定时行程为L。本文假定无叶片风力机的设计风速为6.0 m/s，其柱体直径为0.2 m，高为1.3 m。由式(1)即可得到风能的输入功率为36.3 W。

2 圆筒形永磁直线发电机

2.1 电机结构

永磁直线发电机的结构如图2所示，因为发电机的次级是作上下运动，为减轻次级质量，方便电能传输，将发电机结构设计成外部长初级、内部短次级。永磁直线发电机由三相初级铁心、三相绕组、次级铁心和次级永磁体组成。为了方便制造和获得较大的气隙磁密，永磁体采用表贴式，且沿着径向方向充磁，相邻永磁体充磁方向相反。三相绕组采用模块化饼式绕组，单独加工成型后嵌入定子槽内。

图2 永磁直线发电机二维结构图

此外，发电机的运行效率和成本是电机设计过程中需要考虑的重要因素，而行程的长短又与发电机的运行效率和成本有直接关系。因此，结合额定风速下捕能柱在涡激共振时的振幅，以及其输入功率为36.3 W，在假定设计电压为12 V，通过磁路设计，得到发电机的主要参数，如表1所示。

表1 永磁直线发电机的参数

2.2 匀速下电机空载特性

通过仿真分析得到发电机空载时的磁通线分布如图3所示，图4为发电机空载磁感应强度的云图。

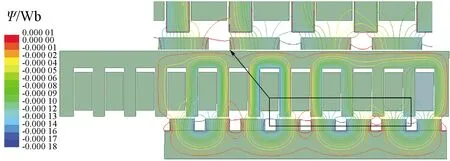
图3 空载磁通

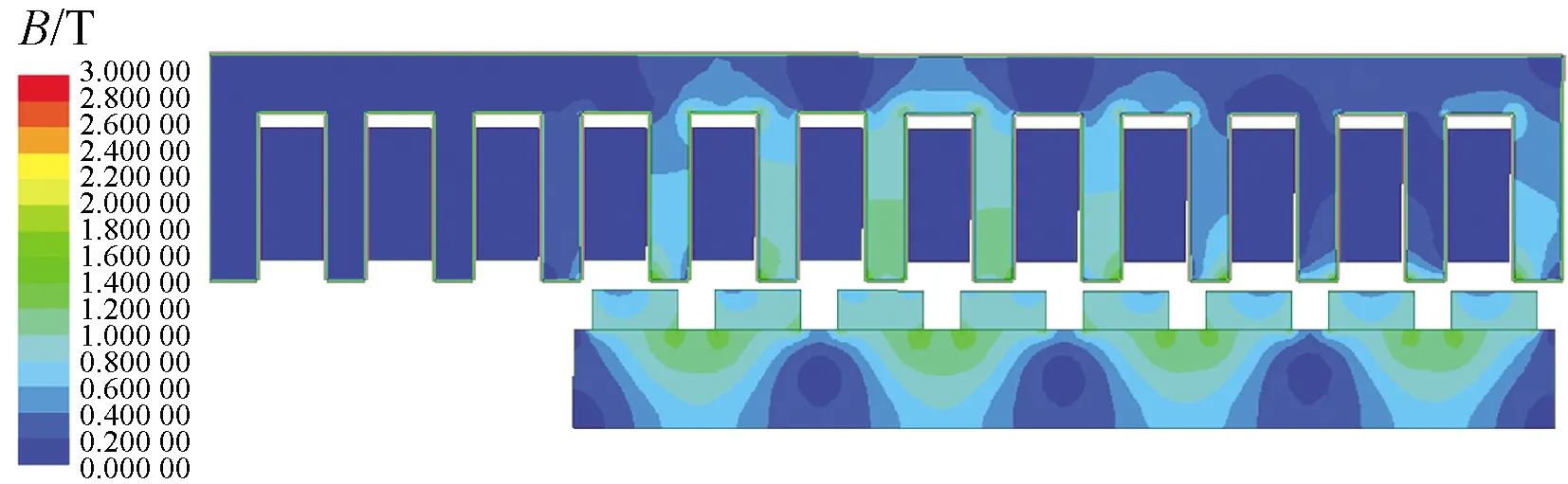
图4 空载磁密

从图3可看到，磁力线主回路从N极发出，经过气隙进入定子齿，再经过定子轭后从下一个定子齿流出并再一次进入气隙，然后通过相邻极性相反的磁极，最后从次级轭部回到原来的磁极。即除了磁力线主回路之外，存在着另外两条磁路，一条是从永磁体N极出发，直接从气隙进入到相邻的下一个磁极，再通过次级轭回到原永磁体；另一条是从N极出发，经过初级齿后流入到初级槽，再从初级槽流入气隙，然后通过相邻磁极和次级轭回到该永磁体的S极。

从图4可知，初级齿部平均磁感应强度为1.09 T，在齿顶处的两端其磁感应强度较大；初级轭部平均磁感应强度为0.55 T，在定子齿尖端处存在极小区域内的磁密过大，但是饱和程度不大，所以从总体来看可忽略磁饱和现象，符合设计要求。同时，由于发电机的能量转换是在气隙中完成，故气隙的长度和磁场强度的变化规律对发电机的性能有着重要影响。

图5显示了发电机在t=0时径向气隙磁密的分布。由于发电机的开断影响，气隙磁密在永磁体N极和S极不够对称，气隙磁密的最大值为0.92 T，平均磁密为0.56 T；正对永磁体两端的气隙磁密高于永磁体中间部分，这是因为在一定范围内，永磁体极面面积越大，则极面中心的磁感应强度越低于其周边的磁感应强度。

图5 t=0时刻空载气隙径向磁密

对气隙磁密进行傅里叶分解，其谐波分布如图6所示。从图6可知，气隙磁密的谐波次数较多，气隙磁密的基波幅值为0.788 7 T，波形畸变率为17.5%。

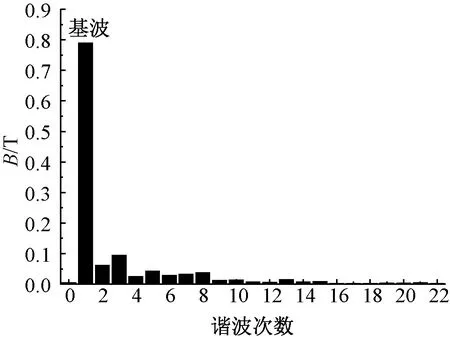
图6 空载气隙磁密FFT

发电机的感应电动势如图7所示。从图7可知，三相电压幅值分别为18.57 V、18.38 V、18.41 V，与设计的电压值基本吻合，证明所设计的电机是合理的。通过对电压谐波分析可知，其三相基波幅值分别为18.50 V、17.82 V、17.90 V，平均波形畸变率为7.5%。

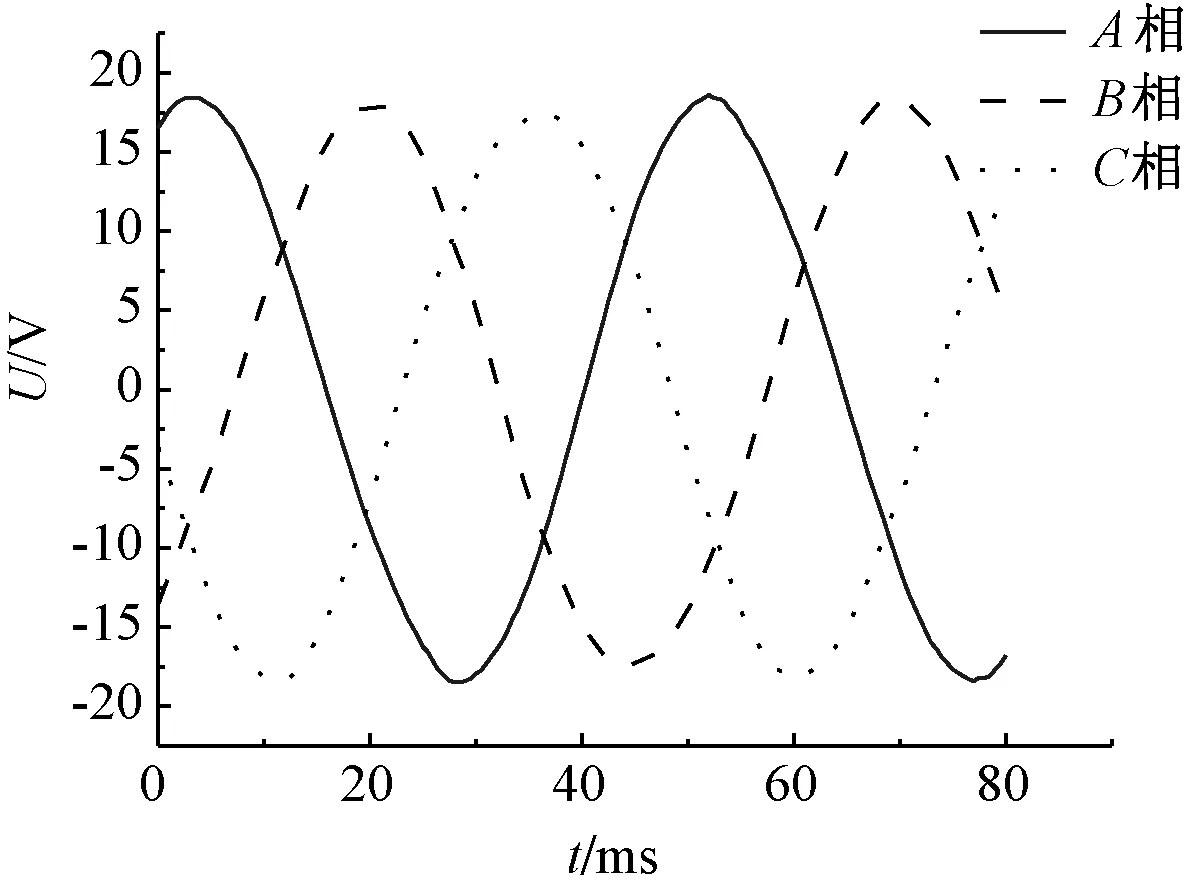
图7 感应电动势

2.3 负载特性

发电机的负载特性是衡量发电机性能的关键因素。本文中的负载工况为纯电阻电路，在次级速度为0.5 m/s下计算了不同负载工况下的电压、电流、功率和效率。

图8显示了发电机输出功率、效率与负载的变化曲线。从图8可知，输出功率随负载的增大呈现先增大后减小的趋势，这是因为随着负载的增大，负载端电压逐渐增加，当负载继续增大时，电压增加会趋于平缓，而由电路理论可知，当电压保持不变时，纯电阻电路中的输出功率随负载的增大而减小。同时在纯电阻电路中，电机的损耗主要是铜耗和铁耗，当电阻增大时，电机电流下降，绕组铜耗也随之降低，而铁耗在低频电磁场中所占比例不大，因此电机的效率随着外电阻电路的阻值增大而增大。图8的最大输出功率为114.5 W，最大效率为89.77%。

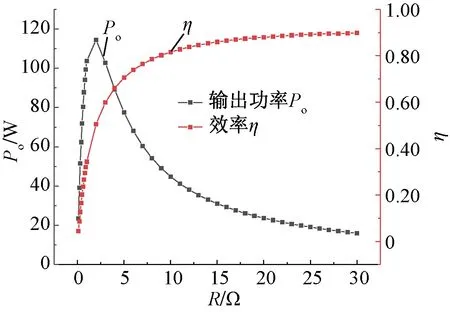
图8 输出功率、效率随负载的变化

发电机的负载电压如图9所示。从图9可知，在纯阻性负载状态下，其三相电压幅值分别为17.91 V、17.96 V、17.88 V，相比空载感应电动势分别小了0.58 V、0.42 V、0.53 V，且三相的对称性良好。

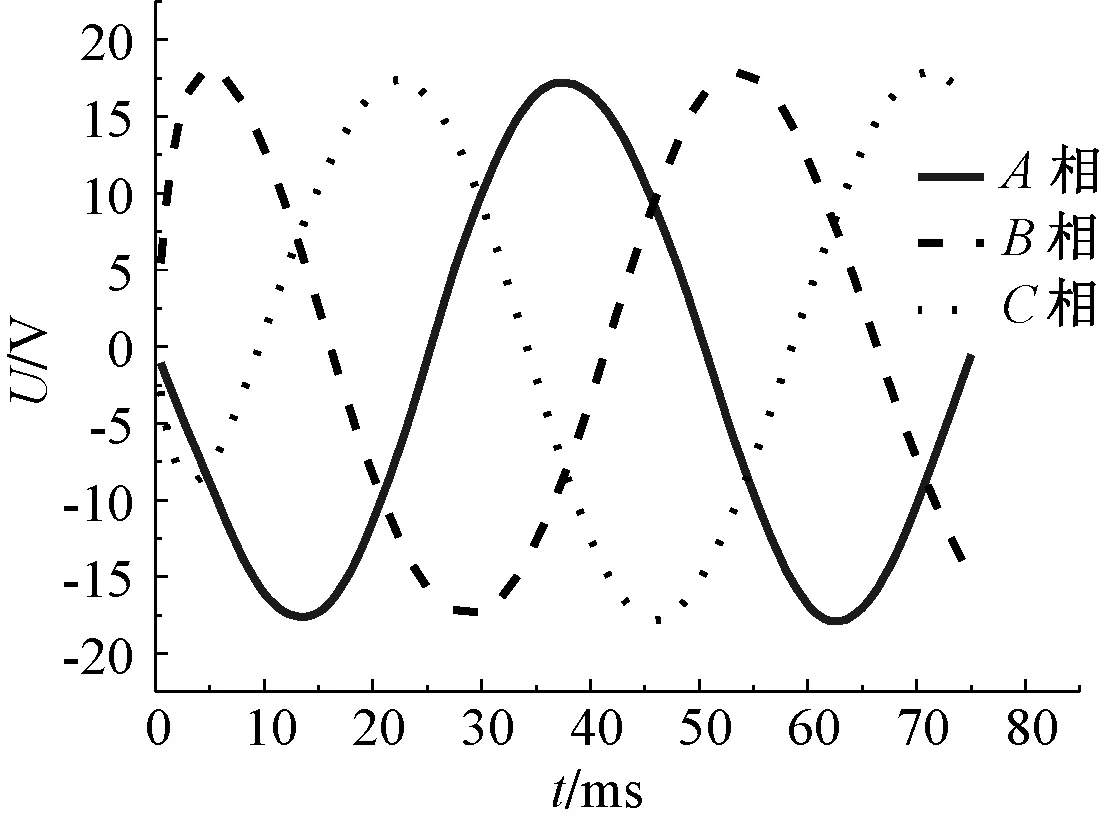
图9 负载电压

由于外电路采用了纯阻性负载，故其电流波形相位与电压一致，数值上符合欧姆定律。为了获得较好的电机输出性能，兼顾功率和效率，现选取外电阻为12 Ω，图10显示了在电阻值为12 Ω时，其电压、功率和效率随次级速度的变化。

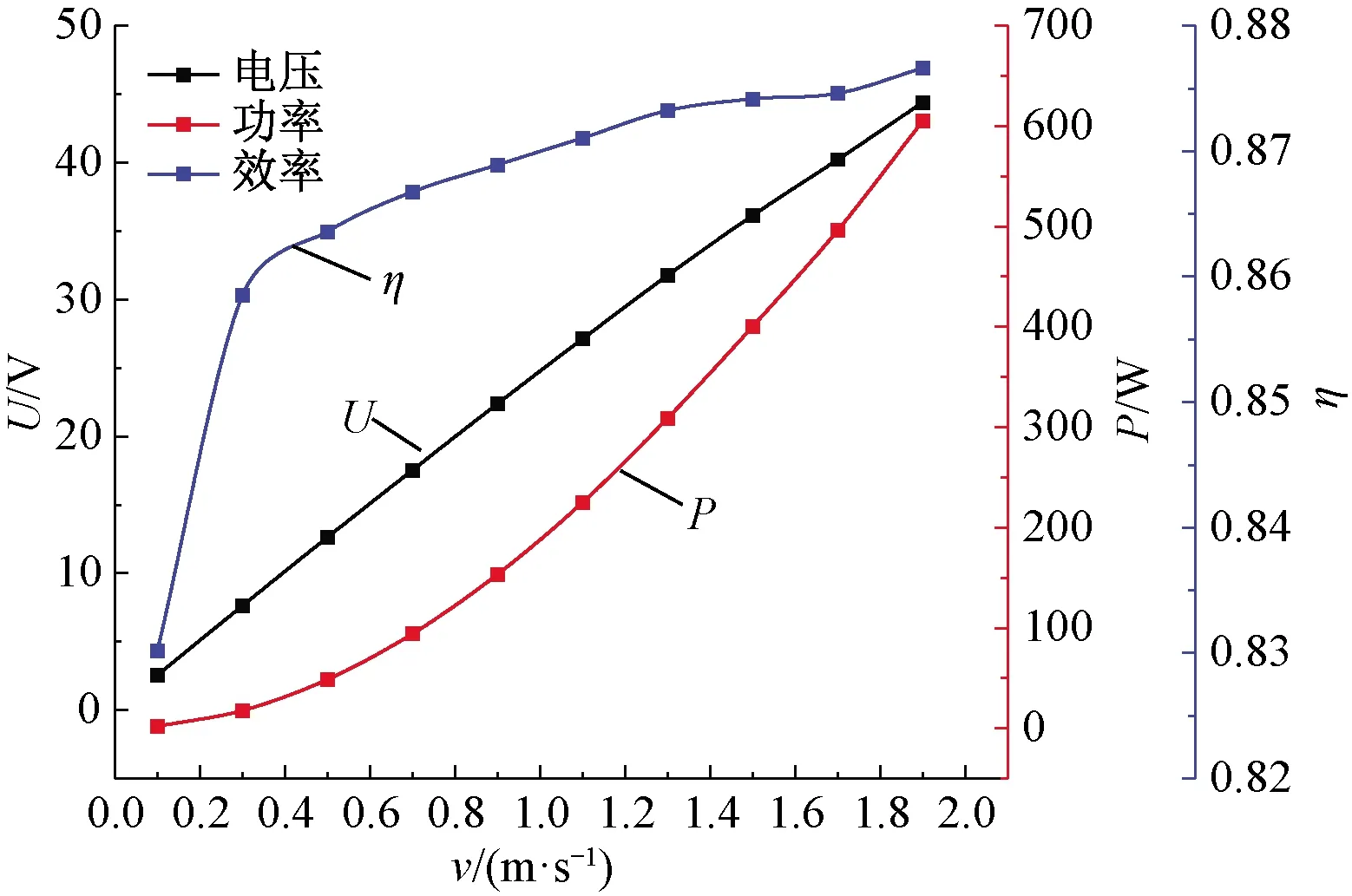
图10 电压、功率和效率随次级速度变化

从图10可看出，电压与输出功率随次级速度的增加而增加，这是由于在纯电阻电路中阻值不变时，当速度增大其输出电压增大，输出功率也随之增大，且电压与速度为线性关系，而输出功率与速度的二次方成正比，因此输出功率的增加趋势如同抛物线。同时，电机的效率随着速度的增大逐渐趋近于88%，这是因为随着速度的增大，电机的损耗也逐渐增大。

通过计算得到本文所设计发电机的体积功率密度为59.71 kW/m3，该值与文献[8]实验测试值57.27 kW/m3相接近，这进一步说明本文所设计的直线发电机是可行的。

3 风致涡激共振的影响

捕能柱在来流风作用下会产生涡激振动，随着来流风速的增大，其涡激频率会逐渐接近系统固有频率，而使捕能柱产生共振，此时捕能柱的横向摆动角度(也可称为振幅)达到最大值，其风速区间也称为“锁频区间”。然而在自然界中，风速一般处于不稳定状态，捕能柱的横向摆动也处于一个非稳定的简谐运动，因此本文主要针对来流风速和振幅对发电机性能的影响进行分析。

3.1 风速的影响

本文无叶片风力机的设计风速为6 m/s，在 4～8 m/s间选取多个风速，通过计算得到不同风速下次级速度的变化曲线，如图11所示。

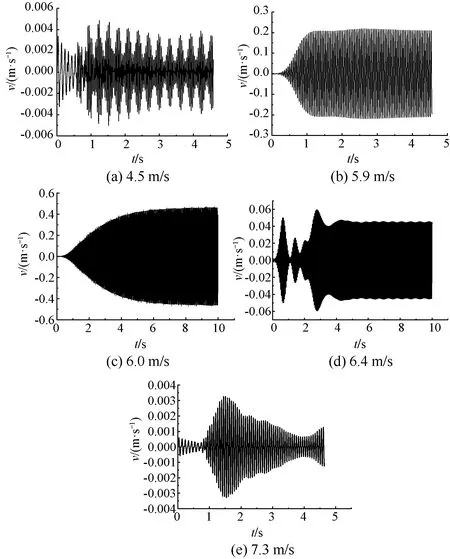
图11 不同风速下次级速度变化曲线

从图11中可看到，随着来流风速的增大，次级速度幅值出现了先增大后减少的趋势，其变化呈现出了不规则的简谐运动，直到来流风速达到设计风速时，次级速度幅值达到最大，同时在“锁频”风速区间，次级的上下振动频率也趋于稳定。

图12给出了永磁直线发电机在设计风速下的瞬时最大输出功率和平均输出功率。从图12可看到，当风速为6 m/s时，瞬时最大输出功率可达35.62 W，平均功率达到15.95 W。

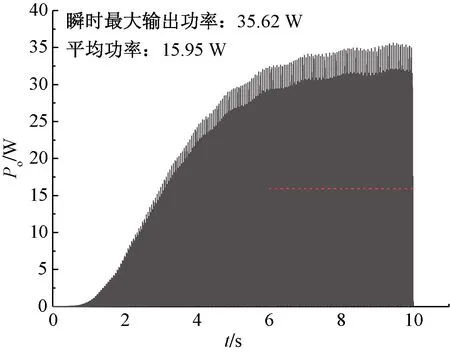
图12 设计风速下发电机的输出功率

按与图12类似的计算方法，可得到不同风速下发电机的平均输出功率与效率，如图13所示。

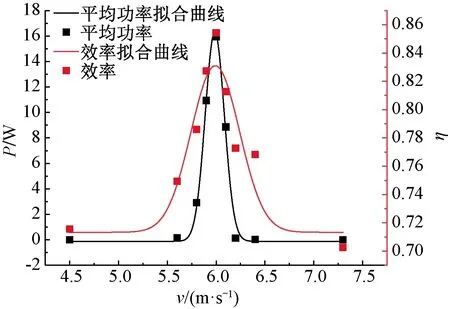
图13 不同风速下发电机输出功率和效率

图13中，发电机的输出功率与效率均随风速的增大呈现先增大后下降的趋势，特别是当来流风速处于共振区间时，发电机的输出功率和效率达到最大，即其最大平均输出功率为15.95 W，最大效率为85.44%。这也意味着当风速处于共振区间时，本文所设计的发电机具有良好的输出特性。

同时，发电机三相电压随风速的变化如图14所示。从图14可知，发电机在捕能柱锁频区间内具有较高的电压，当捕能柱处在共振状态时，其具有较大的摆动频率和振幅(摆动角度)，使得发电机次级的运动速度更大。同时由于次级运动速度不恒定，发电机的次级运动规律和磁场分布匹配不佳，并且受发电机两端开断的影响，发电机的三相电压不对称，此时发电机的三相电压的幅值分别是5.03 V、10.30 V、7.75 V。当风速值离开共振区间后，捕能柱处于高频低幅摆动，故电压下降。

图14 不同风速下发电机输出电压

3.2 振幅(摆动角度)的影响

设振幅倍数以设计风速下的次级运动行程为基频，当发电机的次级运动频率接近系统固有频率即10 Hz时，次级运动的最大振幅为7.5 mm。

设次级运动位移与时间的关系近似采用正弦函数与反正切函数的乘积逼近，即有：

x(t)=A(t)sin2(2πft)

(2)

式中:x为位移；t为时间；A(t)=Aarctan(P(t))为振幅随时间变化的反正切函数；P(t)为t的多项式；f为频率。

对位移求导可得到次级运动速度与时间的关系：

v(t)=A′(t)sin2(2πft)+A(t)2πfsin(4πft)

(3)

由法拉第电磁感应定律可知，感应电动势表达式：

(4)

式中:ψ为磁链，且有：

(5)

式中:ψm为最大磁链；τp为极距。

将式(2)、式(3)、式(5)代入到式(4)中，可得感应电动势表达式：

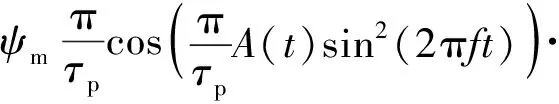
[A′(t)sin2(2πft)+A(t)2πfsin(4πft)]

(6)

由于本文以纯电阻电路为研究对象，故其输出电压表达式：

U=E-Ir

(7)

式中:I为电流；r为内阻。

当P(t)选取为线性函数、二次函数和指数函数时，其在不同振幅倍数下的电压值与有限元的仿真结果对比，如表2所示。

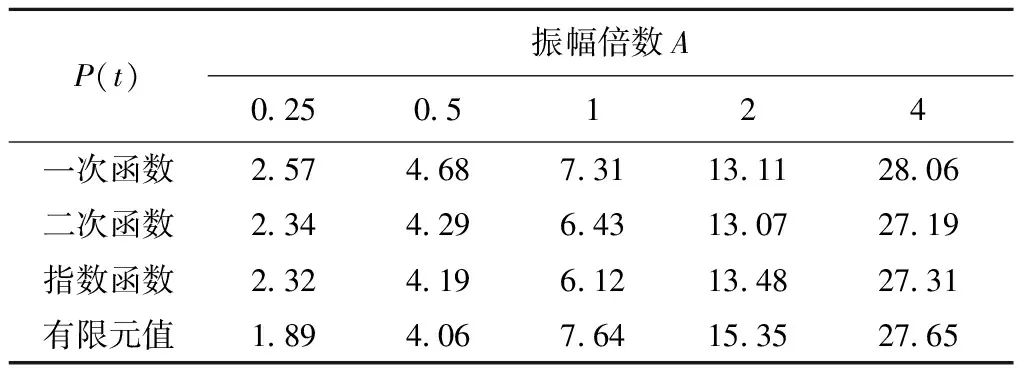
表2 不同变量函数下的电压 (单位：V)

从表2可知，线性函数在1倍振幅和4倍振幅处、二次函数在0.5倍振幅和4倍振幅处、指数函数在0.5倍和4倍处的结果与仿真结果相接近，分析其均方误差，线性函数、二次函数与指数函数的均方根差值分别为1.108、1.194、1.106。误差较大的原因是初始数据的正弦度不够好，并且相邻振幅之间并不是逐渐上升，中间有少许畸变，综合比较选取指数函数为振幅函数的变量函数。

图15显示了永磁直线发电机电压、推力随次级运动振幅倍数的变化曲线。振幅倍数对发电机输出功率和效率的影响如图16所示。

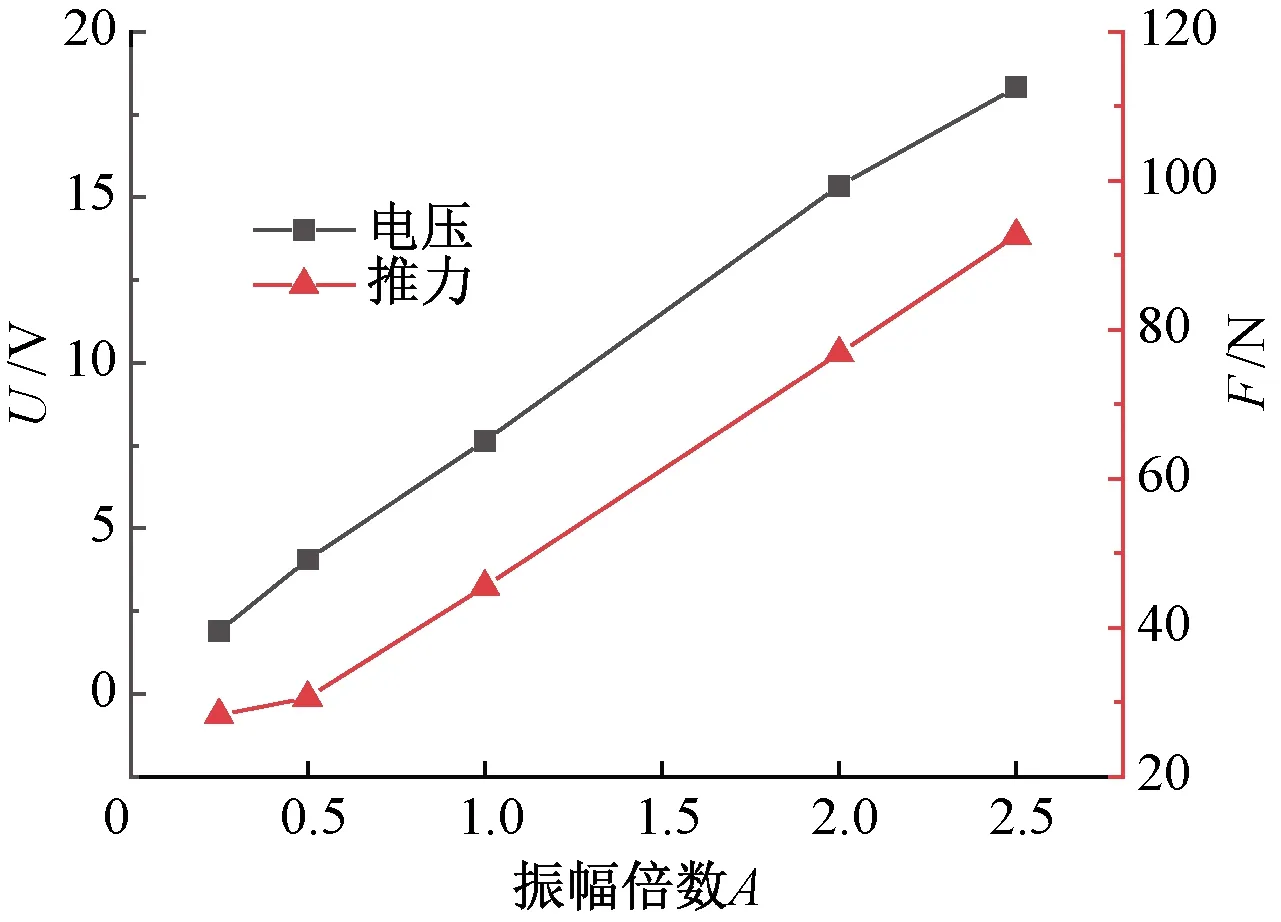
图15 不同振幅下发电机输出电压和推力

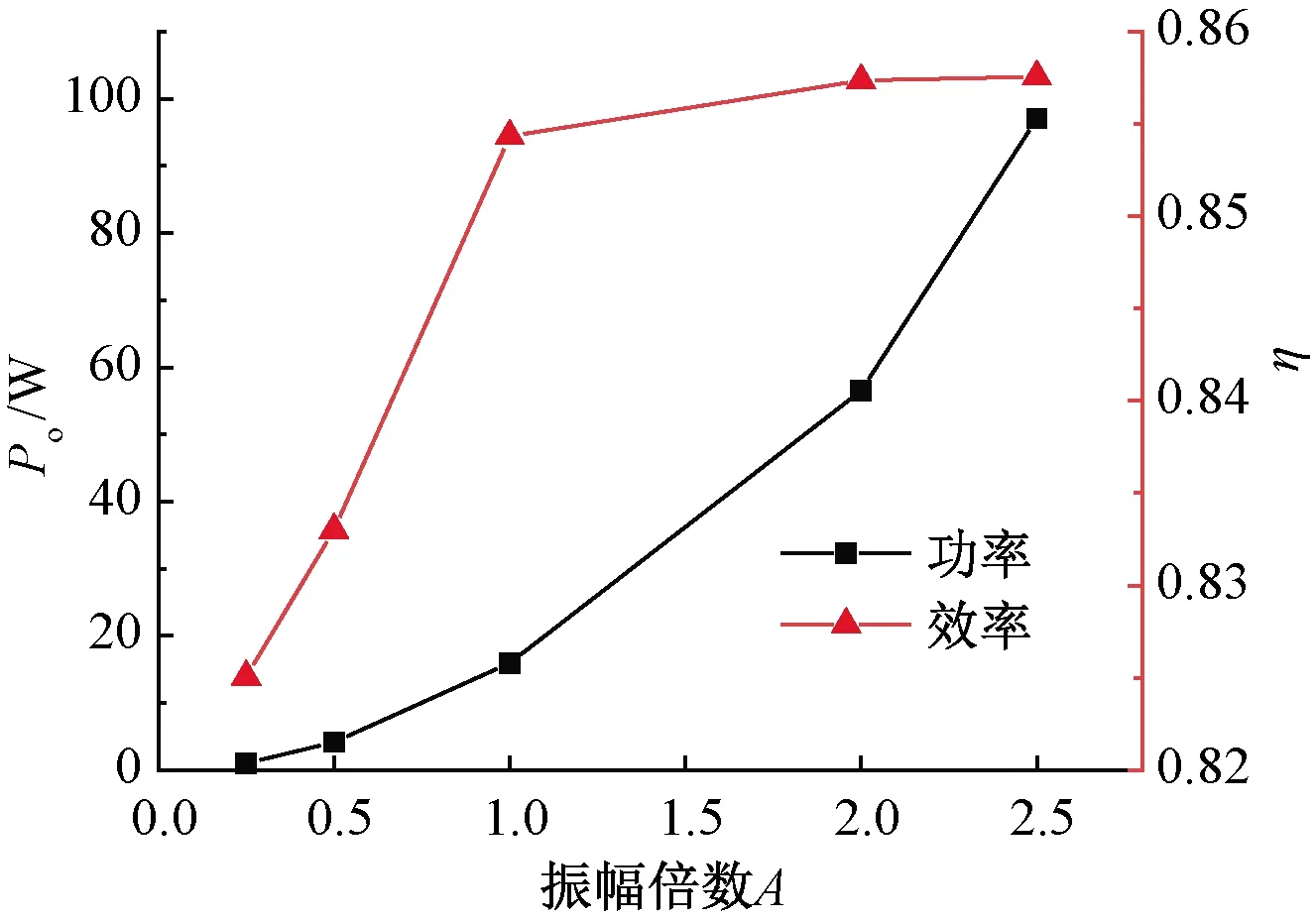
图16 不同振幅下发电机输出功率和效率

从图15可知，当振幅增大时，发电机的电压和电磁推力随之增大，且电压的增长近似为直线，符合电动势的变化趋势。

从图16可知，发电机的输出功率随振幅倍数的增大而增大，且在2.5倍振幅处有最大值97.06 W；发电机的效率同样随着振幅倍数的增加而增加，但当振幅倍数由1.0增大到2.5时，其效率将由85.44%增大到85.76%，即其增幅变缓，这是因为随着电压的增加，发电机损耗增加得更快，其效率逐渐趋于某一定值。

4 结 论

本文基于无叶片风力机捕能柱的涡激振动特性，完成了永磁直线发电机的设计，在可行性得到验证的基础上，探讨了捕能柱的来流风速和振幅对发电机电磁特性的影响，得到的结论如下：

(1)所设计的永磁直线发电机能够与给定参数下的无叶片风力机相匹配。

(2)当来流风速达到设计风速即6 m/s时，发电机的瞬时功率达到最大即为35.62 W，其最大效率达到85.44%，且当风速处于锁频即共振区间时，发电机具有良好的输出特性。

(3)通过分析确定了指数函数作为振幅函数的变量函数，且随着捕能柱摆动幅值的增大，发电机的输出功率和效率均增大，但当振幅倍数大于1时，发电机的效率增幅变缓。

上述所得结论可为应用于无叶片风力机的永磁直线发电机的设计提供指导。