空间集聚对制造业生产率的影响研究
——基于两位数行业数据的再估计
王 猛,习 敏
(陕西师范大学 国际商学院,陕西 西安 710119)
一、引言
改革开放以来,中国积极融入制造业全球价值链,得以建立起门类齐全的制造业体系。制造业的快速发展成为中国经济高速增长的引擎。如何提升制造业生产率一直是关乎中国经济高质量发展的重要问题,这一问题在经济结构性减速的新常态下更加突出。本文试图证明,继续推动制造业集聚以发掘空间红利,可能是提升中国制造业生产率的一个重要突破口。
理论上看,空间集聚会产生正的外部性,进而提升制造业生产率。这种正的外部性既包括专业劳动力市场、中间投入品共享、知识溢出等供给侧机制(Marshall,1920[1]),也包括本地市场效应等需求侧机制(Krugman,1991[2])。当然,随着空间集聚进一步加强,土地、劳动力等要素的价格上升可能造成负的外部性,从而降低制造业生产率(Krugman,1991[2])。西方发达国家的经验表明,空间集聚产生的正的外部性能显著提升制造业生产率(Cingano和Schivardi,2004[3];Otsuka和Yamano,2008[4];Antonietti和Cainelli,2011[5];Lee等,2013[6]),也有研究发现了负的外部性,即空间集聚会降低制造业生产率(Martínez等,2007[7];Broersma和Ooterhaven,2009[8];Rizov和Oskam,2012[9])。
那么,空间集聚如何影响中国的制造业生产率?现有研究的结论可归纳为“线性”和“非线性”两类。大部分研究发现,空间集聚产生的正的外部性能显著提升制造业生产率,即二者间存在正向的线性关系(柯善咨和姚德龙,2008[10];陈柳,2010[11];张公嵬和梁琦,2010[12];张公嵬等,2013[13];张先锋和胡翠群,2013[14];胡玫等,2015[15];韦曙林和欧梅,2017[16];张超和周立新,2018[17];曹正旭等,2020[18];杨浩昌等,2020[19])。但也有研究指出,由于正的外部性、负的外部性交替占据主导地位,空间集聚对制造业生产率的影响是非线性的:二者间可能存在倒U形或U形关系(袁骏毅、乐嘉锦,2018[20];陈阳和唐晓华,2019[21]);也可能导致空间集聚的作用随时间推移出现反转(孙浦阳等,2013[22];金春雨和程浩,2015[23])。
鉴于现有研究的众说纷纭,对此问题形成共识性结论需要进一步分析。本文将基于2001—2016年20个两位数行业面板数据,就空间集聚对制造业生产率的影响进行再估计。对全样本的固定效应估计证实了正向线性关系的存在,即空间集聚显著提升了制造业生产率。进一步的门限回归则发现空间集聚与制造业生产率之间存在一定的非线性关系:空间集聚的水平提高导致其对全要素生产率的影响增强,但对劳动生产率则缺乏类似影响。
此外,高生产率抑或低生产率的制造业更易受空间集聚的影响?空间集聚与制造业生产率的因果关系在不同要素密集度的行业间是否存在差异?上述问题目前仍缺乏充分的探讨,本文将尝试加以回答。采用分位数回归研究空间集聚对不同制造业生产率水平的差异化影响,发现空间集聚的影响随制造业生产率的提升而减弱。按照要素密集度对制造业分组进行分样本回归,考察空间集聚影响制造业生产率的行业异质性,结果表明空间集聚的影响主要体现在资本密集型、劳动密集型行业,在技术密集型行业不显著。
本文结构安排如下:第二部分报告模型、数据和变量,第三部分展示并分析回归结果,第四部分得出结论并讨论其政策含义。
二、研究设计
(一)模型设定
为估计空间集聚对制造业生产率的影响,本文构造以下回归模型:
mpit=β0+β1aggit+β2controlit+μi+ζt+εit
(1)
式(1)中,mp为制造业生产率,agg为空间集聚,control为影响制造业生产率的一系列控制变量,μ为行业固定效应,ζ为年份固定效应,ε为随机误差项,i和t分别表示制造业行业和年份,β0~β2为待估的参数向量。
(二)数据来源和变量选择
本文选取2001—2016年的制造业两位数行业为研究样本。数据来源包括国家统计局数据库以及历年《中国工业统计年鉴》《中国科技统计年鉴》。按现行统计制度,样本期内的行业划分依据1994年、2002年、2011年3个版本的《国民经济行业分类》进行,存在行业口径不一致的问题。对此,本文参考余泳泽等(2017)[24],将2011年版《国民经济行业分类》中的“汽车制造业”和“铁路、船舶、航空航天和其他设备制造业”合并为2002年版《国民经济行业分类》中的“交通运输设备制造业”。同时剔除2011年版《国民经济行业分类》新增的“皮革、毛皮、羽毛及其制品和制鞋业”“木材加工和木、竹、藤、棕、草制品业”“家具制造业”“印刷和记录复制业”“文教、工美、体育和娱乐用品制造业”和“橡胶和塑料制品业”等行业。最终研究个体确定为20个制造业两位数行业,得到320个观测值。考虑到制造业行业间存在较大的异质性,本文借鉴张其仔和李蕾(2017)[25]的做法,利用模糊聚类分析将20个两位数行业分为劳动密集型、资本密集型和技术密集型3类。①
1.被解释变量
对于被解释变量制造业生产率,本文选择劳动生产率(lp)、全要素生产率(tfp)两种指标加以测量。
劳动生产率是制造业的产出与劳动投入之比。制造业的产出指标包括增加值、总产值和销售产值等。限于数据可得性,本文参考唐晓华等(2017)[26],用规模以上工业企业的销售产值表示制造业产出,并根据工业品出厂价格指数(PPI)调整为2001年不变价。制造业的劳动投入指标用规模以上工业企业的从业人数表示,并对2012年的缺失值取均值补齐。
全要素生产率中涉及的制造业产出、劳动投入指标与劳动生产率相同。此外,全要素生产率计算还涉及资本存量的投入。借鉴余泳泽等(2017)[24],本文用永续盘存法(PIM)计算规模以上工业企业的资本存量,步骤如下:(1)使用2001年固定资产净值作为基期资本存量K0;(2)用第t年与t-1年的固定资产原价之差表示新增投资额It,并根据固定资产投资价格指数调整为2001年不变价;(3)用第t年与t-1年的累计折旧之差表示本年折旧Zt,进而用Zt除以第t-1年的固定资产原价,得到折旧率δt;(4)依据公式Kt=It+ (1-δt)Kt-1,计算2002年及以后各年的资本存量。最后,基于规模以上工业企业的产出、劳动投入、资本存量数据,用数据包络分析(DEA)计算可变规模报酬下的纯技术效率,作为制造业全要素生产率的度量。
2.核心解释变量
本文选择区位基尼系数(gini)衡量制造业空间集聚。作为基尼系数在区域和产业研究中的应用,区位基尼系数因其计算简单、对应的洛伦兹曲线直观而得到广泛使用(戴平生,2015)[27],其计算公式为:
(2)
式(2)中,gini为区位基尼系数,其取值范围为[0, 1]。yi和yj表示第i、j个省级行政区规模以上工业企业的从业人数占全国的份额(i,j=1,…,n),μ为各省级行政区的均值。空间基尼系数的值越接近于1,表明制造业的空间集聚水平越高。
3.控制变量
为缓解遗漏变量造成的内生性问题,本文引入以下控制变量:(1)劳均资本存量(k)。劳均资本存量是影响生产率的核心变量,用规模以上工业企业的资本存量和从业人数之比表示。(2)研发投入(r&d)。研发投入的大小与技术进步密切相关,进而影响生产率。用大中型工业企业新产品销售收入占主营业务收入的比重表示。(3)国有产权比重(soe)。国有产权比重越高,意味着该行业的市场化程度较低,从制度视角看可能不利于生产率提升。用国有企业的主营业务收入与规模以上工业企业主营业务收入之比表示。(4)对外开放(open)。对外开放为制造业提供了参与国际市场竞争的机会,有利于企业学习和创新,从而提升生产率。用规模以上工业企业的出口交货值与销售产值之比表示。
(三)描述性统计
制造业生产率在两位数行业间存在较大的差异。从劳动生产率看,烟草制品业和石油加工、炼焦及核燃料加工业最高,2001—2016年的平均劳动生产率分别高达249.59和130.05;纺织业和纺织服装、鞋、帽制造业处于最低水平,平均劳动生产率分别为25.18和36.64。从全要素生产率看,烟草制品业和通信设备、计算机及其他电子设备制造业的生产率最高,2001—2016年平均全要素生产率均为1;非金属矿物制品业、造纸及纸制品业的平均全要素生产率最低,分别仅有0.42和0.41。
总体上,20个两位数行业在2001—2016年的平均集聚水平为0.56。其中,通信、计算机及其他电子设备制造业,纺织服装、鞋、帽制造业的平均集聚水平最高,分别达到0.76和0.73;医药制造业、有色金属冶炼及压延加工业的平均集聚水平最低,分别为0.43、0.42。
主要变量的描述性统计见表1。为减轻异方差问题,对劳动生产率和劳均资本存量作对数化处理。
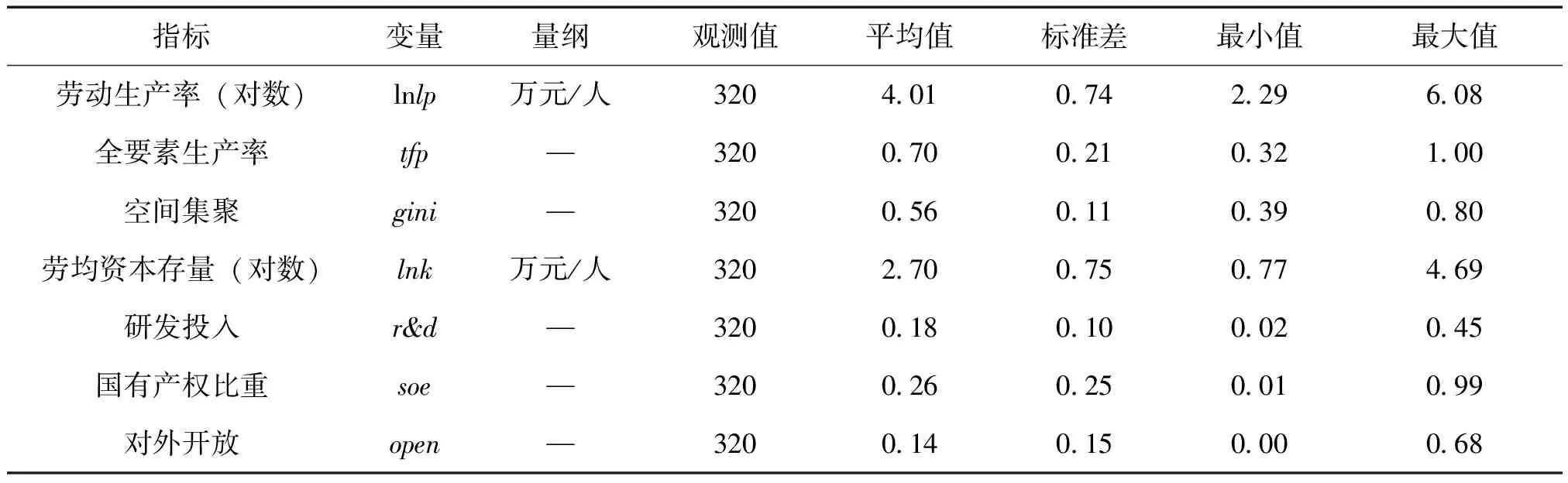
表1 主要变量的描述性统计
三、回归结果及分析
(一)全样本回归
参数估计前,对回归模型进行Hausman检验,检验值为19.05,对应的p值为0.0041,表明应选择固定效应估计。全样本回归结果见表2,其中模型1~3以劳动生产率为被解释变量,模型4~6以全要素生产率为被解释变量。
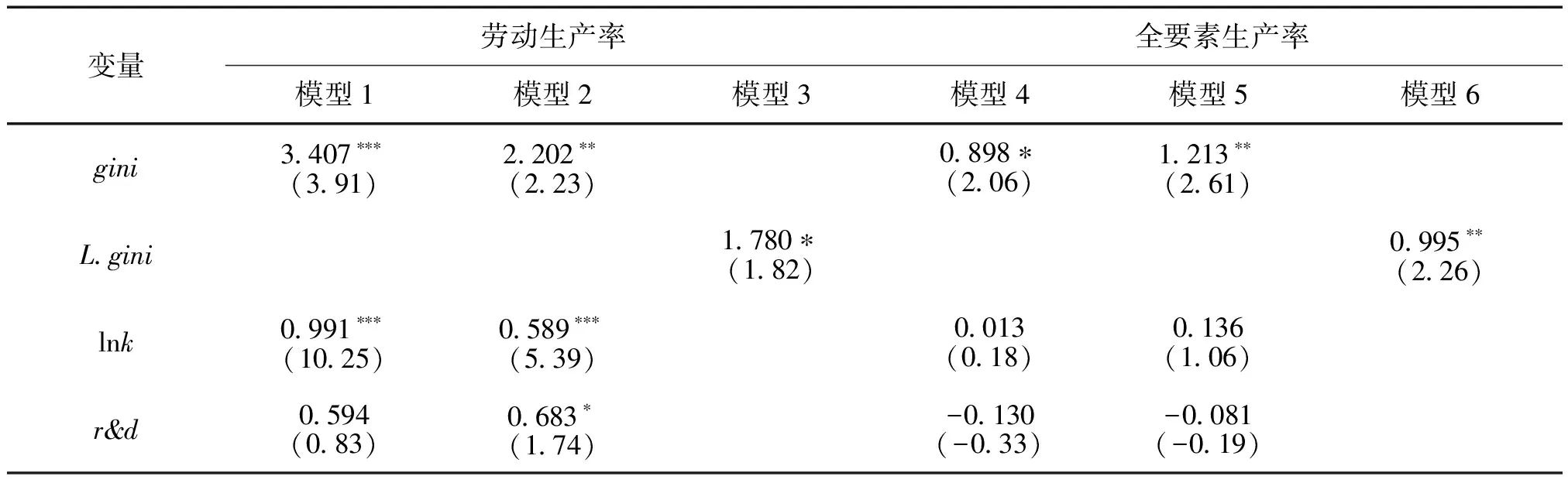
表2 空间集聚与制造业生产率:全样本回归
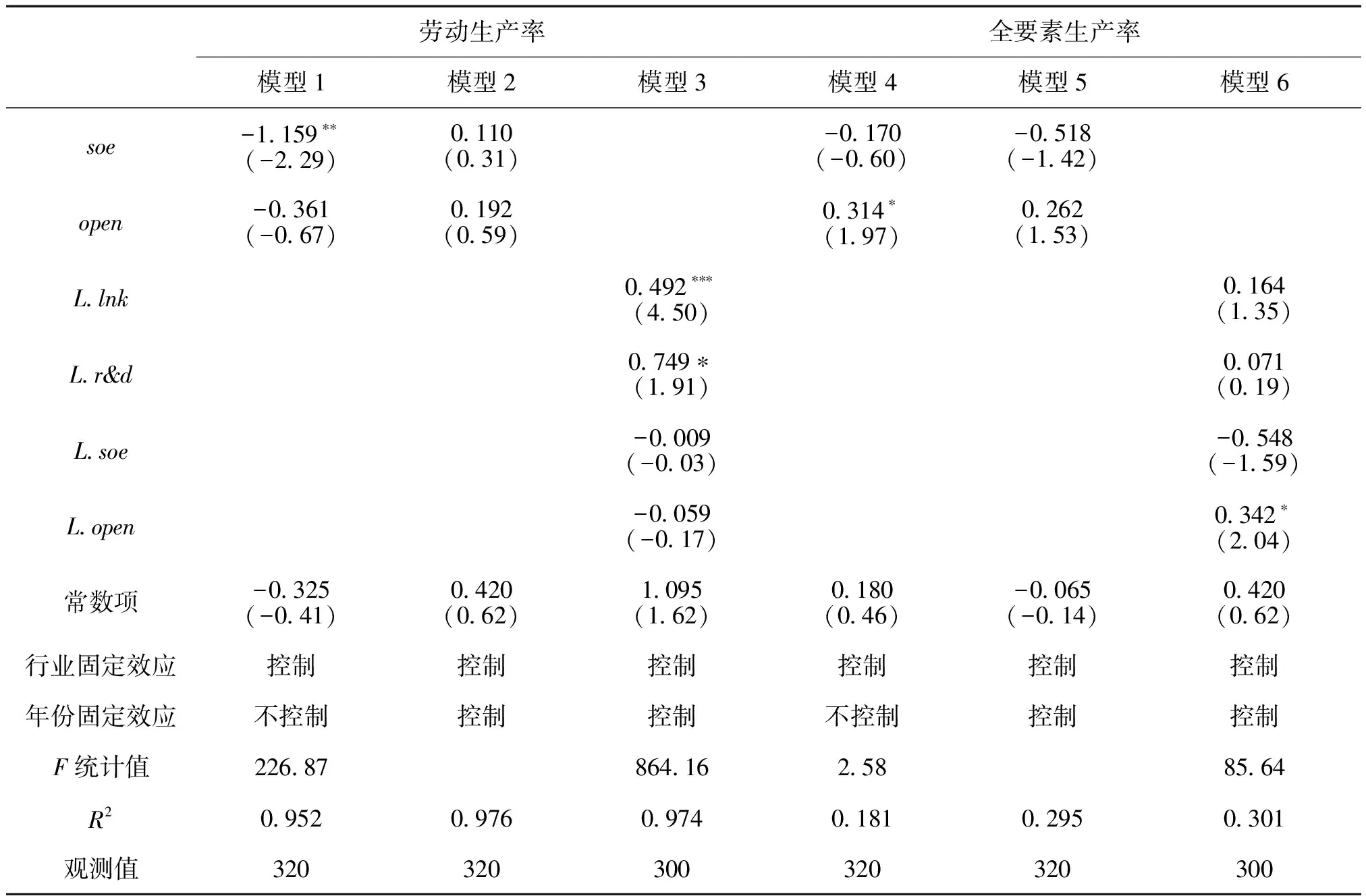
续表
在模型1、模型4未控制年份固定效应时,区位基尼系数的系数估计值为正,且分别通过1%和10%水平的显著性检验;模型2、模型5同时控制行业和年份固定效应后,区位基尼系数的系数估计值仍在5%水平上显著为正。这说明空间集聚对制造业生产率具有促进作用,即二者间存在正向的线性关系。专业劳动力市场、中间投入品共享、知识溢出和本地市场效应等构成了正的外部性(Marshall,1920[1];Krugman,1991[2]),有助于提升制造业生产率。
有必要讨论联立内生性问题。空间集聚固然显著促进了制造业生产率,但为了追求较高的制造业生产率水平,制造业布局也可能发生相应调整,因此制造业生产率会反过来影响空间集聚。为缓解这种反向因果导致的内生性问题,模型3、模型6对所有解释变量均滞后一期。核心解释变量的估计系数仍然为正,且分别通过10%和5%水平的显著性检验。可见,考虑联立内生性后,空间集聚对制造业生产率的正向影响具有稳健性。
控制变量中,劳均资本存量、研发投入显著提高了劳动生产率,但不能提高全要素生产率,国有产权比重和对外开放的作用则不显著。
(二)门限回归
全样本回归结果证实了空间集聚具有正的外部性,且与制造业生产率之间存在正向的线性关系。但现有文献指出,由于正的外部性、负的外部性交替占据主导地位,空间集聚对制造业生产率的影响也可能是非线性的。这一类文献通常在回归模型中加入空间集聚的二次项。在样本量较小时,这种做法往往导致较严重的多重共线性问题,影响参数估计的有效性。基于这一考虑,本文采用门限回归检验空间集聚与制造业生产率的非线性关系。这一处理能有效避免多重共线性对参数估计结果的干扰,增强结论的可信度。
以核心解释变量作为门限变量,依次估计单门限效应和双门限效应,结果如表3所示。以劳动生产率为被解释变量时,单门限值、双门限值均未通过显著性检验,可见空间集聚与制造业劳动生产率之间并不存在非线性关系。
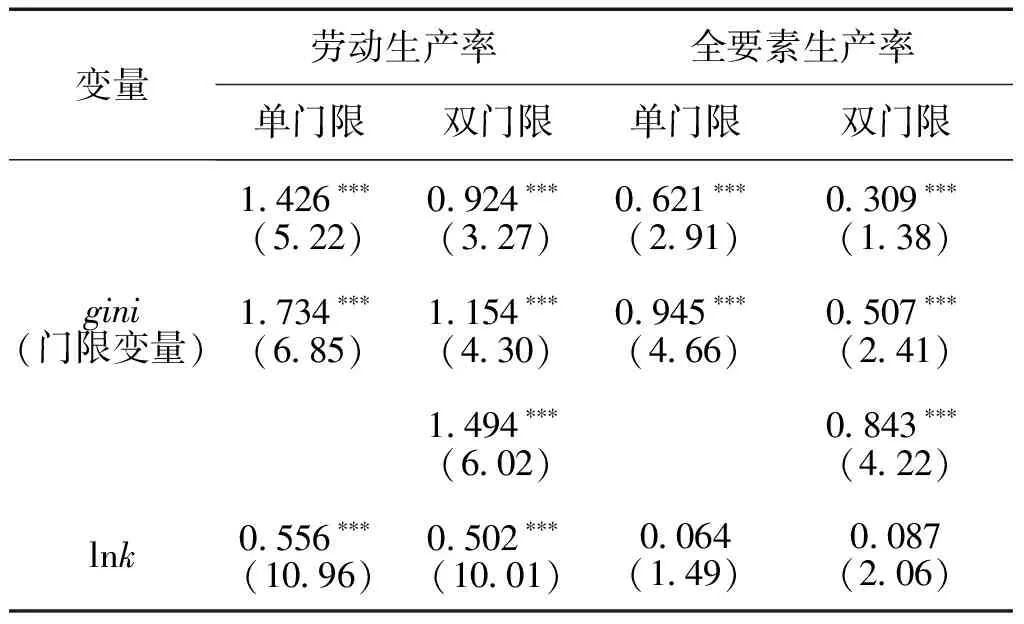
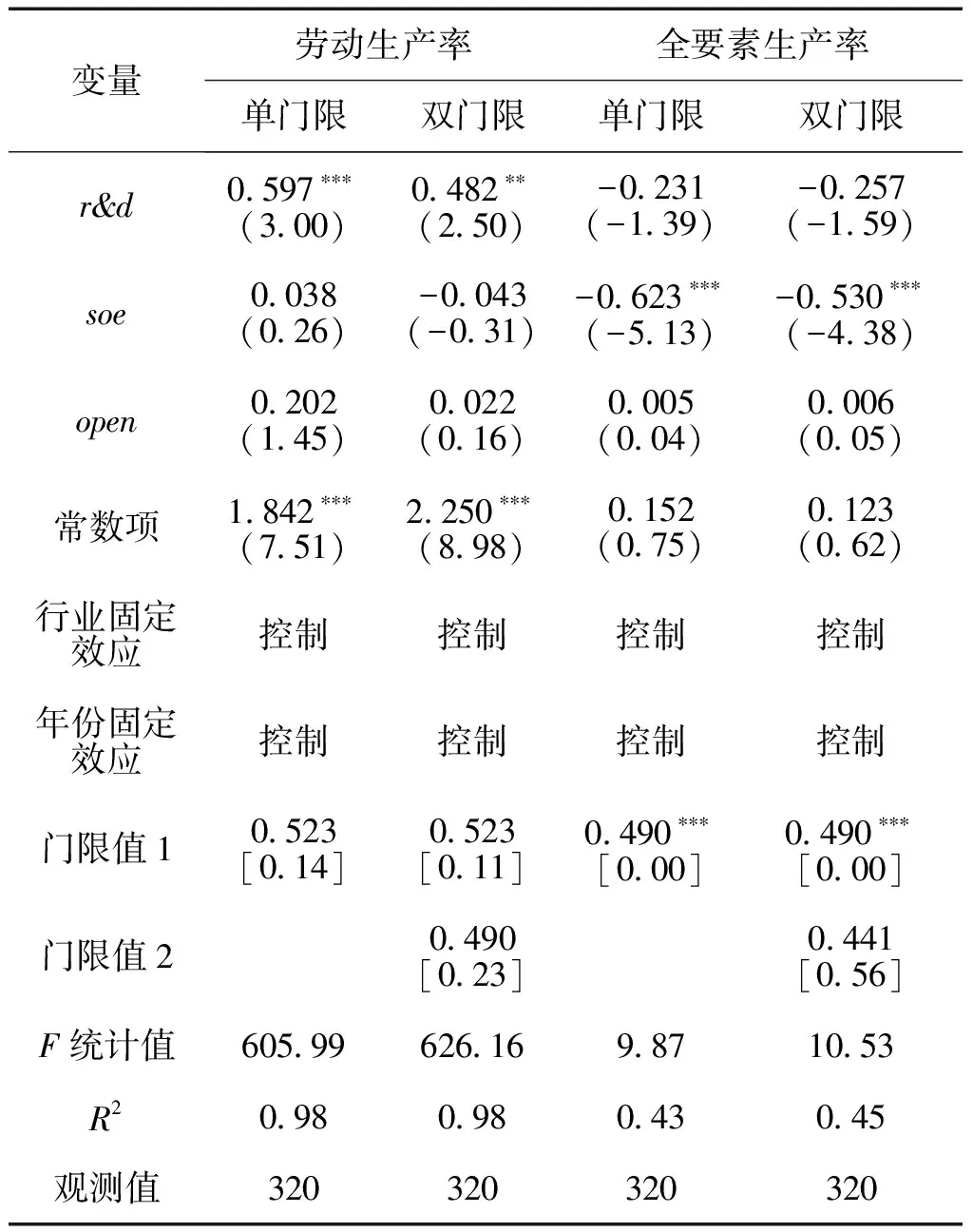
表3 空间集聚与制造业生产率:门限回归
续表
但以全要素生产率为被解释变量时,空间集聚的门限值1通过了1%水平的显著性检验,门限值2则未通过显著性检验,可见空间集聚具有单门限效应,门限值为0.49。在[0, 0.49)区间,空间集聚的估计系数为0.62;在[0.49, 1]区间,空间集聚的估计系数增大至0.95。这就意味着空间集聚与制造业全要素生产率之间存在非线性关系。空间集聚水平提高会更加促进全要素生产率提升。需要说明的是,单门限两边的估计系数均为正数,而非“一正一负”,说明这种非线性关系并不是U形或者倒U形。
门限回归进一步验证了全样本回归的结果,即空间集聚发挥了正的外部性,且没有产生负的外部性。
(三)分位数回归
接下来,本文将基于分位数回归,讨论空间集聚对不同水平的制造业生产率的影响是否存在差异。将面板数据和分位数回归相结合,不仅可以测度解释变量对被解释变量的某个特定分位点的边际效果,还可控制个体差异以避免极端值对结果的干扰,使得回归结果更加精确和稳定。参照任思雨等(2019)[28],本文分别以劳动生产率、全要素生产率作为被解释变量,在0.1、0.25、0.5、0.75和0.9分位点上进行参数估计,其结果见表4。限于篇幅,仅报告空间集聚变量的估计系数。
表4中,以劳动生产率为被解释变量时,空间集聚的系数估计值在0.1分位点为2.229,在0.25、0.5分位点下降至2.219和2.203,在0.75、0.9分位点则进一步下降至2.185和2.173,且均通过了显著性检验。以全要素生产率为被解释变量时,系数估计值的变动趋势相同:在0.1分位点为1.337,在0.25、0.5分位点下降至1.296和1.219,在0.75、0.9分位点则进一步下降至1.131和1.090。

表4 空间集聚与制造业生产率:分位数回归
核心解释变量的系数随分位点的上升而下降,表明空间集聚对制造业生产率的影响与制造业生产率本身的水平密切相关。制造业生产率较低时,受空间集聚的影响更为强烈。随着制造业生产率的提高,空间集聚的影响也逐渐减弱。这一发现意味着,与生产率较高的制造业行业相比,那些生产率水平低下的制造业行业从空间集聚中获益更大。
(四)分样本回归
全样本回归证实了空间集聚对制造业生产率有正向影响。这种影响在不同要素密集度的行业间是否存在差异?为回答这一问题,本文对劳动密集型、资本密集型和技术密集型行业样本分别进行回归,结果见表5。
表5中,以劳动生产率为被解释变量时,空间集聚的系数估计值在资本密集型行业中为6.215,且通过了1%水平的显著性检验,在劳动密集型和技术密集型行业中不显著。以全要素生产率为被解释变量时,空间集聚的系数估计值在资本密集型行业中为3.573,且通过1%水平的显著性检验,在劳动密集型行业中为1.483,且在10%水平上显著,在技术密集型行业中不显著。这一结果表明,空间集聚对生产率的促进作用主要存在于资本密集型、劳动密集型行业。限于数据可得性,本文无法进一步考察其中的作用机制,有待后续研究的补充。

表5 空间集聚与制造业生产率:分样本回归
四、结论与政策含义
对中国这样的制造业大国而言,提升制造业生产率关乎中国经济的高质量发展。本文从空间集聚的视角探讨制造业生产率的提升路径。针对现有文献的不足,本文基于2001—2016年20个两位数行业的面板数据,对空间集聚对制造业生产率的影响进行再估计,结论如下:第一,全样本回归中控制了劳均资本存量、研发投入、国有产权比重和对外开放等变量后,空间集聚显著提升了制造业生产率,证实二者间整体上存在正向的线性关系。第二,根据门限回归结果,空间集聚与制造业生产率存在一定的非线性关系。空间集聚水平的提高会强化其对全要素生产率的影响,但对劳动生产率则缺乏类似影响。第三,分位数回归表明,空间集聚对低生产率制造业的影响强于高生产率制造业,即空间集聚的作用强度与制造业生产率水平关系密切。第四,分样本回归结果显示,空间集聚对制造业生产率的影响主要体现在资本密集型、劳动密集型行业,在技术密集型行业并不显著。
上述结论为从空间集聚角度提升中国的制造业生产率提供了政策启示。本文证明空间集聚通过正的外部性提升了制造业生产率,且并未发现空间集聚会产生负的外部性,这意味着政策上应坚持推动制造业的空间集聚,以充分发挥其正的外部性。具体地,应从以下三个方面着手。首先,鉴于制造业生产率较低时受空间集聚的影响更为强烈,那些生产率水平低下的制造业行业从空间集聚中获益更大,应特别鼓励纺织业,纺织服装、鞋、帽制造业,造纸及纸制品业等低生产率行业的空间集聚。其次,由于空间集聚对中国制造业生产率提升的影响主要存在于具备比较优势的劳动密集型行业,以及可能建立竞争优势的资本密集型行业,因此应着重推动这些行业的空间集聚。最后,构建促进要素自由流动的制度环境。消除地方保护主义,打破区域间壁垒,是促进中国制造业集聚的根本举措。为此,应通过完善考核机制来弱化地方政府间的过度竞争,以消除制造业要素流动的体制性障碍,实现全国范围内的资源优化。
注释:
①120个两位数行业中,8个劳动密集型行业为:农副食品加工业,食品制造业,饮料制造业,纺织业,纺织服装、鞋、帽制造业,造纸及纸制品业,非金属矿物制品业,金属制品业;5个资本密集型行业为:烟草制品业,石油加工、炼焦及核燃料加工业,化学原料及化学制品制造业,黑色金属冶炼及压延加工业,有色金属冶炼及压延加工业;7个技术密集型行业为:医药制造业,通用设备制造业,专用设备制造业,交通运输设备制造业,电气机械及器材制造业,通信、计算机及其他电子设备制造业,仪器仪表及文化、办公用机械制造业。

