降雨条件下多级残积土坡渗流稳定性研究

黄剑斌，许旭堂，徐 祥，鲜振兴，刘道奇

(福建农林大学 交通与土木工程学院， 福建 福州 350108)

滑坡是一种极易造成重大人员伤亡和经济损失的自然灾害，其中降雨是滑坡发生的重要因素[1-5]。福建地区地处东南沿海，雨量充沛，雨季主要集中在3月—9月，梅雨和台风季节的降雨具有持续时间长、降雨强度大的特点。福建山区多级残积土边坡多，残积土的结构性强，具有浸水易崩解和软化、亲水性好等工程特性，每年因残积土坡失稳破坏造成的损失约占整个自然灾害的三分之一，严重制约着全省的经济发展。因此，开展降雨入渗对多级残积土坡渗流稳定性影响的研究，对此类边坡灾害防治与减灾研究具有重要的科学意义和现实意义。

目前对降雨条件下边坡的渗流特征和稳定性分析，已有不少研究。有些学者(何忠明等[6]、韩同春等[7]、蒋水华等[8])从计算方法入手，建立考虑渗流作用下边坡稳定分析模型，为准确计算降雨型边坡稳定性提供参考。张硕等[9]、许旭堂等[10-11]通过室内模型试验，分析降雨过程中坡体内部基质吸力、含水率、孔隙水压力及湿润峰等动态响应规律，探讨坡体裂缝发育及变形破坏模式。叶帅华等[12]以非饱和渗流理论为基础，通过建立三维模型，得出降雨条件下多级黄土高边坡基质吸力、有效应力和安全系数的变化规律。郭涛等[13]研究降雨入渗引起的土体抗剪强度劣化对残积土边坡稳定性的影响，指出采用抗滑桩加固可有效阻止土体下滑,但高饱和度条件下,应注意桩前土体的滑动引起边坡失稳。周伟杰等[14]通过建立有限元模型模拟边坡在不同降雨条件下东岭信滑坡的渗流特性及稳定性情况，得出不同降雨条件下边坡在雨中和雨后安全稳定性的变化规律。

虽然目前对降雨条件下边坡的渗流特征和稳定性研究取得很大进展，但以分析单级边坡为主，并多数立足于非饱和土力学的理论研究，而基于降雨充沛、气象复杂的福建地区，开展降雨入渗对多级残积土坡渗流稳定性影响的研究较少。因此，以顺邵高速多级边坡为例，结合饱和-非饱和渗流理论，基于现场实测数据，建立准确的流-固耦合模型，研究多级残积土坡在短时大雨和长时小雨两种工况下的渗流特征、应变特征及安全系数演化规律，并探讨不同工况下的边坡失稳预警方法，以期为降雨型多级残积土坡失稳预测和治理提供参考。

1 边坡概况及位移监测结果

1.1 工程概况

研究区位于福建省西北部山区顺邵高速公路A2标K14+260—K14+470左侧，高速公路沿线高陡边坡较多，受亚热带季风气候区影响，降雨期间常伴有边坡滑塌产生，局部甚至演变成大型滑坡地质灾害。边坡剖面图见图1，该边坡坡高34 m，分为4级，第一、二、三级各高8 m，第四级高10 m，坡度为30°，上部土层为厚度20 m～37 m的残积砂质黏性土；下部土层为厚度4 m～15 m的全风化云母石英片岩，各土层的物理力学性质由室内土工试验成果确定，详见表1。

表1 岩土体物理力学参数

图1 边坡剖面图

1.2 边坡变形监测方案

本次边坡变形监测时间为2018年5月5日—2018年6月30日，期间共采集7期数据(见表2)。测斜仪布置于第一、二、三阶平台中间位置，监测点编号依次为：ZK2、ZK1、ZK3(见图1)，沿着3个监测点的垂直深度方向每隔0.5 m读取深部水平位移数据；同时，用全站仪测量ZK1、ZK2两个布置点的地表沉降位移。

1.3 数据采集结果分析

以ZK1为例对数据采集结果进行分析，其中ZK1竖直向下0 m、2 m、4 m、6 m位置分别为点ZK11、点ZK12、点ZK13、点ZK14(见图1)。图2为监测点位移量和降雨量的时变曲线，图2(a)表明：位移变形曲线和累计降雨量曲线变化趋势一致，两者呈正相关关系。前3期每期累计降雨量较小，边坡水平位移增量变化不明显(见图2(b))；第5—第7期监测期间，累计降雨量大幅增加，位移增量显著增加。第4期—第5期监测期间，降雨量增加128 mm，监测期间ZK1监测孔自上到下水平位移增量分别为9.19 mm、8.56 mm、5.23 mm、3.69 mm；第5期—第6期监测期间，降雨量增加337 mm时，位移增量依次为26.48 mm、20.35 mm、14.21 mm、9.21 mm，位移增量幅度明显，且深度越浅、位移增量越大。总体上看，随着降雨量的增加，坡体位移增大；降雨增量越大，变形增量也越大(见图2(b))。

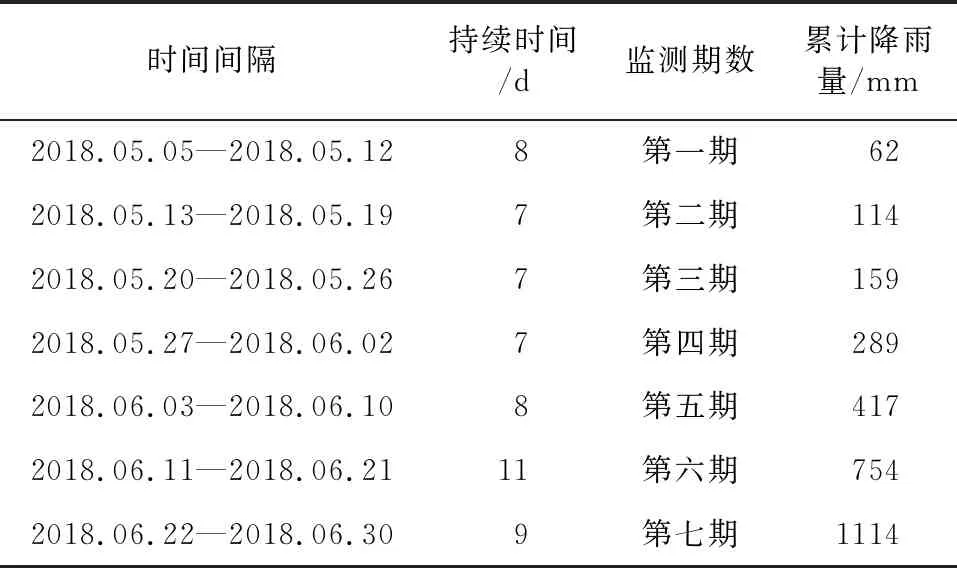
表2 边坡变形监测数据采集周期

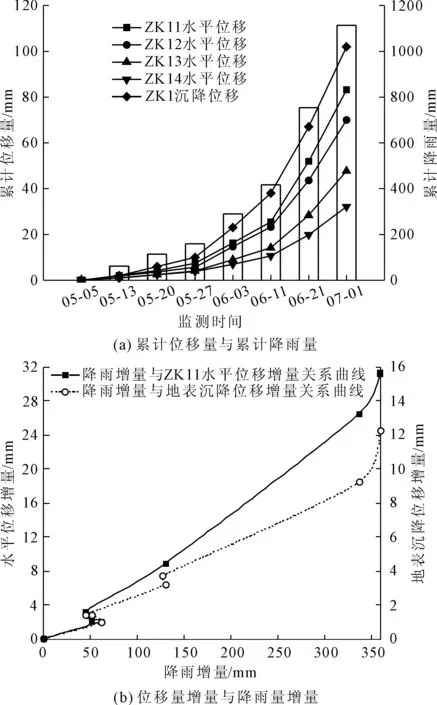
图2 位移量和降雨量的时变曲线

2 耦合模型

为分析长时小雨和短时大雨两种降雨工况下顺邵高速边坡的渗透变形和破坏机制，通过GeoStudio开展降雨-应力耦合分析，建立非稳态非饱和渗流耦合变形及稳定性计算模型，揭示不同工况下边坡渗流、应力应变及稳定性系数的动态演变过程。数值分析不考虑地震荷载，并以第七期实际累计降雨量(360 mm)作参考。依据气象部门对降水等级的划分，将最后一期日累计降雨量(见图3)转化为简化雨强和持时，工况1为长时小雨：降雨历时240 h，降雨强度1.5 mm/h；工况2为短时大雨：降雨历时36 h，降雨强度10 mm/h。同时，为了验证所建数值模型的准确性，将第一到第六期实际累计降雨量简化为对应的降雨历时和降雨强度(见图3)，随后把简化后的雨强和持时作为入渗强度施加于边坡坡面，以此进行降雨-应力耦合分析，并结合实测的位移数据进行验证。

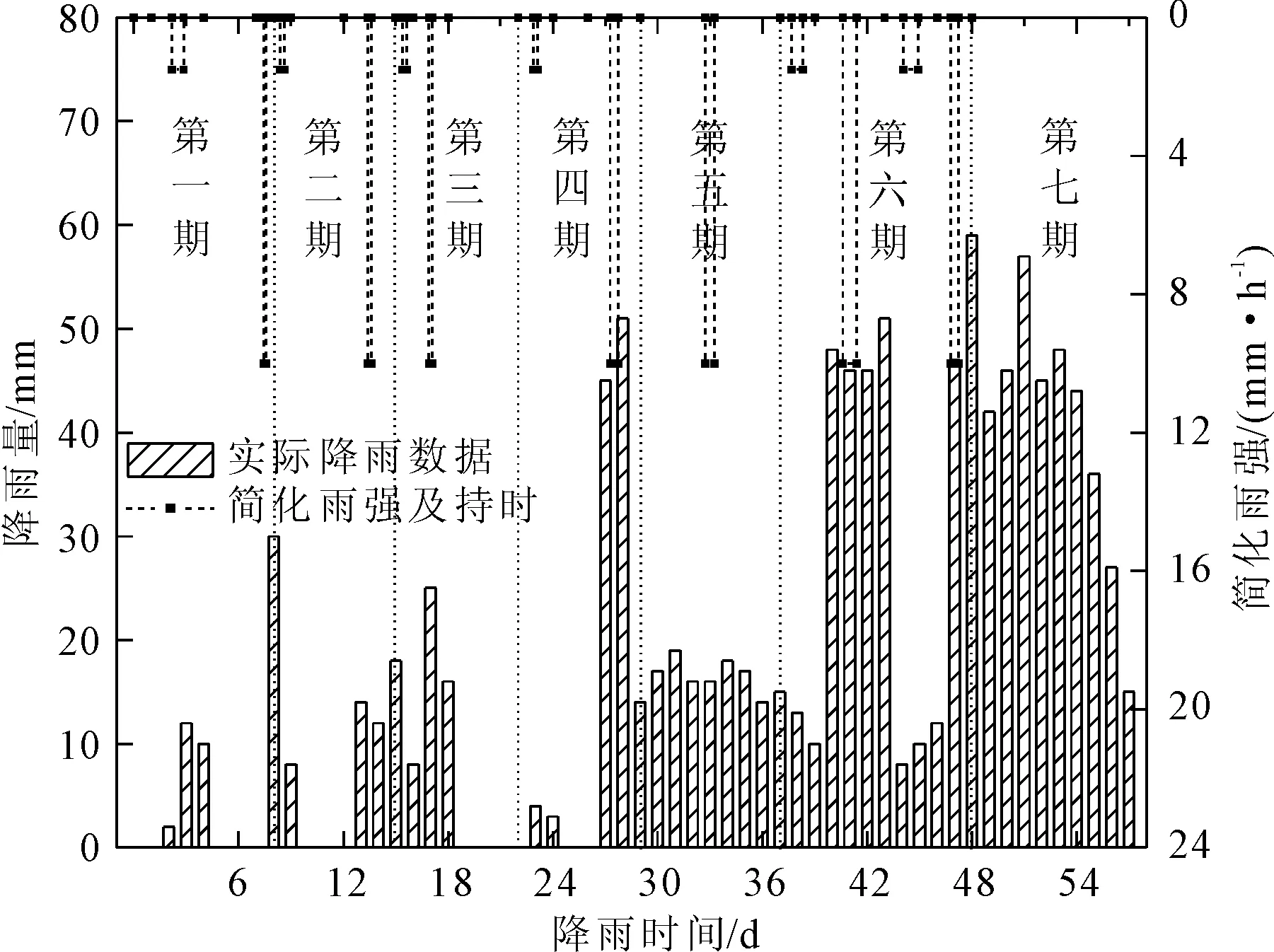
图3 每日降雨数据及简化雨强

2.1 边界条件及数值计算参数

流-固耦合模型边界条件包括两部分，一是降雨入渗边界，二是两侧的水平约束条件和底边的双向约束。模型两侧饱和区(边坡地下水位线位于土层的分界面)作为水头边界条件，模型两侧非饱和区为零流量边界，模型底部为不透水边界；长时小雨过程中，可能在坡表处形成暂态饱和区，即：地下水渗流可能沿着坡表溢出，因此坡表可定为渗流面。本构模型为理想弹塑性模型，采用三角形和四边形网格进行划分，宽度为2 m，共1 110个节点，1 050个单元(见图1)。渗流分析所需的土水特征曲线SWCC和渗透系数函数HCF由室内试验成果及参考类似工程[15～17]综合确定(见图4、图5)。

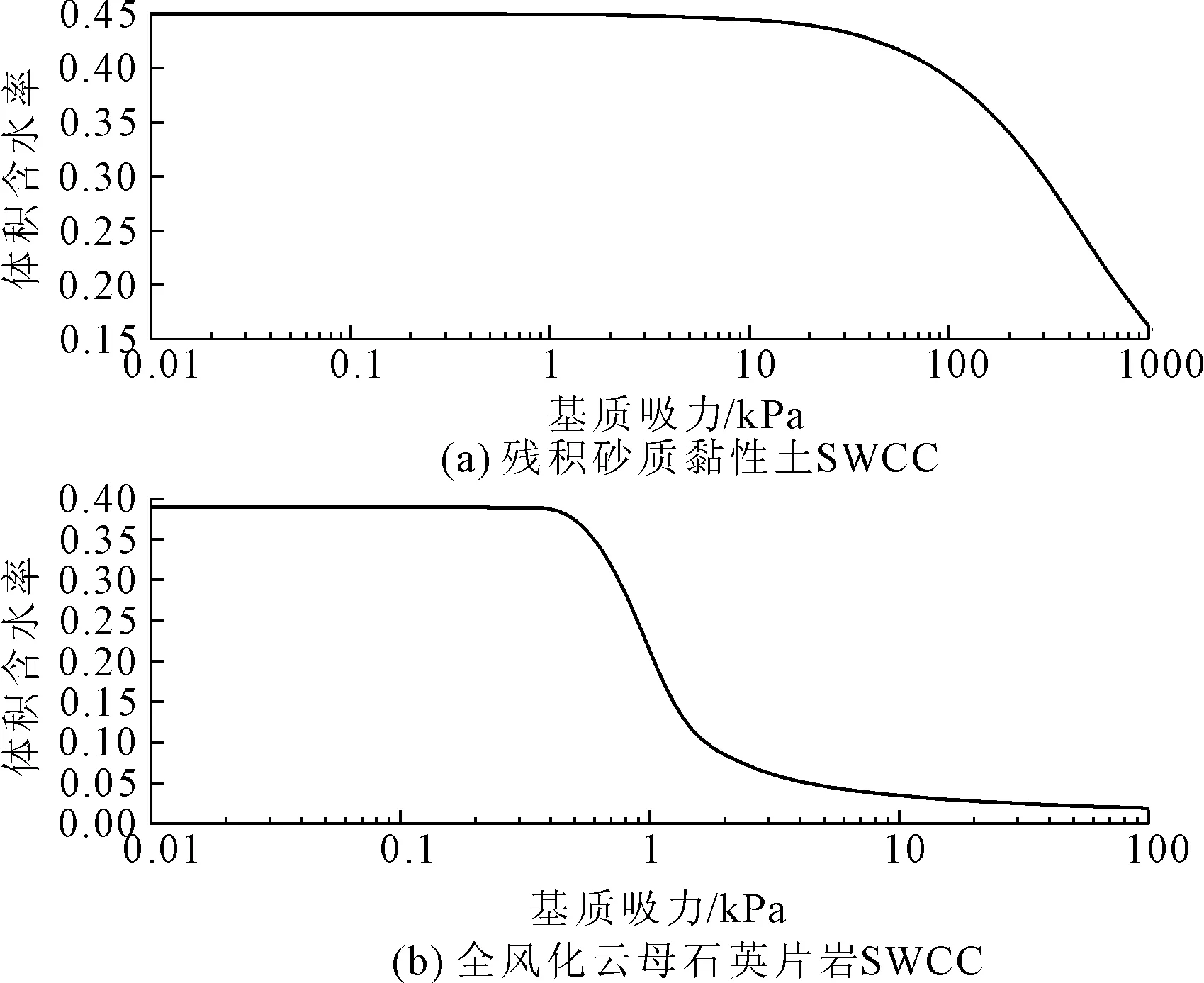
图4 各土层土水特征曲线

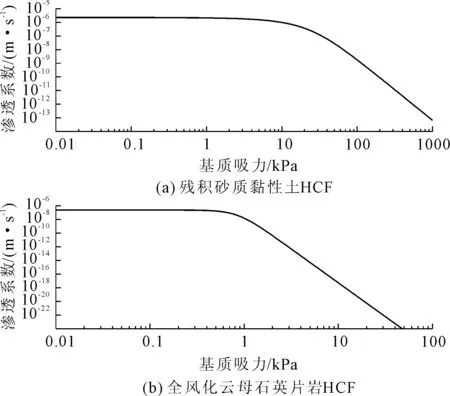
图5 各土层渗透系数函数

2.2 模型准确性评价

将ZK11、ZK12、ZK13、ZK14的累计水平位移数值计算值与实测值以及ZK1、ZK2的沉降位移计算值与实测值进行比较，并对模型计算值与实测值的相关性进行分析，以此评价数值模型的准确性。图6为各期实测累计水平/沉降位移与模型计算值的比较，ZK11、ZK12、ZK13、ZK14的累计水平位移计算值与实测值的平均相对误差依次为：8%、5%、11%、12%，ZK1、ZK2的沉降位移计算值与实测值的平均相对误差分别为：8%、11%，模型计算值与实测值相关系数为0.997 3(见图7)，以上表明：所建数值模型能较好的反映降雨条件下边坡渗透、变形和稳定性的变化。

3 数值分析结果

3.1 渗流分析

图8为监测点ZK11、ZK12、ZK13、ZK14在天然状态、短时大雨和长时小雨工况下边坡孔隙水压力随时间的变化图。天然状态下(见图8(a))，边坡监测点孔隙水压力随时间推移有小幅度变化，变化幅度与土层深度呈反比，边坡孔隙水压力沿着高程有规律分布(见图9(a))。短时大雨工况下(见图8(b))，随着降雨的进行，边坡孔隙水压力迅速增长，坡表ZK11点仅在降雨12 h时增至最大，坡体出现暂态饱和区，暂态饱和区的范围会随着降雨的进行而增加(见图9(b))。因雨水入渗至深处需要一段时间，所以随着深度的增加，孔隙水压力的变化呈现出三阶段：初始增长缓慢阶段、近似线性快速增长阶段、缓慢增长阶段，深部孔压增长至最大值的时间也越长，整个降雨过程中，浅层的孔隙水压力增长速度远大于坡体内部。长时小雨工况下(见图8(c))，坡体孔隙水压力变化趋势与短时大雨工况下基本一致，孔压增长速度整体上看较为缓慢，但是影响范围更大，深部孔隙水压力也发生显著变化(见图9(c))。同一深度下，暂态饱和区变化幅度比短时大雨工况下更小(见图9(b))。坡表ZK11点经历80 h小雨后才增至最大值，孔压的最大值也较小。综上分析，降雨强度越大，孔隙水压力整体增长速度较快，其变化速度与降雨强度的大小存在一定的相关性。

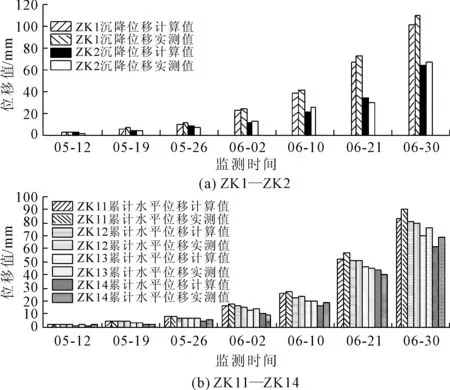
图6 实测累计水平/沉降位移与模型计算的比较

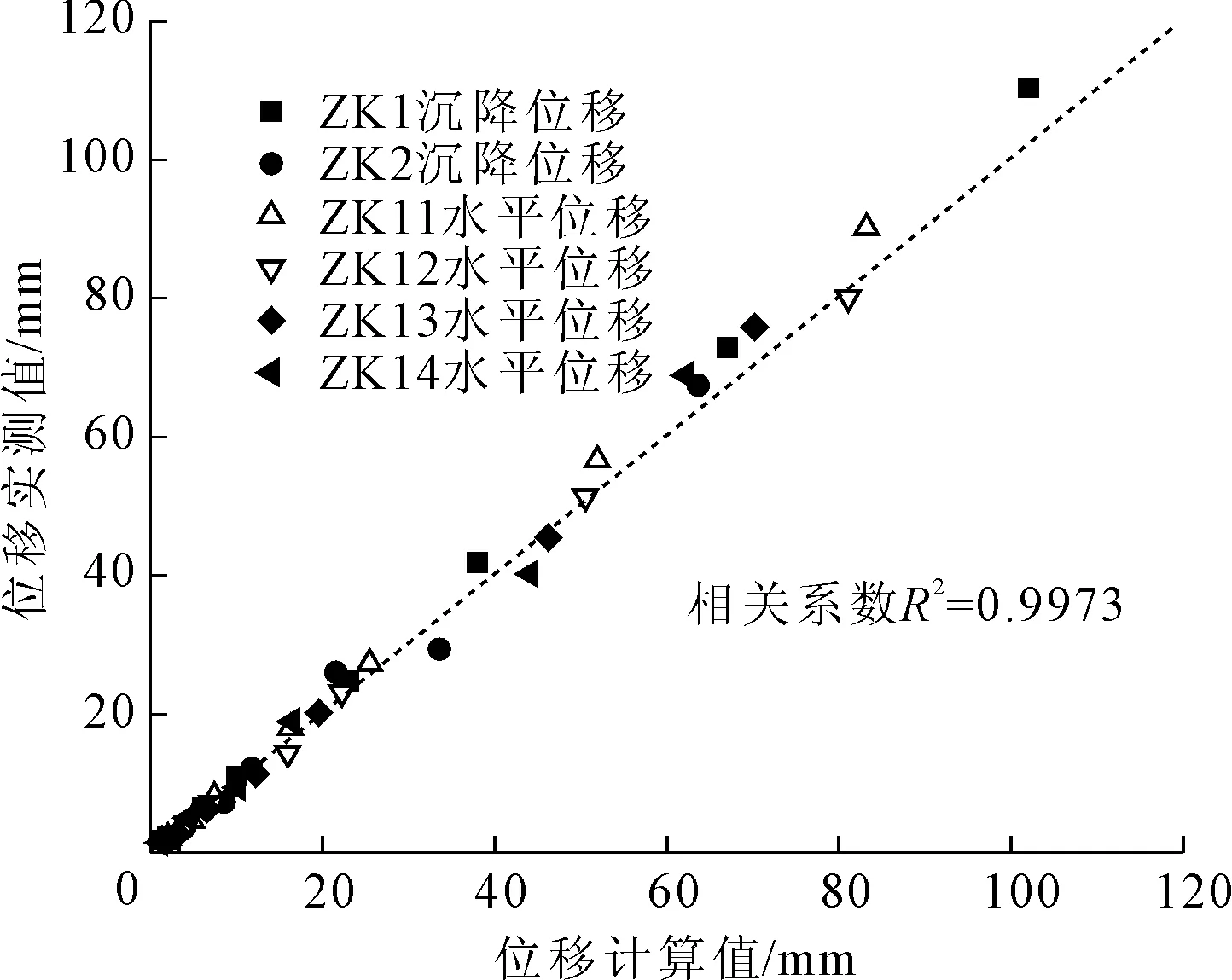
图7 位移计算值与实测值的相关性分析

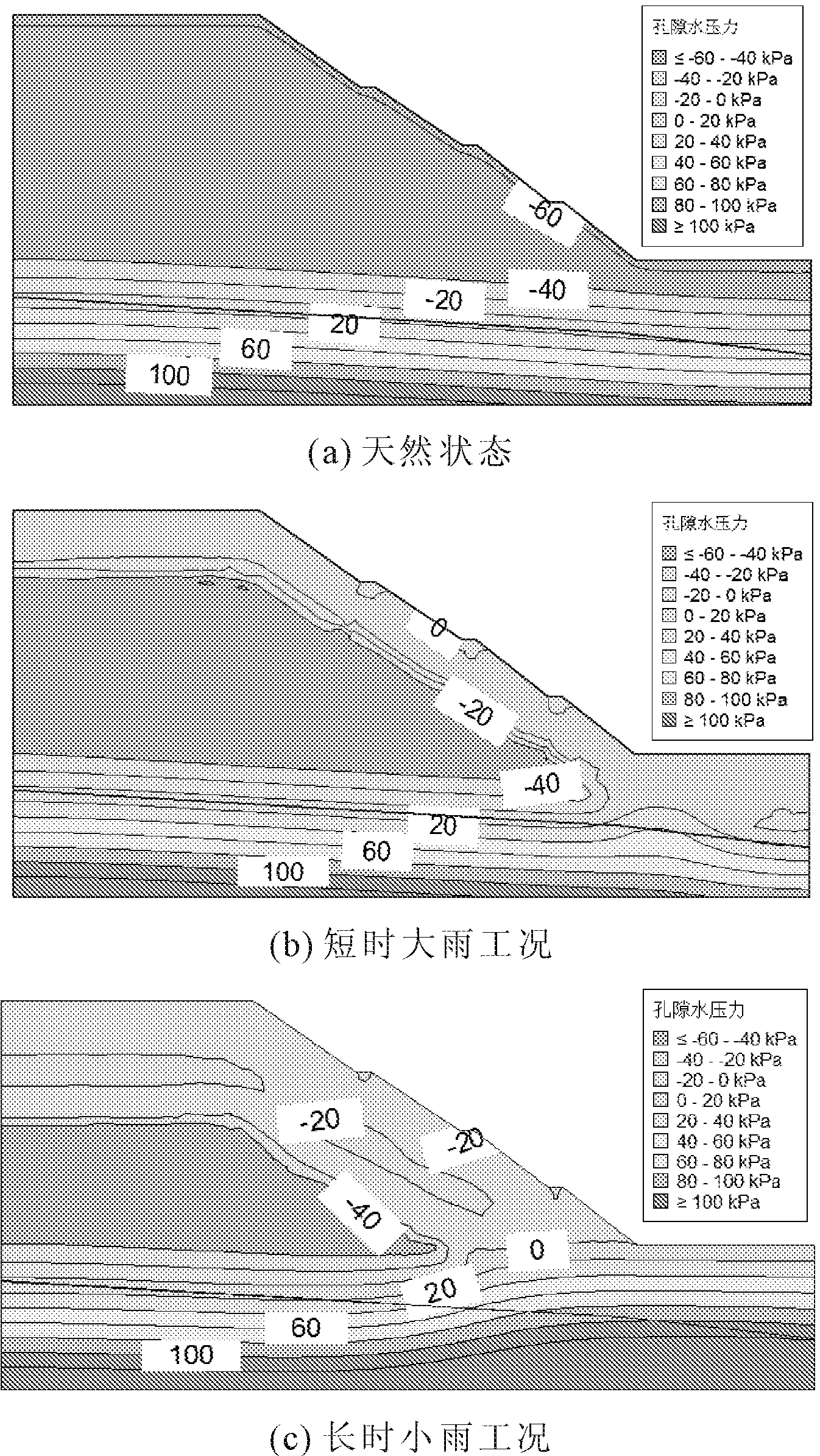
图9 不同降雨工况下孔隙水压力沿坡体分布图

长时小雨下，雨水以垂直入渗为主，持续入渗的效果显著，随着雨水入渗至坡体深处，地下水位可持续上升(上升幅度明显)，饱和区域逐渐向上扩张；短时大雨下，部分雨水以坡面径流为主，入渗效果不佳。以上不同降雨条件下的孔压分布表明：若以孔压为预警因子选择，长时小雨应以深部孔压变化为宜，而短时大雨应以浅部孔压变化为准。

3.2 应变分析

短时大雨工况下边坡X方向(见图10(a))应变集中在坡脚和坡面，坡脚应变由正值向坡体内逐渐过渡到0，即边坡在X方向应变为压缩状态，随着深度加深，压缩量越小。Y(见图10(b))方向应变等值线与坡面基本平行，覆盖坡顶、坡底和坡面，且较为密集，形成应变集中，并与坡面基本平行。与天然状态相比，短时大雨工况下X方向和Y方向应变显著增大，等值线分布更为密集，应变集中现象更显著，边坡有浅层向下滑动趋势。

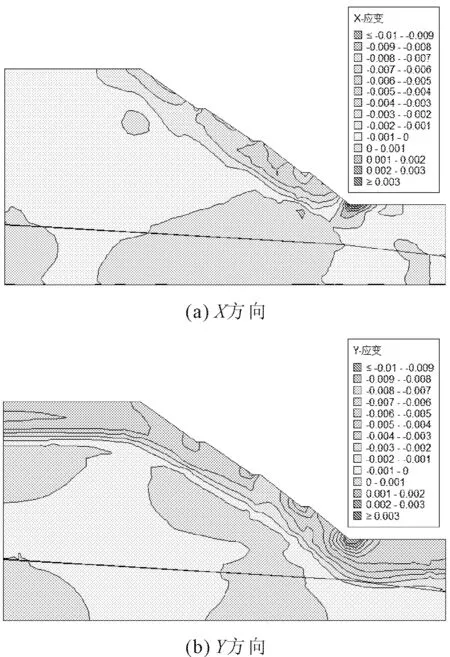
图10 短时大雨工况不同方向上应变等值线图

长时小雨工况下边坡X方向(见图11(a))应变集中在坡脚，相比短时大雨工况，应变集中在坡脚的范围更大，且与短时大雨工况一样，由正值向坡体内逐渐过渡到0。Y方向(见图11(b))应变等值线更为密集，也覆盖到坡顶、坡底和坡面，但不规则，与短时大雨工况相比，长时小雨对边坡造成的应变影响深度更深，影响范围更大，所以可能会引发深层滑坡的发生。基于不同降雨条件下边坡坡体的应变发展，在降雨诱发多级残积土坡的失稳过程中应注重坡脚防护，以降低边坡坡脚局部坍塌引发的渐进累积破坏。

3.3 边坡安全系数变化分析

天然工况下，边坡经历240 h的安全系数为1.455(见图12(a))；短时大雨下，边坡安全系数急剧下降到1.296(见图12(b))，最危险滑移面位于浅层上级坡面圆弧形滑坡；长时小雨下，边坡安全系数下降到1.214(见图12(c))，与短时大雨工况相比，最危险滑移面深度更深，范围更大，覆盖整个坡面。即：同一累计降雨量下，长时小雨对边坡稳定性造成的影响更大，可能以深部滑坡为主。

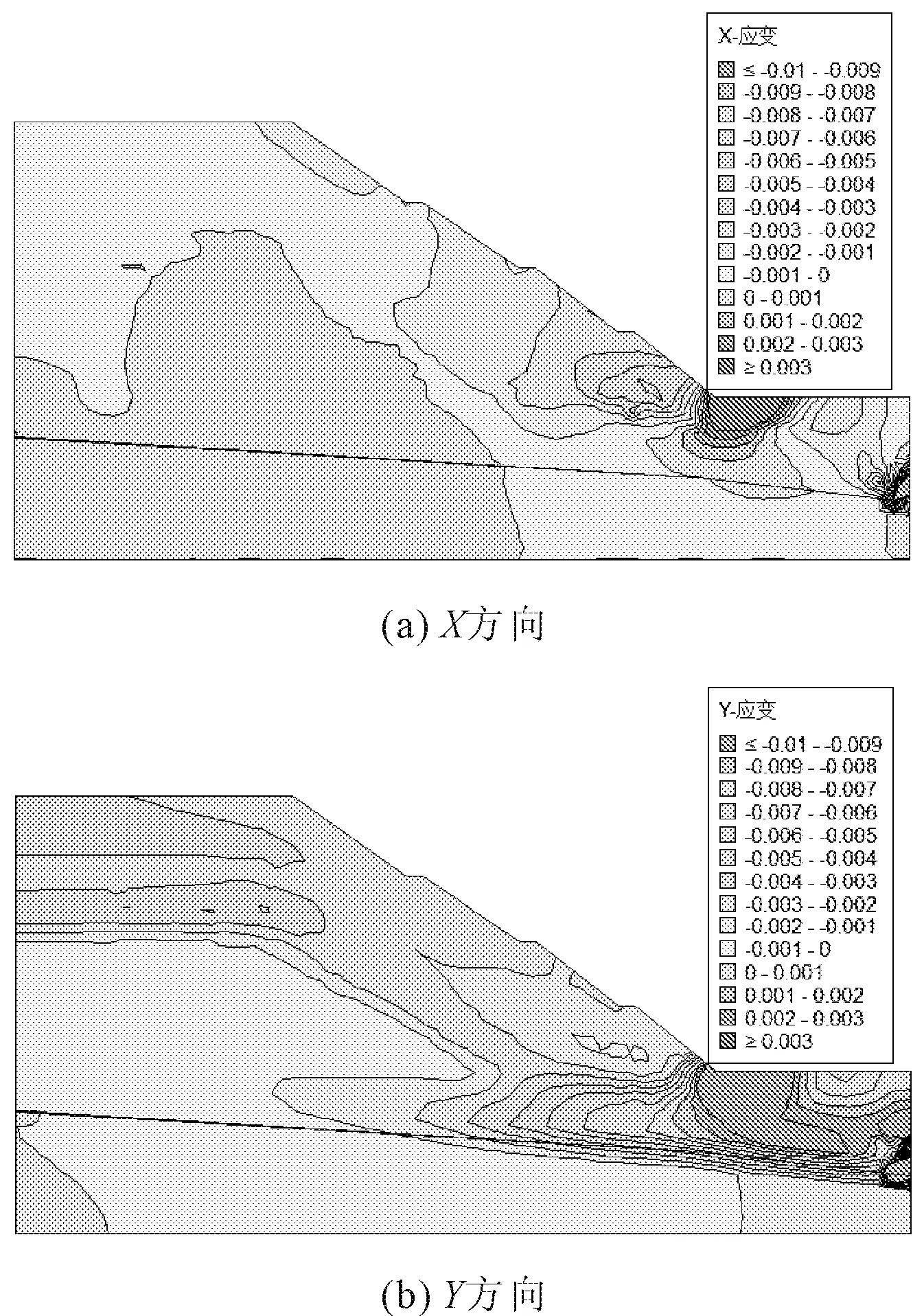
图11 长时小雨工况不同方向上应变等值线图

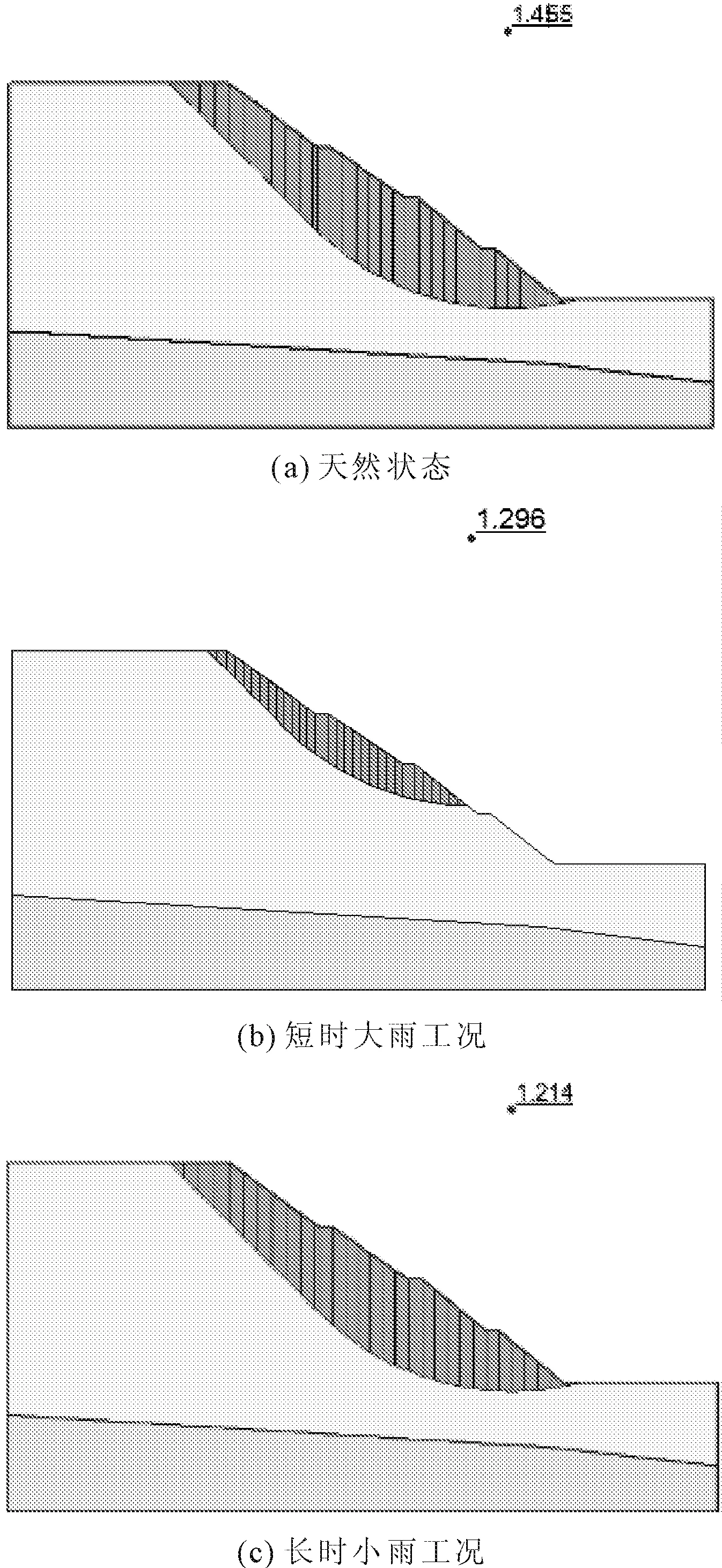
图12 不同工况边坡安全系数云图

图13为不同工况边坡安全系数时变曲线，天然状态下，边坡安全系数最终维持在1.450，边坡整体稳定；两种降雨工况下边坡稳定安全系数均呈下降趋势，在0～36 h的降雨时段内，短时大雨工况下边坡安全系数的下降幅度明显大于长时小雨工况，36 h降雨时，短时大雨和长时小雨工况安全系数分别为：1.296、1.437，降幅依次为：10.8%、1.1%，这表明雨强越大，安全系数下降的幅度也越大。短时降雨下边坡以浅层渗流为主，坡体表层暂态饱和区随降雨的进行而逐渐扩大，后期边坡安全系数下降速率迅速增加，呈陡降趋势；而长时小雨工况下，边坡安全系数在整个降雨周期内持续下降，且其下降速率先增大后减小，这与后期雨水入渗能力下降有关。

图13 边坡安全系数的时变曲线

4 滑坡预警研究

基于边坡水平和沉降位移值与安全系数的关系，研究不同工况下边坡预警的位移阈值。以ZK11为研究对象，不同降雨工况下监测点ZK11位移与安全系数呈现出双S型递减规律(见图14)，由拟合效果可知，双S型递减规律可用BiDoseResp函数来描述，具体方程如下：

(1)

上式：Fs为边坡安全系数，u为位移，mm，a、b、d、f、p为影响参数，c、e依次为第一、二个拐点。各个参数的拟合结果见图14，水平位移、竖向沉降与安全系数的相关系数分别为0.999 0、0.998 8，拟合结果良好。

短时大雨工况下，可用BiDoseResp函数描述边坡安全系数与水平位移的关系，两者呈现非线性负相关。当累计水平位移达到123 mm前应做好滑坡防护和安全预警工作。短时大雨条件下，边坡以浅层水平渗流为主，边坡浅层土体孔隙水压力快速上升，吸力下降，即：坡体累计水平位移响应周期长，易发生边坡浅层滑坡。因此，滑坡预警时应以累计水平位移指标为主，累计沉降位移指标为辅，且边坡经历短时大雨后，一定要注意发生浅层滑坡的风险。长时小雨工况下，边坡安全系数与沉降位移呈现非线性相关，两者同样可用BiDoseResp函数联系，沉降位移指标预警值为152 mm。持续降雨使地下水位逐步上升，非饱和区逐渐减小，边坡位移和孔压的影响范围逐渐向深部扩展，雨水持续入渗到边坡内部，渗流以竖向渗流为主，安全稳定系数持续下降，最终可导致降雨期间以非饱和区域为主的滑坡产生。整个降雨过程中，边坡竖向应力和应变持续增大，且影响范围也持续增大，边坡内处于压缩状态，竖向位移持续时间长，因此，长时小雨条件下，监测预警初期应以累计水平位移为控制指标，后期雨水入渗至深处，监测应侧重累计竖直沉降、并兼顾累计水平位移的发展。

图14 ZK11沉降位移和安全系数关系图

5 结 论

(1) 边坡坡体变形和累计降雨量呈正相关关系，随着降雨量的增大，边坡坡体变形增大，安全系数逐渐减小。

(2) 短时大雨工况下边坡以浅层水平渗流为主，浅层土体孔隙水压力变化快，坡脚为应力应变集中区域，易发生浅层滑坡，边坡水平位移对边坡失稳响应持续时间长。因此，应将累计水平位移作为边坡在短时大雨工况下首先考虑的失稳预警因子。

长时小雨条件下，边坡稳定性下降缓慢，雨水持续入渗至坡体内部，坡体深部孔压和应变变化显著。因此，降雨初期监测预警控制指标可选择累计水平位移，后期降雨监测应以累计沉降位移指标为主、累计水平位移指标为辅。两种工况下，在坡脚处均产生应变集中，降雨诱发多级残积土坡失稳破坏的过程中应注重坡脚的防护。

(3) 短时大雨及长时小雨工况下，可用非线性BiDoseResp函数来描述累计水平位移、竖向沉降与边坡安全系数的双S型递减趋势，前者累计水平位移预警值为123 mm，后者累计沉降位移预警值为152 mm。

(4) 降雨强度的变化对边坡稳定性的影响显著，可进一步开展不同降雨强度下边坡安全系数变化规律数值研究，构建降雨强度-持续时间-安全系数的内在联系，分析降雨诱发滑坡的临界降雨条件及预测滑坡发生的可能时间。