压力分散型锚索锚固段应力分布及影响参数分析

屈文涛，马丽娜，田 晓，史婵媛，习铁宏

(1.西安石油大学 机械工程学院，陕西 西安 710065；2.山东兖矿轻合金有限公司，山东 邹城 273515；3.中国石油长庆油田分公司勘探开发研究院，陕西 西安 710018；4.中地地矿建设有限公司，北京 100013)

近年来，虽然岩土锚固理论不断被完善，但现阶段锚固理论的发展依然落后于工程应用,传统的拉力型锚索已经不能满足工程需要[1-2]。与之相比，压力分散型锚索受力机制更加合理，降低了应力集中程度，具有较高的承载力和抗震稳定性。因此，压力分散型锚索迅速发展起来。

目前，国内外的学者们的研究主要集中于对锚固荷载传递机理研究及加固效果分析，并在锚固荷载传递机理取得一定的成果[3-7]。随着研究的深入，研究重点逐渐从拉力型锚索转移到压力型锚索，很多学者[8-11]通过数值模拟和试验得出锚索锚固段的应力分布方程及应力分布规律，但是，对于压力分散型锚索锚固段力学分布规律的研究相对较少。梁月英等[12]通过对多段扩孔压力分散型锚索拉拔的数值模拟，得出当承载体个数为3时能有效提高承载力。张勇等[13]对压力分散型锚索锚固段力学性能进行现场试验,通过对锚固段应力分布状态进行观测,根据试验结果拟合出压力分散型锚索锚固段应变分布方程和轴力分布方程。

综上所述，对压力分散型锚索锚固段应力学分布规律的研究较少，锚固理论并不完善。在压力型锚索锚固段应力分布规律的基础上，利用类比推理法得出压力分散型锚索的锚固段应力分布双曲函数模型，探讨了锚固段的应力分布规律及影响参数，并采用单一控制变量法研究了相关参数对锚固段受力分布规律的影响，为压力分散型锚索的设计及计算提供理论依据。

1 锚固段应力分布双曲函数模型

压力分散型锚索结构示意图如图1所示。在受到外部施加载荷时，压力分散型锚索将施加的集中载荷通过数根无黏结钢绞线变为数股分散载荷，分别作用在每个承载体上，且承载体均匀分布在锚固段内；再利用锚固段内的各个承载体将分散的施加载荷以拉应力的形式转化为压应力，将其传递给注浆体。此外，沿注浆体向外锚头方向，锚固段的载荷承载能力逐级衰减直至自由段，缓解了应力集中现象。

图1 压力分散型锚索结构图

为了得到理想的计算模型，根据压力分散型锚索结构示意图，将结构进行简化，得到锚固段的力学物理简图如图2所示。其中：L为相邻承载体的距离，La为锚固段长度，Pi为第i个承载体所受的拉拔载荷[14]。

图2 压力分散型锚索锚固段物理简图

假定注浆体和岩土体是理想状态下的弹性体，忽略二者自重的影响，此时单元锚固体所受拉拔载荷的作用等同于压力型锚索锚固段受力作用，其锚固段应力分布双曲函数模型可以由各单元锚索的应力叠加获得。

总结前人经验知：压力型锚索锚固段的应力分布规律属于双曲线模型[15]，且界面剪应力τ(x)、轴向力P(x)分布的函数模型分别为:

(1)

(2)

因此，压力分散型锚索锚固段应力分布双曲线模型为：

(3)

(4)

式中：xi为第i个承载板的位置。

(5)

2 压力分散型锚索锚固段受力分析

由于三承载体的压力分散型锚索具有较高的承载能力，假定式(3)、式(4)中双曲线模型中的i恒等于3，其余参数的初始值分别为：Pi=400 kN；k=0.2；La=9 m，则两相邻承载板间的距离为L=3 m。因此，锚固段的剪应力和轴向力双曲线表达式分别为：

(6)

(7)

图3和图4分别表示压力型和压力分散型锚索锚固段关于剪应力和轴力分布曲线对比图。

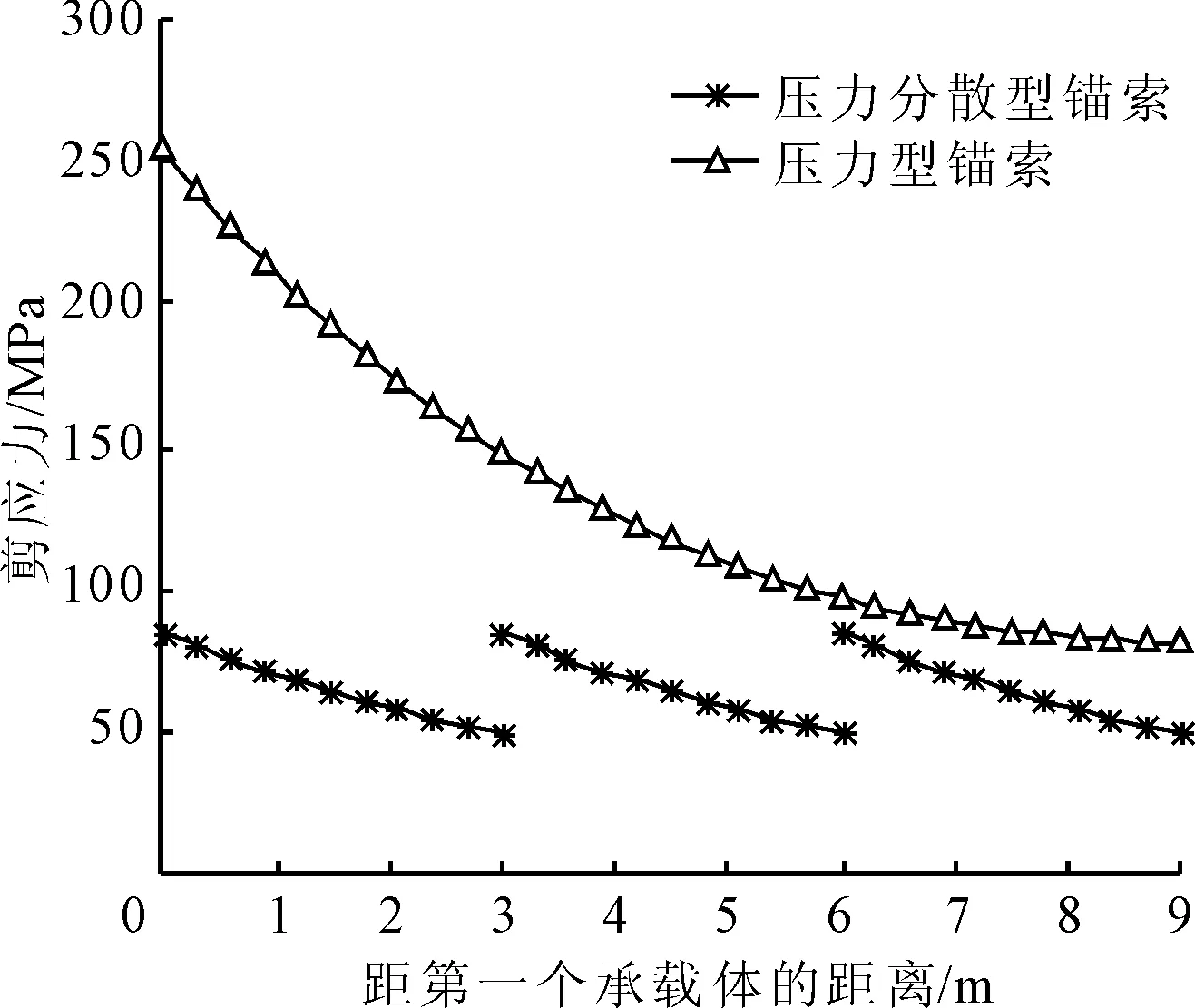
图3 剪应力分布曲线对比图

图4 轴向力分布曲线对比图

在图3和图4中，从数值分析及曲线走势可以看出压力型锚索和压力分散型锚索锚固段的应力分布具有以下特点：

(1) 压力型和压力分散型锚索的剪应力和轴向力分布规律均符合双曲函数。

(2) 压力型和压力分散型锚索的应力在承载体处达到峰值，且随着受力位置远离承载体，应力呈双曲函数减小趋势，且单元锚固体变化趋势保持一致。

(3) 压力型锚索的锚固段应力主要集中在承载体处，容易造成应力集中现象；对比压力分散型锚索，其应力分布在各单元锚索锚固段中，且峰值为压力型锚索的1/i(i为承载体的个数)，有效地缓解了应力集中问题。

3 影响参数分析

通过对压力分散型锚索的锚固段应力分布函数分析可以得出：锚固段应力的大小主要取决于三个参数，分别为拉拔载荷P，锚固体轴向刚度k和锚固段长度La。

3.1 施加拉拔载荷P值的影响

对锚固段施加不同的拉拔载荷，其值设为400 kN、600 kN、800 kN，其他参数的初值保持不变，则不同P值作用下的剪应力和轴向力分布曲线分别如图5、图6所示。

图5 不同P值的剪应力分布曲线

图6 不同P值的轴向力分布曲线

从图5、图6可以得出，随着与承载体距离的增大，剪应力和轴向力均随着锚索长度的增加而逐渐减小。具体数值分析如表1所示。

表1 不同P值下的数值分析

由表1分析得：轴向力峰值只与拉拔载荷的大小有关，且在数值上等于拉拔载荷P值的大小；随着P值的增大，轴向力和剪应力峰值均增大，同时应力的变化趋势都随之增大，能够明显增强锚固效果。因此，在保证锚固段界面抗拉以及抗剪强度范围内，可以适当地增大拉拔载荷，但仍需要避免出现锚固段的应力集中现象。

3.2 锚固体轴向刚度k对锚固段应力分布的影响

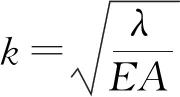
图7 不同k值的剪应力分布曲线

图8 不同k值的轴向力分布曲线

从图7、图8可以看出：随着锚固体轴向刚度的增大，剪应力的峰值增大，但轴向力峰值始终等于施加的拉拔载荷的大小。具体数值分析如表2所示。

表2 不同k值下的数值分析

随着k值的增大，剪应力和轴向力的变化范围及衰退速率都逐渐增大。同时，随着位置逐渐靠近承载体，在同一位置上，剪应力随k值的增大而增大，轴向力随之降低。k值增大，则对应锚固体的横截面积A在逐渐减小，锚固段的应力集中现象会随之增强。

因此，在工程实际施工过程中，k值应合理选择。当选取轴向刚度较小时，横截面积过大会使锚固段的剪应力过低，从而降低锚固效果；反之，较小的横截面积会出现剪应力大于界面准许抗剪强度的情况，对锚固体造成不可逆的物理破坏，从而影响锚固效果，甚至造成锚固失效。

3.3 锚固段长度La对锚固段应力分布的影响

锚固段长度的选择不仅影响锚固效果，而且与工程实际的经济效益密切相关。假定其他参数保持初始值，取La=9.0 m，10.5 m，12.0 m，即单元锚固长度为3.0 m、3.5 m、4.0 m，则不同La值作用下的剪应力与轴向力分布曲线分别如图9、图10所示。

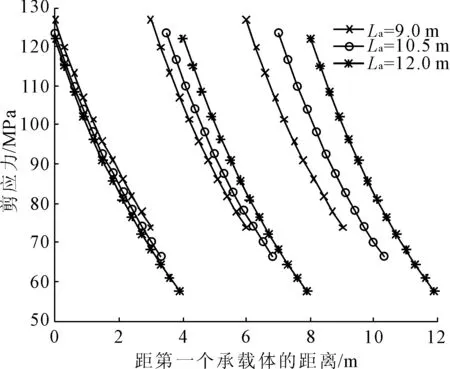
图9 不同La值的剪应力分布曲线

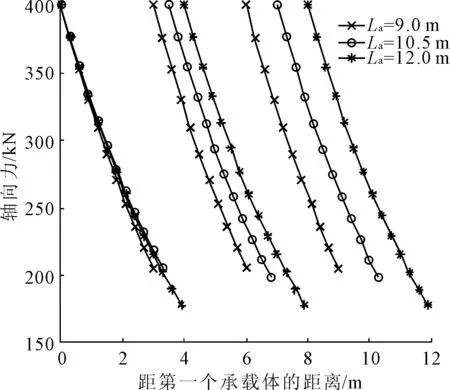
图10 不同La值的轴向力分布曲线

从图9、图10可以得出，在三个锚固单元中，剪应力和轴向力的变化趋势大致相同，变化范围并不明显，具体数值分析如表3所示。

表3 不同La值下的数值分析

通过数值对比发现，随着单元锚固长度增大，单元轴向力峰值始终不变，且剪应力峰值变化并不明显；但单元剪应力极小值均随之有减小趋势，轴向力极小值下降趋势明显。由此可见，单元锚固体的轴向力峰值与锚固长度无关，但在准许抗剪强度内，锚固体长度与锚固能力呈负相关，单元锚固长度越短，剪应力峰值越大，对应的锚固能力越强。同时，在单元锚固段内，随锚固体长度增加，剪应力的作用范围从53 MPa增大到65 MPa，且轴向力的作用范围从195 kN增大到223 kN。因此，锚固体长度的增加，导致应力的作用范围增大，使岩体受到的支护反力随之增加，进而影响锚固支护效果。

4 结 论

(1)压力分散型锚索锚固段应力分布规律为双曲函数模型。

(2)对比压力型锚索锚固段的剪应力和轴向力曲线，得出压力分散型锚索各单元体可起到分担外部荷载的作用，且载荷均匀分布在每一个锚固单元，有效避免了应力集中问题。

(3)在锚固段应力极限及许用剪切强度内，适当增大拉拔载荷和轴向刚度，锚固效果随之增强；同时，锚固段不宜过长，一方面，在准许抗剪强度内，锚固体长度越短，锚固能力越强；另一方面，过长的锚固段，会增大剪切力作用范围，使岩体的支护反力增大，不利于岩土支护；此外，在工程应用中适当的缩短锚固段长度可减少用料，增强锚固效果，具有更高的经济效益和现实意义。