基于物质点法的土体强度对边坡失稳滑动距离影响研究
宰德志,庞 锐
(大连理工大学 水利工程学院, 辽宁 大连 116024)
边坡稳定问题一直是岩土领域多年来的热点研究课题之一。数值模拟是明确滑坡失稳过程,揭示致灾机理的有效手段[1]。有限元法作为一种传统连续介质方法,常用于判断边坡的极限状态,但在处理失稳后的大变形时会遇到网格畸变问题[2]。离散元法虽然能够处理岩土大变形问题,但其内部参数的确定难度大,且进行大规模计算耗时长、效率低[3]。
Sulsky等[4]改进FLIP方法,并将其扩展到固体力学领域,建立了物质点法。为解决标准物质点法中质点穿越背景网格引起的应力振荡等问题,Bardenhagen等[5]对物质点法进行扩展,提出了广义插值物质点法(GIMP)。国内一些学者对物质点法的发展也做出突出贡献。Zhang等[6]把物质点法与有限元法耦合在一起,提出了物质点有限元法。Wang等[7]提出了隐式物质点法,改进算法精度,并将其应用在岩土领域中。
物质点法是一种完全的拉格朗日质点类方法,该方法充分发挥拉格朗日法和欧拉法各自的优点,能够准确、高效地模拟岩土材料的大变形行为。本文采用物质点开展边坡失稳状态和滑坡的全过程模拟,并详细分析土体强度对滑动距离的影响,为边坡灾害的防治提供参考。
1 物质点法基本理论
物质点法采用拉格朗日质点和欧拉网格来双重描述离散域,将连续体离散成携带材料信息的一系列质点,如图1所示。在每一计算时步内,质点和计算网格固连,避免了数值计算中非线性对流项的产生;计算时步结束后,丢弃已变形的计算网格,采用新的未变形计算网格,从而避免网格畸变。其中网格仅用于动量方程的求解和空间导数的计算,质点携带该区域网格的所有信息[8]。

图1 物质点法示意图
1.1 运动方程
(1) 动量方程[9]:

(1)

(2) 引入虚位移,并在连续体域内积分,得到更新拉格朗日格式的弱形式[8]:

(2)

(3) 将连续体密度近似,把积分弱形式转化为求和的离散形式[8]:
(3)
式中:np为物质点总数;mp为物质点p的质量;h为引入的假想边界层厚度;带有下标p的物理量表示物质点p的变量。
(4) 依据牛顿第二定律,分类、结合、化简得到背景网格结点的运动方程[8]:
(4)

1.2 方程求解
标准物质点法的求解格式有三种[8],分别为USF、USL和MUSL。根据应力更新时刻的差异,划分为USF和USL两种求解格式,前者在每个计算时步开始时更新应力,后者在计算时步结束时更新应力。MUSL是基于USL改进的一种求解格式,将更新的质点动量映射回背景网格后再计算节点速度。MUSL具有良好的能量守恒性,故本文采用MUSL求解格式。
当网格尺寸较小时,标准物质点法中质点会穿越背景网格,引起数值噪音,产生应力振荡[10]。相比于标准物质点法,广义插值物质点法能有效减轻应力振荡,但会显著增加计算时间,且随着质点数目的增加,计算时间增加的趋势变快。基于计算效率考虑,本文的计算方法采用标准物质点法。针对运动方程是关于时间的二阶常微分方程,本文利用中心差分法[11]求解,计算时间步长小于临界时间步长,具体要求满足式(5)[8]。
(5)
式中:α为时间步长因子,本文取0.8,Δl为背景网格长度;cp为压缩波波速,与岩土材料特性有关。
1.3 本构模型

(6)

Mohr-Coulomb(MC)屈服面在π平面上为不规则的六边形,在六个顶点处法线方向不唯一,导致顶点处的数值求解困难。本文采用的Drucker-Prager(DP)屈服面在主应力空间中为圆锥面,在π平面上为圆形,便于求解,其屈服函数满足式(7)[12]:
(7)
式中:J2为第二偏应力张量不变量;I1为第一应力张量不变量;qφ与kφ为材料常数。本文采取DP屈服面在π平面上内接MC屈服面,见图2。材料常数与黏聚力c及内摩擦角φ的关系如式(8)[12]。

图2 π平面上MC屈服面和DP屈服面的关系图[8]
(8)
在DP模型中,剪切屈服采用非关联塑性流动法则,其势函数Ψs的关系满足式(9)[8]:
(9)
式中:qΨ为材料常数,由剪胀角ψ确定,二者的关系和qφ与φ之间的关系相同。由于材料满足塑性不可压缩条件,剪胀角取为0。拉伸屈服采用关联流动法则,其势函数Ψt的表达式满足式(10)[8]:
(10)
2 程序验证
Bui等[13]通过堆积干燥铝棒坍塌试验模拟砂土的失稳过程,并采用光滑粒子流体动力学(SPH)方法对其进行数值模拟,同时对黏土失稳的大变形过程开展了分析。本节应用物质点法模拟上述试验和粘土的大变形过程。程序采用清华大学张雄教授课题组开发的MPM3D-F90[8],并在其基础上进行了改编,编译环境为Microsoft Visual Studio 2010,数据后处理采用Tecplot 360 EX 2018 R1。
2.1 干燥铝棒坍塌试验模拟验证
为了便于对比试验结果,模型尺寸及材料参数和Bui等[13]的数据保持一致,即模型长200 mm,宽2 mm,高100 mm,材料参数如表1所示。模型采用40 000个物质点离散,刚体边界采用10 128个物质点离散,模型和刚体边界之间采用刚柔接触。相邻物质点间距为1 mm,背景网格尺寸为2 mm。模型左(X=-8 mm)、底(Y=-8 mm)边界采用固定边界,右(X=500 mm)、上(Y=120 mm)边界采用自由边界,平面法向两边界(Z=0 mm、Z=2 mm)为对称边界。

表1 干燥铝棒材料参数
图3(a)为Bui等通过试验得到的干燥铝棒坍塌最终构型图,图3(b)为利用物质点法数值模拟得到的最终堆积形态。可以看出,利用物质点法模拟的堆积物最终形态及滑动区域与非滑动区域的分界线和试验结果均吻合较好,从而验证了该程序模拟砂土大变形问题的有效性。
2.2 黏土大变形模拟验证
黏土模型长4 m,宽0.02 m,高2 m。土体材料参数与Bui等[13]数值模拟中保持一致,具体参数如表2所示。模型采用40 000个物质点离散,刚体边界采用5 728个物质点离散,相邻物质点间距为0.02 m,背景网格尺寸为0.04 m。模型左(X=-0.16 m)、底(Y=-0.16 m)边界采用固定边界,平面法向两边界(Z=0 m、Z=0.02 m)采用对称边界,右(X=5 m)、上(Y=2 m)边界为自由边界。

图3 铝棒坍塌堆积形态图

表2 黏土材料参数
图4(a)图为Bui等采用SPH方法进行数值模拟得到的黏土塑性偏应变云图,图4(b)图为采用物质点法进行数值模拟得到的累计等效塑性应变云图。从图中可得,滑动带的位置、形状、宽度及稳定后的最终构型基本保持一致。同时,两种方法模拟黏土失稳的过程也具有较高相似性,即相同计算时刻,黏土失稳形态相似。这表明该程序能够合理地模拟黏土大变形问题。

图4 SPH模拟图[13]与MPM模拟图
3 影响因素分析
边坡滑动距离是指坡脚到失稳后滑坡前缘的距离,是边坡安全控制的重要因素之一。针对边坡的滑动失稳,分析了不同坡角(30°、45°、60°、75°)情况下边坡的内摩擦角和黏聚力对滑动距离的影响规律。边坡几何尺寸如图5(以45°坡角为例)所示,底部为固定边界,上部为自由边界,其余为对称边界。坡体材料参数汇总于表3[8]。
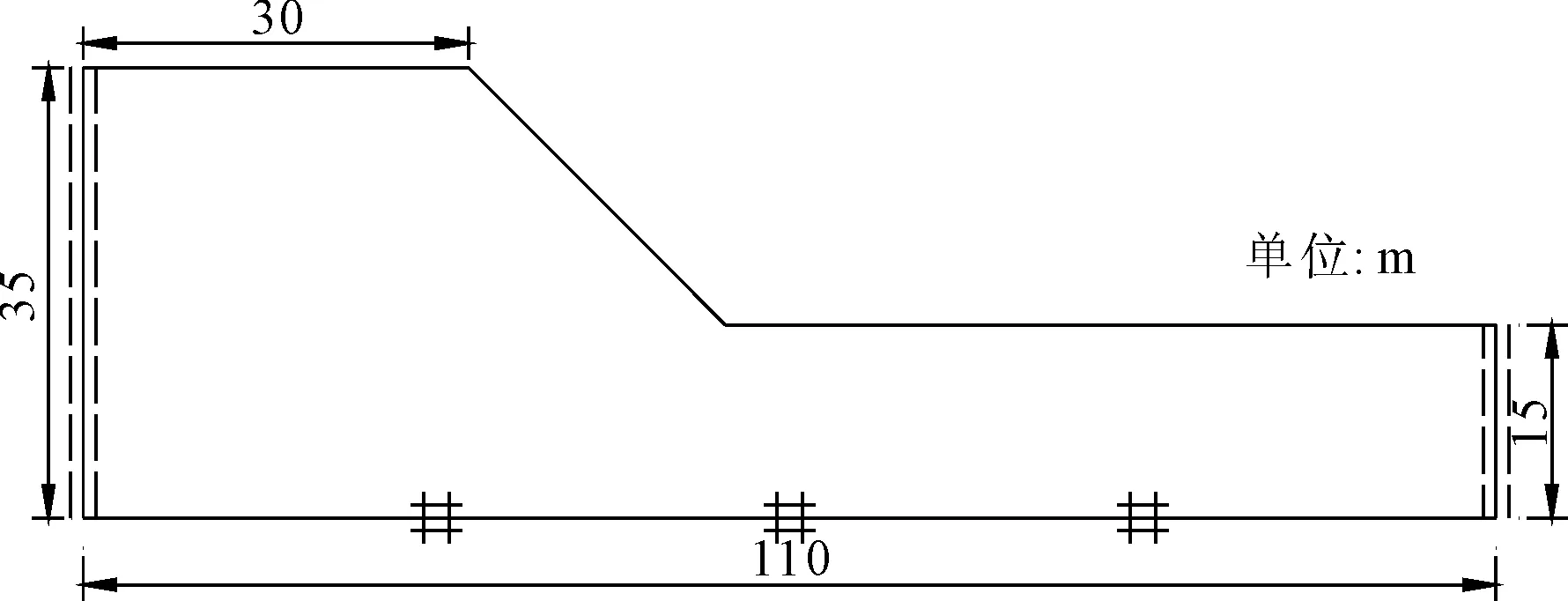
图5 边坡几何尺寸

表3 边坡土体参数
基于滑动距离和边坡形态,以45°坡角的边坡为例,确定合理的相邻物质点间距[14]。边坡模型见图5,内摩擦角取20°,黏聚力为5.0 kPa。采用2 460、9 820、15 475和39 240个物质点离散连续体,其对应的相邻物质点间距分别为1.00 m、0.50 m、0.40 m和0.25 m。数值模拟得到的构型图见图6,图中颜色差异代表不同的等效塑性应变值。采用上述物质点数进行数值模拟得到的滑动距离分别为8.0 m、16.6 m、17.4 m、18.1 m,计算耗时分别为83 s、340 s、678 s、6 848 s(基于2.9GHzCPU(Intel(R) Core(TM)i7-10700 CPU)和16 GB内存计算机)。考虑边坡最终构型、滑动距离及计算耗时,采用15 475个物质点进行数值模拟,能够保证结果的精度且计算效率高。因此,在后续参数研究中,相邻物质点间距取0.4 m。
3.1 内摩擦角
固定黏聚力值为5 kPa,在10°~35°范围内取不同内摩擦角,分析不同坡角情况下,内摩擦角与滑动距离的关系,结果如图7所示。可以看出,边坡失稳后其滑动距离与土体内摩擦角呈现负相关性。坡角为30°的边坡在内摩擦角增至25°时滑动距离为0,而坡角为45°的边坡在内摩擦角增至35°时滑动距离为0。内摩擦角较小(<25°)时,滑动距离对其变化比较敏感;内摩擦角较大时,滑动距离的变化程度减小,趋于常值。内摩擦角一定时,边坡越陡,失稳后的滑动距离越大,其可能造成的危害愈大。数值模拟过程中,内摩擦角10°时,滑裂面底部低于坡脚高度,失稳模式类似于深层滑坡,且坡脚以上边坡发生巨大位移;内摩擦角35°时,陡坡滑动距离较小,缓坡无滑动,只是在边坡的中上部发生较大塑性应变。同时,失稳边坡达到稳定状态后,边坡倾角随内摩擦角增大逐渐增加,但始终小于后者。

图6 不同物质点数目边坡形态图

图7 内摩擦角与滑动距离关系图
3.2 黏聚力
固定内摩擦角值为20°,在0 kPa~24 kPa范围内取不同黏聚力,分析不同坡角情况下,黏聚力与滑动距离的关系,结果如图8所示。可以看出,边坡失稳后其滑动距离与土体黏聚力呈现负相关性。坡角为30°的边坡在黏聚力增至8 kPa时滑动距离为0,而坡角为45°的边坡在黏聚力增至24 kPa时滑动距离为0。在黏聚力较小的初始阶段(<6 kPa),黏聚力对滑动距离的影响比较明显;在黏聚力较大的末尾阶段(>18 kPa),黏聚力对滑动距离的影响趋于稳定。黏聚力一定时,坡角对滑动距离的影响颇大,坡度越大,滑动距离越大。数值模拟过程中,黏聚力增至24 kPa,形成了坡脚到坡顶的贯穿滑裂带,但等效塑性应变值总体偏小,仅在陡坡中出现较小的滑动距离,未发生明显的塑性流动现象。
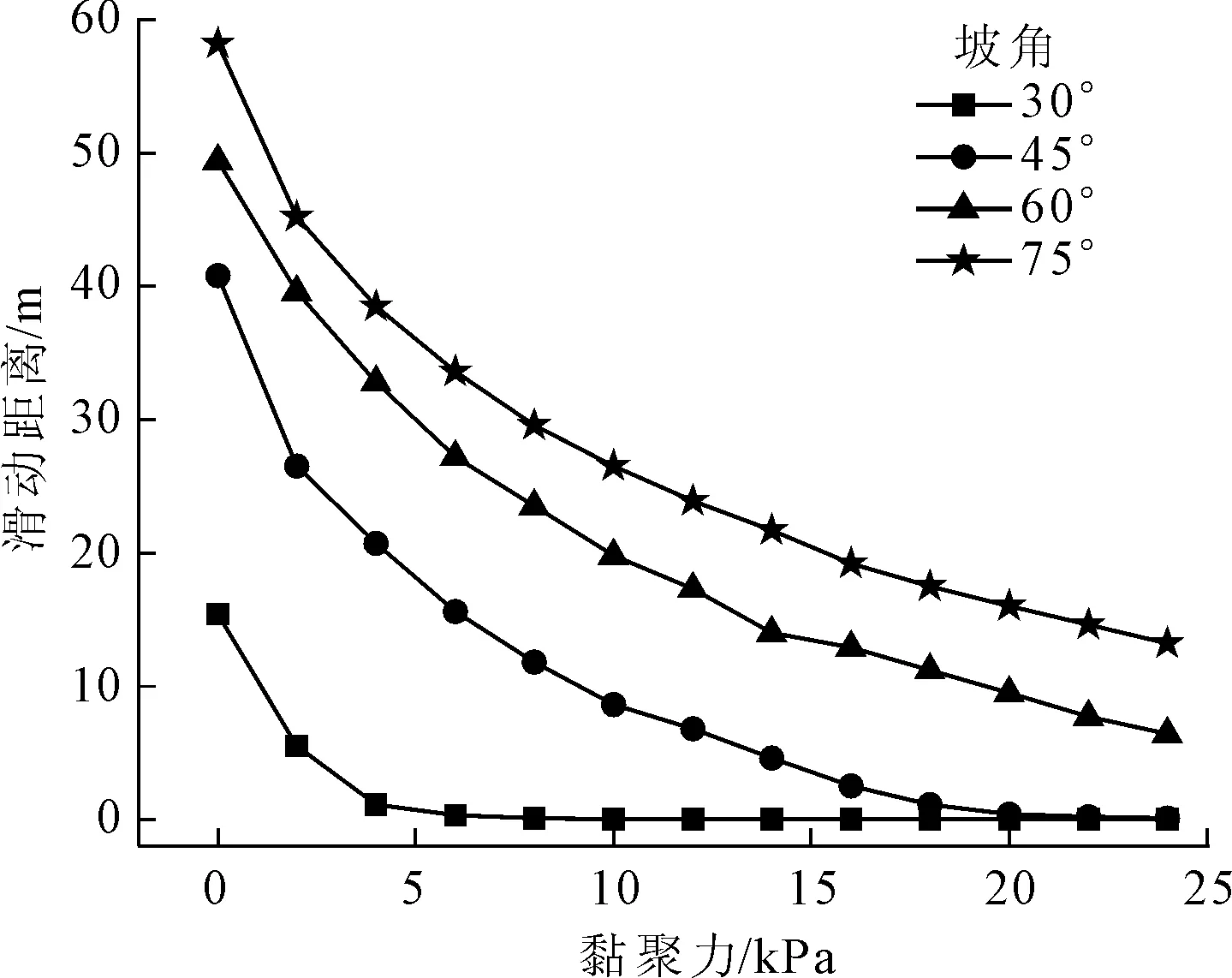
图8 黏聚力与滑动距离关系图
4 结 论
(1) 合理地选取离散点数和间距,对物质点法数值模拟的结果至关重要。建议根据边坡最终构型、滑动距离及计算效率选取合适的相邻物质点间距。
(2) 滑动距离随土体强度的增大逐渐减小。
(3) 边坡在地震荷载作用下的稳定性也是工程设计关注的重点问题,后续工作将基于物质点法深入开展边坡动力失稳机理和滑动过程研究。

