面向脑机接口个体差异的滤波器组设计方法及其模型研究
李子波,唐荣年,谢小峰
(海南大学机电工程学院,海南 海口 570228)
脑机接口(Brain⁃Computer Interfaces,BCI)将脑信号转换为可传达用户意图的输出[1],为大脑控制外部设备提供了一种新颖的连接方式,例如轮椅,假肢和计算机[2].此项研究能够为患有严重运动障碍的人开发出一种新的交流和控制的方式,有助于提高运动障碍者的生活[3].不同的BCI系统设计出几种脑电信号(Electroencephalogram,EEG)模式,其中基于运动想象(Motor Imagery,MI)的BCI系统可以将想象身体运动转换为控制命令[4].在处理运动想象的EEG信号方法中,共空域模式(Common Spatial Pattern,CSP)是非常有效的特征提取方法之一[5-6].CSP算法不仅可以从运动想象的信号中提取出最具有判别性的特征,而且可以提供EEG信号通道选择的权重信息[7],但CSP算法的效果受滤波器筛选的频带信息影响.值得注意的是,在运动想象任务中,在特定的频带范围蕴含非常重要的EEG信号信息,例如alpha波段(8~13 Hz),beta波段(14~30 Hz).因此,选择合适的频带信息尤为重要.
针对CSP算法和CSP变体算法的研究受到广泛的关注,滤波器组共空域模式(Filter Bank CSP,FBC⁃SP)使用零相位的切比雪夫Ⅱ型滤波器将原始信息滤波为多个子带,并使用互信息系数自动选择特征[7];子带共空域模式(Sub⁃Band CSP,SBCSP)与FBCSP相似,在信号的多个子带上使用Gabor滤波器,然后基于子带分数融合技术选择特征[8];自适应滤波器组共空域模式(Adaptive Filter Bank CSP,AFBCSP)可以基于Fisher比率来自适应选择特定于对象的区分性频带[9].虽然上述研究方法在滤波器组设计时都包含了al⁃pha和beta波段,但是滤波器组划分出所有的子频带都是相等权重,即与运动想象相关的频带信息没有被突出表达.由于个体的差异,导致不同实验对象的重要频带范围会有波动,如图1所示,展示了2个实验对象在想象右手运动的时频图存在差异.图1红色框选择范围表示重要频带,由于个体区别使得alpha波段和beta波段在每个个体上的表达存在差异,从而影响信息的表达.

图1 不同对象在运动想象时出现的频段不一致现象
综上所述,如何突出表达与运动想象相关的频带信息以及消除由于个体差异导致重点频带范围波动尤为重要.笔者针对上述问题设计出一种新颖的滤波器组设计方法,不仅能够突出表达alpha和beta波段的信息,而且还能够在一定程度上改善由于个体差异导致的重要频带范围波动的影响,提升模型的稳定性.
1 试验方法
1.1数据来源实验中使用的n道EEG数据为BCI竞赛第IV期的运动图像数据.BCI竞赛IV的数据集IIa来自9名受试者,执行4种类型的运动想象任务(右手、左手、脚和舌头想象运动).记录的信号由22个脑电图通道组成,通道构型如图2a所示.实验方案如图2b所示:

图2 电极分布与时序方案图
1)在初始时间(0~2 s),发出短的声学警告音;
2)2 s后,屏幕上出现了一个指向左、右、下或上的箭头提示,时间为2~3.25 s,激发受试者进行运动想象任务,直到6 s固定十字从屏幕上消失;
3)有1.5 s短暂休息.
处理数据的时间间隔限定在被试执行运动想象任务的3.75~5.75 s之间.对于每个受试者和运动想象任务,有72项训练和72项测试试验.因此,每个受试者的训练试验和测试试验总数都为288次,EEG信号采集,采样频率为250 Hz.
1.2分析方法设计一种新的滤波器组方法,如图3预处理部分所示,将原始的EEG信号划分为多个子频带.在粗特征提取部分,使用CSP算法分别对多个子频带提取特征.虽然该滤波器组丰富了数据表达,同时也会导致信息冗余.采取3种精特征筛选方法(组稀疏(Group Lasso)、基于极限学习机的自编码器(ELM_AE)、互信息(Mutual Information))进一步处理,最后使用LDA建立模型.
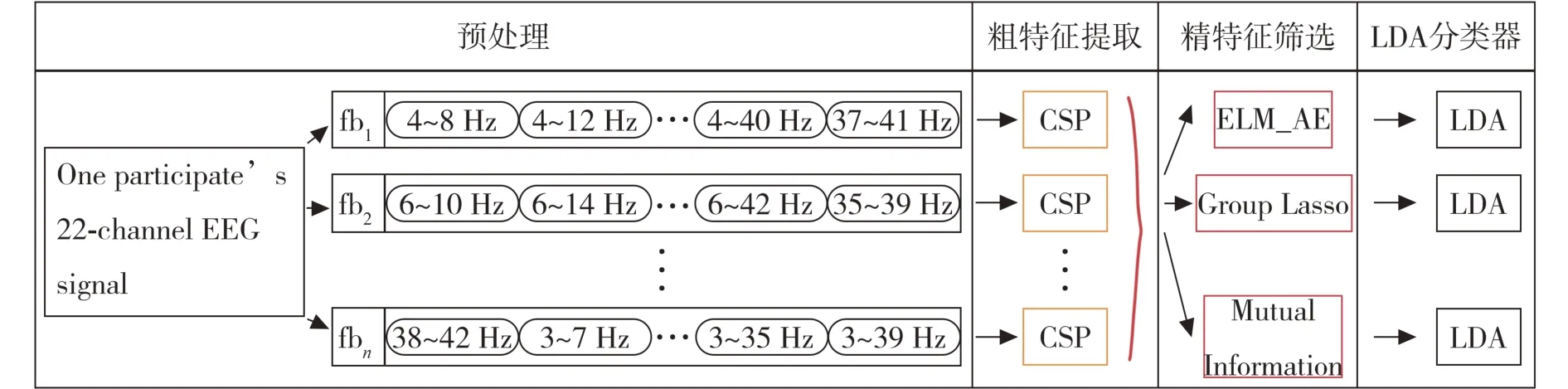
图3 滤波器组设计方法结构图
1.2.1滤波器组设计方法基于运动想象的多通道的脑电信号可以表示
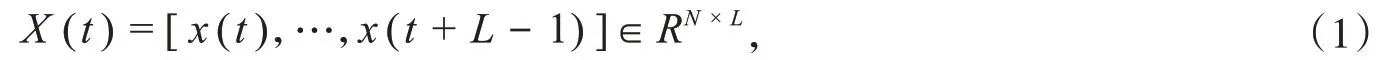
L和N分别表示采样点个数和通道数,

设计了一种全新的滤波器组方法,以4 Hz为间隔将4~42 Hz频带范围信号滤波为150个子频带,如图4a所示,即[4~8 Hz,4~12 Hz,…,4~40 Hz,3~7 Hz];[6~10 Hz,6~14 Hz,…,6~42 Hz,35~39 Hz];…;[38~42 Hz,3~7 Hz,…,3~35 Hz,3~39 Hz].从图4b可以看出,alpha和beta波段占据很大比例,使重要频带信息得以突出表达,并且2个核心频带周围的信息也被强调,可以在一定程度减缓由个体差异产生的核心波段波动的影响.

图4 滤波器组结构图与频带占比图
1.2.2CSP算法粗特征提取通过上述滤波器组将原始脑电信号分解为多个子频带,使用空域滤波器矩阵W分别从每个子频带中提取特征.对于二分类问题.CSP算法可以在最大化一类方差的同时最小化另外一类的方差,因此空域滤波器可以通过最大化最小化目标函数得到[7]

其中,Ci表示属于第i类EEG数据的协方差矩阵的算术平均值.
F表示CPS特征

1.2.33种特征精筛选方法多个子频带的CSP粗特征提取会增加冗余信息,因此分别采取3种降维和特征选择的方法进行特征精筛选.
自编码器算法降维 极限学习机(ELM)是单隐藏层前馈网络(SLFNS),尽管采用了随机投影,但在大多数情况下,ELM的性能都优于反向传播神经网络[10].与一般的多层感知机相比,ELM具有非梯度优化的特点,并且计算成本通常要低得多[11],得益于其优秀性能,近年来针对ELM的研究被人们广为关注[12-14].由于多频带所提取出的特征信息的高维度以及存在冗余,采用基于ELM的自动编码器网络对多频带CPS
特征进行编码压缩,ELM_AE的表达形式为

其中,h(fi)∈RNh×1表示隐含层为Nh的输出,a和b表示激活函数的参数,在[-1,1]范围内随机生成.AE网络的解码部分

其中,β=H†F解出.因此可以获得自编码器降维的特征S_AE

互信息熵特征选择 给定初始数据集合F(n维特征),寻找一个子集S属于F并且拥有从原始数据集合筛选出的K个最大互信息的特征[7].2个随机变量的互信息定义

对于d维随机变量X,可以表示为X={x1,x2,…,xd},其信息熵计算

对于随机变量X和Y的条件熵计算

以互信息熵值作为筛选依据,选择前K个互信息熵的最大的特征构成特征子集S_MI.
组稀疏特征选择 通过在目标函数中加入L2或者L1范数正则化约束条件,可以更容易获得稀疏解,是一种特别适用于高维问题的高效算法[15].由于稀疏正则化的优秀性能,其被广泛应用于图像的处理[16]以及神经网络的结构优化以及对EEG信号的特征筛选.
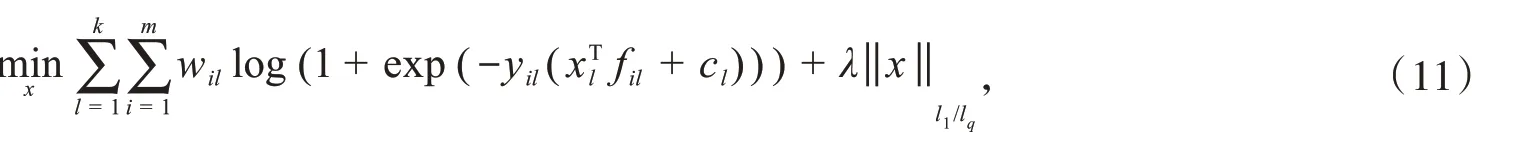
其中,fil表示对第l类的第i个样本,wil表示对应于fil的权重信息,yil是fil的响应,cl是第l类的截距,x表示待求解.通过对上式目标函数的求解,完成对多频带CSP特征的筛选得到特征集合S_GL.
1.2.4LDA分类模型LDA模型用于对低维数据的分类,LDA是一种有监督的方式,通过线性变化最大化类间距离的同时最小化类内距离[17],通过降维处理和特征选择方法对特征进行筛选,因此用LDA建立分类模型.


使用LDA分别对上述3种精特征筛选方法提取到的特征集合S_AE,S_GL,S_MI分别进行建立辨识模型.
2 结果与分析
2.1CSP粗特征提取结果以实验对象一的左右手运动想象为例,挑选出的18个子频带和4~42 Hz总频带的CSP特征的大脑拓扑图,如图5所示.左手/右手运动想象主要分布在C3和C4通道所在的脑域,4~42 Hz和18个频带的空域滤波器所提取出的特征有效的区分出C3和C42个部分,说明了CSP算法在这些子频带粗提取出的特征是有效的为下述的信号处理提供了保障.

图5 2008年BCI竞赛数据集中的18个子频带以及4~42频带对应CSP脑部拓扑图(以左右想象为例)
2.23种精特征筛选结果分析
2.2.1自编码器筛选结果图6b~e为二维CSP特征图.图6a,f~k为自编码器压缩提取后的二维特征图.图6f~k所示4个类别两两之间的精筛选特征信息呈现出较为明显的可分性能,并与图6b~eCSP粗提取出的特征相比,图6a所示自编码器处理后的特征更加可分.表明经过自编码器处理后能够在CSP粗提取特征的基础上精提取出更加有效的特征信息.

图6 CSP和AE二维特征图
2.2.2组稀疏互信息熵筛选结果图7展示了组稀疏和互信息熵2种特征选择方法在CSP粗特征提取后精筛选特征的位置分布.2种筛选方法在0~150维所选择的特征分布相似,但是互信息熵在150~300维未选择特征,可能丢失部分重要频段的信息,而组稀疏则选择了更多重要的特征.
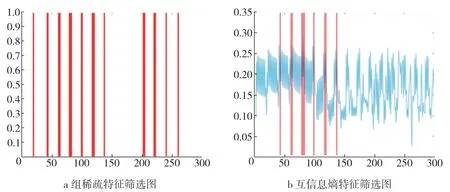
图7 组稀疏及互信息熵特征筛选图
2.3预测结果为了验证本文所设计滤波器组的效果,将其与常规的滤波组方法进行比较,常规滤波器组是将4~40 Hz的EEG信号等权重划分为[4~8 Hz,8~12 Hz,…,36~40 Hz].表1中A表示本文所提出的4~42 Hz滤波器组方法,B表示4~40 Hz均等滤波器组方法.
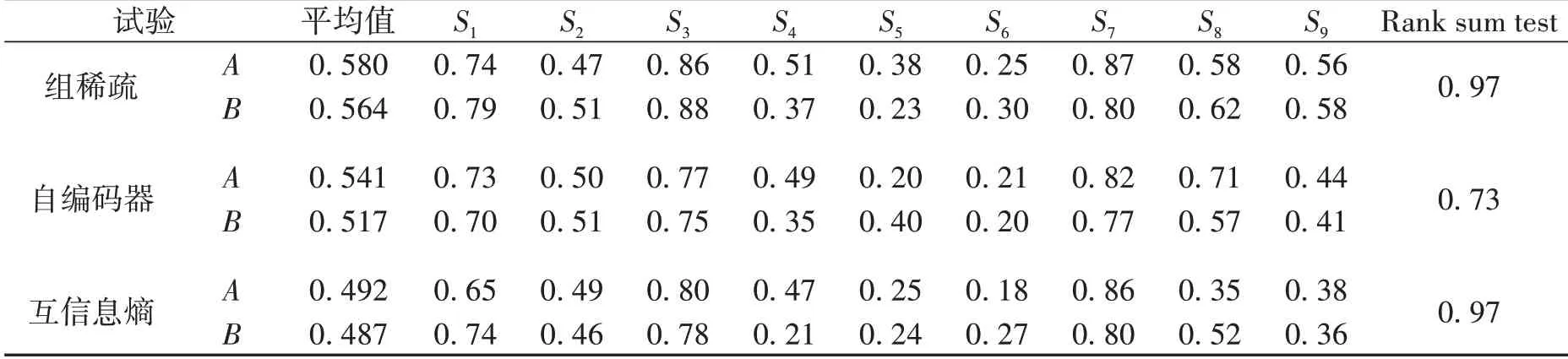
表1 分类结果(Kappa值)对比
表1为3种精特征筛选方法分别在2种滤波器组结构下的分类结果.结果表明在相同的精特征筛选方法下,本文所提出的滤波器组方法的结果都高于4~40 Hz均等滤波器组的结果,说明本文所提出的滤波器组设计方法的有效性.秩和检验的结果显示2种方法无统计显著性,这可能是由于实验样本量少以及部分对象结果极值导致的.
图8分析了3种精特征筛选方法在本文所提的滤波器组的效果.除了在实验对象8以外,组稀疏的识别效果均是最优,这可能是由于本文提出的滤波器组方法提升了数据的维度,而组稀疏在处理高维数据有着优秀的性能.因此,本文以结合组稀疏所建立的模型作为最终的识别方法.
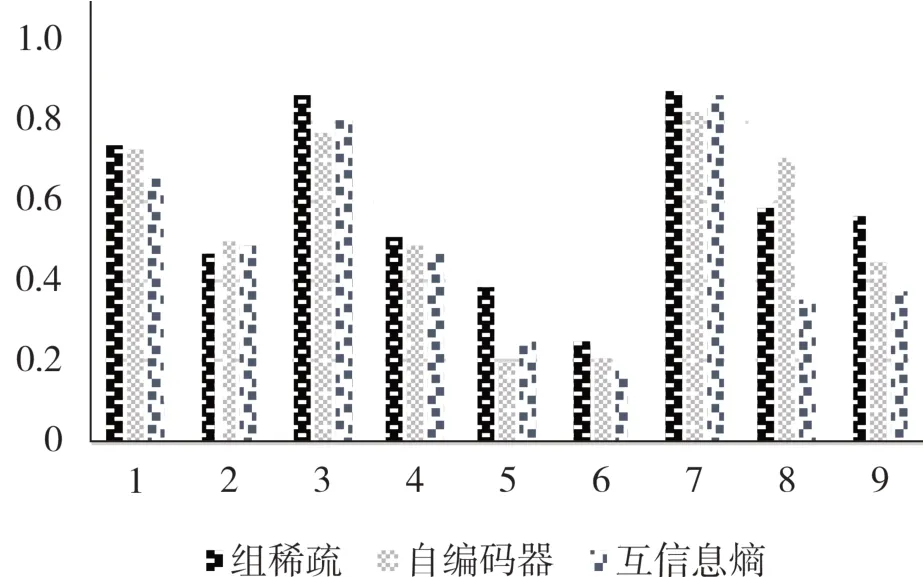
图8 3种精筛选方法建模结果图
为了进一步说明本文所提方法性能,将其与竞赛前三名以及近年基于该数据集的结果进行比较.
表2为本文方法在2008年BCI竞赛数据集上的分类结果.由表2可以看出,本文基于滤波器组设计方法的模型的分类精度达到0.58,高于竞赛前三名的预测Kappa平均值0.57(P=0.97),0.52(P=0.571)和0.31(P=0.005),但分类精度略低于SSDT_KNN(KNN结合特定对象的决策树模型)的0.61(P=0.85)[18]和ESVL(集成支持向量学习)[19]的0.60(P=0.596).SSDT_KNN将数据投影到目标空间,并训练4个KNN模型用于构建决策树模型;ESVL需要计算先验概率和多个特征,训练3个SVM分类器组合用以预测.相较于SSDT_KNN和ESVL需要训练多个分类器,本文设计的方法则不需要.结果表明了本文提出的滤波器组设计方法能够突出强调与运动想象相关的频带信息表达,并且可以在一定程度消除个体差异导致的频带波动问题,提供了一种稳定的识别方法.
3 小结
面向脑机接口的运动想象问题,笔者分析研究了运动想象的频带选择问题,设计出一种新的滤波器组方法.针对该滤波器组的特性,按照粗特征提取和精特征筛选的方法测试了该滤波器组的效果,最终预测Kappa平均值为0.58,具有优秀的分类性能.实验结果表明,所提出的方法能够突出强调alpha和beta波段的信息,并且能够在一定程度上消除由于个体差异导致关键频带范围波动的问题.

