基于动态约束模型的贝叶斯网络结构优化算法
李沛然,刘 琨,张 育,任 佳,崔亚妮
(海南大学信息与通信工程学院,海南海口,570228)
作为概率图模型的典型代表,贝叶斯网络(Bayesian Network,BN)是不确定知识表示和推理的重要理论工具.从样本数据中学习获得高质量的BN模型决定了对复杂系统认知的准确性.传统BN结构学习方法主要有基于约束(Constraint⁃Based,CB)的学习方法[1]和基于搜索(Score⁃and⁃Search,SS)的学习方法[2]2类.基于CB的学习方法主要有PC算法[3]、最大最小父子节点(Max-Min Parent Children,MMPC)算法[4]、最大权重生成树(Maximum Weight Spanning Tree MWST)算法[5]以及构建马尔科夫覆盖[6-8]等.基于SS的学习方法主要包括爬山算法[9-10]、遗传算法[11]和蚁群算法[12-13]等.上述2种学习方法虽然适合贝叶斯网络的结构学习过程,但是各自存在局限性.文献[14]研究结果表明,将2种方法结合得到的混合学习方法能够有效平衡搜索范围和搜索效果,提高BN结构学习的速度.在混合算法中,将约束方法与一些智能优化方法相结合进行结构的寻优是当前的研究热点.刘彬[12]等通过MWST初始化网络结构,然后运用蚁群结合K2进行节点序列寻优,提出一种MWST-ACO-K2算法用于BN结构学习;刘浩然[15]等提出一种IWOA算法,该算法利用MMPC结合爬山算法生成初始种群,进而运用改进的鲸鱼优化策略进行种群搜索.
在研究过程中,粒子群(Particle Swarm Optimization,PSO)算法[16]因为更新方式简单、采用并行运算求解方式、算法收敛速度更快的特点,所以逐渐被应用于BN结构的优化过程.但是BN采用二进制编码方式,传统粒子群算法无法与BN结构学习兼容,因而需要对粒子群的更新公式进行适应性优化.有学者提出将离散PSO算法或二进制PSO算法应用到BN结构学习中,例如Wang[17]等利用二进制粒子群优化方法对网络结构矩阵进行了扁平化,重新定义了粒子的速度和位置;李晓林[18]等提出了一种运用极大似然树初始化粒子群并基于免疫理论改进的二元粒子群优化方法,将粒子群优化算法与BN结构学习融合;李国梁[19]等提出了一种基于最大信息量的PSO算法,利用混沌映射的方法使邻接矩阵表示BN网络结构,通过近似的方式将所有的计算结果映射到0~1值中;范瑞星[20]等通过将差分变异算法与离散粒子群相结合,并通过自适应反向学习策略对初始种群进行有目的地扩充,达到提升寻优效率和收敛精度的效果;Liu[16]等将粒子的位置视为相关边缘存在的概率,将速度视为对相关边存在概率的增减,从而找到一种从连续搜索空间中更新粒子的方法,但是其本质依赖于对粒子群结果的合理映射.虽然上述文献基于改进粒子群方法获得了合理结构,但CB阶段对搜索空间约束固化,导致学习速度较慢,并采用映射的方式使得多种更新对应一个解结构,降低了结果对更新过程的敏感度,导致学习精度难以保证.还有研究者将PSO与其他优化算法相结合产生新的更新方法.Gheisari[21]等提出了一种改进PSO参数的结构学习方法,将PSO与遗传算法的更新方法相结合,使PSO应用于BN结构学习,但由于其初始粒子是随机生成的,忽略了对初始粒子的合理约束,使得BN结构学习精度不高;Li[22]等以MMPC建立无向图构建初始粒子群,同样采用GA与PSO相结合的方式进行结构更新;李俊武[23]等以MWST生成初始网络,通过布谷鸟与粒子群相结合的CS-PSO混合算法进行BN结构学习;Aydilek[24]运用元启发式算法,得到一种萤火虫-粒子群(HEPSO)优化算法.综上所述,许多学者都希望借助粒子群算法的全局寻优能力,但是面对PSO算法容易陷入局部最优的问题,都没能给出一个合理的解决方案.
基于粒子群的BN结构学习虽然具有算法复杂度相对较低、收敛速度快、并行效率高的特点,但是也普遍存在难以控制学习精度以及容易早熟陷入局部最优的缺陷.因此,建立前期的合理约束和早熟识别工作就显得尤为重要.针对上述问题与需求,笔者提出了一种基于动态约束模型的贝叶斯网络结构优化算法.该方法将马尔科夫覆盖(Markov blanket MB)与PSO相结合,首先设立动态阈值通过互信息(Mutual Information,MI)约束搜索范围,运用条件独立性检验(Conditional Independence,CI)构建马尔科夫覆盖,初始化粒子群缩小解结构搜索空间规模,然后通过重新定义粒子群的更新机制搜索最优结构空间,解决了粒子群在贝叶斯网络结构更新上的难题,同时提升搜索精度,最后采用计数器配合更替机制由新粒子替代部分质量较低的原始粒子,对算法进行早熟干扰,防止过早收敛导致结果陷入局部最优.
1 基本方法简述
提出了基于动态约束的马尔科夫覆盖与粒子群相结合的MB-PSO方法,全文算法过程如图1所示.
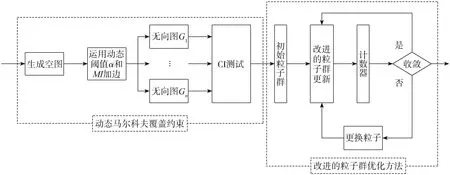
图1 基于动态约束模型的贝叶斯网络结构优化算法流程图
如图1所示,首先设立动态阈值,通过计算不同阈值下各节点的马尔科夫覆盖得到多个无向图结构,然后根据Jiang[6]等提出的CRAE算法进行定向,可以构造出复杂度不同的初始粒子,为粒子群搜索过程提供种类丰富的初始网络,最后以BIC评分作为适应度值,通过改进的粒子群算法进行迭代寻优.另外,在迭代寻优阶段,以计数器设置对搜寻结果进行监测,当过程陷入早熟时可以通过强制更换粒子,达到跳出局部最优的效果.
2.1基于动态马尔科夫覆盖简易发现方法的粒子群初始化过程基于CI测试与MI的动态马尔科夫覆盖简易发现方法分为2步.第一步从空图出发,进行连接边扩充:通过MI和MMI进行互信息排序,加入动态阈值α调节约束范围的大小,由于粒子数量通常较多,因此将动态阈值的运动步长设为0.01,则动态阈值为α=0.15i,i为粒子数,当节点间的互信息满足MI≥αMMI时,默认2个节点存在连接关系,添加无向边,直至完成对马尔科夫覆盖的候选节点进行初步限制.第二步对当前的约束环境进行收缩:在排除多余信息之后进行CI测试,在条件独立性断言成立时在马尔科夫覆盖中删除该节点,可以达到减少冗余计算,提高运算效率的效果.由于动态阈值的设定,将在不同阈值下得到不同的无向图结构,形成初始的无向图集群,之后再进行进一步的定向工作,使得无向图变为有向图.
基于动态约束模型的贝叶斯网络结构优化算法中构建马尔科夫覆盖约束部分的伪代码如下:

返回无向图集合G
将得到的无向图通过CRAE确定连接边的方向,假设Xi和Xj无向图中存在连接边的2个节点,则边的定向计算公式为
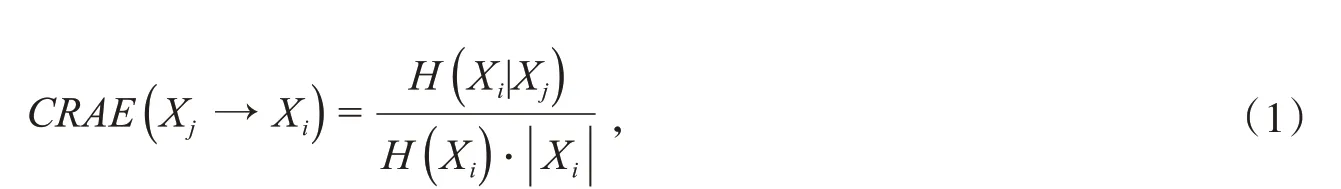
当CRAE(Xi→Xj)≥CRAE(Xj→Xi)时,连接边的方向应该为从节点i指向节点j.
由此,得到了初始粒子群,通过此方式不仅可以提高粒子的质量,同时也可以丰富粒子的多样性,得到复杂度各异的初始粒子,为后续的粒子群搜索过程提供帮助.
2.2适用于BN的小规模粒子群优化算法粒子群算法由鸟类觅食行为衍变而来,胡旺[25]等曾提出一种简化而得到的粒子群更新方式

其中,ωXt表示过去对现在的影响,其程度大小由ω调节,c1r1(Pbest-Xt)表示粒子的自我更新,c2r2(Gbest-Xt)表示粒子与群体之间的资源共享.在粒子群算法中最重要的是更新环节,即粒子速度和位置的更新.将每一个邻接矩阵所表示的有向无环图作为粒子位置,由于其二进制的特性,在粒子群更新公式中无法通过常规的调节系数对其进行操作,为保持粒子更新过程中有向无环图的原始意义,将通过对其进行加减边或反转边的操作形式决定粒子的变更程度,Pk表示在优化算法中每一个代表当前粒子的DAG结构.将更新过程改进后的粒子群算法应用于BN结构学习中,故而粒子群更新公式可以改写为
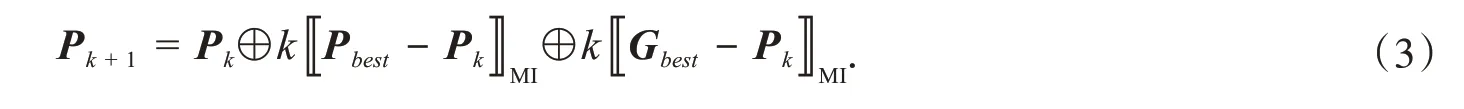
此处需要定义2个新的算子:
⊕定义为执行粒子加减边的更新操作;
〚〛MI定义为通过互信息对需要执行加减操作的边进行筛选.
对于每个操作的具体执行方法,将扩充为式(5)和(6)进行具体阐述.
首先运用BIC评分作为该更新算法的评分函数,计算当前结构的适应度优劣,该评分函数如下所示

BIC评分函数由2个部分组成,分别是度量候选结构与样本数据匹配程度的对数似然函数和与模型本身维数和数据集规模的相关罚项,这使得该评分可以有效平衡所得贝叶网络结构的匹配性与复杂性,有助于最终结构的搜寻.
因此,当BIC(P best)>BIC(P g)时,

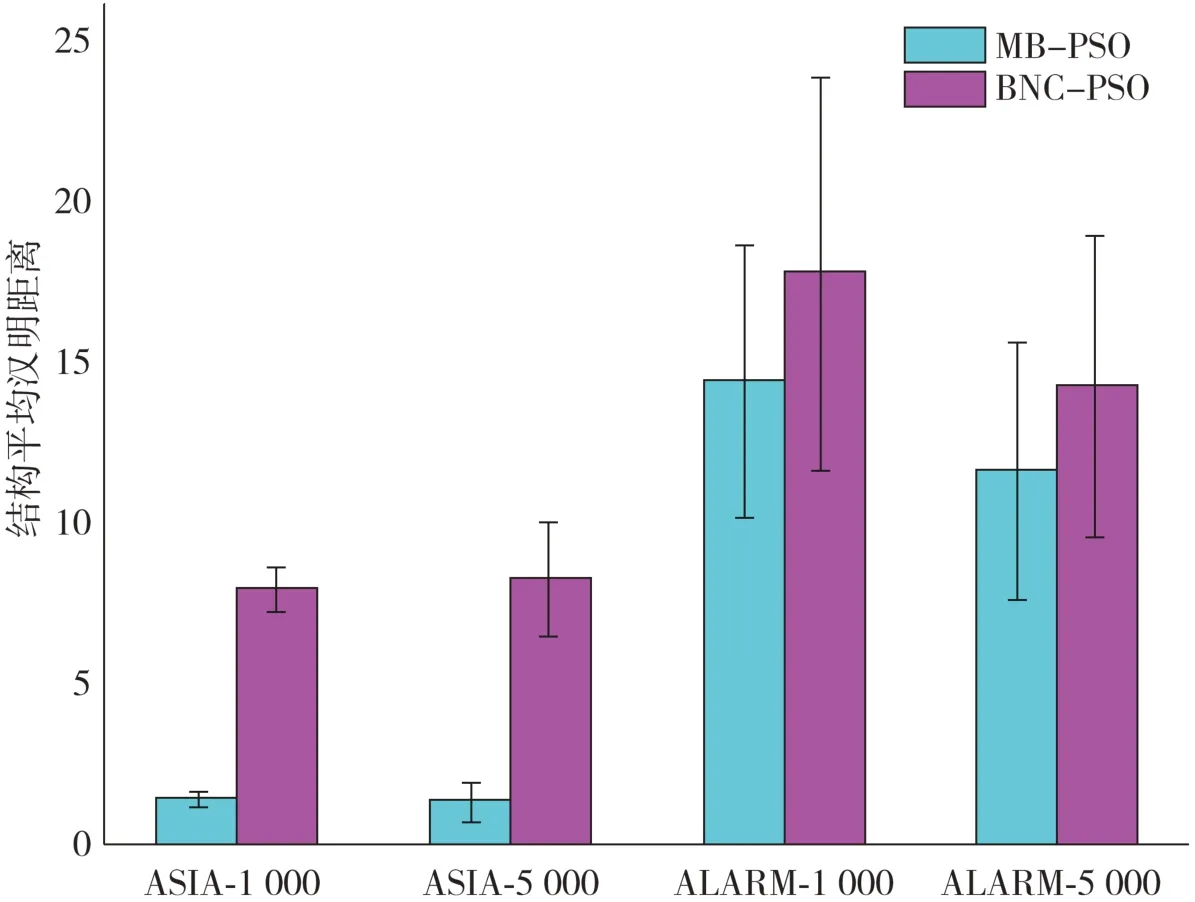
当BIC(P best)≤BIC(P g) 其中,C是对矩阵的复杂度计算,文中复杂度仅指网络结构中有向边的数量;()MImax和()MImin分别是将当代最优结构与当前结构相比,选择差异边中互信息最大(最小)的边,该操作也即当前结构评分较低时,根据与最优结构比较的复杂度高低分别适当增加(减少)当代最优结构中与当前结构相比不同的边中互信息最大(最小)的边,使得当前结构可以学习部分最优结构的节点关系,使其复杂度向当前较优结构靠拢. 特别的,当BIC(G best) 其中,turn代表对原有结构执行边的反转操作,Pg±rand(0,1)为在当前结构中做随机的加减边操作. 当前结构评分达到最佳时,在保存该结构数据的同时将通过随机的形式在结构中进行边的变换,增加粒子的多样性. 通过如图2所示的例子进行说明. 图2中MI(i,j)为节点i到j之间的互信息值.在该示例中,设BIC(P k) 图2 改进的粒子群优化算法更新示例 本文提出的更新方式不仅可以调节当前粒子不断向全局最优和当代最优靠近,还可以在一定程度上帮助搜索过程跳出局部最优. 2.3跳出局部最优的搜寻计数器和重启机制由于目前的搜索算法大多面对易陷入局部最优的特点,因此通过插入计数器,计算当前最优粒子的重复迭代次数.当最优值连续迭代3次及以上时默认陷入局部最优,进行粒子的强制更换,即删除当前评分值最低的粒子.在最优粒子的基础上进行反转边或者加减边的操作,并将该粒子替换当前评分值最低的粒子进入下一次迭代循环,其过程如图3所示. 图3中k是当前迭代次数,t是计数器的记次数,代表最优结果的重复次数.当最优结果经历3次更新不发生变化时,默认寻优更替发生了停滞,即在当前环境下难以找到更优解,故而为了寻找更优解,需要替换原有效果不佳的粒子,通过引入新粒子的方式增加更优结构出现的可能性.新粒子由当前的最优粒子通过随机加减边的方式产生.与此同时,还会通过检测各粒子结构中是否产生闭环,并加以排除. 图3 基于计数器的粒子替换机制 2.4算法实现具体步骤 步骤1设置空图,添加动态阈值α,当MI≥αMMI时添加无向边; 步骤2CI测试确定每个节点的马尔科夫覆盖,生成无向图组; 步骤3CRAE函数对无向图定向,生成初始粒子群; 步骤4计算当代粒子的BIC评分值与复杂度,记录当代粒子评分值,更新全局最优与个体最优; 步骤5选择相应的更新机制,进行边的加减反转操作; 步骤6计数器在迭代循环内判断收敛状态,替换质量较差的粒子; 步骤7重复步骤4、步骤5、步骤6,直至达到设定循环次数,跳出循环,得到最终解结构. 为了证实该算法的性能,选择了2个公信力比较强的网络生成4个数据集进行测试,分别是:AISA网络和ALARM网络.AISA网络是一个反应呼吸道疾病的医学例子,说明病人是否患有与胸部诊所有关的肺结核、肺癌或支气管炎,每个变量可以采取2个离散状态.分别利用1 000个案例的数据库和5 000个案例的数据库训练网络结构.ALARM网络是告警相关性和故障诊断模型,具有37个节点,同样通过1 000组数据和5 000组数据进行结构训练.与此同时与BNC-PSO[21],MMHC[9]和IK2vMB[6]3种方法在4个方面进行对比,分别是:最终BIC评分(ABB),以s为单位的平均运行时间(ART),得到最佳个体的平均迭代次数(AGB)和最佳个体与正确BN结构的平均汉明距离(AHD),并且在结果收敛的条件下使用相同的种群大小和迭代次数,分别是60和500. 实验平台:Intel Corei7⁃5300U,2.30 GHz,64位Windows10、8 GiBRAM内存.程序均用Matlab软件在R2014a版本下编译,并且均以BIC评分作为最终判定结构适应度的标准评分,每个实验重复50次并计算其平均值. 表1是实验网络的各项信息,包括实验网络名称、数据集、实验数据组数量、网络节点数、网络连接边数和正确网络结构在不同数据集下的BIC评分. 表1 数据集标准信息 4种算法中,BNC-PSO算法首先随机产生初始种群,运用BIC评分计算粒子的适应度值获得初始最优解,然后通过遗传算子更新粒子,并计算BIC评分,并对最优值进行更新,直至满足终止条件.MMHC则是在获得候选父节点集合之后运用贪婪爬山搜索算法,基于BDeu评分函数通过对结构边的加减的评分判定获得最终的最优解.IK2vMB算法是一种基于马尔科夫毯的改进K2算法,该方法分为2个部分:1)首先利用MI建立最大权重生成树,构建无向图,运用条件相对平均熵对该无向图的连接边进行定向,然后将该有向图分成节点块进行排序并修正,最后通过将所有节点块拼接获得初始结构;2)首先寻找根节点的马尔科夫毯,然后根据Koller-Sahami算法得到马尔科夫毯中的节点排序,最后运用修正得到节点序列代入K2算法学习到最终的BN结构. 在表2中可以看出,在通过马尔科夫覆盖对初始粒子群进行有目的的初始化之后,可以在更少的迭代次数下得到当前算法的最终结果,这一点反映了算法的运算效率相对更高.当网络结构规模较小的时候,该初始化方式并不会对运算速度造成严重的负担,但是却能对结构学习产生非常积极的作用.与BNCPSO相比,加入了计数器和粒子替换机制后的MB-PSO还可以在结果暂时收敛之后跳出局部最优,得到结果更佳的BN结构. 表2 不同算法在各数据集中的比较 从图4可以看出,算法在第五代左右经历了第一次收敛,但是在第十代再次获得新的结构,这也表明了计数器设置的必要性与其产生的跳出局部最优的效果.BNC-PSO和IK2vMB均面临学习结果的精度较低的问题,这与其更新方式和学习机制的设定有密不可分的关系,MMHC虽然能够保证相对较稳定的学习质量,但是依然会面临随着网络结构复杂度提高后贪婪算法迭代次数过多,不再适用的问题. 图4 MB-PSO算在AISA网络1 000组数据集下某次BIC评分前50代数据截取图 从表3和图5可以看出,虽然本文算法运行时间在网络规模扩大后失去了优势,但是依然能够确保其收敛速度和学习精度保持较高的水平,体现在本文算法的初始粒子群BIC评分较高以及最终结果的汉明距离标准差较小这一结果上,表明本文算法具有较高的稳定性.在保证稳定性与最终汉明距离结果均比较理想的情况下,无论是小规模的8节点网络,还是具备一定规模的37节点中型网络,通过本文算法得到的最终网络结构的精度都是可以保证的.因此,本文算法在中小规模的贝叶斯网络结构学习中可以得到较好的效果. 表3 ASIA网络和ALARM网络在1 000和5 000组数据集下的初始粒子平均BIC评分 图5 ASIA网络和ALARM网络在1 000和5 000组数据集下的平均汉明距离与标准差 综上所述,在中小规模节点的情况下,本文算法在运算时间和学习精度2个方面的优势比较明显,计数器和粒子重置机制也有效保证了结果的收敛效率,降低了陷入局部最优的可能,使得算法在保证结果质量的同时能够较快的实现收敛,这一结果为后续进行大规模网络结构学习提供了可能. 基于启发式群智能算法PSO和动态马尔科夫覆盖构造了一种混合结构学习算法,首先通过动态约束阈值构建基于马尔科夫覆盖的无向图集合,通过CRAE定向和MI约束边的生成条件添加新的有向边增加初始化粒子的多样性,构成多个联通的有向无环图作为PSO的初始粒子,然后运用PSO的思想重构粒子更新过程,以适应度和复杂度作为判断粒子优劣的条件,通过加边、减边、反转边的方式进行粒子更新,最后在PSO寻优过程中加入计数器和粒子更替机制,时刻监视粒子最优解的更新动态,做到优胜劣汰,及时以新粒子替代“劣质”的粒子,避免过早收敛陷入局部最优.实验结果表明,粒子的初始化过程使得初始粒子品质更佳,加快了粒子的寻优速度;PSO优化方法的重构使得BN结构学习合理的与粒子更新相结合,从而使学习得到的结果准确度更高;计数器作用下的粒子更替可以有效规避算法过早收敛陷入局部最优.在与其他算法的实验比较中,本文算法可以做到学习精度更高,效率更佳,可以进一步应用于复杂网络结构和解决实际问题中.
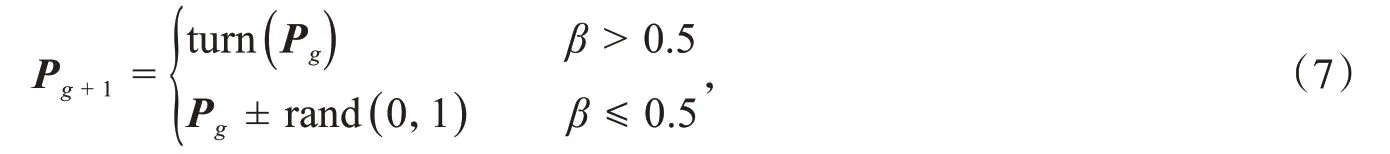


3 实验结果及数据分析




4 小 结

