动态三支决策研究综述及展望

王君宇 李言 李丽红

(1.华北理工大学理学院,河北唐山 063210;2.河北省数据科学与应用重点实验室,河北唐山 063210;3.唐山市工程计算重点实验室,河北唐山 063210)

0 引言

三支决策(Three-way Decisions,3WD)是姚一豫教授提出的一种分析和解决复杂决策问题的理论[1]。其主要思想是“三分而治”和“化繁为简”,将整体分为三个独立的部分,根据收集到的信息对不同的部分采用不同的处理策略[2]。

目前,基于时间和空间两个维度,三支决策的研究可以分为静态三支决策和动态三支决策。静态三支决策只进行一次三支决策;动态三支决策实施多阶段的三支决策,进而做出最终决策。结合实际决策背景,如何在动态决策信息系统下建立动态三支决策模型,提高决策效率、降低决策代价是当前的热点问题。学者们提出了序贯三支决策[3]、多粒度三支决策[4]、多分类三支决策[5]等动态三支决策模型。

在实际决策时,人们往往会随着所获信息的更替而不断改变决策方案。尤其是在大数据时代,人们需要在尽可能短的时间内快速决策。因此,系统地研究动态三支决策的理论、模型和应用有重要的意义。本文对动态三支决策的基本理论、研究现状和相关应用进行综述,总结和展望其未来研究方向。

1 三支决策基本理论

作为二支决策的拓展,三支决策考虑到不确定因素,引入了延迟决策。经典三支决策模型[6]是基于贝叶斯理论进行的决策,具体描述如下:

设状态空间 Θ= {X,﹁X}表示对象x的两种不同状态,动作集合A={aP,a B,aN}表示对x进行决策采取的三种不同行为,aP,aB,aN分别表示对象x属于、不一定属于和不属于集合X的行为。决策时相应的损失代价函数如表1所示。

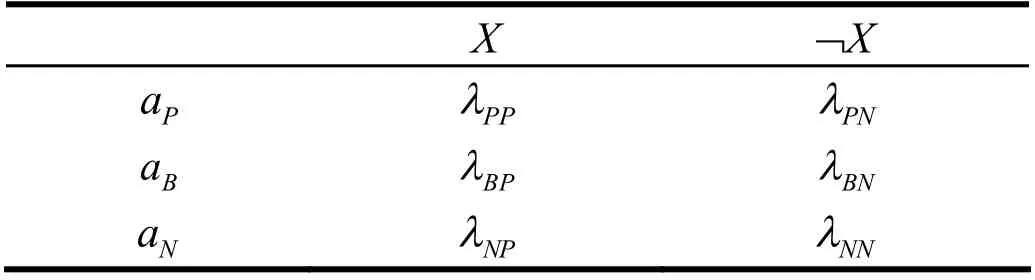
表1 损失代价函数Tab.l Loss cost function

其中,λPP,λBP,λNP分别表示x属于X而采取行为aP,aB,aN时的损失,λPN,λBN,λNN分别表示x不属于X而采取行为aP,aB,aN时的损失。Pr(X|[x])是条件概率,对于x来说,采取一个决策行为时的期望代价为:

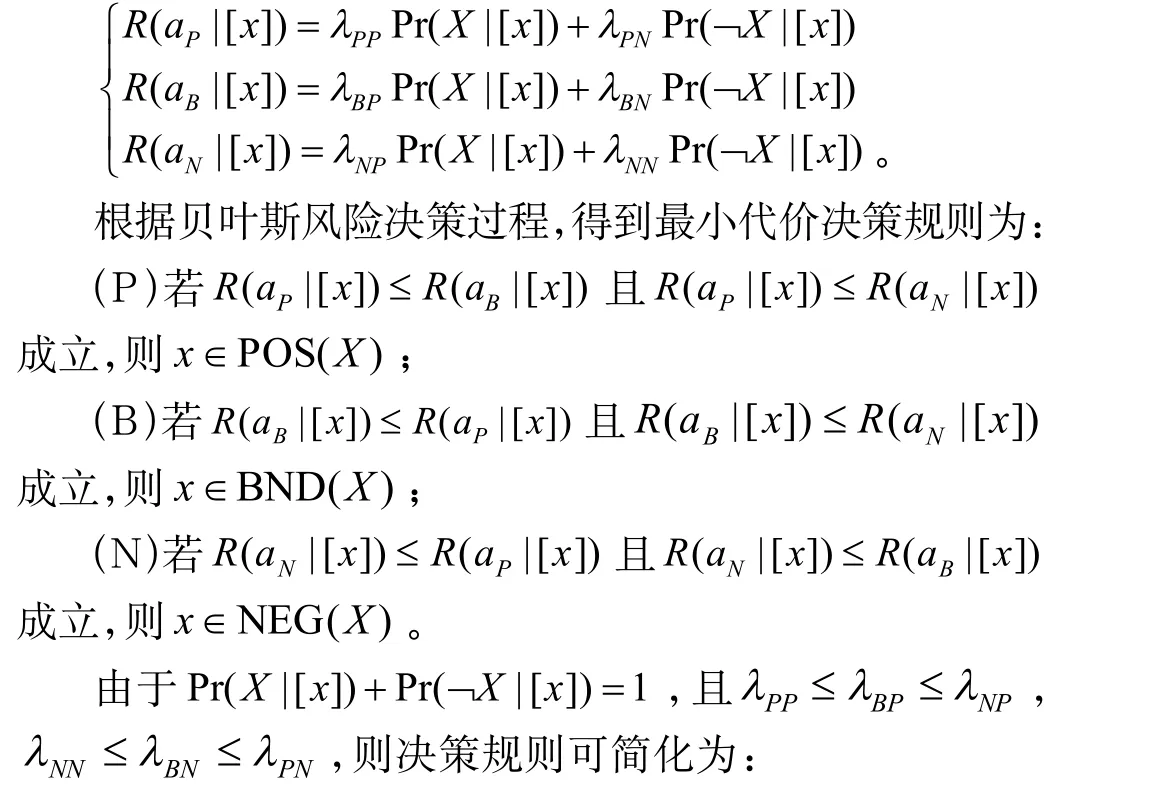
2 动态三支决策的发展

2.1 动态三支决策

在现今信息更新瞬息万变的时代,传统的三支决策在复杂动态的信息系统下更加高效准确地做出决策存在局限,学者们提出并发展了动态三支决策理论,实现了实时高效的信息处理和决策分析。动态三支决策是由多次决策组成的,其过程如图1所示。

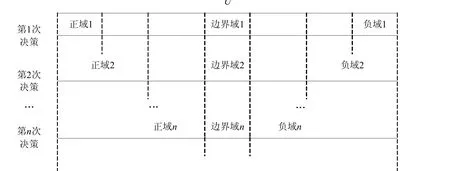
图1 动态三支决策Fig.1 Dynamic three-way decisions

在动态三支决策过程中,动态决策的情况大致可分为五类:第一,对象的增添和删除;第二,属性的增加和减少;第三,条件属性值或决策属性值的更新和修改;第四,决策损失函数的改变;第五,多粒度的更新。通过动态决策过程对阈值的影响,对三个域进行重新划分,进而做出最终决策。

2.2 动态三支决策研究现状

在动态决策信息系统中,对象的增添和删除可以提高决策的效率。张春英等[7]根据对象单向迁入和单向迁出的规律给出了相应算法,设计了对象双向迁入和迁出的动态算法,提出了一种基于P S-粗糙集的动态三支决策算法,最终提高了决策效率。

动态变化的数据会使信息系统不断更新,原有决策信息系统的信息结构和特点随之改变,属性的增加和减少可以提高决策的准确性。李艳等[8]提出了一种优势-等价关系下基于序贯三支决策的约简更新方法。该方法将多粒度结合起来形成动态粒序,当对象集和属性集变化时,通过重用原有信息快速更新属性约简,从而降低知识更新的代价。

在决策过程中,知识内涵能具体刻画对象的属性值,它使得对象可以参与计算、规则制定,从而进行决策。条件属性值或决策属性值的更新和修改能建立相适应的决策模型。张清华等[9-10]针对数值型属性定义了属性比率,并利用其来描述对象,解决了给定接受域对象数时,通过属性值更新实现动态三支决策的问题。根据字符型属性对象间的优异程度,给出了对象的动态特征的提取方法,建立了动态三支决策模型,该模型同样可以处理数值型属性的对象,且减少了决策的更新成本。

损失函数可以确定动态三支决策模型的阈值参数,多数情况下是人为给定,决策损失函数的改变可以降低决策代价。Liu等[11]针对不完整信息系统中出现的缺失值,利用区间数获取损失函数,将不完整信息表和损失函数表结合在一起,用于处理新型的三支决策模型。

序贯三支决策是一种典型的动态三支决策模型,最早由Yao提出[3]。经典的序贯三支决策模型构建一个多层次的粒结构,自上而下,粒度由粗变细。在某一粒层进行三支决策,再把这一层的边界域作为下一层的处理对象,直至边界域的对象被逐渐划分到正域和负域。实际上,随着信息的变化,针对不同的任务和目标,不同的粒度划分和区域组合都有可能影响最终的决策结果。

在动态三支决策过程中,对象的增添和删除、属性的增加和减少反映了决策的时间动态性,而在多粒度空间下决策的过程和粒度的优化反映了决策的空间动态性。三支决策的时间性和空间性不可分割、相辅相成,同时动态决策过程更强调决策过程和结果代价,因此学者们致力于研究对象、属性、条件属性值或决策属性值、决策损失函数以及多粒度等因素的变化,以降低决策时间、减少决策成本和提高决策质量。

在理论研究方面,动态三支决策主要应用于优化属性约简方法、代价敏感问题以及动态决策信息系统下的最优选择问题等,还可用于分类、聚类、规则学习等数据分析模型。在实际应用方面,动态三支决策的理论和模型等研究成果被广泛应用到医疗诊断、图像识别、邮件过滤和风险决策等领域。

3 动态三支决策的展望

目前人类已经进入到一个信息技术高速发展的大数据和人工智能时代,如何存储、处理和分析数据,是现今研究的重点问题。在处理动态数据、分析问题、进行决策时,现有动态三支决策大多是运用分别决策的策略,通过多分类、多粒度或序贯的思想进行决策。今后,动态三支决策有望借助区块链等技术存储信息,进行整体决策。此外,可拓学能将事物形式化地展现出来,与可拓学等理论结合,建立更具应用意义的形式化模型,可拓展动态三支决策的应用领域。

在动态三支决策中,损失函数多数情况下是人为给定,对于评价函数的选取也掺杂许多人为因素,所以寻找最优阈值设置的新算法很重要。在面向多类数据和动态数据时,未考虑动态决策和规则冲突问题,规则获取过程需要进一步完善。因此,在处理如多类和混合等复杂动态数据时,运用贝叶斯理论、优化算法等寻找最优阈值设置,基于区块链的链式数据结构思想获取新的决策规则,建立能够进行整体决策的数学模型,拓展决策模型的相关应用,需要进一步研究。

4 结论

三支决策作为一种能有效处理不精确和不确定性信息的决策工具,具有非常强的普适性和应用性,尤其是动态三支决策在各领域的作用正得到研究者们的逐步重视。本文对动态三支决策做了综述性分析,在动态决策信息系统下,将对象、属性、条件属性值或决策属性值、决策损失函数以及多粒度等进行单一变化或者多个变化,能有效提高决策的准确性、降低决策成本。利用动态三支决策处理信息,建立更具应用意义的决策模型,可作为今后研究的方向。