利用Lyapunov 函数确定粒子群算法参数选择*
朱辰晨 贾群
(淮南师范学院机械与电气工程学院,安徽淮南 232038)
0 序言
粒子群是一种基于空间多维搜索的随机智能算法,它是由Kennedy和Eberhart在1995年提出,其算法模型相对简单易于实现。粒子群在寻优过程中既能够体现出群体的智能,又依赖于种群的每一个成员即粒子之间的协同合作寻测全局最优点。但PSO基本模型本身还有许多不足之处,比如算法易早熟、易陷入局部最优等。为了解决基本PSO算法存在缺陷及提高算法本身的适用性,很多文献提出采用其他智能算法,如小波、神经网络、混沌、遗传、量子、聚类分析、模糊理论等进行一定的改善。但究其PSO算法模型本身而言,任何改进最终都会体现在算法参数的选择上。1998年Shi和Eberhart引入惯性权重系数w并验证了w选取不同范围对标准PSO算法性能的影响;2000年Eberhart和Shi又在PSO迭代方程中引入压缩因子对粒子的速度和位置进行约束,从而进一步提高了算法的性能[1-4]。
本文更侧重参数之间的关系,在分析PSO基本算法的基础上,运用控制理论中关于稳定性分析的李雅普诺夫函数从粒子运动稳定性角度对PSO算法进行分析,得到参数之间的约束关系,以此作为确定PSO算法参数选择的基本依据,并通过相关的典型函数进行测试,充分证明了选择合适的参数约束关系对于提高PSO的稳定性收敛性具有非常重要的意义。
1 李雅普诺夫稳定性分析
1.1 PSO稳定性分析及相关定理分析
P SO算法本身是一种非常有效的群智算法,粒子在特定空间搜索过程中粒子通过不断调整自身最优位置和速度,同时兼顾全局最优位置变化,逐步地积聚于全局最优点,到达可行搜索域中的最优位置。粒子的运动具有逐渐趋向收敛、趋向稳定的特点。这一过程完全可以用Lyapunov原理来分析,许多文献都有较多的讨论,同时也有较深入的应用。根据Lyapunov原理对标准粒子群算法进行稳定性分析,在此基础上提出粒子群参数选择范围的基本依据。

根据以上分析,利用以下定义和定理[5]:

控制系统在平衡状态附近为渐近稳定,则Ω必须是正定的。判定Ω为正定的矩阵可以依据Sylvester准则,即判定矩阵正定的充要条件是该矩阵的各顺序主子式均G为正值。根据上述条件分析必须保证为正定,进一步可以确保Ω是正定的[5]。


1.2 计算分析和PSO算法参数确定

式(3)的第一项为粒子先前的速度,联系粒子当前的状态,是粒子惯性的表现,起到了平衡全局和局部搜索的能力;第二项反映了粒子对“自身经验”的认识,即粒子自身记忆对搜索的影响,这一项使粒子具有全局搜索能力,避免陷入局部最小;第三项反映了整个种群的“社会经验”,综合考虑了历次迭代过程中整个种群所获得的“经验”,表示粒子间的信息共享与相互合作,有利于粒子全局搜索能力的提升[2-4]。

引入和选取中间状态变量φ(t) ,并根据系统的空间状态方程求解,选择状态变量得到以下关系:


可以确定ξ的取值范围是:ξ∈(ω+ 1,2ω+2)
图1是结合上面的推导分析所得到的ξ和ω取值关系图。红色和黄色区域是Frans van den Bergh通过代数推导方法所得到的PSO算法的收敛区域,黑色区域为算法的不收敛区域,粒子在此区域飞行过程中完全发散。红色的区域为本文通过Lyapunov Function进行稳定性分析所确定的ξ和ω的取值范围,这一范围能够保证粒子在空间搜索过程中达到稳定收敛的效果。

图1 ξ和ω取值关系图Fig.1 ξ and ω value relationship diagram
2 PSO算法的改进和仿真分析
2.1 PSO算法的改进
基于以上分析对标准PSO算法可以进行参数约束的算法改进(简称Constraint PSO),其中
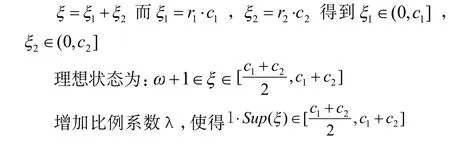
保证参数落在红色区域中,使粒子飞行速度和位置在每一次迭代过程中有一定的变化,这将有利于算法克服局部最优的缺陷。进而对于整个系统而言,既能兼顾PSO算法的随机性,同时又能够在一定程度上保证粒子在空间运动中的稳定性进一步保证了算法的收敛性。
2.2 函数测试及仿真
仿真条件:这里选取24个粒子,空间维数设定为3维,采用多峰函数进行测试分析。
f是Rastrigrin函数,该函数是个多峰值的函数,约有10n个局部极小点,而且此函数是一种典型的非线性多模态函数,峰形呈现高低起伏的形态,具有不定跳跃性的特点,所以不易查找到全局最优值。

图2中可以看到多峰函数f是具有多峰特征,由于在搜索域中存在较多的峰值,相对于单峰函数,PSO在搜寻全局最优点的时候更容易陷入局部最优。图3是标准PSO和constraint PSO的粒子绝对位置的对数值变化过程,可以看到Constraint PSO收敛性在多峰且复杂情况下能够具有较好的收敛性。图5表明Constraint PSO的粒子在空间迭代过程中聚集程度较好,而图4距离中心处有较多的散点。通过两个图的对比分析,说明基于Lyapunov函数的PSO算法的粒子在空间寻优过程中能够有效地聚集在收敛点处且收敛性较好。

图2 f 函数空间效果图Fig.2 f function space effect diagram

图3 粒子绝对位置的对数值变化过程Fig.3 The logarithmic change process of the absolute position of the particle

图4 标准PSO 粒子聚集程度Fig.4 Standard PSO particle aggregation degree

图5 Constraint PSO 粒子空间聚集程度Fig.5 Constraint PSO particle spatial aggregation degree
3 结论
通过以上分析,可以清楚地发现依据Lyapunov函数所确定的PSO参数关系即ω+1<ξ<2·(ω+1),对于算法的收敛性具有重要的影响。采用基于Lyapunov函数的稳定性分析所确定的PSO参数选择关系可以有效保证算法具有较好的收敛性。具有参数约束的PSO算法(Constraint PSO)能够使每一个粒子飞行于较好的区域、更易于收敛,同时有效地提高粒子飞行的稳定性,使算法本身更具有较强的鲁棒性。

