W 型磁极结构永磁同步电机振动特性分析
王涛,赵海宁,于慎波
(沈阳工业大学机械工程学院,辽宁 沈阳 110870)
近年来,随着人们对于能源和环境问题的担忧,越来越多的学者开始关注新能源行业的发展.电机作为新能源蓬勃发展不可或缺的一部分,承担着能量从产生,转换、输送等环节最为重要的一部分,应用于各行各业,直接或间接的影响着人们的生活的方方面面.永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)作为一种特殊的电机,具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高等显著优点,因此PMSM已经在民用、航天和军事等领域得到了广泛应用[1].但如何使电机运行更加平稳,产生的振动更低,一直是困扰国内外学者的问题.
国内外学者对于电机振动方面的研究已经相对比较成熟,研究路线通常从电机振动的产生机理出发,通过更改电机定子、转子或者永磁体结构达到减少电机振动的目的.沈阳工业大学于慎波教授在论文中比较全面详细地分析了永磁同步电机产生振动的原因,计算了气隙径向电磁力并对其进行傅里叶分解,对谐波进行分析,用数值方法找到了产生径向电磁力谐波的规律,研究了谐波次数对于电机振动的影响[2].安徽理工大学学者提出了基于逆系统解耦综合滑模控制系统的方法, 通过对电机转速等多参数统一控制从而降低永磁同步电机振动[3].文献[4]基于能量法利用数值分析法,通过微分方程对转子气隙磁场进行解析计算,并在空载情况下分析了不同阶数的激振力波幅值与偏心率的变化情况,结果发现转子偏心不仅会对电磁转矩产生很大影响,而且会产生低阶数的激振力波源,从而增大了电机的振动.文献[5]通过粒子群算法寻找最优的电机极弧系数,对电机大小磁极结构进行不同配制,从而降低了对转矩脉动幅值影响较大的气隙电磁力谐波阶次,进而降低电机的振动.文献[6]提出了一种能预测和优化PMSM的新方法,将建立电磁元件与机械振动声学联系起来,得到了电压和电流谐波的解析表达式,建立相应的径向电磁力分析,确定了声振模式,最后以一台样机进行试验表明这种方法可以有效预测电机的振动.文献[7]中提出了一种混合随机开关频率- 死区补偿技术,通过降低逆变器电流谐波从而抑制电机振动.
内置式W 型永磁同步电机具有高功率密度因数和持续稳定的高转矩输出等优点,W 型转子磁路有着可提供充足的用磁量、每极磁通较大、空载系数较小等优点,但内置式W 型转子磁路相对普通电机转子磁路更加复杂,所以对内置式W 型转子磁极结构进行深入研究有较强的现实意义.永磁同步电机的振动主要由自身的电磁振动引起,其中电磁振动又分为径向振动和切向振动,他们分别由径向电磁力和切向电磁力的波动产生.
本文将利用有限元软件对W 型磁极结构永磁同步电机进行分析,探究影响电机振动主要因素.
1 永磁同步电机气隙磁场分析
1.1 永磁同步电机二维模型建立
电机转子上的永磁体与电机通入正弦的电枢电流共同作用形成电机的气隙磁场,电机的气隙磁场中的振动源主要有电磁力、以及气隙磁导和合成磁动势相互作用产生的能量波动引起的齿槽转矩,影响电机的平稳运转.首先利用有限元软件Ansoft 对永磁同步电机进行二维磁场建模仿真分析,得到电机的磁场分布图、磁通密度云图以及气隙磁密随时间空间变化的曲线图,然后在气隙磁场中分别提取径向和切向的电磁力密度,通过Matelab 编程计算出径向和切向的电磁力并使对其进行傅里叶分解得到电磁力密度的谐波分析和频谱分析,得到电机径向电磁力频谱分析.
本文以一台4 级60 槽,额定转速为1 500 r/min 的内置式W 型永磁同步电机为研究对象,永磁同步电机物理模型见图1,详细参数见表1,根据电机的几何参数利用Ansoft 软件建立电机二维有限元分析模型见图2.

表1 内置式W 型永磁同步电机主要参数Tab. 1 Main parameters of internal W- type permanent magnet synchronous motor

图1 电机物理几何模型 Fig. 1 Physical geometry model of motor

图2 二维有限元仿真模型Fig. 2 Two-dimensional finite element simulation model
1.2 永磁同步电机气隙磁场仿真结果分析
在气隙中画圆设置采样点,编写求解气隙磁密以及电磁力的公式,导入到Ansoft 进行后处理分析,得到随空间位置变化的径向气隙磁密和切向气隙磁密,见图3 和图4.由于电机定子槽数比较多,电机径向气隙磁密在电机内部每一个定子槽处波动比较大,这是因为定子的齿槽效应引起的.径向气隙磁密整体波形接近正弦波呈周期性变化.

图3 随空间位置变化的径向磁密Fig. 3 Radial magnetic density varying with spatial position

图4 随空间位置变化的切向磁密Fig. 4 Tangential magnetic density varying with spatial position
谐波分析是电机气隙磁场分析最为重要的一部分,谐波对于电机危害极大,谐波可以增加电机损耗,降低电机工作效率.因此需要对电机的气隙磁密进行谐波分析.在Ansoft 中导出电机的径向和切向气隙磁密数据,使用Matlab 对导出的气隙磁密数据运用傅里叶函数进行分解,进而得到气隙磁密的谐波分析图,见图5 和图6.分析得出径向磁密谐波基波峰值为0.96 T,切向磁密谐波峰值为0.048 T,由此径向谐波的幅值远大于切向的谐波幅值且谐波的含量较少,这也验证了电机径向磁密产生的电磁力是电机发生电磁振动主要原因.径向谐波除了基波,其他各次谐波幅值都很小,由切向磁密谐波分析图发现谐波占比较大,尤其2 次、6 次、10 次谐波的幅值偏高,对于电机齿槽转矩的影响比较大,从而影响电机的平稳运行.综上径向电磁力低阶次的谐波是电机电磁振动的主要激振源.

图5 径向磁密谐波分析Fig. 5 Radial magnetic density harmonic analysis

图6 切向磁密谐波分析Fig. 6 Tangential magnetic density harmonic analysis
电机中的电能和机械能主要通过电磁力进行转化的,求解电机的电磁力是分析电机振动的基础.由机械动力学知识,当电机电磁力频率与电机的固有频率相近时会引起共振,从而加剧电机的振动,因此对电磁力的求解以及对电磁力密度的谐波分析尤为重要.通过有限元分析随位置变化的径向电磁力密度见图7.永磁同步电机运行时气隙的基波磁场和谐波磁场相互作用产生有用输出转矩的电磁力,同时也伴随产生各个阶次以及各种频率的径向电磁力波.再次将有限元分析的数据导入到Matlab 中,对其进行傅里叶分解得到电磁密度随空间位置变化的谐波分析图,见图8.由图8 可知电机气隙磁场中谐波占比很高,正弦形畸变率大,容易引起电机的共振,会产生较大电磁振动.产生的电磁力波中随着磁场谐波次数增大,其对应的谐波磁场幅值逐渐变小,不会产生较大的电磁振动.
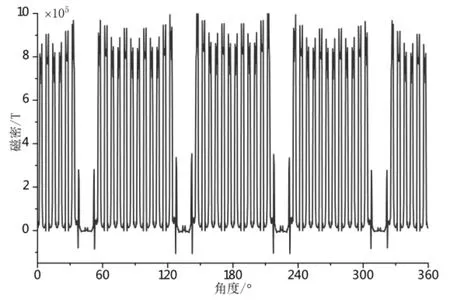
图7 随角度变化的径向电磁力密度图Fig. 7 Radial electromagnetic force density map with angle variation

图8 径向电磁力密度谐波分析图Fig. 8 Harmonic analysis of radial electromagnetic force density
为了确定电机径向电磁力波的频率是否与电机的固有模态频率接近,需要对径向电磁立波的频率进行计算,通过f=2pf0计算的电机径向电磁力波频率见表2.

表2 激振电磁力频率Tab. 2 Excitation electromagnetic force frequency
由表2 可知,除了基波频率外,400 Hz 所对应的径向电磁力的谐波幅值最大,因此400 Hz 是径向激振力谐波中对电磁振动影响比较大的电磁力频率.
2 永磁同步电机模态分析
模态分析主要应用在工程振动领域,是用来研究机械结构振动特性一种分析方法,机械结构的振动特性包括固有频率和振型,机械结构的固有频率和振型只与自身的材料属性以及结构形状有关,与外界的施加的载荷无关.机械结构的模态分析是非常基础的动力学分析,其他动力学分析都需要在模态分析的基础上进行.模态分析可以确定结构的固有频率以及振型,可以知道结构物体在某频率范围内的各阶模态的振型特性,可以协助预测在不同载荷作用下结构的振动形式,模态分析也可以确定自身结构的自振周期.通过模态分析,可以改变结构物体的形状设使之避开某有害的频率段以某种特定的频率振动,还可以分析同一结构对不同施加下载荷是如何响应的进行.对电机结构进行模态分析是研究电机振动非常关键的一步,使用模态对电机振动进行研究时,电机的模态分析只与电机自身的物理结构有关,与外界的激励无关,即只与电机结构自身的材料密度、弹性模量以及泊松比有关[8].
为了防止电机的固有频率与电机径向电磁力的频率接近发生共振,加剧电机的抖动,因此需要对电机进行模态分析.
在对电机进行模态分析时,可将电机看作一个多自由度系统,其振动运动方程为[9]
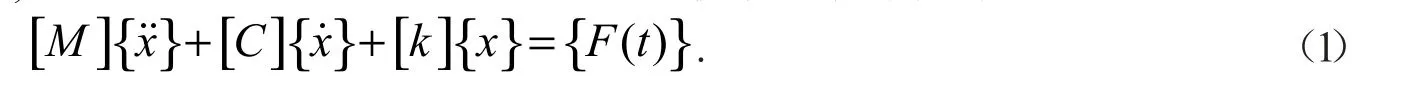
式(1)中:[M]为系统质量矩阵;[C]为系统阻尼矩阵;[K]为系统刚度矩阵.
在电机的结构确定后,整个电机系统质量和刚度矩阵就已经确定,由经典的特征值问题得知,系统的阻尼矩阵为零,因此电机系统的运动方程为

将电机的振动可作自由振动的简谐运动处理,其位移变化视为正弦变化

将式(3)式(2)得

以上方程的求解是经典的求矩阵特征值的问题,设为该方程的特征值,那么ωi为机械系统的自振圆频率.特征值对应的特征向量为自振频率对应的振型.
2.1 电机模态分析
Workbench 建立该电机实体3D 模型,设置模态分析材料属性,参数见表3,对其进行模态分析.

表3 定子模态分析材料属性参数设置Tab. 3 Material property parameter settings of stator modal analysis
2.2 定子模态结果分析
电机模态分析结果见图9,电机各阶模态的频率见表4.二阶模态的固有频率就已达793.75 Hz,对照电磁力频率的频率发现,电磁力主要的激振频率与电机模态固有频率不接近,因此不发生共振.

图9 电机前5 阶模态振型Fig. 9 The first five modes of motor

表4 各阶模态频率表Tab. 4 Modal frequency table of each order
3 永磁同步电机谐响应分析
谐响应分析是一种分析线性动力学系统稳态响应的数值分析技术.在动力学中,当系统到持续的周期性的载荷时这种载荷将对系统的结构产生持续的响应,对这种载荷通过谐响应分析,可以用频率和幅值来描述这种响应.谐响应分析就是通过扫频分析,可以求取系统在简谐载荷下的位移,速度,加速度曲线,从这些曲线可以知道看到对应的峰值响应,分析可以得到峰值频率所对应的位移,速度以及加速度响应,通过确定系统结构在不同频率和幅值载荷作用下的响应,进而判断一个系统是否能够各种不同频率载荷下稳定运行[9-11].
为进一步探究W 型磁极结构永磁同步电机振动特性,需要对电机进行谐响应分析.将二维电磁场的定子齿单独切出,再次进行有限元计算仿真,将求解的电磁力映射在三维的电机定子齿上,见图10 和图11.分析电机在2 800 Hz 出位移加速度达到峰值,可能是电机气隙磁场高阶次的谐波与电机机壳定子频率比较接近,因此在电机设计中避免高阶次的谐波,或者通过改变电机机壳使电机在自由振动下的频率避开电磁力的频率.

图10 定子齿表面电磁转矩分布图Fig. 10 Electromagnetic torque distribution of stator tooth surface

图11 定子齿表面电磁力分布图Fig.11 Electromagnetic force distribution on stator tooth surface
对电机进行谐响应分析,得到机壳表面在电磁力的作用下的振动位移变化见图12,速度变化见图13,加速度变化见图14.

图12 机壳表面位移曲线Fig. 12 Surface displacement curve of casing

图13 机壳表面速度曲线Fig. 13 Surface velocity curve of casing

图14 机壳表面加速度曲线Fig. 14 Shell surface acceleration curve
4 小结
本文采用有限元法对电机气隙磁场进行了仿真计算,并对磁场仿真结果做了详细的分析;通过对电机径向和切向磁密谐波分析发现,电机的电磁振动主要由气隙磁场产生的径向电磁力导致的,并计算出幅值较大的低次谐波所对应的电磁力频率.为了防止与电机径向电磁力的频率接近发生共振,加剧电机的抖动产生振动,最后利用Workbench 软件建立该电机实体3D 模型,对电机的振动特性进行分析研究,求取了电机的各个阶次的固有频率和振型,并将电机的径向电磁力频率与电各阶固有频率进行了对比,确定了电机的电磁力频率与电机自身机械结构不发生共振.

