改进的密集连接网络遥感图像超分辨重建①

柏宇阳 朱福珍 巫 红

(黑龙江大学电子工程学院 哈尔滨150080)

0 引言

遥感图像分辨率是判定遥感图像质量的重要指标之一,高分辨率的遥感图像可反映出更多的地面细节信息。图像超分辨重建(super-resolution reconstruction,SRR)是一种利用单帧或多帧的低分辨率图像(low resolution,LR)通过专用的算法,在不改变成像硬件设备条件的情况下,生成较清楚的高分辨率图像(high resolution,HR)的技术,它使重建后的高分辨率图像的视觉效果远远超过参与重建的低分辨率图像。

图像超分辨算法总体上可分为基于重构的超分辨[1-5]和基于学习的超分辨[6-13]两大类。基于学习的超分辨算法相比于基于重构的超分辨算法在视觉效果上更好,因为此方法直接学习了低分辨率图像与高分辨率图像之间的映射关系。常见的基于学习的超分辨率算法包括基于样本的方法、基于邻域嵌入的方法、基于稀疏表示的方法和基于卷积神经网络的方法。本文研究的方法属于使用基于学习超分辨率算法。基于学习的超分辨算法是2002 年Freeman 等人[14]提出的,该算法中高分辨率图像块和低分辨率图像块的关系可通过机器学习实现,他们将此映射关系应用于马尔科夫网络,并利用贝叶斯置信传播理论来进行超分辨率重建。随后,在2004年,Chang 等人[15]将局部线性嵌入引入到超分辨率重建方法中,提出一种基于邻域嵌入的超分辨率重建算法。在2010 年,Yang 等人[16]认为图像具有稀疏性,因此将稀疏表示应用到图像超分辨中。

卷积神经网络在20 世纪80 到90 年代间出现,但在最近几年中得到了广泛的应用。卷积神经网络图像超分辨的基本思路是通过给定的训练集,其中包括低分辨率图像和高分辨率图像,将低分辨率图像作为网络的输入,网络的输出即为高分辨率图像。卷积神经网络的图像超分辨中最具有代表性的是超分辨卷积神经网络(super-resolution convolutional neural network,SRCNN)算法[17]与快速超分辨卷积神经网络(accelerating the super-resolution convolutional neural network,FSRCNN)算法[18],其中SRCNN 是基于卷积神经网络的图像超分辨的首作,其通过构建3 层卷积层来学习LR-HR 的映射关系。后来人们发现卷积网络深度越深,网络可以拟合出的函数越准确,结果也越好。但是随着网络越来越深,网络训练出现了梯度消失现象,也导致网络训练时难收敛的问题。He 等人[19]在2016 年提出了残差卷积神经网络(residual network,ResNet)解决了此问题,网络泛化性能也得到了提升。Kim 等人[20]提出了深度超分辨(very deep super-resolution,VDSR)算法,该算法将残差网络用在了图像超分辨问题上,也解决了超分辨网络较深时训练难收敛的问题。最近研究表明,如果卷积网络包含接近输入的层和接近输出的层之间的较短连接,则网络可以更深入、精确、有效地进行训练。密集连接网络[21](densely connected network,DenseNet)就是这样减轻了梯度消失的问题,也加强了特征的传递。其算法与残差网络相似,残差网络是若干个残差块进行级联,每个残差块由若干层组成,每一层的输出都是由本层特征与前一层特征之和。而DenseNet 是由若干个密集块级联,每个密集块由若干个层组成,但每一层的输出都是由本层特征与前面所有层的特征之和。由于有更多的短连接,DenseNet 算法的效果也比残差网络要好一些。

1 改进的密集连接神经网络

1.1 遥感图像退化模型

本文的超分辨网络针对的是遥感图像,遥感图像退化模型如图1 所示。

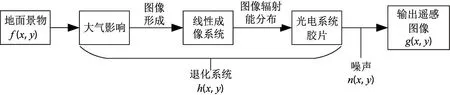
图1 遥感图像退化模型

地面景物图像受到大气影响、遥感成像系统、运动模糊、噪声等退化因素的综合作用,形成实际获取的降质遥感图像。遥感图像的退化系统h(x,y) 较复杂,地面景物通过大气后,形成了大气退化图像,再由线性成像系统,通过图像辐射能分布情况形成退化图像,其数学模型为

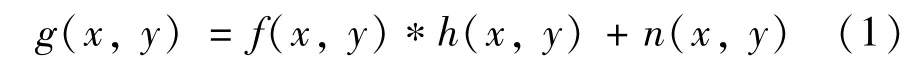
式中,f(x,y) 是高分辨率场景图像,h(x,y) 是遥感退化系统,n(x,y) 是噪声,g(x,y) 是实际获取的遥感图像,“*”代表卷积运算。

1.2 网络结构的改进

目前的VDSR 和DenseNet 超分辨网络都选用了91-images 或291-images 常规自然景物的彩色图像作为数据集,这些图像并不包含任何遥感图像。遥感图像的退化系统与常规彩色图像不同,且遥感图像包含了大量的土地、林地、湿地等各种的地面,这些图像的纹理和高频细节信息等,也与91-images或291-images 彩色图像存在一些差异,导致现有算法对遥感图像的超分辨效果一般。本文将训练测试样本改为遥感图像,在VDSR 网络的基础上,结合了密集连接网络,对网络进行了优化。并在网络结构、激活函数、学习规则等方面进行了改进,使其客观参数与主观视觉上都好于其他的算法。本文算法流程分为训练集的构造、超分辨模型训练和测试过程三部分。

由于当网络结构较深时,网络层拥有越大的感受野,效果就越好,深层网络在训练时较困难,而密集连接网络在层数较深时也容易收敛,本文算法仍使用密集连接网络。改进的网络结构如图2 所示,网络中将所有的残差部分更换为密集部分,同时为了扩展网络深度构建了两组密集连接部分,如图中虚线所示。输入为低分辨率图像,通过一个卷积层部分,输出一个低分辨率特征图。然后将此特征图通向了密集部分A,此部分包括了8 个密集块(A1～A8),再之后连接着瓶颈层A,这个层是将密集部分A中的密集块A1～A8 的输出进行特征叠加。

图2 改进网络的结构

瓶颈层A的表达式为

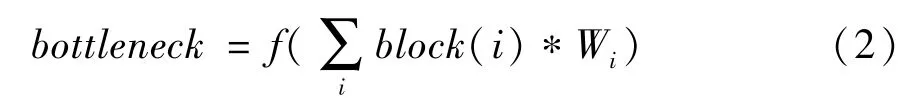
式中,bottleneck为瓶颈层A的输出,block(i) 为密集块的输出,Wi为第i块对应的卷积核,“*”代表卷积运算,f(·) 为激活函数。

之后是密集部分B,也由8 个密集块组成(B1～B8),再之后再通过瓶颈层B,这个层是将密集部分B中的密集块B1～B8 的输出进行特征叠加。叠加后的特征图通过反卷积层增加图像尺寸放大图像,最后经过重建层得到输出图像高分辨率图像,重建层也是一个卷积层。

网络包含两组密集部分,分别为密集部分A和密集部分B。每部分都是由8 个密集块组成,每个密集块也都含有8 个卷积层,且这8 个卷积层的每个层都与其前面的所有层相互连接,其表达式为

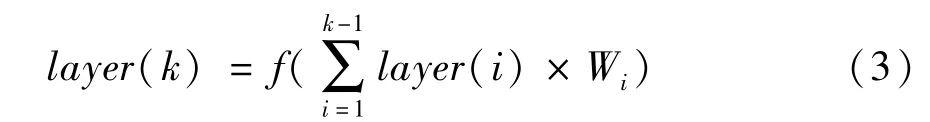
式中,layer(k) 为第k层的输出,Wi为卷积核,f(·)为激活函数。

这些卷积层的卷积核尺寸为3 ×3,特征个数为16,为了使卷积前后的图像尺寸保持不变,卷积前图像边缘进行补0 填充,填充尺寸(Padding)为1。

输入为由双三次插值为退化过程的低分辨率遥感图像,经过两组密集部分后通过反卷积增大图像尺寸,反卷积层的输出为256 个高分辨率特征图。最后的重建层由一个卷积层组成,尺寸为3 ×3,Padding 为1,通过这一层将256 个高分辨率特征图重建得到最终的高分辨率输出图像。

1.3 激活函数的改进

尽管使用了残差网络,网络在训练时仍然可能出现训练不易收敛的问题,ReLU 函数是斜坡函数,表达式为

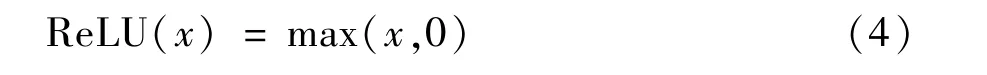
ReLU 函数将输入矩阵中所有负数都置为0,正值不变。此激活函数有一个缺点,就是训练很脆弱,很容易死亡。例如,当一个较大的梯度流过一个ReLU 神经元,更新后参数这个神经元就再也不会对任何数据有激活现象。那么在这之后此神经元的梯度永远都是0,也就是说ReLU 函数有时会在训练过程中不可逆地死亡,即在训练过程中有些神经元没有激活。因此,本文对ReLU 函数进行了改进,使用了PReLU 作为激活函数,PReLU 函数可以解决ReLU 函数的死亡问题,其表达式为

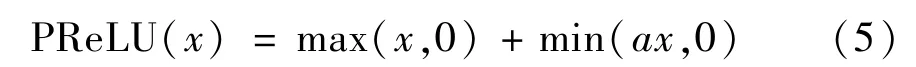
式中,a为较小的数,可取0.01。当x≥0 时,PReLU函数与ReLU 函数值都为x。但PReLU 函数比ReLU函数多了一项min(ax,0),当x <0 时,ReLU 函数为0,而PReLU 函数是一条斜率为a且过原点的直线。PReLU 函数只增加了极少的参数,网络计算量只增加了一点点,但网络在训练时健壮了很多。

1.4 学习规则的改进

DenseNet 网络训练的损失函数常用有L1范数和L2函数。L1范数损失函数也叫最小绝对值误差,总的来说是把目标值与估计值的绝对差值之和最小化。L2范数损失函数也叫最小平方误差,总的来说是使目标值与估计值差值的平方之和最小化。由于L1范数能处理数据中的异常值,其鲁棒性比L2更好,本文训练使用L1范数作为损失函数,训练的最终目标是使L1范数达到最小值。取实际高分辨率图像与重建后的图像的误差绝对值之和,其表达式为

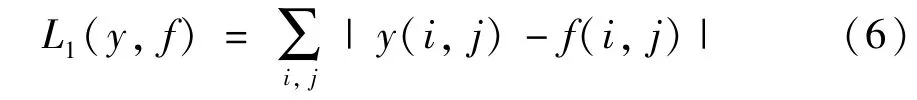
式中,y(i,j) 为实际高分辨率图像,f(i,j) 为重建后的图像。当L1范数达到最小值时,重建后的图像最接近于实际高分辨率图像。

网络优化器仍然采用Adam 优化器,它是一种可以替代传统随机梯度下降(stochastic gradient descent,SGD)过程的算法,Adam 算法的表达式如下:

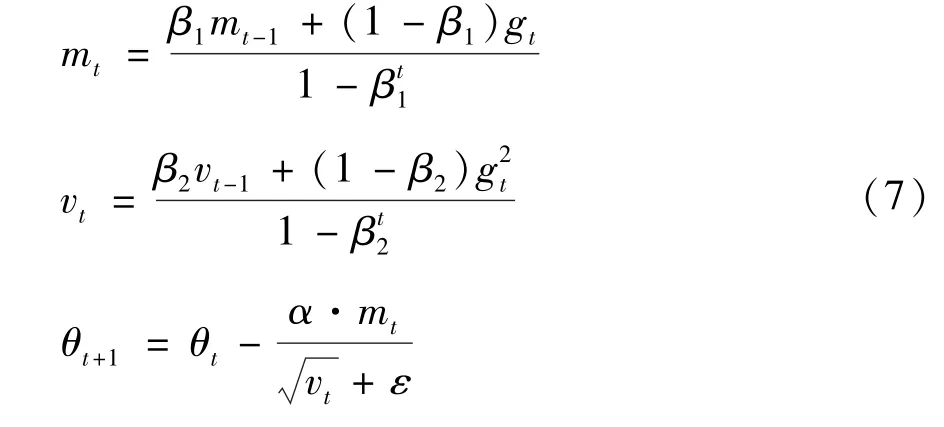
式中,β1、β2为参数,分别取0.9 和0.999。gt是t时间步的梯度,mt是对梯度的一阶矩估计,vt是对梯度的二阶矩估计,ε取10-8防止除数为0,α为初始学习率。

和传统的随机梯度下降不同,Adam 算法在训练过程中通过计算梯度的一阶矩估计和二阶矩估计,动态地调整学习率。而传统的随机梯度下降一直保持固定的学习率更新所有的权重。Adam 算法可以使每一次迭代的学习率都在一个较好的数值,使训练质量提高。Adam 的初始学习率α如果设得过大,学习速度则会非常快,但其收敛结果不好;α设得过小会导致训练时间过长,且对结果优化不大。因此,本文采用默认的初始学习率0.001,此数值既可以保证学习速度,又可以优化收敛结果。

2 实验与结果分析

2.1 网络训练实验过程

本文算法的实验环境为Intel Core I7-7700K CPU@4.20 GHz,16 GB 内存,64 位Ubuntu 系统,GPU为GTX1060,深度学习框架使用了TensorFlow 1.10。

训练样本使用合作单位提供的尺寸为20 000 ×20 000 的遥感图像。为了提高网络训练速度和训练样本数量,对每个小尺寸的遥感图像有交叉地截取为小图像,每相隔20 像素截取一张100 ×100 尺寸的小图像,最终得到超过8 万张尺寸为100 ×100 的小图像作为网络训练数据集。为保证数据集的数量,再将子图像分别旋转90 °、180 °、270 °,使数据集的数目增加了3 倍,最终得到了约2.5 万张100×100 的小图像作为训练集。将训练集图像本身作为网络的输出,训练集图像(2 倍欠采样)缩小2 倍到50 ×50,作为网络输入的低分辨率图像。

网络训练执行一次epoch 大约14 min,当训练epoch 达到35 次时,网络已经收敛,此时累计用时大约8 h。网络训练过程中误差与迭代次数的关系如图3 所示,网络的测试集峰值信噪比(peak signal to noise ratio,PSNR)与迭代次数的关系如图4 所示,每次epoch 训练后进行测试,约在35 次训练时PSNR 值接近了稳定。

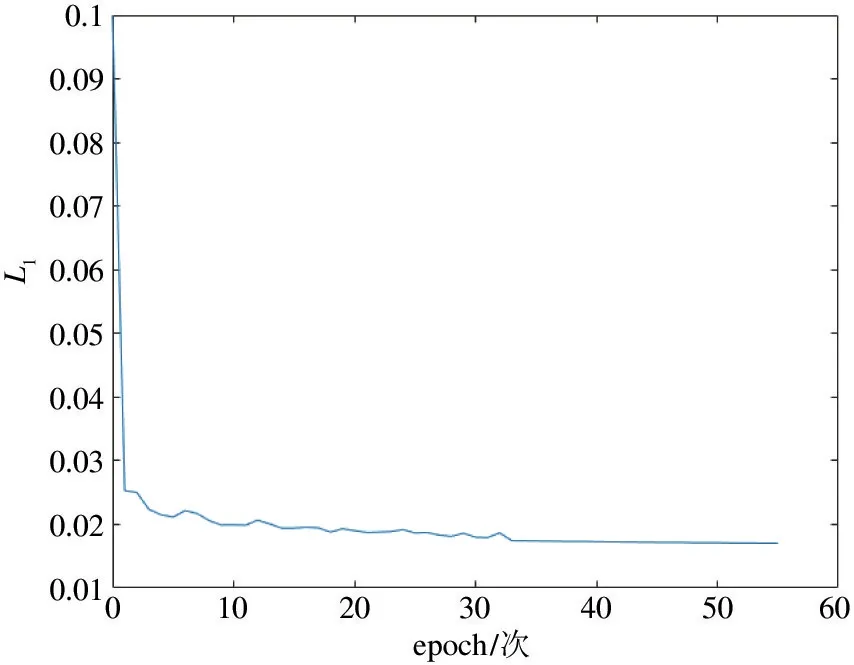
图3 网络训练误差与epoch 的关系

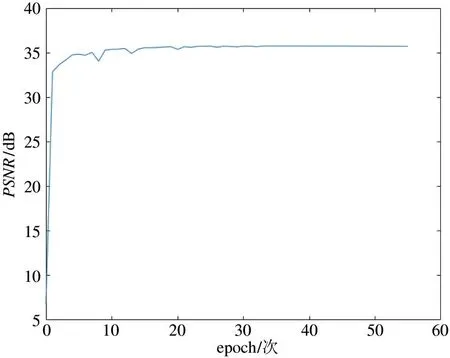
图4 测试集PSNR 与epoch 的关系

2.2 网络泛化实验结果与分析

取测试集PSNR 最大时的网络作为最终的结果进行泛化实验,此时epoch 为第35 次。在实验过程中,选取8 张遥感图像进行实验,如图5 所示。实验选择低分辨率图像、双三次插值、VDSR 算法、本文算法作对比。为了实验对比的合理性,实验中缩放因子都取2,训练与测试图像均使用遥感图像,在此列出4 组实验结果进行对比,遥感图像超分辨对比结果如图6～图9 所示。

图5 测试图像

图6 第1 组图像超分辨效果比较

图7 第2 组图像超分辨效果比较

图8 第3 组图像超分辨效果比较

图9 第4 组图像超分辨效果比较

由图6～图9 可以看出,与双三次差值与VDSR结果相比较,本文方法得到的超分辨结果视觉上更清晰,细节更丰富,地物细节更容易分辨出来。

为了客观地评价遥感图像超分辨重建效果,泛化实验中采用峰值信噪比(PSNR)和结构相似度(structural similarity,SSIM)作为超分辨算法的质量评价指标,其定义如式(8)和式(9)所示。

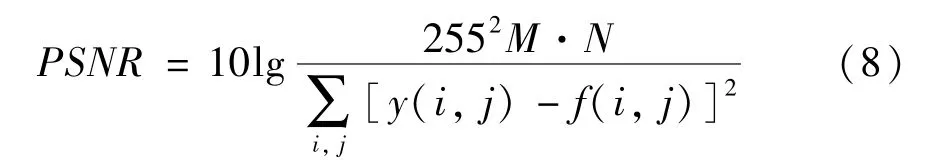
式中,y(i,j) 为实际高分辨率图像,f(i,j) 为重建后的图像。超分辨图像与实际高分辨率图像存在误差,其误差越小PSNR 越高,说明超分辨结果图像的失真度越低,重建效果越好。

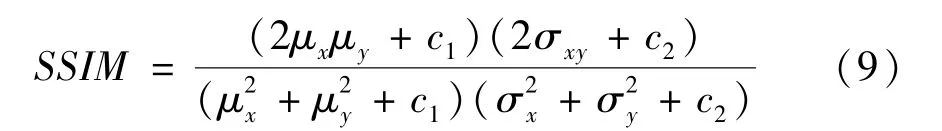
式中,μx、μy为均值,σx、σy为标准差,σxy为协方差,c1=(0.01L)2,c2=(0.03L)2,L=255。SSIM表示超分辨图像与实际高分辨率图像的结构相似程度,其取值为范围为[0,1],SSIM 越接近1 则说明它们的结构越相似,重建效果越好。

泛化实验统计的PSNR 和SSIM 结果分别如表1和表2 所示。综上所述,本文改进的密集连接网络遥感图像超分辨重建算法不论是主观视觉上还是在客观评价参数上,超分辨效果都优于其他算法。相比当前先进的VDSR 算法,本文算法其PSNR 平均提高约了1.05 dB,SSIM 平均提高了0.042。

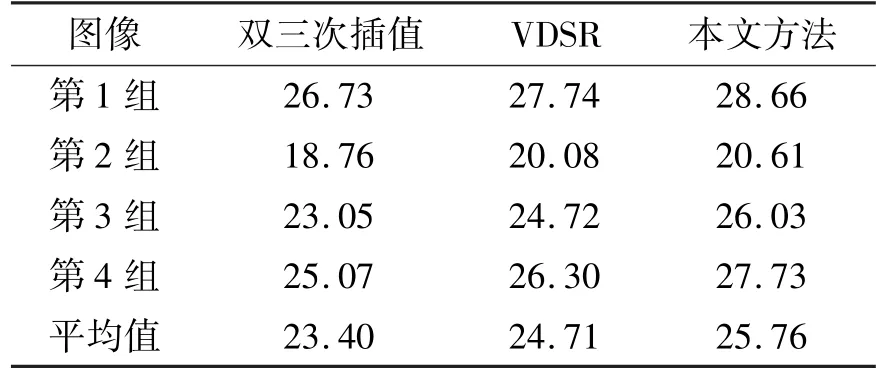
表1 3 种算法的PSNR 对比(dB)

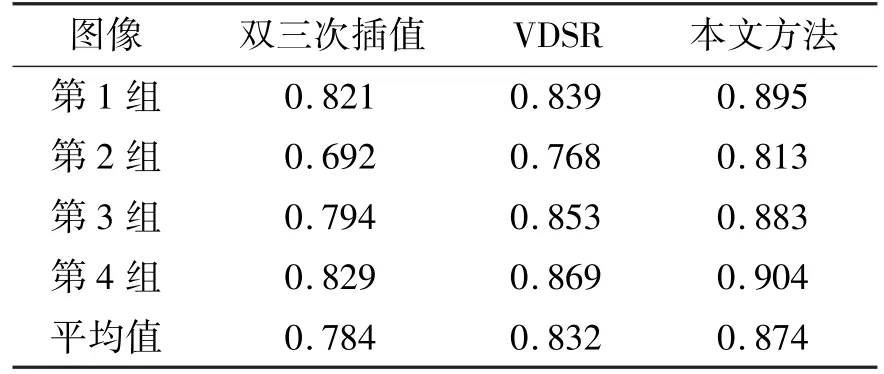
表2 3 种算法的SSIM 对比

3 结论

本文改进了VDSR 算法,网络训练与测试使用的数据集采用了遥感图像,结合了密集连接网络,将残差网络中的残差块替换成密集块,并增加了一组密集层与瓶颈层完成了网络结构的改进。同时,在激活函数、学习规则方面也进行了改进,修改网络激活函数为PReLU 函数,网络训练采用了L1损失函数。当训练的epoch 达到了大约35 次时网络已经收敛。

网络泛化实验结果表明,与VDSR 算法相比,本文改进的算法对遥感图像的效果更优。图像的超分辨结果在主观视觉上更清楚,细节信息更丰富,地物细节更容易分辨出来。客观评价指标PSNR 平均增加了1.05 dB,SSIM 平均增加了0.042。