双电极联合循环工作模式下阵列电极的传感能力分析①

张玉燕 贾 斌 温银堂③

(*燕山大学测试计量技术及仪器河北省重点实验室 秦皇岛066004)

(**燕山大学电气工程学院 秦皇岛066004)

0 引言

同面阵列电极传感技术是一种新兴的无损检测技术,是在电容层析成像(electrical capacitance tomography,ECT)技术基础上发展而来的[1-2]。将传感电极布置在一个平面内,使其具有独特的几何特点,传感电极可以从单平面接近被测物体。因此在很多测量空间受限的测量环境下,同面阵列电极相比圆周排布的电极更具优势,同时也具备非侵入性、响应快速、灵敏度高等优点。近些年,同面电极传感技术获得了海内外学者的关注,取得了较大的突破和成果[3-6]。

同面电极传感器主要利用非线性的边缘电场工作。当采用阵列形式时,敏感场具有“软场”特性,即电场中心位置的检测灵敏度相对较低,导致该位置处出现测量不准确、分辨率低等问题,具体表现为电场的分布不均匀。即使被测物体的介电常数处处相等,敏感场分布也不是均匀的,同时其分布还会随着被测物体的介电常数的改变而变化。考虑上述原因,同面电极的电极尺寸、形状、布置方式、工作模式等都在很大程度上影响其传感性能。因此,如何提高同面电极传感器的传感性能,如何使其能够更好地分辨出待测物介电常数场变化的大小和位置是关键的问题,非常值得且有待于深入研究和探讨。当前关于同面电极传感技术的研究主要包括电极设计及优化、成像算法和应用研究等方面。其中关于同面电极的改进和研究主要包括:(1)传感器极板的改进。文献[7]计算了同面8 电极传感器不同极板尺寸对实验中电容值的影响,最终得到长宽高为50 mm×50 mm×3 mm 的最佳尺寸组合。文献[8]针对加固混凝土结构的检测提出一种共面电容传感器模型,提高了共面传感器对待检测结构的穿透深度。文献[9]设计了5 种不同结构、不同形状的共面12 电极传感器,并对这5 种传感器进行了对比分析,得出性能最优的电极排列方式。(2)传感器电极数量的优化。文献[10]将共面4 电极传感器拓展到三维空间上的5 块共面4 电极传感器,这种三维空间上的20 电极传感器提升了待测物体三维重建的图像质量。文献[11]针对碳纤维材料的损伤模型设计出4 种不同电极形状的双电极传感器,通过敏感场和重建图像的效果对这4 种传感器进行了评价,验证了三角形双电极传感器相对于其他双电极传感器的结构优势。(3)屏蔽层的优化。文献[12]通过调整极间和边缘屏蔽的大小距离使敏感场和电容数据得到改善,证实了3 mm 的屏蔽宽度对传感器的性能改善明显。

在电容传感技术中,改变电极的激励方式也是一个优化传感器性能的途径,但目前大多都是针对多相流的ECT 成像技术。文献[13]将三层的传感器按照相同层和不同层电极2 种模式进行激励以提高成像的稳定性。文献[14,15]按照纵向模式将两对电极激励用以优化三维传感器对油气两相流检测的性能。文献[16]提出了一种差分电极传感器,这种分别对测量电极和差分电极进行激励的方式减少了检测过程中的噪声值,有益于更加精确的图像重建。对于同面阵列电极而言,文献[17]针对平面32电极电容传感器提出一种双激励的方式,仅是将每两块极板简单地组合在一起等效形成一种极板面积更大的16 电极传感器,然后进行单电极激励。对于电极数较少的12 电极平面阵列而言,如何通过改变电极的激励方式提高传感器的性能,还需要深入研究探讨。

本文针对同面3 ×4 阵列电极传感器,研究了一种新型的双电极循环激励方式,从传感器的探测深度、敏感场分布、电容动态范围、图像重建效果等方面对此模式下的电极传感能力进行了分析,以验证该激励模式对提高同面阵列电极电容传感器的检测能力和工作效率的有效性。

1 同面阵列电容成像传感原理

同面阵列电容成像系统由电极阵列传感器单元、电容采集单元和图像重建单元[18]这三部分组成,如图1 所示。

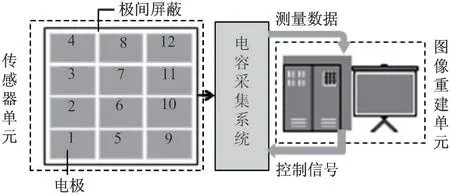
图1 同面阵列电容成像系统组成图

基于给定的几何模型、激励方法和电势分布的模拟过程,在待测物体的介质分布和敏感场边界条件全部已知的情况下,获取同面阵列电极传感器测得的电容值。这些电容数据可以间接反映出被测物场的介质分布情况。

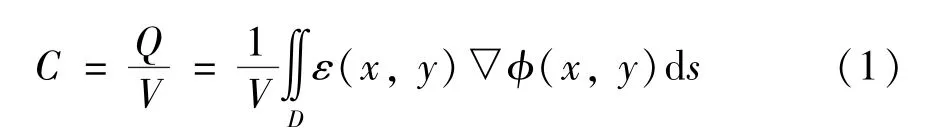
式中,Q为电极上的感应电荷,V为电极对i -j之间的电位差(i,j=1,2,…,n),在12 电极中n=12。

对于一个电极个数为n的传感器,可以获取的电容值个数为M=n(n -1)/2,本文所述的同面阵列12 电极电容传感器可得到66 组电容值。

每两块电极极板之间的电容为

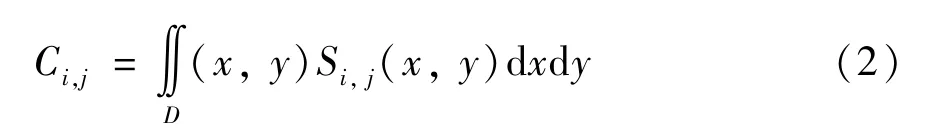
其中,Si,j(x,y) 为两块电极之间的电容Cij的灵敏度函数。

电容向量C(C1,C2,…,Cn)的L2范数定义为

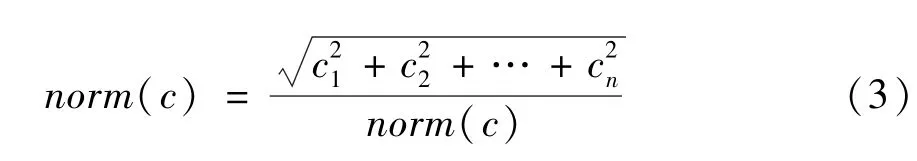
其中c1、c2、…、cn表示电容向量C中的电容数据元素。

建立从C到C′的映射,使C′的L2范数为1:

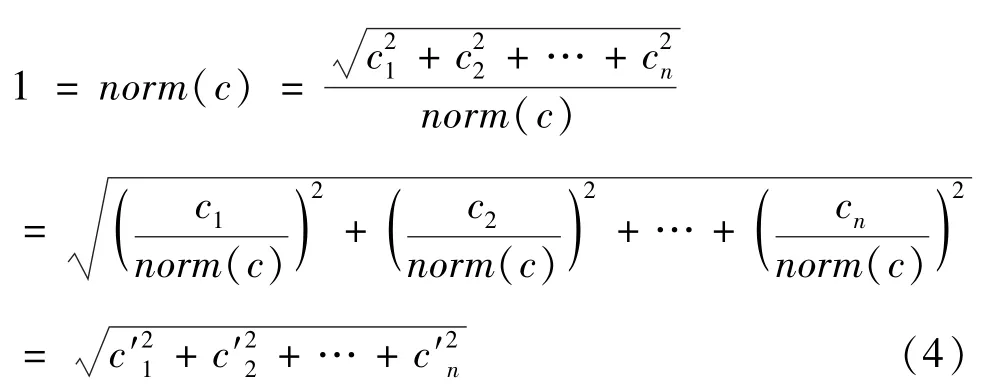
由式(4)可知电容数据的L2范数归一化的结果为

其中,表示归一化后的电容数据元素。

求取介电常数的分布场:

其中,C和S为经过归一化处理的电容矢量和介电常数矢量。

由式(6)可知,由获取的电容值可反求出测量物场内介电常数分布场G,即进行图像重建。通过重建出的图像可以较直观地反映出测量物场的变化。典型的图像重建算法可分为智能优化、非迭代和迭代这三大类。

2 联合循环激励测量方案

2.1 同面3 ×4 阵列电极模型

本文针对一种同面3 ×4 阵列电容传感器进行研究,所建立的12 电极模型图如图2 所示。

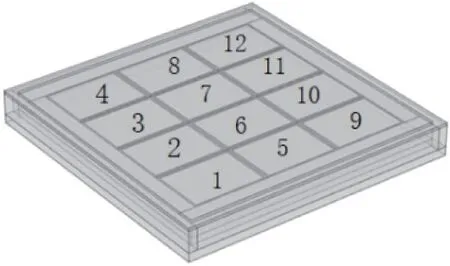
图2 同面阵列电容传感器模型

2.2 激励方式

通常电极采取单电极循环激励方式。在一个工作周期内,顺序选取一块电极作为激励电极,其他电极均作为接地电极,然后其他电极轮流激励,至12块极板均完成激励。获取激励电极与接地电极的电容值,最终可得到66 组有效电容数据。当被测物场介电常数变化很小时,该方式下电场比较微弱,数据易受干扰。

因此,本文针对这一问题,提出了一种双电极联合循环激励测量模式,将12 块极板按顺序两两联合,采用循环组合激励方式,其激励的顺序如图3 所示。图中给出了电极编号,首先将1 号电极和2 号电极联合激励,分别测量3-4、5-6、7-8、9-10、11-12 这5 组联合接地电极与1-2 联合电极之间的电容值;然后将2 号电极和3 号电极共同激励,同样将其他10 个电极作联合接地处理,获取4-5、6-7、8-9、10-11、12-1 这5 对接地电极与激励电极2-3 的电容值;按照箭头所示的组合方向依次激励直至编号为12和1 的2 块电极共同激励为止,得到C1-2,3-4,…,C12-1,10-11共30 组电容值。

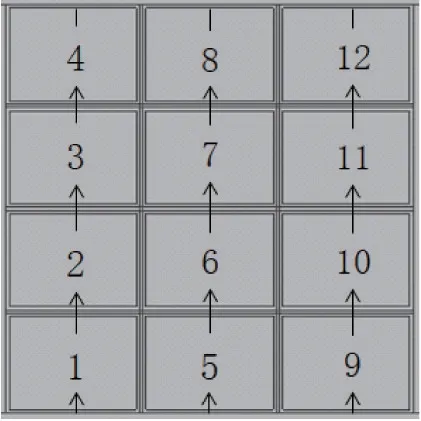
图3 电极联合循环激励顺序图

电容数据矩阵如下所示:

3 联合激励模式的仿真

为了研究新的联合方式对3 ×4 阵列电极的传感能力的影响,分别从传感器的穿透深度、敏感场、电容值、检测效率和图像重建质量方面,与传统单电极激励方式进行对比研究。本文利用COMSOL Multiphysics 对阵列电极传感器进行建模,被测物场的相对介电常数为3.5。

3.1 传感器探测深度和敏感场均匀性

首先给出空场条件下2 种激励方式的电势分布图用来比较2 种模式的穿透深度。取一对电极电势分布为例,如图4 所示。图4(a)为单电极激励方式下编号为1 的电极作为激励电极,编号为2 的电极作为接地电极的电势分布切面图;图4(b)为联合激励方式下1-2 号电极同时作为激励电极,3-4 号电极同时作为接地电极的电势分布切面图。

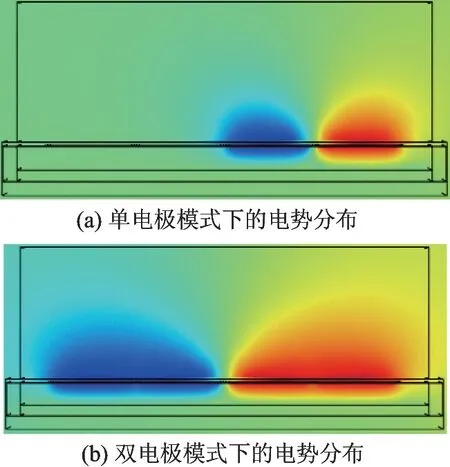
图4 电势分布图

由图4 可知,与单电极激励模式相比,双电极联合循环激励模式下的电势覆盖范围更广,穿透能力更强。

在3 ×4 阵列极板上方空间添加相对介电常数为3.5、底面积为150 mm×150 mm 的长方体作为待测物体,如图5 所示。逐渐加高待测物体,分别在2种激励方式下,对不同厚度的被测物场进行电容数据测量。

图5 待测物体示意图

由图6 可知,单电极激励测量模式下待测物体厚度在1～13 mm 下电容的最大值逐渐增大且保持一定的增长幅度,之后增幅减小,在高度为20 mm左右达到最大值,数值在0.58 pF,之后电容最大值随高度的增加而减小。

所获得的电容测量数据的最大值与被测物厚度的关系曲线如图6 所示。

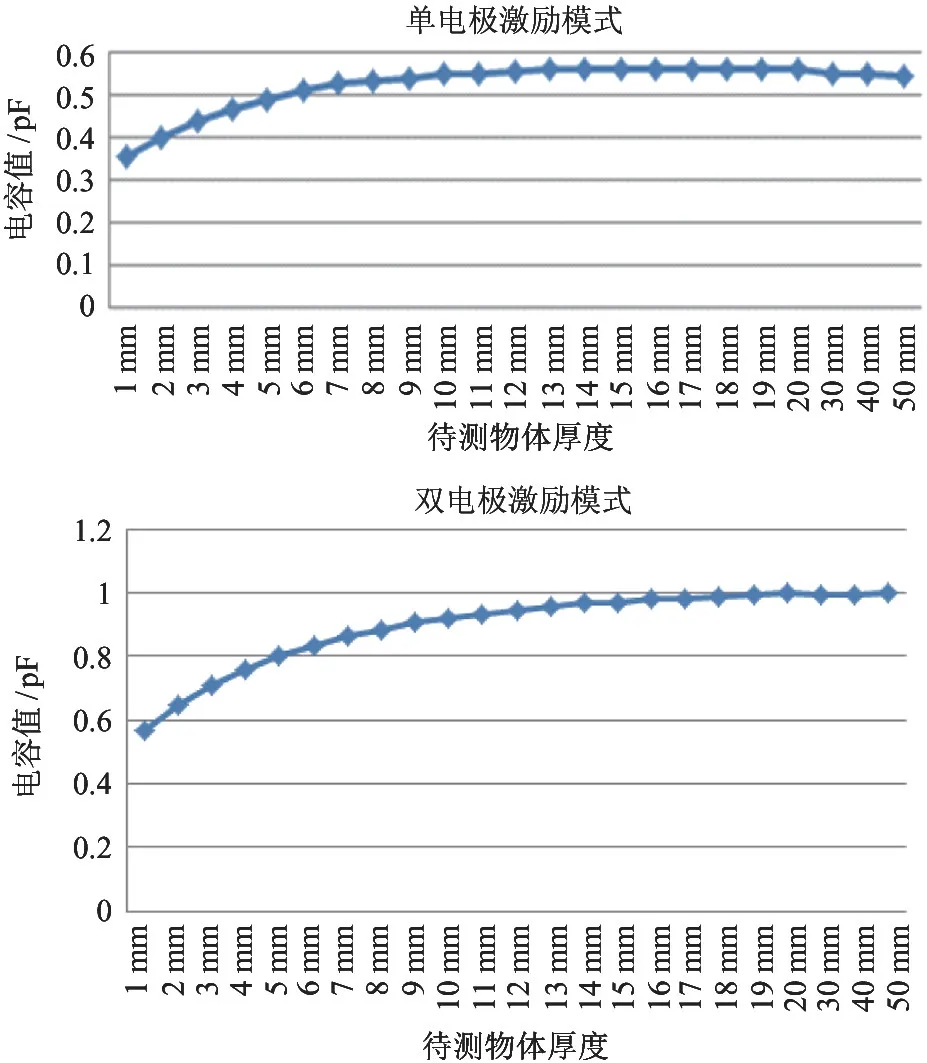
图6 电容最大值对比

在双电极的联合循环激励测量模式下待测物体高度在1～16 mm 下的电容最大值逐渐增大且保持一定的增大程度,在30 mm 左右电容达到最大值,之后当被测物厚度增加时电容数值基本保持不变,数值在1 pF 左右。相比单电极激励方式,其最大穿透深度有所增加,对应的电容数据增大近一倍。

为进一步分析激励模式改变对电极灵敏度的影响,基于有限元方法建立了3 ×4 阵列电极的灵敏场模型,计算得到灵敏度矩阵。本文选取灵敏度矩阵中数据的离散系数(coefficient of variance,CV)作为评判其均匀性好坏的标准。

式中σ为灵敏度矩阵的均方差,μ为灵敏度矩阵的算术平均值。

根据CV 的计算数值对其均匀性进行判断,CV越小分布越均匀。2 种激励方式CV 的值如表1 所示。

表1 2 种激励方式下敏感场的CV 值

由表1 可知,在双电极联合循环激励测量模式下该同面阵列12 电极电容传感器的CV 值更小,敏感场更加均匀。

为深入讨论灵敏场的分布特性,对灵敏度矩阵进行了可视化3D 重建,如图7 所示。单电极激励模式下,以6 和7 电极对的灵敏度图像为例,双电极激励测量模式下,以5-6 联合和7-8 联合两组电极对的灵敏度图像为例,选取第2、4、6、8 层的图像进行对比分析。

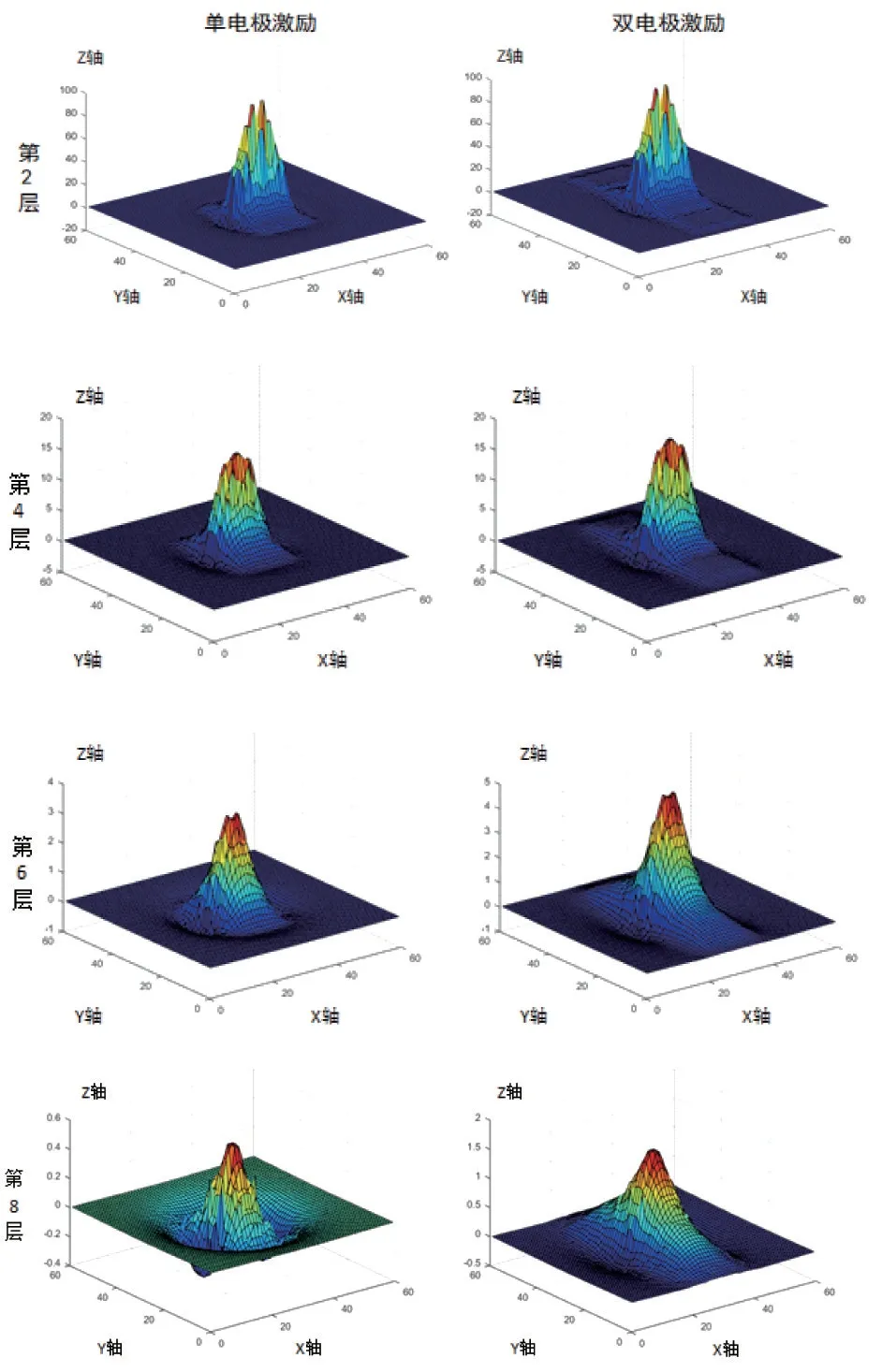
图7 第2、4、6、8 层敏感场矩阵分布图

由图7 可知,越高层的敏感场数值越低,对介电常数的感应能力越弱,在双电极联合循环激励测量模式下其敏感场矩阵每层的数值均大于单电极激励测量模式,更有利于反映待测物体的介电常数变化。

综合上述图表内容可知,当该同面阵列电容传感器采用双电极联合循环激励方式时,传感器的电极对待测物体的穿透能力更强,敏感场分布更均匀,更有利于对待测物体的检测和重建。

3.2 电容数据分析

阵列电极工作中,所获得的电容数据的动态范围和动态特征在很大程度上能反映传感能力。

首先分析空场条件下的电容数据,2 种激励测量模式的数据折线如图8 所示。

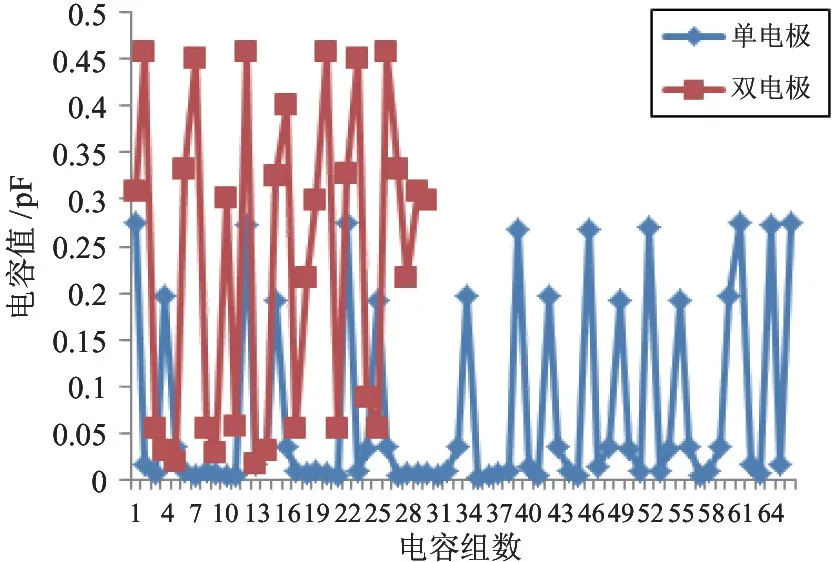
图8 2 种激励方式在空场条件下的电容值折线图

由图8 看出,双电极联合循环激励测量模式能够获得更大的空场电容值,并且30 组电容值围绕其平均值0.23 pF 上下波动。空场电容值的动态范围和电容的最值,如表2 所示。

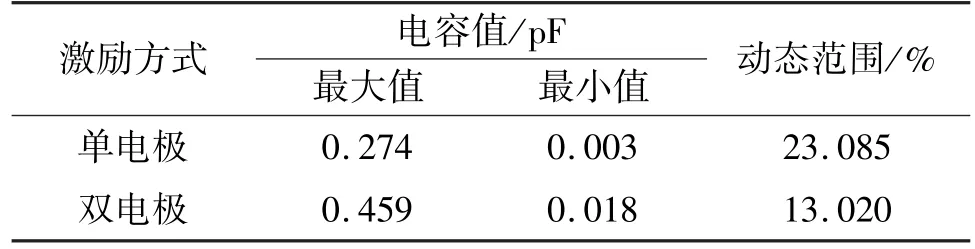
表2 空场电容最值及其动态范围

由表2 可知在空场条件下新型的双激励循环测量方式最值均大于单电极激励测量方式,且其动态范围减小了43.6%。

其次考虑阵列电极对不同的被测物场的传感能力,本文建立3 种物场模型。被测物体选用高度为0.2 cm、半径为2 cm 的圆柱体,改变圆柱体个数和位置来设置不同的物场条件。图9 给出了3 种物场模型图,模型1 中只有一个圆柱体,放置在阵列电极的中心位置,模型2 中2 个圆柱体对称放于中心的两侧,模型3 中将4 个圆柱体对称放于中心的四周。

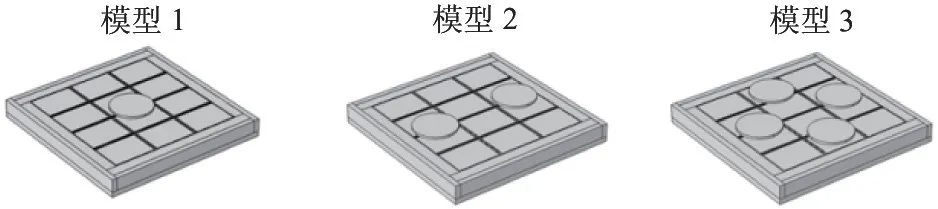
图9 被测物场模型

针对3 种物场模型分别获取它们原始电容的平均值,如表3 所示。

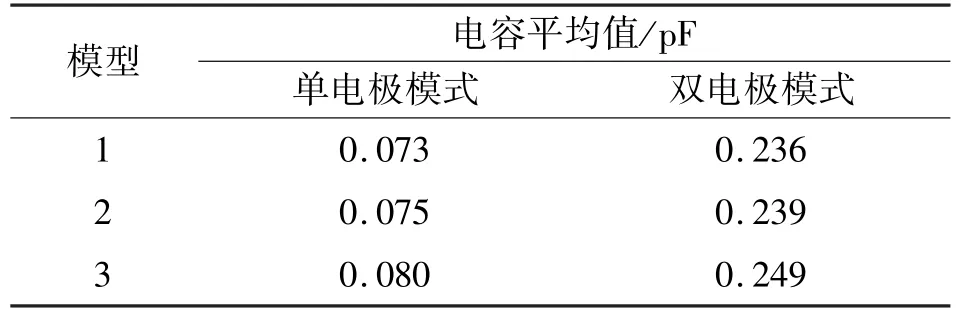
表3 3 种被测物场电容数据平均值

由表3 可知,3 种物场模型均能在双电极联合循环激励方式下获取更大的电容值,更大的电容值意味着更强的电场强度,因而也间接验证了3.1 节的结论。结合空场模型的电容数据可知,更大的电容值降低了对电容数据采集系统的设计难度,同时增强了传感器的穿透深度。

为了归纳数据的分布,本文将3 种模型在2 种不同激励方式下电容值进行范数归一化处理后进行比较,折线图如图10 所示。

由图10 可知,在2 种激励模式下,阵列电极电容数据曲线都有明显的波峰,波峰的位置能很好地反映出待测物的数量和大致位置。但通过比较发现,双电极联合循环模式下在非波峰位置的电容数据动态范围和数据均值要明显小于单电极激励模式,3 种物场模型电容数据值都反映了这样的规律。这说明双电极联合循环模式下,电容数据的噪声电平更小,数据稳定性更高,更有利于反映出因物场变化所带来的电容值变化量。

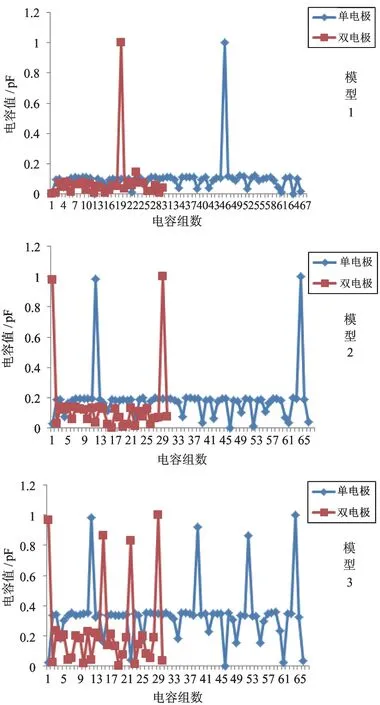
图10 3 种模型的电容值折线图

综上可知,空场和物场电容数据的特征表明了双电极联合循环模式下电容数据稳定性相比单电极模式有所提升,更有利于提高平面阵列电极的信噪比以及改善后期图像重建质量。

3.3 检测效率分析

本文以图9 所示的模型3 作为研究对象,研究2 种激励方式在Tikhonov、LBP(local binary pattern)、Landweber[19-20]3 种算法下的图像重构效率,其重建所需时间如表4 所示。

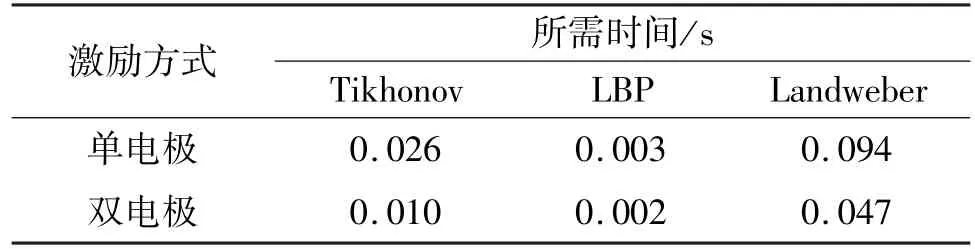
表4 2 种模式重建所需时间

由表4 可知,同种重建算法之下双电极模式所获取的电容值重建所需时间小于单电极模式。因此在实际应用中双电极的循环激励方式采集的数据量更少且重建速度更快,在不影响重建质量的前提之下,其检测效率大幅提高。

3.4 图像重建质量分析

首先分析新型激励方式在不同的重建算法下的图像重建效果。图11 给出了Landweber 算法实现的流程图。

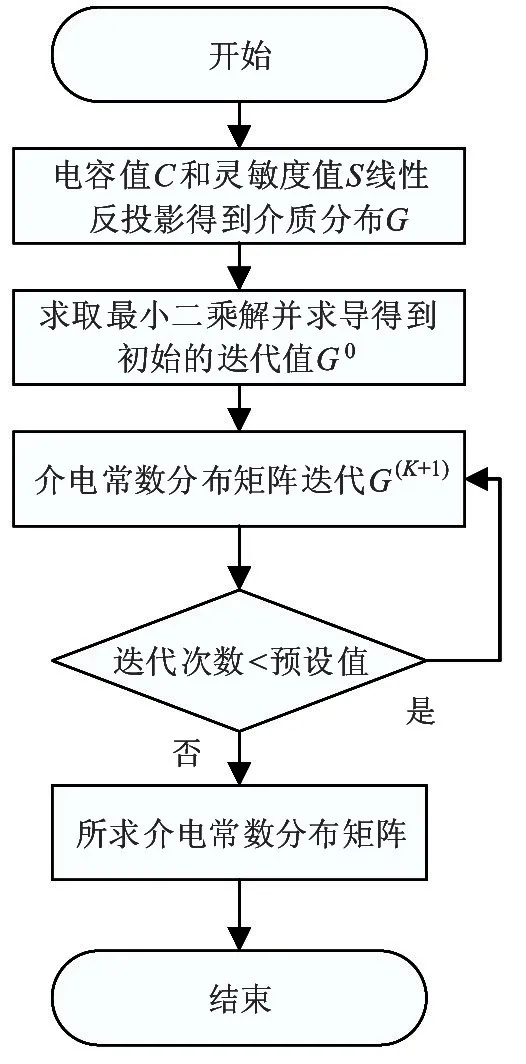
图11 Landweber 算法

将Tikhonov 和Landweber 算法下的重建图像进行对比分析。

Tikhonov 正则化算法定义为

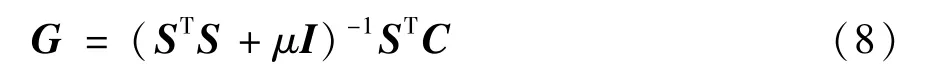
其中,G表示介电常数分布矩阵,μ表示正则化参数,I表示单位矩阵。

Landweber 的迭代公式为

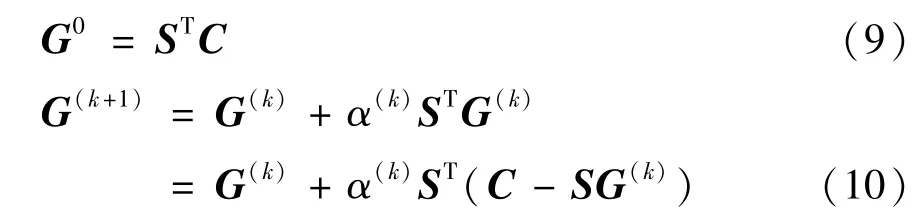
其中,G0为初始迭代值,α表示一个正的标量,G(k+1)表示对介电常数分布矩阵的第k +1 次迭代,在本文中迭代次数选取为5 次。

对图9 所示3 种模型中的模型3 进行图像重建,重建效果图如图12 所示。

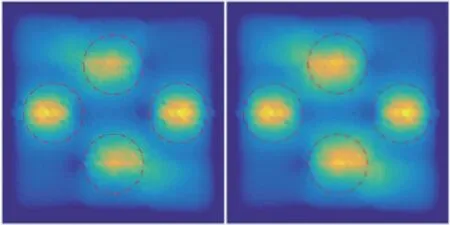
图12 Tikhonov 和Landweber 下的重建图像

图12 已将检测空间中4 个待测物的位置信息用虚线标识。相较于图12 中左侧的Tikhonov 算法的重建图像,位于右侧的Landweber 算法下的重建图像能够更加清晰地描述待测物体的位置和形状信息,重建效果相对更佳。

对图9 所示3 种物场模型的电容数据进行5 次迭代的Landweber 算法图像重建。在重建的图像中由红色到蓝色表示介电常数由大到小。又因为2 种激励方式在Landweber 算法下的重建图像均存在较大的伪影,因此本文根据重建出来的彩色图像获取其中的红色分量,以此红色分量图中的高亮部分作为3 种仿真模型的圆柱形物体,这种红色分量图更易于观测和提取面积占比。以重建图像与仿真物场的图像相关系数作为量化评判重建图像质量的标准。重建图像如图13 所示。

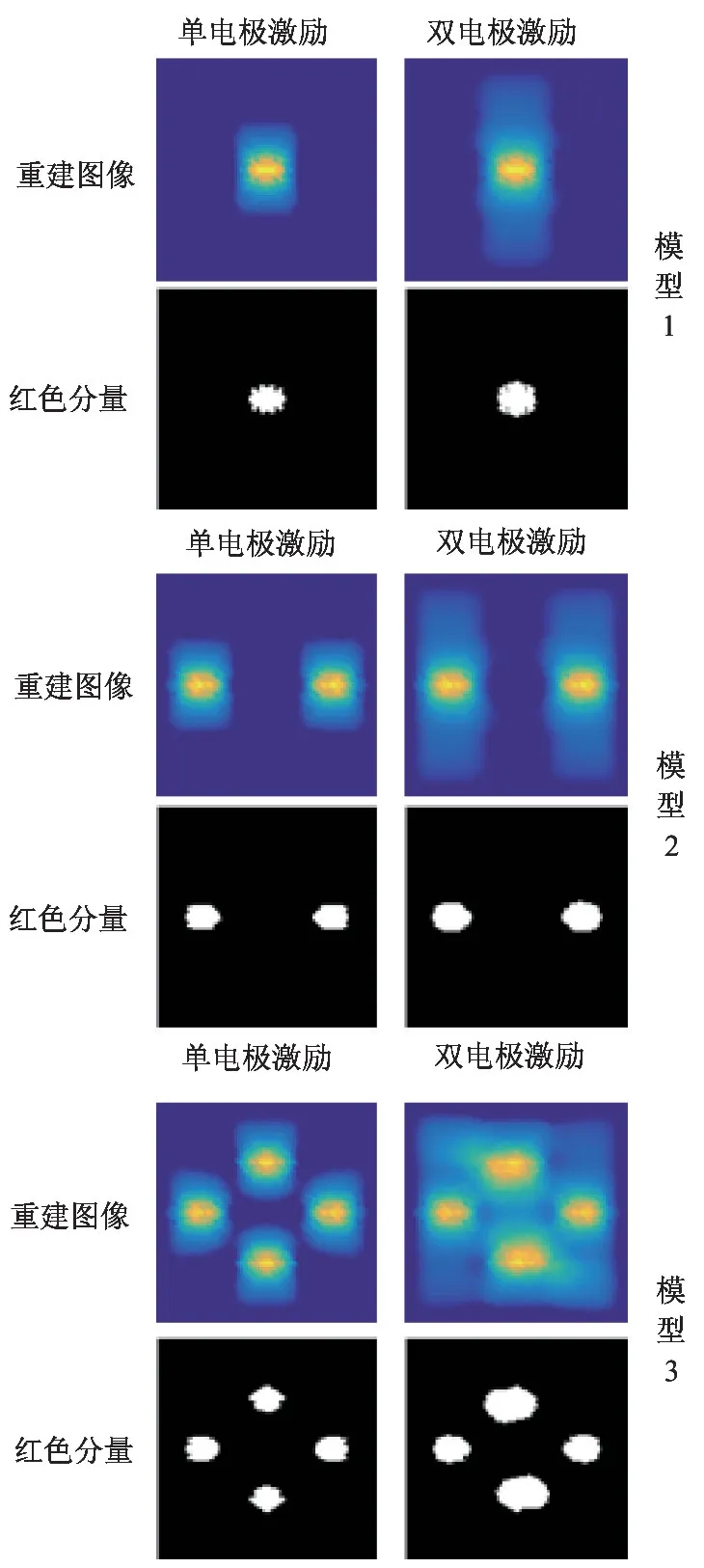
图13 重建模型和图像红色分量

红色分量提取图和实际物场的相对系数如表5所示。

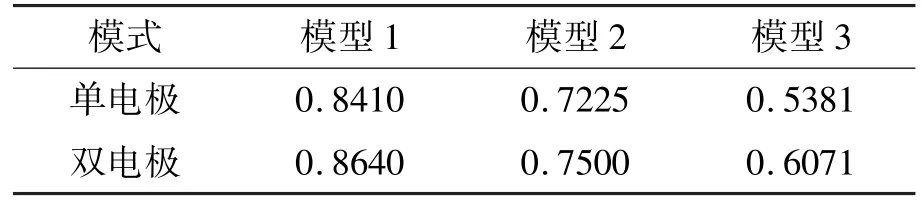
表5 图像相关系数

由表5 可知,3 种模型在双电极激励测量方式下的图像相关系数更大,重建图像的质量更高,有助于对待测物场的重建图像的定量分析。

模型1 的创建展示了模型在极板中心的重建情况,由图13 可知双电极激励方式下的重建图像外形轮廓更清晰。由表5 可知其红色分量提取图与真实物场的相关系数增加了2.7%,因此可知双电极激励测量模式下极板中心的重建图像质量更高。

模型2 和模型3 考察了多个物体在极板四周的重建情况,由表5 可知图像重建与真实物场的相关系数会随圆柱形物体的增多而变小;当采用双电极激励方式时重建图像与真实图像的相关系数分别增加了3.7%和11.4%,因此采用新型的激励模式能更好地提高图像质量。

4 结论

本文研究讨论了基于同面3 ×4 阵列电极电容传感器的双电极联合循环激励方式,并比较分析了联合循环的激励测量方式与单电极激励测量方式的参数数据和重建图像。最终结果表明,同面3 ×4 阵列电极传感器在联合循环激励测量模式下的检测效率和重建图像质量均得到了提高。本文不仅为同面阵列电极的优化设计提出了新的研究思路,同时因为这种新型激励测量模式增强了传感器的穿透能力,使同面阵列电容成像的应用范围得到了拓展。本文的下一步工作是将新型激励测量模式的成像方式从对待测物的层析成像转化为三维空间上的成像进行研究分析。