准Z 源逆变器自适应级联模型预测控制①

吴 春 杨佳磊

(浙江工业大学信息工程学院 杭州310023)

0 引言

2002 年,文献[1]提出了Z 源逆变器(Z-source inverter,ZSI),作为一种具有升压功能逆变器拓扑,它的出现有效解决了传统电压源逆变器(voltagesource inverter,VSI)输出相电压幅值受输入母线电压限制的局限性。ZSI 作为一种单级式逆变器拓扑,其电压调节范围宽,允许上下桥臂同时导通以实现升压功能,避免了由死区引起的输出波形畸变。因此,ZSI 在光伏系统中具有非常广泛的应用[2-3]。然而,ZSI 的阻抗网络存在电容电压应力大、启动时冲击电流大、输入电流断续等缺点[4]。准Z 源逆变器(quasi-ZSI,qZSI)改进了Z 源逆变器,其在继承ZSI 优点的基础上,具有电容电压应力小、输入电流连续等优点[5]。

有限集模型预测控制具有控制方法简单、无需调制、响应速度快、能同时处理多变量和非线性约束等优点,在电力电子、电机控制等领域得到了广泛的应用[6]。目前,已有不少研究者将有限集模型预测控制(finite control set-model predictive control,FCSMPC)应用于qZSI 系统中[7-8],并取得了良好的控制效果。文献[7]计算了由电感电流、电容电压和输出相电流三者组合而成的且包含3 个权重系数的代价函数,以此来获得下一个控制周期的最优开关状态。但是,权重系数的选取往往基于经验调试,当存在多个权重项的时候,选择一组合适的权重系数具有不小的难度[9]。

为了消除模型预测控制中权重系数,文献[10]将一种级联模型预测控制(sequential-model predictive control,S-MPC)策略应用于电机控制中,该策略首先计算转矩的代价函数,选择转矩误差最小的两个开关状态,然后将这两个开关状态代入到磁链代价函数,选择使磁链误差最小的开关状态作为下一个控制周期的最优开关状态。文献[11]和文献[12]分别将S-MPC 策略应用于三电平逆变器和交流/交流变换器中,通过将所选取被控对象的代价函数进行先后计算,从而消除了模型预测控制中的权重系数。

由于模型预测控制的性能依赖于精确的模型参数[13-14],因此基于模型预测控制设计的准Z 源逆变器,其控制性能依赖于模型精度。在文献[15,16]的研究中,均是以精确模型参数为前提条件,然而在很多场合,设计者无法获得准确参数,并且参数还会随着温度、磁场饱和程度等的变化而改变,使得控制性能下降。为了解决模型预测控制依赖准确参数的问题,国内外学者对此展开了研究[17-19]。文献[20]通过在线参数辨识方法,实时更新模型,但复杂的参数辨识方法会增加系统的计算量。文献[21,22]采用自适应控制方法解决了模型预测控制依赖精确模型参数的弊端,使系统具有较强鲁棒性。

本文针对qZSI 系统中控制变量多、参数易摄动的特点,提出一种适用于qZSI 的自适应级联模型预测控制(adaptive sequential-model predictive control,AS-MPC)策略。首先推导qZSI 中电感电流、电容电压和输出电流的离散模型,并根据控制对象优先级设计S-MPC 策略实现对上述3 个控制量的有效控制。同时,引入负载电气参数摄动自适应控制律,对系统总扰动进行实时估计,削弱负载电气参数误差对系统控制性能的影响。并且,为了消除数字控制器中输出延迟所带来的负面影响,加入延迟补偿策略。另外,利用矢量角补偿法来获得输出电流的未来参考值[23]。最后通过实验验证了所提出的ASMPC 策略在qZSI 中的可行性,同时分析其稳态性能、动态性能以及参数自适应能力。

1 qZSI 数学模型

qZSI 系统的拓扑结构如图1 所示,主要由直流电源、准Z 源阻抗网络、三相逆变桥和RL负载等组成。qZSI 可分为非直通状态和直通状态两种工作状态。其中,非直通状态类似VSI 的工作状态,而直通状态指上下桥臂同时导通从而实现直流母线升压目的。表1 列出qZSI 中所有可能的开关状态及其在α、β轴上电压分量,表中为逆变器侧母线峰值电压。

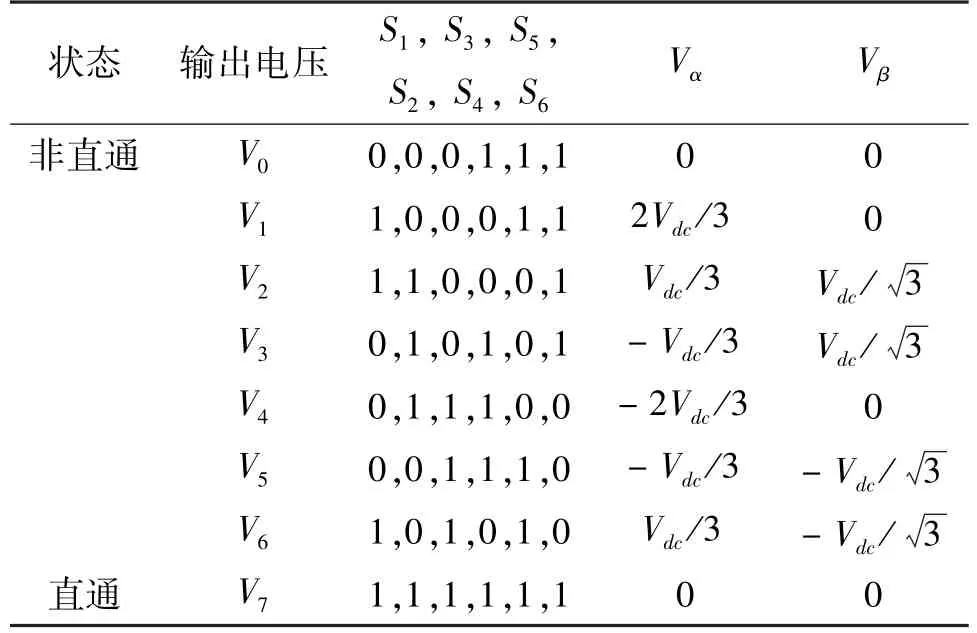
表1 开关状态表

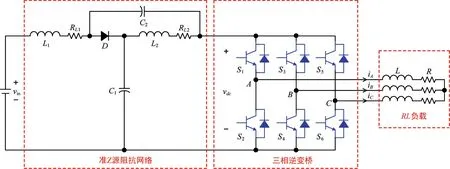
图1 qZSI 拓扑结构

由PARK 变换可得:

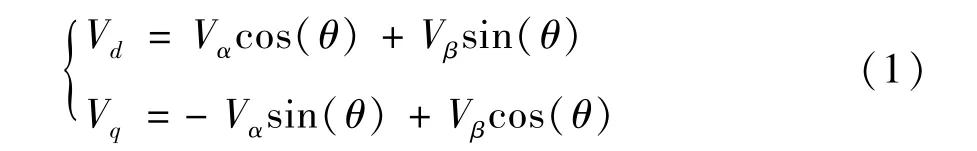
式中,θ为d轴与α轴之间的夹角,Vd、Vq为d、q轴上的电压分量。在d、q轴同步旋转坐标系上,输出电压方程为

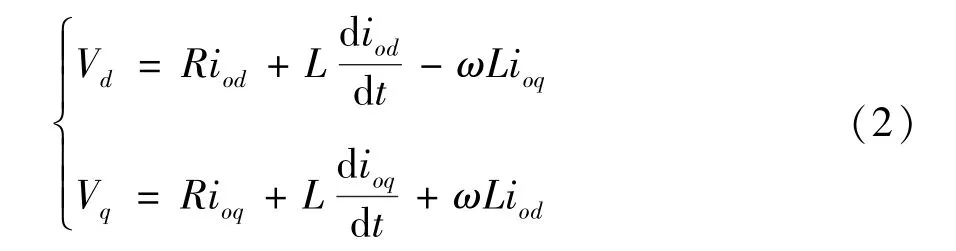
式中,R、L为负载相电阻和相电感,iod、ioq为输出电流在d、q轴上的电流分量,ω表示角频率。

令系统采样周期为Ts,用前向欧拉公式对式(2)在第k时刻离散化,得到预测模型:

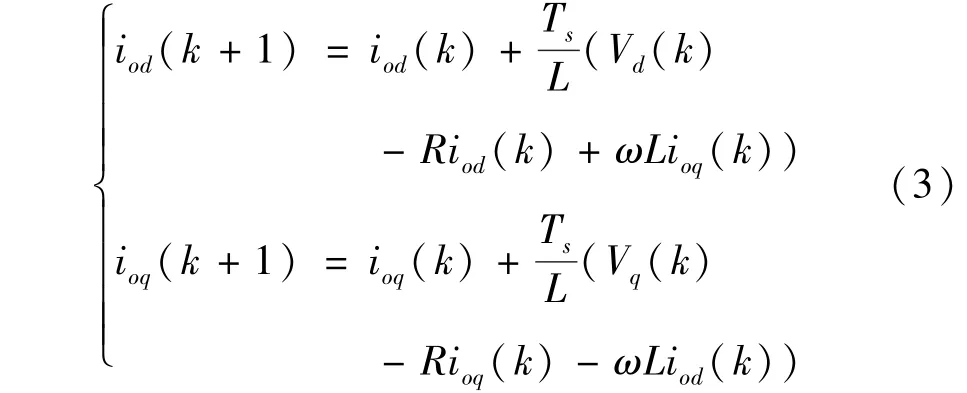
式中,iod(k)、ioq(k)为第k个采样时刻的电流采样值在d、q轴上的分量,iod(k+1)、ioq(k+1)为第(k+1)个采样时刻的电流预测值在d、q轴上的分量。

(1)当qZSI 处于非直通状态时,逆变桥可以等效为一个电流源iinv(k),该电流源可以表示为开关状态的函数。此时直流电源vin(k)与阻抗电感给负载和阻抗电容供电,二极管D正向导通,等效电路如图2(a)所示。电感电流和电容电压可以表示为

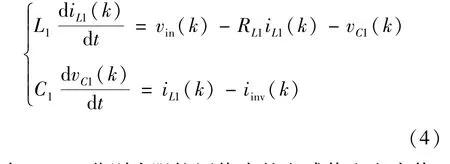
式中,L1、C1分别为阻抗网络中的电感值和电容值,RL1为电感L1的杂散电阻,iL1(k)和vC1(k)分别为第k个采样时刻电感电流和电容电压的采样值,iinv(k)=iA(k)SA+iB(k)SB+iC(k)SC,iA(k)、iB(k)和iC(k)为第k个采样时刻A相、B相和C相的电流值。

用前向欧拉公式对式(4)在第k时刻离散化,得到预测模型如式(5)所示。

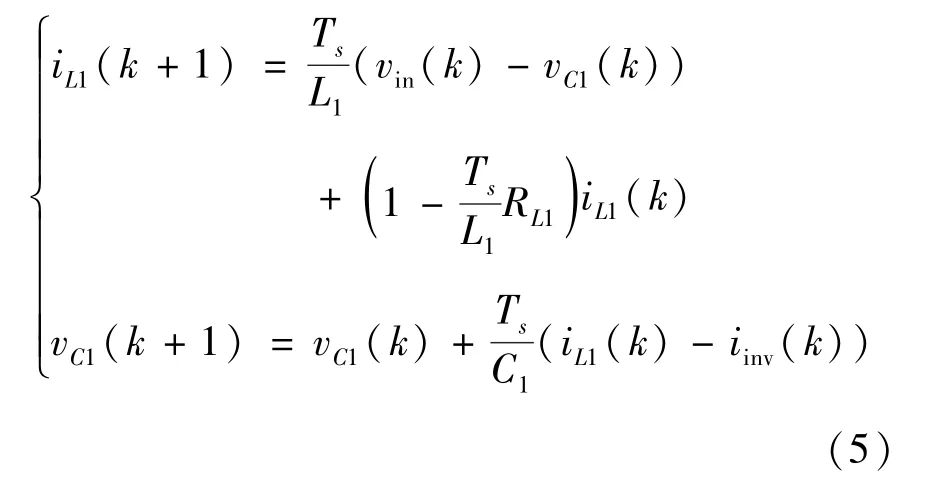
(2)当qZSI 处于直通状态时,逆变桥上下桥臂同时导通。此时,直流电源vin和阻抗电容同时给阻抗电感充电,二极管D反向截止,等效电路如图2(b)所示。电感电流和电容电压可以表示为

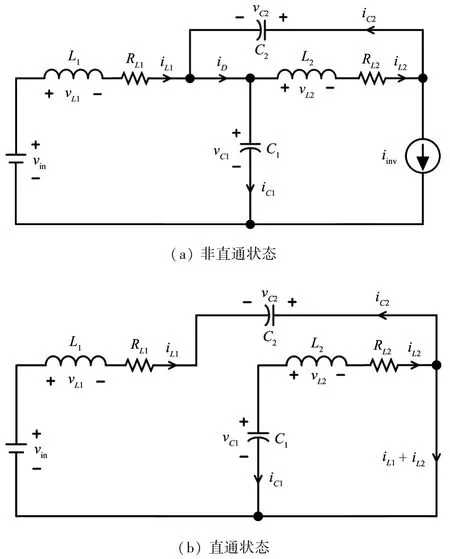
图2 两种状态下qZSI 等效电路

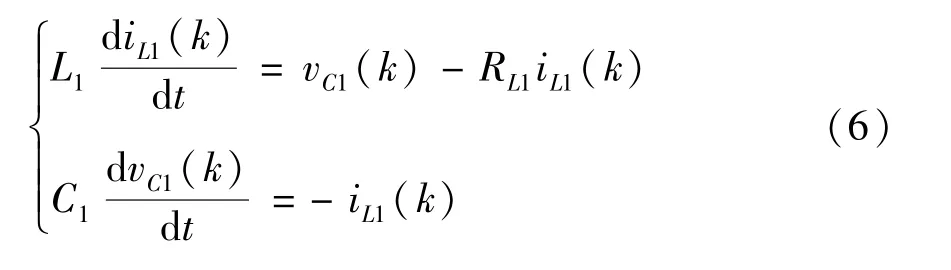
用前向欧拉公式对式(6)在第k时刻离散化得:

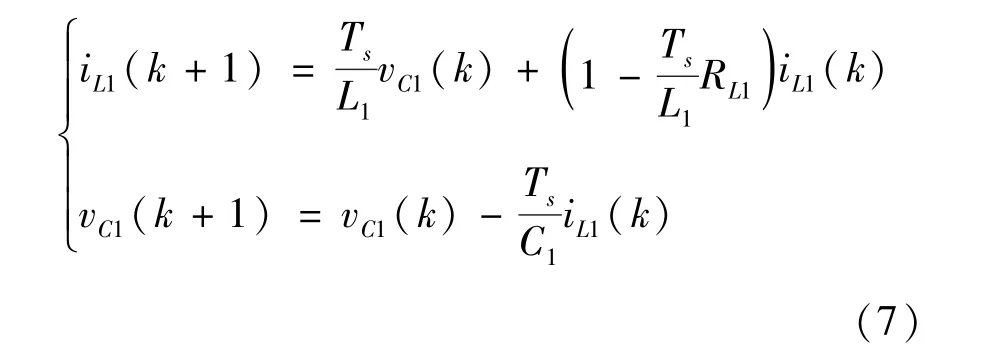
2 qZSI 的传统FCS-MPC 控制策略

由于在qZSI 系统中,输入电感电流、电容电压和输出电流都需要控制,因此在FCS-MPC 策略中,qZSI 的代价函数需要3 个权重系数,如式(8)所示[7]。

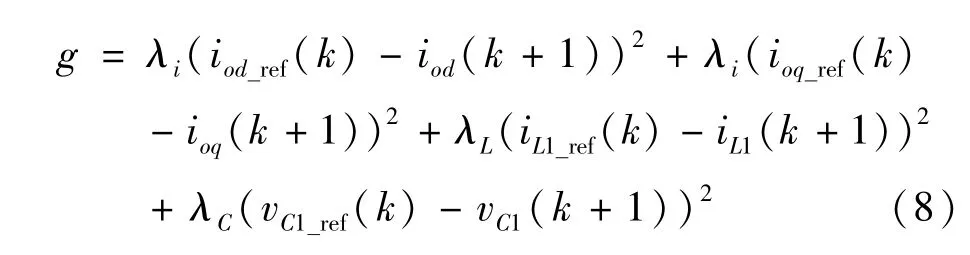
式中,vC1_ref(k)和iL1_ref(k)分别是电容电压参考值和电感电流参考值;iod_ref(k)和ioq_ref(k)为输出电流参考值;λi、λL、λC分别为输出电流、电感电流和电容电压的权重系数,只有选取合适的权重系数,qZSI才能正常工作。

对于图1 中负载参数已知的独立负载,通过式(9)可以得到控制对象各个控制量的参考值。

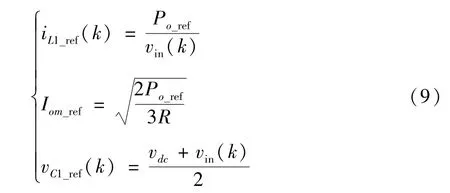
式中,Po_ref、Iom_ref分别为参考输出功率、参考输出电流的相电流幅值。

3 级联模型预测控制策略设计

由式(8)可知,传统FCS-MPC 中代价函数存在3 个权重系数,由于缺乏合适的权重系数整定原则,因此增加了系统调试的难度。S-MPC 策略的出现很好地解决了FCS-MPC 权重难以整定的问题,对于存在多个被控对象的系统,提供了一种简单且实用的方法。

3.1 级联模型预测控制策略设计

由于阻抗网络中电感电流的特殊性,当qZSI 处于非直通状态时,电感电流下降;当qZSI 处于直通状态时,电感电流上升。由此,可以根据电感电流的预测值来判断下一个控制周期是否为直通状态[8]。若判断下一个控制周期为直通状态,则直接输出直通矢量;若为非直通状态,根据级联模型预测控制的原理,先计算式(10)中电容电压的代价函数,从7个非直通矢量中选出2 个最优电压矢量,然后将这2 个电压矢量代入式(10)中输出电流的代价函数中计算得到1 个最优电压矢量,用于下一个控制周期。由此可见,S-MPC 可以消除MPC 中的权重系数。图3为qZSI 的S-MPC 策略整体控制框图。

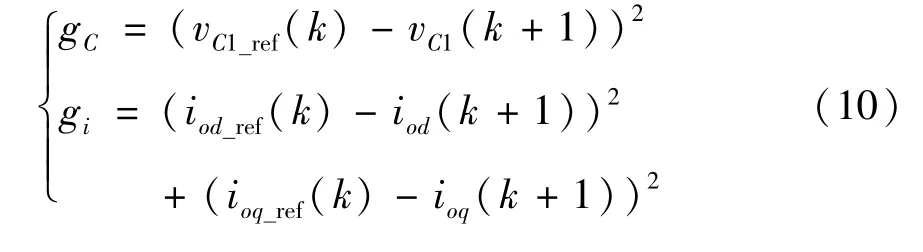
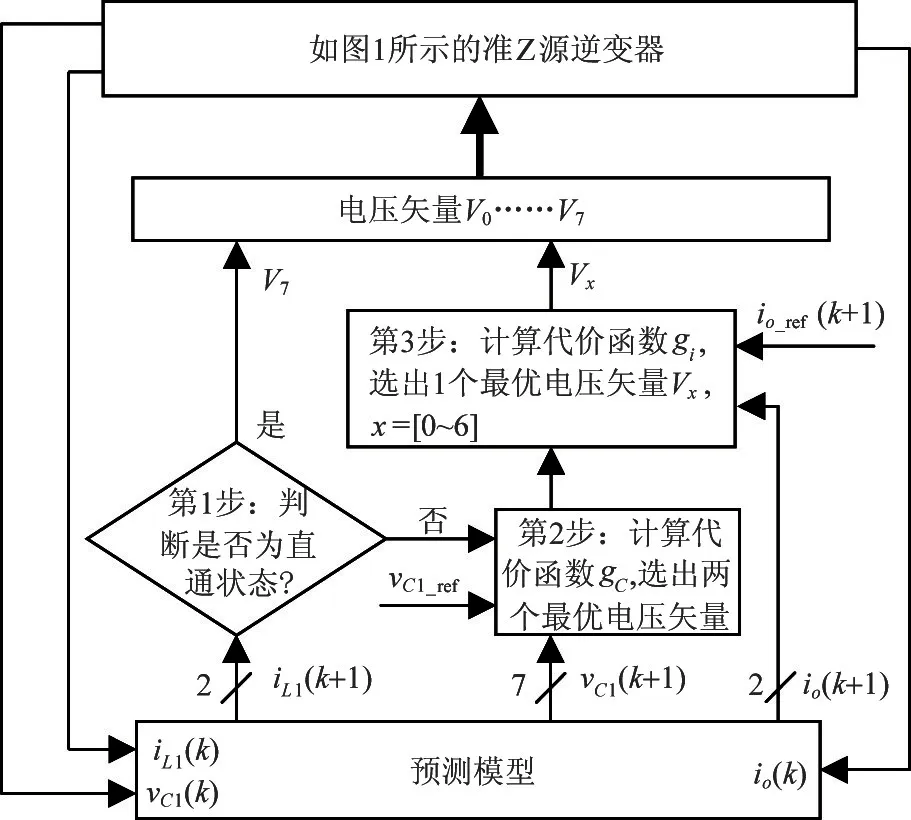
图3 qZSI 的S-MPC 策略整体控制框图

3.2 数字控制延时补偿

考虑到数字控制中存在大量的计算,计算所得的最优开关状态会在下一个控制周期中输出,而在这之前将继续使用前一个开关状态,这将导致系统输出延时,影响系统的控制性能。本文采用第(k+2)个采样时刻的预测值进行代价函数计算,以补偿输出延时。补偿方法如图4 所示。起始时采样tk时刻的系统变量x(k);在预测计算前,应用前一个控制周期tk+1计算得到的最优开关状态S(k);在当前开关状态S(k)的基础上,利用式(3)、(5)、(7)估算tk+1时刻的状态x(k+1);然后将该估算值作为起点,利用式(11)、(12)、(13)对tk+2时刻所有开关状态下预测值xp1(k+2)～xpn(k+2)进行计算。

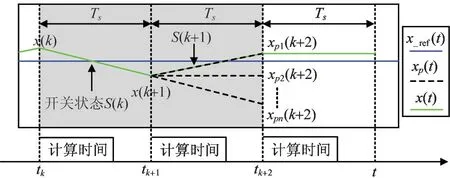
图4 延时补偿控制策略

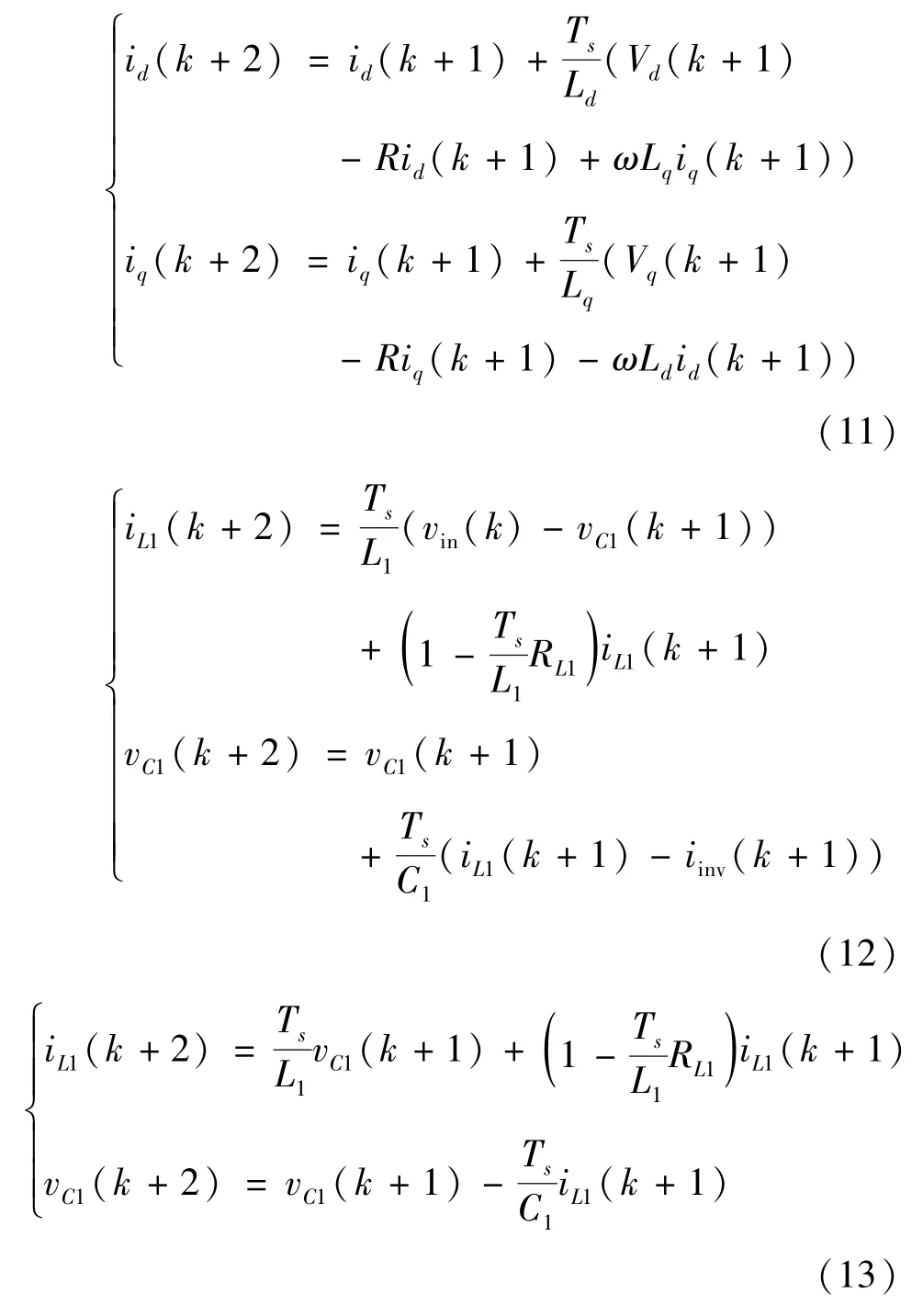
最后,根据代价函数式(15)计算下一控制周期的最优开关状态S(k+1),并在下一个控制周期tk+1开始时刻直接输出。另外为了进一步提高系统控制性能,利用矢量角补偿法来计算输出电流未来参考值,式(14)为计算输出电流未来参考值的公式[23]。

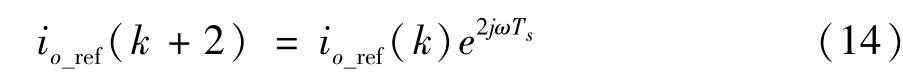
式中,io_ref(k)为当前时刻输出电流参考矢量,io_ref(k+2)为输出电流矢量的第(k+2)时刻参考值。

通过式(14)可计算第(k+2)时刻的d、q轴参考值iod_ref(k+2)、ioq_ref(k+2),将代价函数式(10)修改为

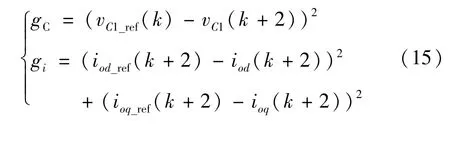
4 参数自适应模块及Lyapunov 证明

由于MPC 控制对控制量的预测,需要准确的电气参数信息。实际可能不方便获得准确的负载电气参数R和L,且实际运行过程中,电阻会随着温度上升而增加,电感会随着磁场饱和影响而下降。因此,设计对负载参数变化具有强鲁棒性的自适应的级联模型预测控制具有实际意义。

考虑到实际过程中电阻和电感值会发生变化,可假设电阻和电感模型为

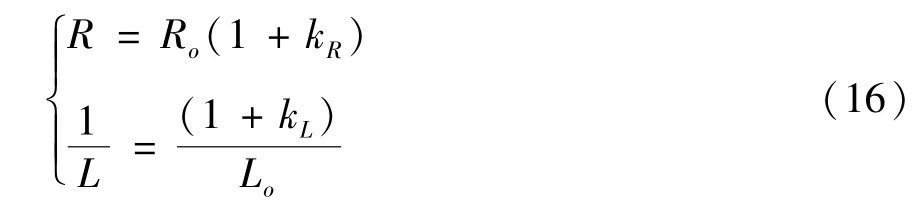
式中,Ro和Lo为MPC 算法中所使用的电阻和电感值,kR、kL分别为电阻和电感的误差系数。

将式(16)代入式(3)得电流真实值递推式:

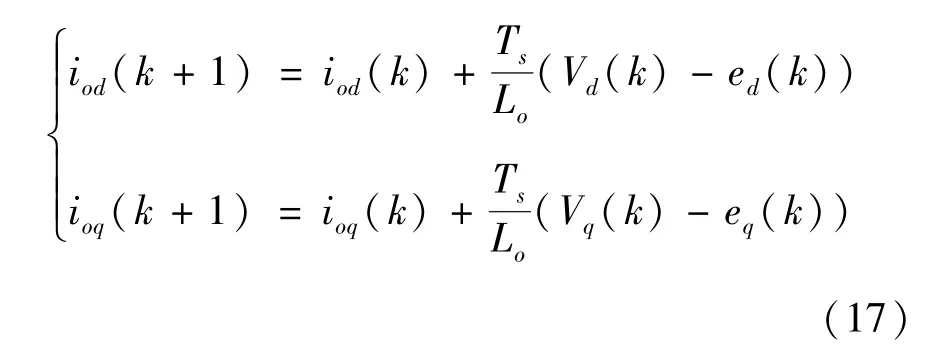
式中,ed(k)、eq(k) 为d、q轴上的总扰动,其表达式为

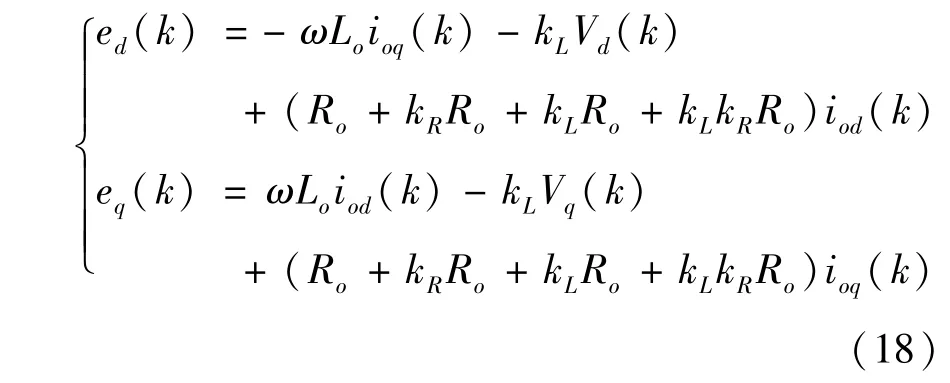
根据自适应控制的思想,可将式(3)的预测模型改为参数自适应预测模型:

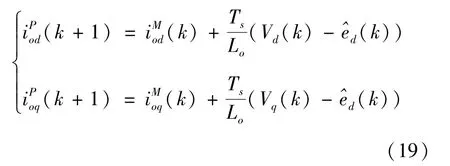
式中,上标P、M分别表示预测值和采样值,^表示估计值,设计d、q轴总扰动自适应律:

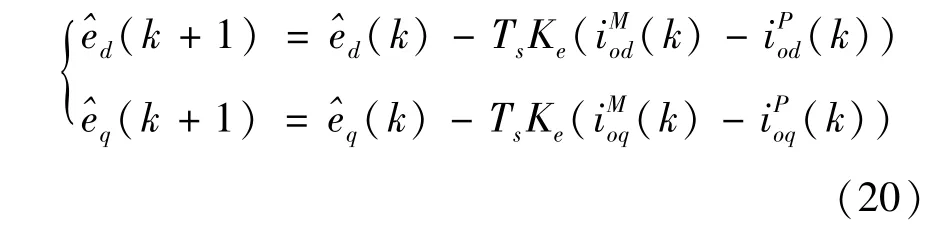
式中,Ke为估计器增益,为第(k-1)时刻输出电流预测值。

由式(19)、(20)可知,AS-MPC 不仅无需负载电阻信息,还可以对负载电感的误差做出补偿。

Lyapunov 稳定性证明定义总扰动估计的误差为

当系统处于稳态时,有ed、为常值,且分别收敛于Vd、Vq,因此可认为0、0。将误差项对时间求导并结合式(19)、(20),可得:

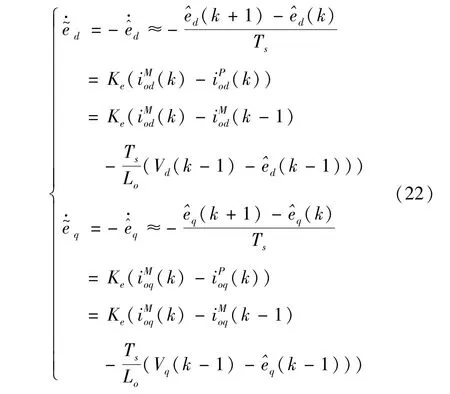
忽略电流采样误差,由式(17)可得:

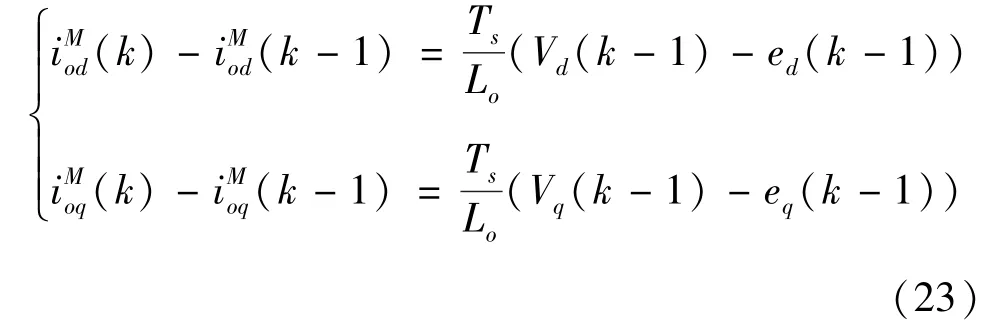
将式(23)代入式(22),并结合式(21)最终整理可得:

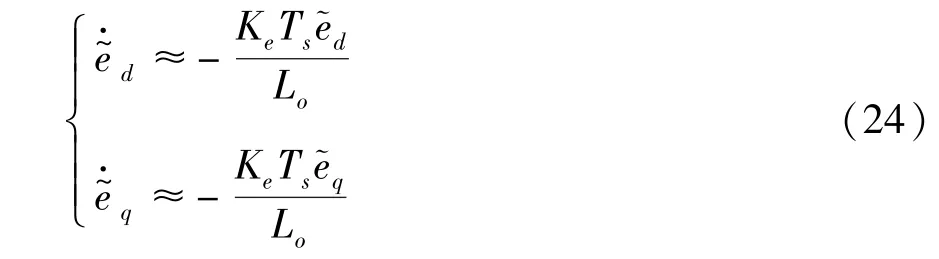
选取正定标量函数:

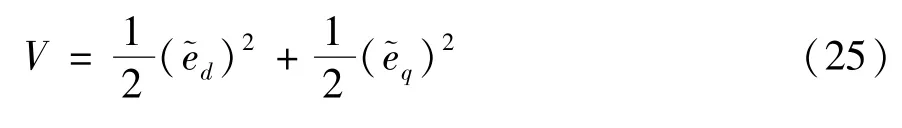
其对时间的导数为

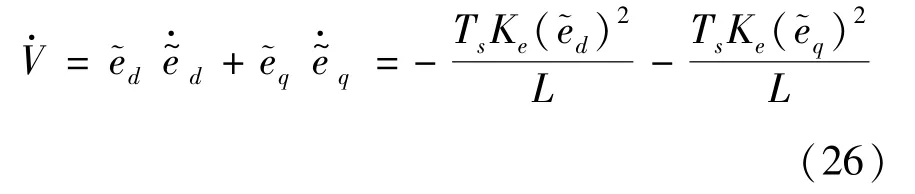
因为Lo、Ls、()2、()2均大于0,所以只要满足Ke大于0,则使负定。根据Lyapunov 稳定判据,总扰动估计值会渐进稳定。

5 实验结果

为验证本文提出的AS-MPC 策略有效性,搭建了如图5 所示的qZSI 的实验平台。

图5 样机实验平台

所搭建实验平台,功率管选用MOSFEST,型号为IRF640N,图1 阻抗网络中D选用肖特基二极管MBR10200,驱动芯片为 IR2110,控制芯片为TMS320F28335DSP。qZSI 系统主要参数见表2,系统输出电压频率为50 Hz。

表2 qZSI 系统实验参数

基于vin=30 V,Po_ref=60 W,vdc=40 V,由式(9)计算可得iL1_ref=2 A、Iom_ref=2 A、vC1_ref=35 V的条件下,比较S-MPC 和AS-MPC 两者控制性能。

5.1 延时补偿实验

在AS-MPC 策略下进行延时补偿对比实验,比较不加延时补偿与加延时补偿系统的性能,实验结果如图6 所示。由于电感电流在直通时上升斜率大,在非直通时下降斜率小,当未加延时补偿时,延迟一个采样周期输出开关状态会导致电感电流的纹波较大,且平均值明显超过了电感电流参考值,输出电流谐波也略大。通过延时补偿后,电感电流纹波减小且平均值与参考值更接近,输出电流的谐波也得到了改善。

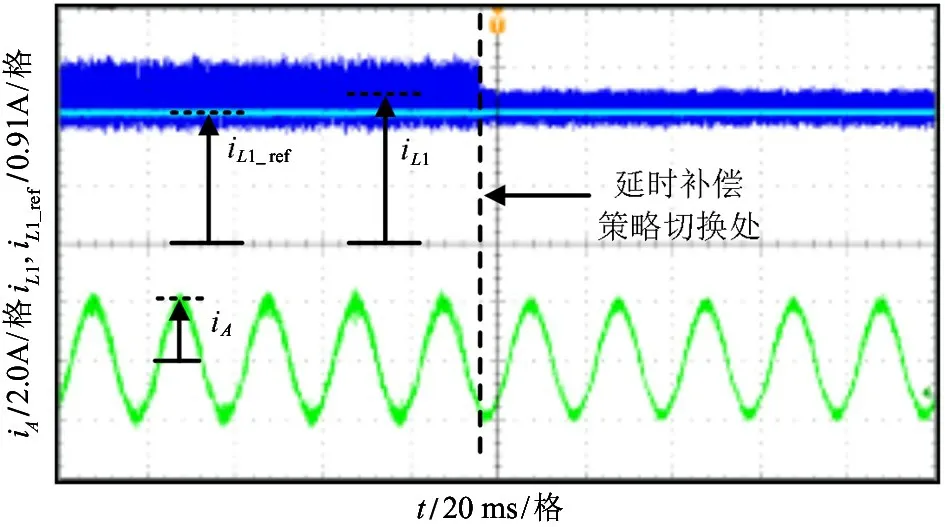
图6 在qZSI 系统中,AS-MPC 延时补偿实验结果

5.2 稳态性能实验

图7(a)和(b)分别为S-MPC 策略和AS-MPC策略的稳态性能实验对比,两者算法中所使用的电气参数一致,均为表2 中参数。由实验对比结果可知,两种控制策略的各个控制对象均得到了良好的控制。其中,S-MPC 策略的输出电流总谐波失真(total harmonic distortion,THD)为8.12%,AS-MPC策略的输出电流THD 为7.80%。由于本qZSI 系统中负载电感小,所以实验中输出电流THD 较高。

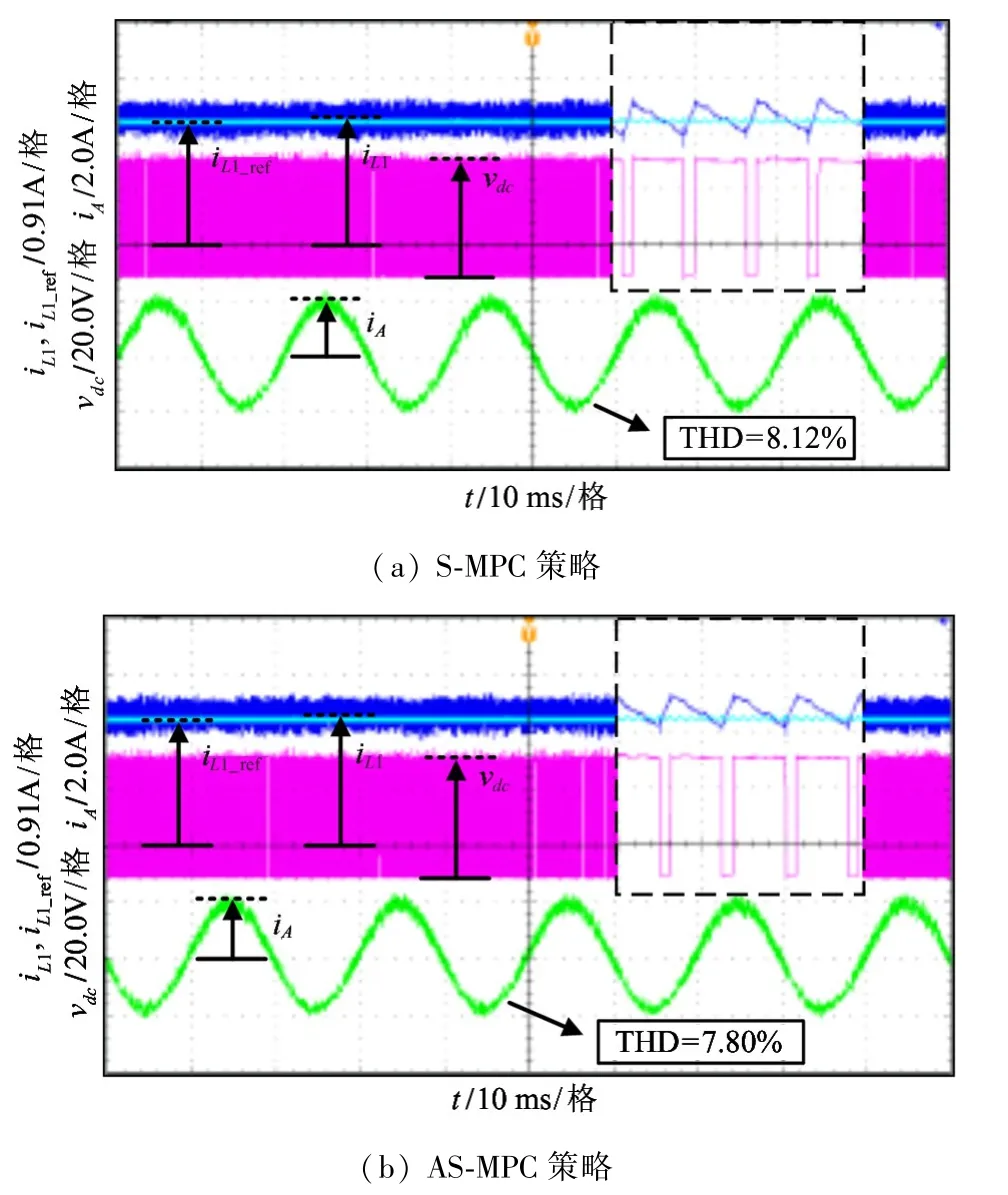
图7 S-MPC 和AS-MPC 稳态工作实验结果

本系统S-MPC 算法设计过程中未考虑参数误差和未建模动态误差,而在AS-MPC 策略中将所有未知信息当作总扰动。因此,AS-MPC 具有更优异的稳态控制性能。

5.3 动态性能实验

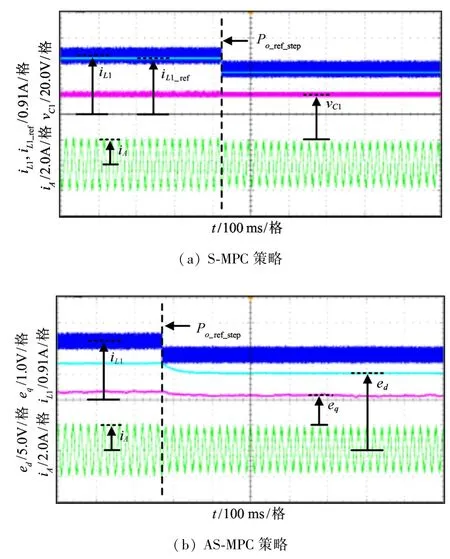
图8 S-MPC 和AS-MPC 动态实验,输出功率从60 W 阶跃至45 W 实验结果

5.4 参数自适应对比实验

为验证AS-MPC 策略的参数鲁棒性,设计了电阻、电感参数不匹配实验。

5.4.1 负载电阻R的参数自适应对比实验

考虑到在实际运行中,电阻会随着温度改变而发生变化。为模拟电阻不匹配现象,在S-MPC 的DSP 程序中,设置Ro=20 Ω 为实际电阻2 倍,Lo=3 mH。然而,AS-MPC 实现中,电阻相关项被当做综合扰动,无需电阻参数,因此两种控制策略实验对比如图9(a)和(b)所示。虽然两种控制策略都能实现对输入电流、电容电压和输出电流的稳定控制,但是,S-MPC 控制输出电流THD 为9.32%,而AS-MPC控制输出电流THD 为7.80%。由此可见,相比SMPC,AS-MPC 方法无需电阻参数,同时对电阻摄动具有强鲁棒性。

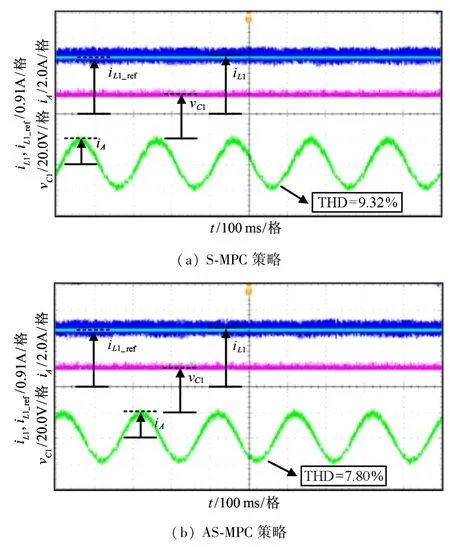
图9 Ro=20 Ω 条件下S-MPC 和AS-MPC 的实验结果

5.4.2 负载电感L的参数自适应对比实验

在实际的工作过程中,不仅负载电阻会发生变化,负载电感也会随着磁场饱和程度不同而改变。在S-MPC 和AS-MPC 算法中,设置Ro=10 Ω,Lo=2 mH,其余条件一致,比较两者控制性能,实验结果如图10(a)和(b)所示。由图10 可知,当电感参数与实际参数不匹配时,两种控制策略均能实现输入电流、电容电压和输出电流的稳定控制。但是,图10(a)中采用S-MPC 策略,输出相电流的THD 为8.57%;图10(b)为采用AS-MPC 策略,输出相电流的THD 为8.21%。由此可知,相比S-MPC 策略,AS-MPC 策略对负载电感的摄动同样具有较强的鲁棒性。

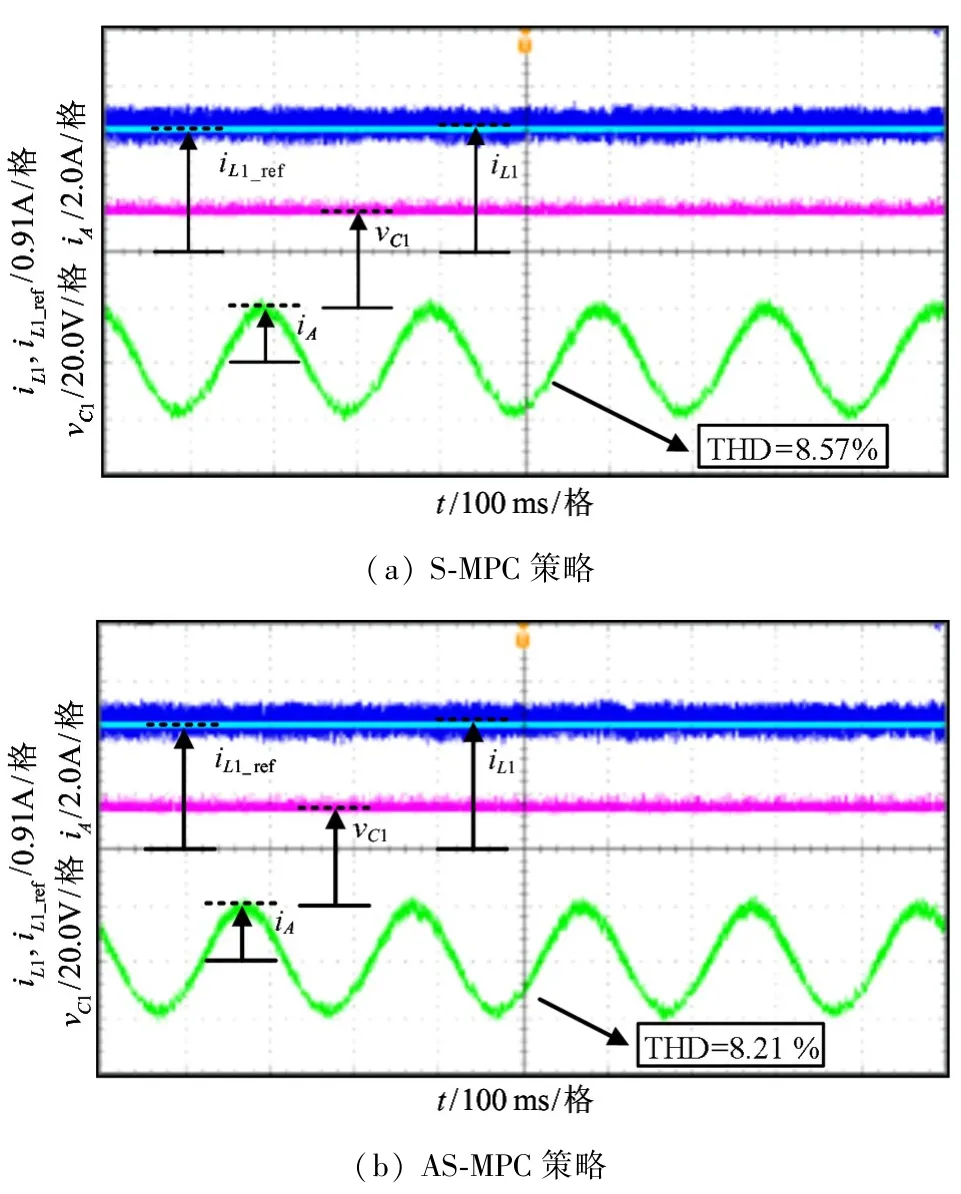
图10 Lo=2 mH 条件下S-MPC 和AS-MPC 的实验结果

6 结论

针对传统FCS-MPC 策略需要设计权重系数的问题以及控制性能依赖于精确模型参数的缺点,本文提出一种适用于qZSI 的AS-MPC 策略。通过被控对象的优先级,依次计算各自对应的代价函数,并将参数误差当作总扰动,采用自适应方法进行估计,从而消除了权重系数并实现对负载电气参数摄动具有强鲁棒性。同时,考虑AS-MPC 数字控制系统存在输出延时以及参考指令滞后的问题,给出延时补偿方法和矢量角参考指令补偿方法。实验结果表明,所提出的AS-MPC 策略具有无权重系数、结构简单、对参数摄动鲁棒性强、输出电流谐波低、动态响应快速等特点。