CFBB 燃烧过程变经济性能多目标预测控制①

何德峰 李海平 王青松 李廉明

(*浙江工业大学信息工程学院 杭州310023)

(**嘉兴新嘉爱斯热电有限公司 嘉兴314016)

0 引言

循环流化床锅炉(circulation fluidized bed boiler,CFBB)是一种靠燃料燃烧生产蒸汽的动力装备,相比于普通煤粉锅炉具有适用燃料种类多、燃烧效率高和污染排放量少等优势[1-4]。特别是近年来,以农作物秸秆为燃料的生物质循环流化床锅炉的兴起,在提高废弃资源利用率的同时,降低了企业成本和环境污染,因此CFBB 在电力、化工及供热等领域受到广泛推广和应用。然而,同普通煤粉锅炉相比,CFBB 燃烧反应机理更复杂,既要满足热负荷需要,又要保证锅炉在稳态工况长期运行和燃烧的经济性等诸多条件。随着CFBB 技术日益大型化和参数化,其复杂的过程控制和以节能减排为主的多目标优化控制问题越来越受到关注,并日益成为热电控制领域的热点课题[5-6]。

国内外学者针对CFBB 燃烧过程优化和节能降耗问题已经开展了大量工作,一些先进优化控制算法不断被应用。考虑到CFBB 过程的时变、强耦合特性,文献[7]提出一种基于改进遗传算法的循环流化床锅炉床温模糊控制器,能够有效地对锅炉床温进行调节。文献[8]先采用自适应神经模糊推理系统建立CFBB 过程模型,再通过强化学习算法进行控制优化,能够有效提高锅炉的燃烧效率。模型预测控制(model predictive control,MPC)作为一种能够处理目标优化和约束问题的先进控制算法,广泛应用于工业过程控制[9]。文献[10]考虑风煤比对燃烧过程的影响,提出一种基于模型预测控制的循环流化床锅炉燃烧优化方法,并与传统PID 控制方法进行对比仿真表明所提方法的有效性。针对CFBB 燃烧过程中的多目标优化问题,文献[11]以提高燃烧效率和减少污染物排放量为优化目标,利用支持向量机构建CFBB 燃烧过程模型,设计非线性MPC 算法,实现了燃烧过程的多目标优化控制。

随着实际需求的提升,如何在保证锅炉燃烧效率的同时提高经济效益也越来越受到关注。文献[12]提出一种基于广义预测控制的CFBB 燃烧过程多目标经济优化策略,实现了锅炉主要工艺参数的区域动态控制和经济性能指标优化。文献[13]考虑锅炉燃烧过程中主要工艺参数的平稳性和经济性问题,提出了一种基于模型预测控制的双层控制策略,在保证工艺参数的稳定性的基础上进行第二层的经济性能指标优化,实际测试结果表明该策略能提高经济性能。文献[14]提出了一种CFBB 燃烧过程多目标优化方法,应用终端约束集、终端代价函数和局部控制器三要素设计多目标模型预测控制器,保证了系统在最优经济平衡点(稳态工况)处的稳定性。然而上述涉及到经济性能优化的研究工作均没有考虑经济性能指标可变这一关键问题。经济性能指标改变意味着系统稳态工况的改变,因此如何设计控制器保证CFBB 燃烧系统在经济性能指标改变后在新的稳态工况长期稳定运行是一个新的研究方向。

本文考虑在经济性能指标可变情况下循环流化床锅炉燃烧过程的多目标优化控制问题。引入关于最优经济稳态点的正定辅助函数作为最高优先级目标,再考虑床温设定值跟踪目标和经济目标,构建多层字典序优化控制结构,实现了变经济性能情况下CFBB 燃烧过程的稳定运行和经济性。在文献[14]工作的基础上,结合广义终端约束、字典序多目标优化和滚动时域控制原理,设计循环流化床锅炉燃烧系统变经济性能多目标模型预测控制器。

相比文献[14],本文做出的改进体现在两个方面:(1)考虑可变的经济性能指标,这意味着燃烧过程的最优经济稳态点会发生改变,因此如何保证循环流化床锅炉在最优经济稳定工况下稳定运行是本文在设计控制器时解决的主要问题;(2)设计控制器时引入广义终端约束和关于最优经济稳态点的正定跟踪辅助目标函数,能够保证在经济最优稳态点发生改变后控制器的可行性和闭环系统的稳定性。

1 CFBB 燃烧过程描述与建模

1.1 CFBB 燃烧过程描述

CFBB 燃烧系统装置主要组成部分包括炉膛、分离器、过热器、省煤器、返料器和除尘器等。CFBB燃烧过程可简述为[15]:生物质燃料和脱硫剂的混合物进入炉膛后,在流化状加热物料的加热作用下燃烧,同时一、二次风机分别向炉膛鼓入一次风和二次风供给燃料燃烧;在上升气流的作用下,燃料向炉膛上部运动,粗燃料颗粒被带入炉膛密相区燃烧,细颗粒随烟气在稀相区悬浮燃烧。部分被夹带出的细颗粒在分离器作用下进入返料器,然后被送回炉膛循环进行二次燃烧利用。烟气通过过热器与尾部的受热面完成热交换后经除尘器净化处理排出。整个燃烧过程产生的热量被热交换器捕获用于发电和供热等。

1.2 CFBB 燃烧过程建模

CFBB 燃烧系统建模方法分为两种:一种是根据实际测量得到的输入输出数据,经系统辨识[16]或学习[17]方法得到;另一种是通过描述CFBB 燃烧过程中的传质、传热和燃烧等物理和化学过程,结合质量和能量守恒定律建立的机理模型。本文考虑机理建模。

燃料的燃烧速率QB主要取决于炉膛内的氧含量和燃料特性,具体计算如下:

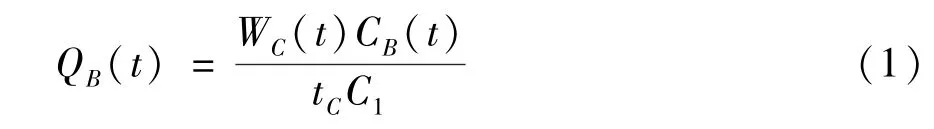
式中,WC为炉膛内燃料剩余量,CB和C1分别为炉膛和一次风中的氧气含量,tC表示燃料的平均燃烧时间。由质量守恒定律可以得到炉膛内燃料剩余量的变化为

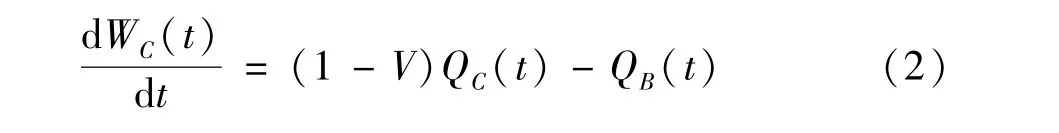
式中,V为燃料挥发比,QC为燃料供给速率。

炉膛内氧气含量是保证燃烧效率的关键指标,其主要取决于一次风中的氧含量和燃料耗氧量。炉膛氧含量和稀相区氧含量CF的动态变化可以分别表示为

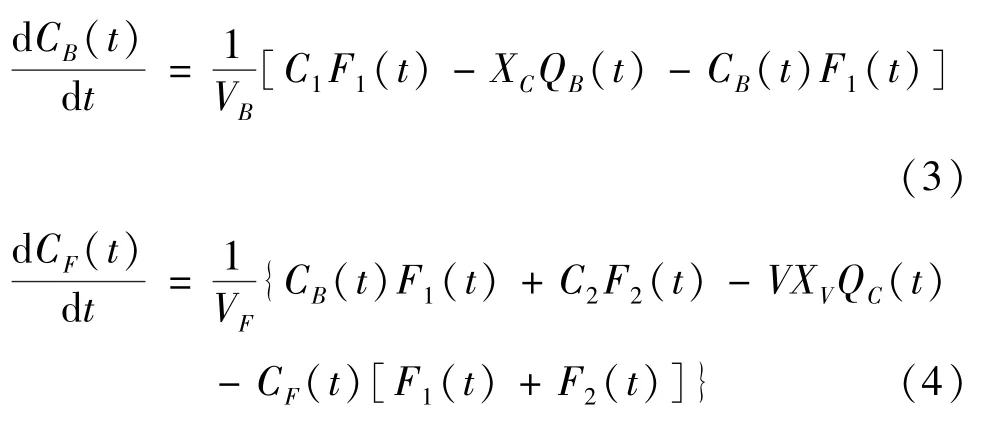
式中,VB和VF分别为炉膛和稀相区的体积,F1和F2分别为一和二次风的供给速率,C2为二次风中的氧气含量,XC和XV分别为燃料和燃料中挥发物的耗氧系数。

床温和稀相区温度是保证燃料燃烧效率的关键工艺参数,根据CFBB 燃烧过程中的热量转化和能量守恒定律可以得到炉床温度TB和稀相区温度TF的平衡关系分别为

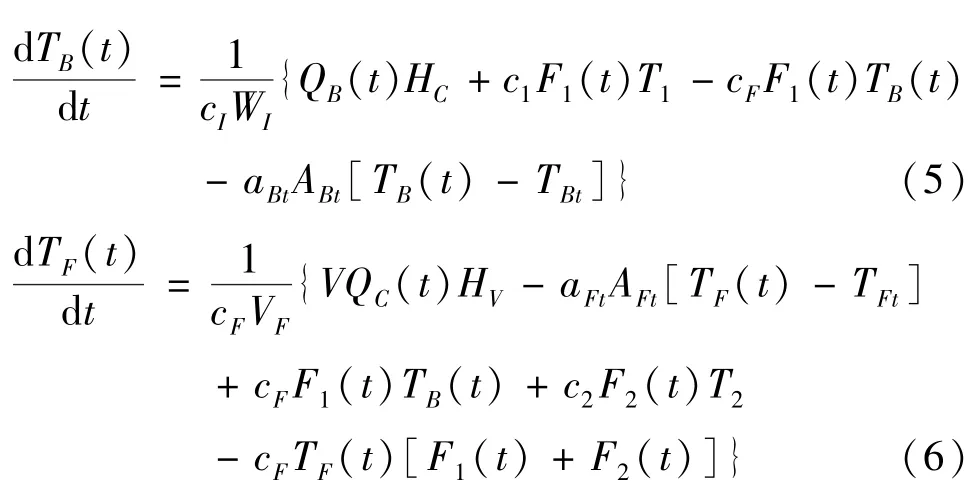
式中,cI和WI分别为炉床材料的比热系数和质量,HC和HV分别为燃料和燃料中挥发物的比热,c1和T1分别为一次风的比热系数和进风温度,aBt和ABt表示炉床水冷壁的传热系数和炉床水冷壁面积,TBt为炉床冷水的温度,cF表示烟气的比热,aFt和AFt表示稀相区水冷壁的传热系数和稀相区炉床水冷壁面积,TFt为稀相区冷水的温度,c1和T1分别为一次风的比热系数和进风温度。

此外,CFBB 燃烧过程的热功率PT可以采用简单的一阶动态模型表示为

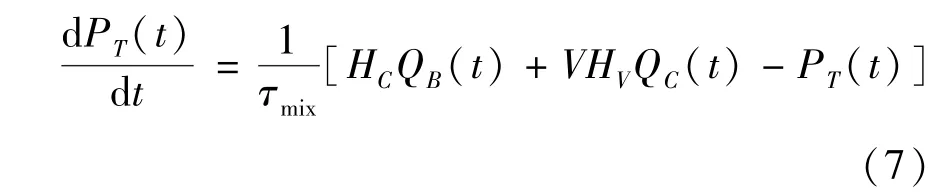
其中,τmix为时间常数。

结合式(1)～式(7),选取CFBB 燃烧过程的状态变量为x=[WC,CB,CF,TB,TF,PT]T和控制输入变量u=[QC,F1,F2]T,可以得到CFBB 燃烧过程的连续时间系统模型:

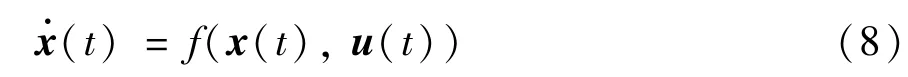
为了便于控制器设计,以采样时间Ts对连续系统式(8)进行离散化处理得到离散时间的CFBB 系统模型。

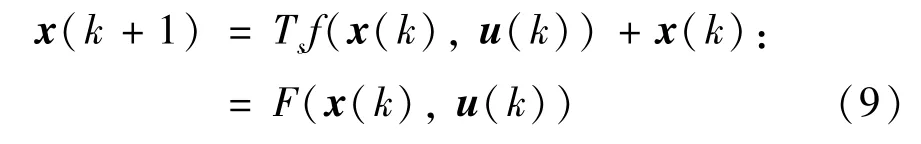
为了提高燃烧效率、保证系统安全稳定运行以及燃烧过程的环保性,系统的状态量和控制量要满足如下约束条件:

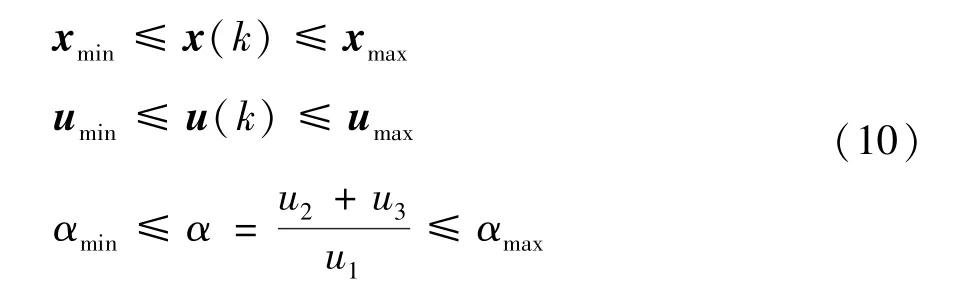
式中,一般符号smin和smax分别表示对应物理量约束的上和下限;α为风煤比,保证其在合理范围内能最大限度减小氮氧化物的排放,提高燃烧过程的环保性。

2 CFBB 燃烧过程多目标描述

CFBB 燃烧过程中的主要控制目标可以归纳为以下3 个方面。

(1) 稳定运行目标。要保证CFBB 燃烧过程的稳定和经济性运行,防止系统状态偏离预期稳态工况,造成不稳定和安全问题,需要控制系统状态量和控制量在某些经济稳态平衡点。设计稳态跟踪目标函数为

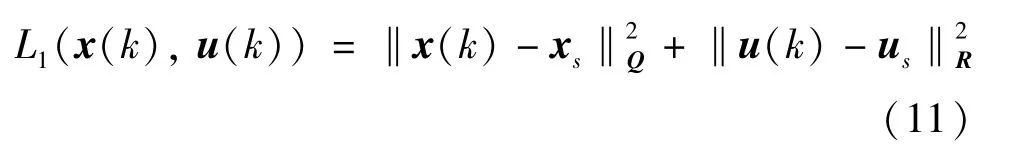
式中,xs和us分别表示CFBB 锅炉燃烧过程的经济最优稳定状态和控制输入,Q、R分别为状态量偏差和控制输入偏差的正定加权矩阵,一般性矩阵ψ加权范数。

(2) 床温控制目标。炉床温度TB是一个关键性参数,直接影响到燃料燃烧效率和机组的经济安全运行。通常保证锅炉运行的炉床温度需要控制在1073.15～1173.15 K 范围内的某些期望值。因此,设计炉床温度期望值跟踪控制目标函数如下:

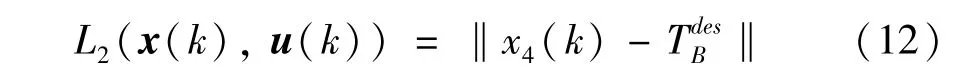
其中,为锅炉燃烧过程中期望的床温。(3) 经济性目标。CFBB 燃烧过程的能耗主要来自于燃料的消耗量,燃料传输装置的耗电量和风机的送风耗电量。而传输装置的耗电量与风机耗电量量级相差很大,因此前者可忽略不计[12-13]。本文的经济成本主要考虑燃料消耗量、一次风机耗电量和二次风机耗电量。参考文献[16]的方法,结合一、二次风机的实际送风速率和燃料消耗之间的关系,经济性能目标函数可以折算为系统每秒的燃料消耗量,具体如下:

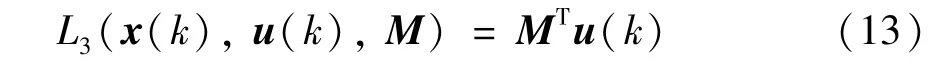
其中,M=[m1,m2,m3]T为经济折算系数。考虑燃料价格发生改变或者由于峰谷电等因素导致电价发生变化等因素,M会发生改变,即经济性能指标是可变的。

考虑上述3 个控制目标,CFBB 燃烧过程的多目标模型预测控制问题可以描述为

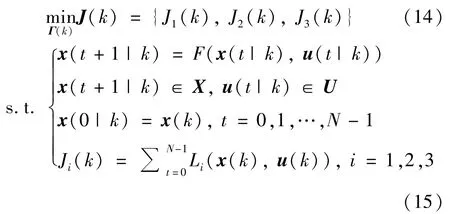
式中,s.t.表示约束,k为当前采样时刻,N为预测时域,一般符号s(t|k)表示当前k时刻对未来k+t时刻的预测值,X⊆R6和U⊆R3分别表示状态量和控制量约束集合。注意多目标优化问题式(14)的最优解是定义在Pareto 最优性意义下的,通常Pareto最优解不唯一,它们共同构成了多目标值域空间的Pareto 前沿。令当前时刻的一个Pareto 优化控制解序列Γ(k)为

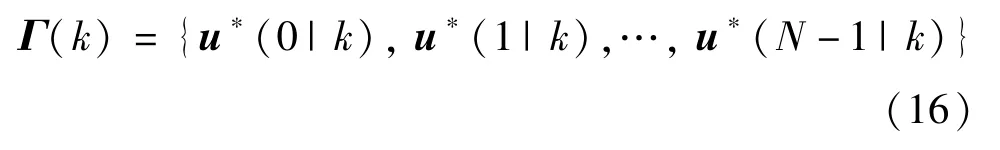
极小化每个目标函数,若优化问题式(14)可行,即序列式(16)存在,则由MPC 滚动时域原理可以得到预测控制器为

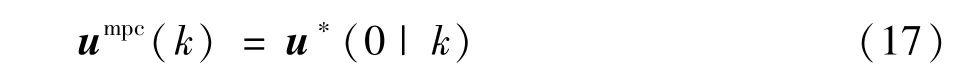
其中,u*(0|k)为序列式(16)的第一个元素。

传统的保证系统在最优经济平衡点处渐近稳定性的控制器设计依赖于终端三要素条件,即终端代价函数、终端约束集和终端局部状态反馈控制器[18]。在每次优化过程中,通过终端局部状态反馈控制器将系统的终端状态x(N|k)驱使到终端约束集内,结合Laypunov 稳定性理论可以保证系统在平衡点的渐近稳定性。终端三要素条件需要根据给定的系统稳态点离线计算,然后用于控制器设计,相关设计方法见文献[14]。然而当经济性能指标式(12)变化时系统的最优经济稳态点随之改变。这意味着保证系统稳定性的终端三要素条件不再适用于新的稳态点,导致控制器的可行性和稳定性丢失。

本文旨在设计一种经济性能可变的CFBB 燃烧过程多目标模型预测控制算法,在由于燃料价格发生改变或者由于峰谷电等因素导致经济性能指标发生改变的情况下,保证控制器的可行性和稳定性,进而实现CFBB 燃烧系统在不同稳态工况下长期稳定运行和经济性运行。

3 变经济性能Mo-MPC 控制器设计

通常,控制目标J1～J3具有矛盾冲突性和不同优先级,字典序优化方法是处理优先级多目标问题的有效方法之一[19-22]。本文主要基于字典序多目标优化方法设计控制器。

首先定义CFBB 燃烧过程的最优经济稳态点考虑CFBB 燃烧系统式(9)中各状态变量之间的平衡关系和主要目标控制要求,燃烧系统的最优经济平衡点可以通过求解以下优化问题:

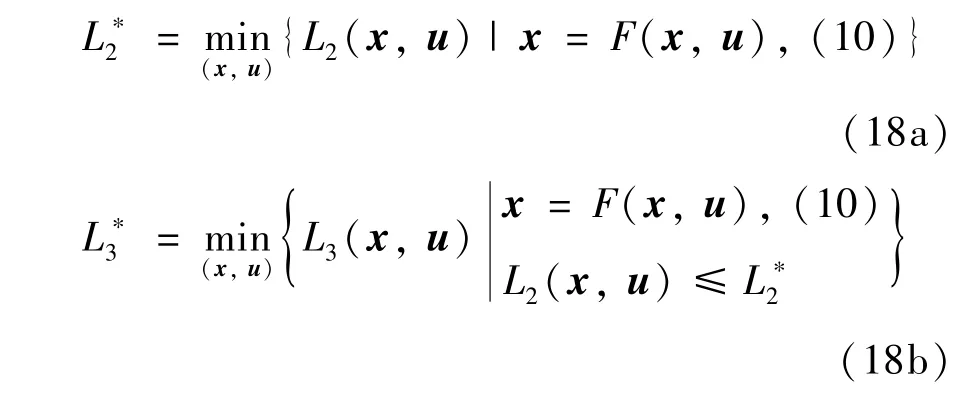
得到CFBB 燃烧过程的最优经济稳态点为

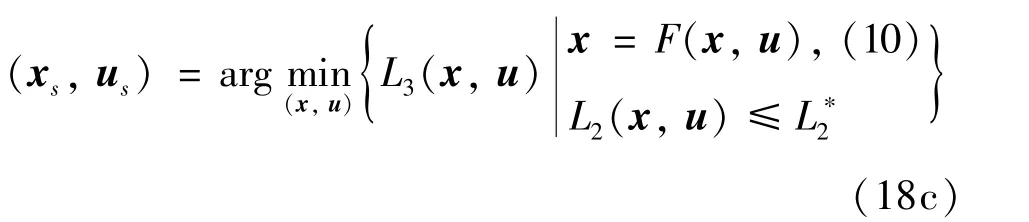
为了提高字典序优化的计算效率,常规字典序约束Li=通常被松弛为Li≤+εi,εi≥0 为小的常数松弛因子,在上述稳态优化和后续的字典序优化过程中的字典序约束已简记为Li≤。由式(18b)可知,稳态点优化求解依赖折算系数M,当M变化时,CFBB 燃烧过程的稳态工况随之改变,导致基于终端三要素的设计的控制器的可行性和系统稳定性丢失。因此本文在控制器设计时,考虑广义终端约束[23],即x(N-1|k)=x(N|k)。定义燃烧过程的可行控制输入集如下:

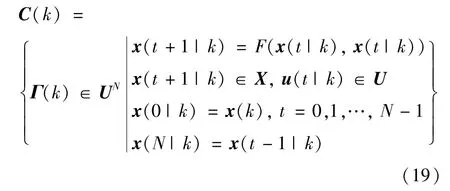
式中,UN表示N与集合U的乘积。

重新设计稳态跟踪目标函数为

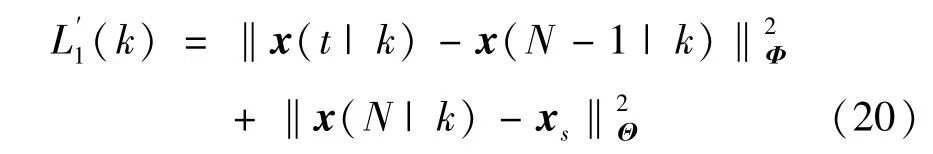
其中,Φ和Θ均为正定矩阵。基于字典序优化方法,CFBB 燃烧过程可变经济性能Mo-MPC 优化控制策略,描述如下:

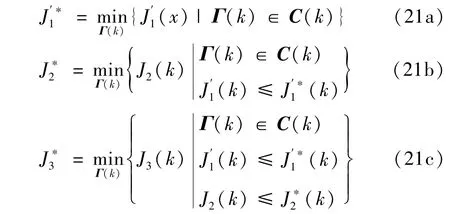
其中,(i=1,2,3)表示目标函数的最优值函数。根据字典序优化原理,上述优化策略得到的字典序最优解为

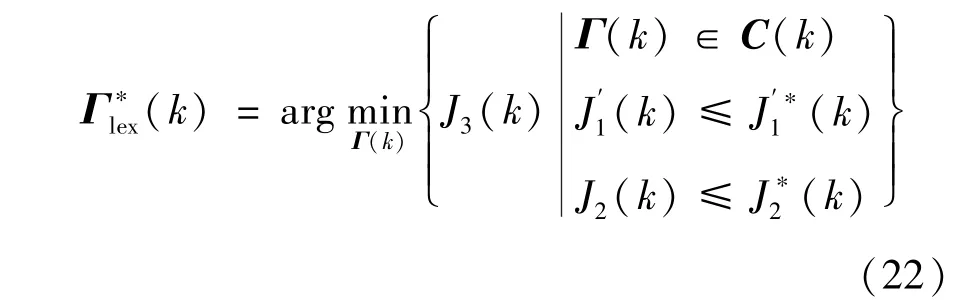
由字典序最优解[24]的定义可知,字典序最优解序列式(22)本质上是一个考虑了各目标优先级的Pareto最优解,它可能是不唯一的,但目标最优值是Pareto前沿上的唯一点。

根据MPC 滚动优化原理,变经济性能Mo-MPC控制器设计为

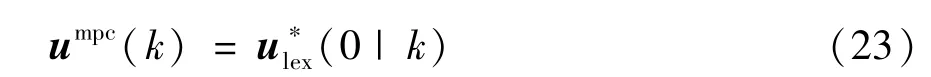
其中,(0|k)为字典序最优控制序列式(22)的第一个元素,得到对应的CFBB 燃烧过程的闭环控制系统:

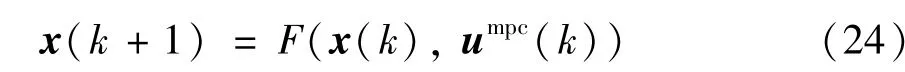
由上,CFBB 燃烧过程变经济性能Mo-MPC 控制算法归纳如下。

步骤1设定参数(N,Φ,Θ);令k=0。

步骤2判断当前时刻M是否需要调整,如是,求解问题式(18)得到对应的(xs,us),并更新目标函数和J3;否则转步骤3。

步骤3测量当前状态x(k),按如下步骤进行字典序优化问题求解:

步骤3.1求解第一层优化问题式(21a),得到控制序列(k);

步骤3.2求解优第二层优化问题式(21b),得到控制序列(k);

步骤3.3求解优化问题式(21c),得到控制序列(k);

步骤3.4确定Mo-MPC 优化问题式(21)的字典序最优解序列,。

步骤4将((k)的首个元素作用于CFBB 燃烧实际系统式(9)。

步骤5令k=k+1,返回步骤2。

得到的CFBB 燃烧系统变经济性Mo-MPC 控制器结构如图1 所示。

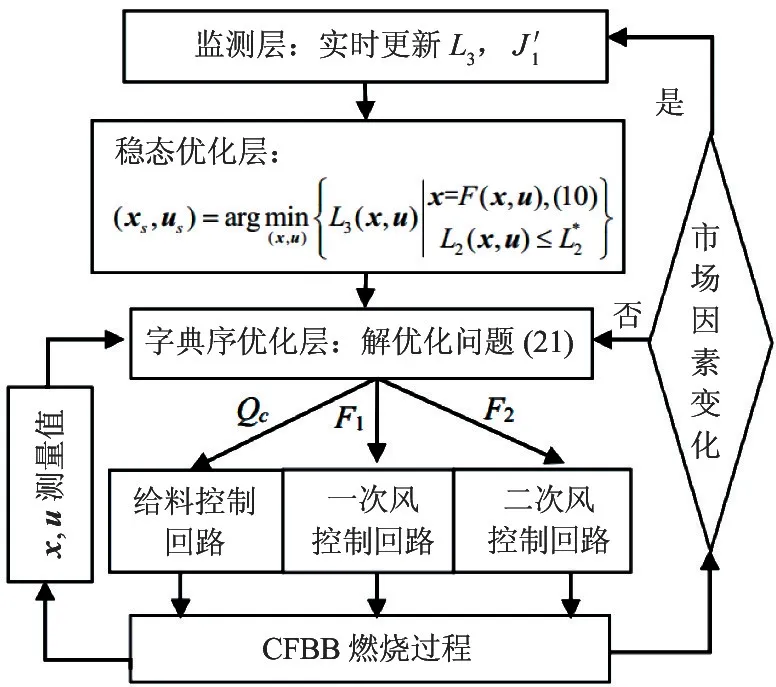
图1 变经济性能Mo-MPC 控制器结构示意图

4 仿真结果与分析

采用文献[25]中的CFBB 燃烧系统模型,模型参数见表1。

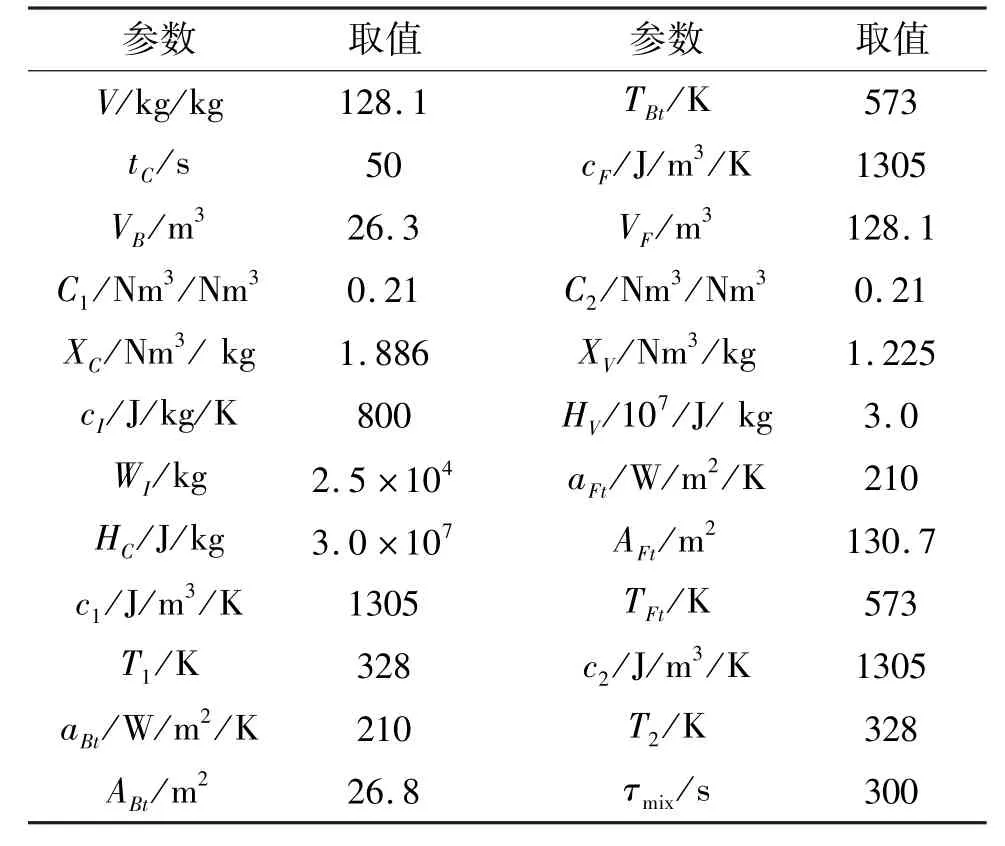
表1 CFBB 模型参数取值

以采样时间Ts=1 s 对连续时间系统式(8)进行离散化处理;预测时域N=8;中的正定加权矩阵Φ(diag{5,20,20,10,10,5},Θ(diag{25,25,25,25,25,25};锅炉燃烧过程中床温设定值为1117.0 K;考虑CFBB 燃烧过程的安全、稳定和经济性,需对锅炉的状态量和控制量施加约束,炉膛内燃料剩余量WC需要控制在221～223 kg 范围内,炉膛内氧含量CB和稀相区氧含量CF均应保持在0.03～0.06 Nm3/Nm3范围内;炉床和稀相区温度TB、TF分别应控制在1169.8～1171.2 K 和998.5～1004.5 K 范围内;热功率P的约束为32～33 MW;同时控制输入应满足约束条件,供给燃料速率QC限制在3.5～4.5 kg/s范围内;一次风机的鼓风速率限制在4.0～6.0 Nm3/s 之间;二次风机的鼓风速率须在14.0～16.0 Nm3/s 范围内;为了尽可能减少氮氧化物NOx的生成量,风煤比须控制在4.0～6.0 范围内。仿真时间为Tsim=1600 s;在800 s 时经济性能指标发生改变,经济折算系数和对应的CFBB 系统稳态工况见表2。

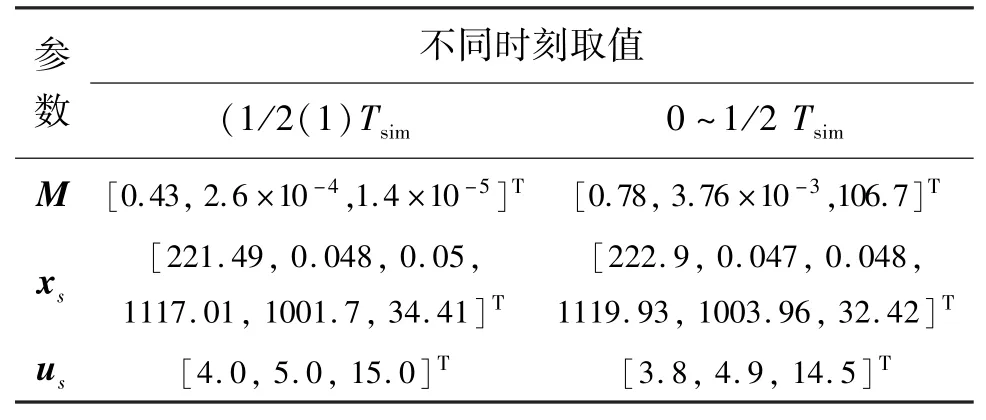
表2 燃烧过程的不同稳态工况

仿真中取CFBB 燃烧系统的初始状态x(0)=[222.5,0.05,0.055,1116.95,1003.78,32.446]T,分别运行本文的算法A 和文献[14]中的算法B,其中运行算法B 时的终端三要素条件与文献[14]相同。图2 和图3 分别给出了两种控制器控制下的CFBB 燃烧系统的6 个状态量变化响应曲线和控制量变化响应曲线。图中,实线对应的是运行算法A得到的响应曲线,虚线对应的是运行算法B 得到的响应曲线。

由图2 和图3 可以看出,2 种算法运行得到的状态量和控制量均满足约束条件。在稳态工况发生改变之前,在算法A 的控制作用下,大约200 s 后CFBB 燃烧系统基本能够稳定到稳态工况,且均能保证锅炉的炉床温达到设定值;在算法B 作用下,大约180 s 后燃烧过程也能达到稳态工况,但是部分状态量和控制量出现明显的波动,控制的平稳性较差。当经济指标发生改变导致稳态工况改变后,本文设计的控制器仍然能够保证CFBB 燃烧系统在新的稳态工况稳定运行,床温基本能稳定在期望值附近。但在控制器B 的控制作用下锅炉的各状态量出现明显的抖动,不能保证新的稳态工况下锅炉的稳定运行要求,并且床温也无法稳定在期望值。这主要是因为在经济性能指标发生改变后,新的最优经济稳态点不满足保证算法B 稳定运行的终端三要素条件。

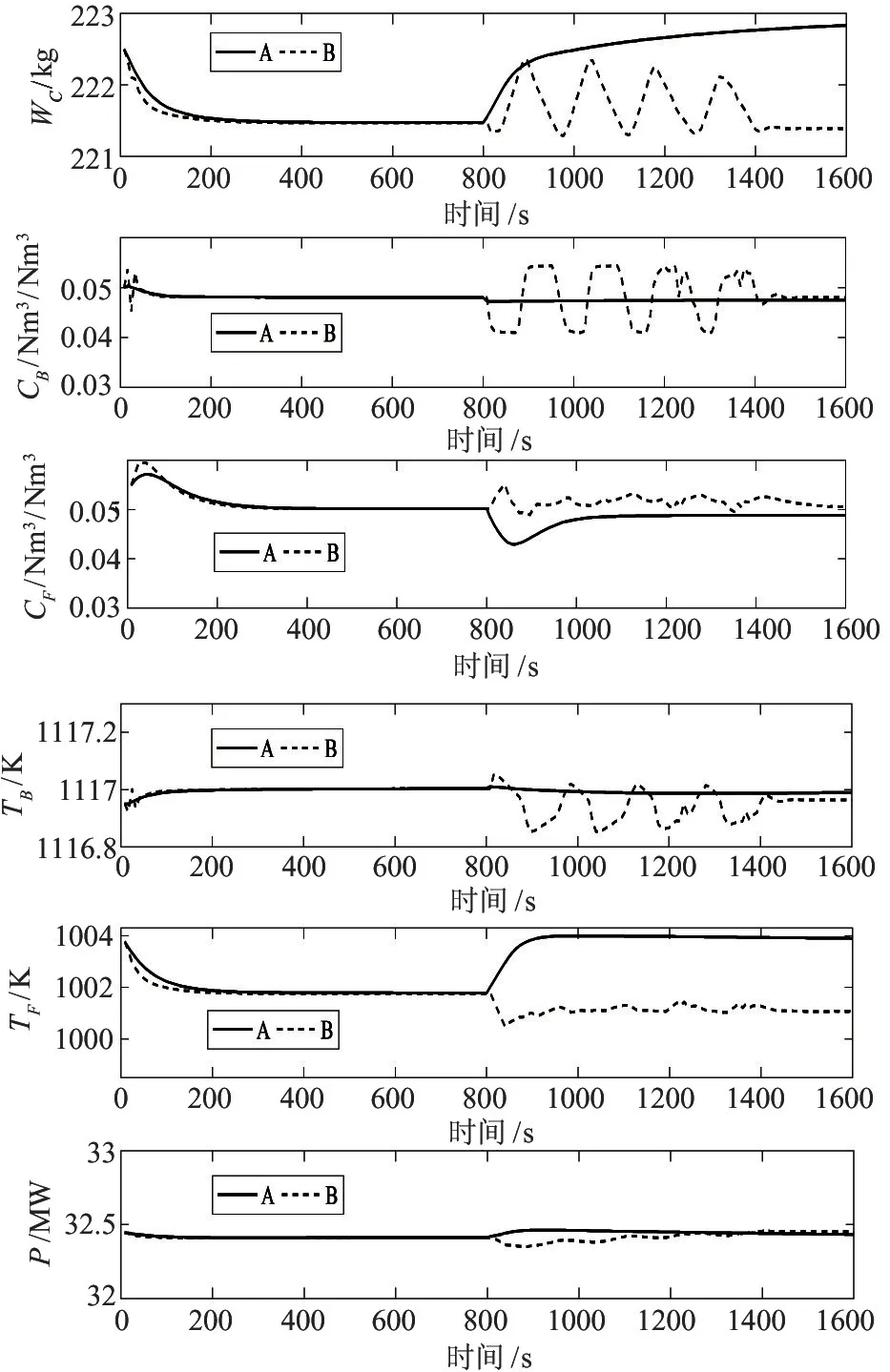
图2 状态量响应曲线

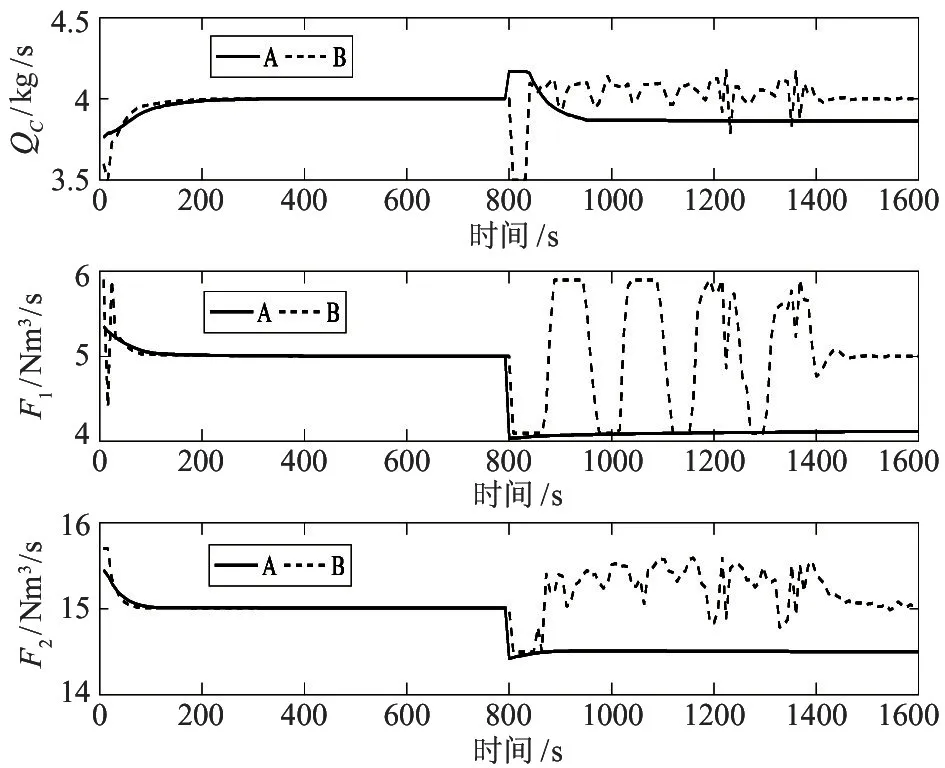
图3 控制量响应曲线

图4 给出的是2 种算法运行后CFBB 燃烧过程中的风煤比变化情况。由图可知,两种控制器作用下系统均满足风煤比约束,但当经济性能指标发生变化后,控制器B 作用下燃烧系统的风煤比出现波动,这意味着燃料不充分燃烧,导致生成的NOx增加,不利于提高锅炉燃烧的环保性。因此,本文提出的算法控制作用下风煤比能稳定在一个合理取值,更利于燃料的充分燃烧,更符合环保性控制要求。

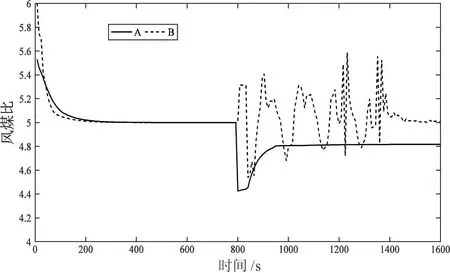
图4 2 种算法控制下的风煤比

以闭环系统的平均经济性能衡量两种控制器作用下系统的经济性能,平均经济性能表示为

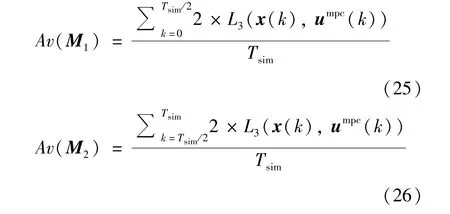
两种控制策略下CFBB 燃烧过的平均经济性能见表3。

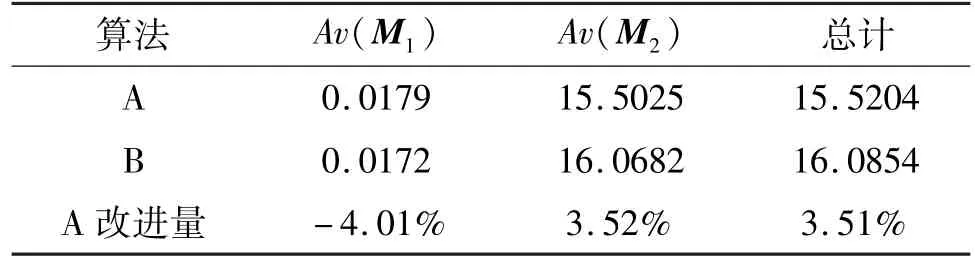
表3 2 种算法的平均经济性能

由表3 结果可知,0～800 s 时间范围内,本文提出的算法相比较于算法B 改进平均经济性能-4.01%;800～1600 s 时间范围内,本文提出的算法相比较于算法B 改进3.52%;整个仿真时长内本文算法改进3.51%。整体而言,本文提出的算法在提高燃烧经济性方面优于算法B。

总之,相比于算法B,本文提出的算法既能够保证CFBB 燃烧系统在不同稳态工况下的稳定运行,又能够提高燃烧过程的平均经济性能经济性和环保性。针对一些需要进行稳态工况调整的CFBB 燃烧过程,本文提出的算法更具有优势。

5 结论

考虑循环流化床锅炉燃烧过程在经济性能多变化条件下的目标优化问题,本文提出一种变经济性能Mo-MPC 控制算法。将引入的关于最优经济稳态点的正定辅助函数作为最高优先级目标,将床温设定值跟踪目标和燃烧经济目标作为次级优先目标,结合广义终端约束、字典序多目标优化和控制原理,设计循环流化床锅炉燃烧系统变经济性能多目标预测控制器。仿真结果表明,与传统字典序多目标优化算法相比,本文提出的算法既能够保证CFBB 燃烧过程在变化后的稳态工况下长期稳定运行,又能够提高燃烧过程中的经济性和环保性。