中国省域科技创新水平的空间溢出效应

高静 王燕 郭立宏

摘要：基于1999-2019年我国31个省份的面板数据，采用主成分分析的方法测度了各省市科技创新能力的综合评价指数，并在此基础之上通过全局Moran’s I指数分析了我国科技创新能力的空间溢出效应。实证结果发现：第一，我国科技创新能力在各省市上存在着较大的差异性，科技创新能力评价指数为正数的省份主要集中在北上广为中心的三个经济带;第二，全局Moran’s I指数在3个空间权重矩阵下均在显著为正，这说明我国的科技创新能力呈现出了正向的空间聚集性，并且在区位距离上的空间溢出效应更加明显。

关键词：科技创新;评价指数;空间效应

一、引言

党的十九大报告明确指出“创新是建设现代化经济体制的战略支撑，要加快创新性国家建设”。创新驱动发展战略是我国“新常态”下国家发展战略的核心组成部分，其有效实施能够推动经济发展方式转变以及新旧动能转换，实现经济提质增效升级。近年来，科技创新支撑经济社会发展的核心作用越来越受到重视，我国的科技创新水平也不断攀升，逐渐的缩短与发达国家的差距。近些年来，关于科技创新水平的相关问题引起了学者们的关注，进行了很多方面的研究。冯江茹（2019）使用随机前沿模型（SFA）测度了我国各省市的科技创新效率。王新红和李拴拴（2020）采用数据包络分析（DEA）测度科技创新效率。张洁（2019）运用Malmqist-DEA模型对我国各省市科技创新效率进行测度。王元亮（2020）采用DEA-Tobit两步法探究了科技创新效率以及影响因素。

从以上文献可以看出，现有研究对于我国科技创新水平进行了多种多样的研究，这其中包括指标体系的完善、科技创新效率的测度以及对科技创新影响因素的探究等。但是但鲜有学者从空间耦合的角度考虑科技创新水平。本文基于1998-2019年中国省际面板数据，构建了省域科技创新体系的评价指标体系，然后计算其全局Moran’s I指数，分析科技创新水平的空间效应。

二、科技创新能力评价指标

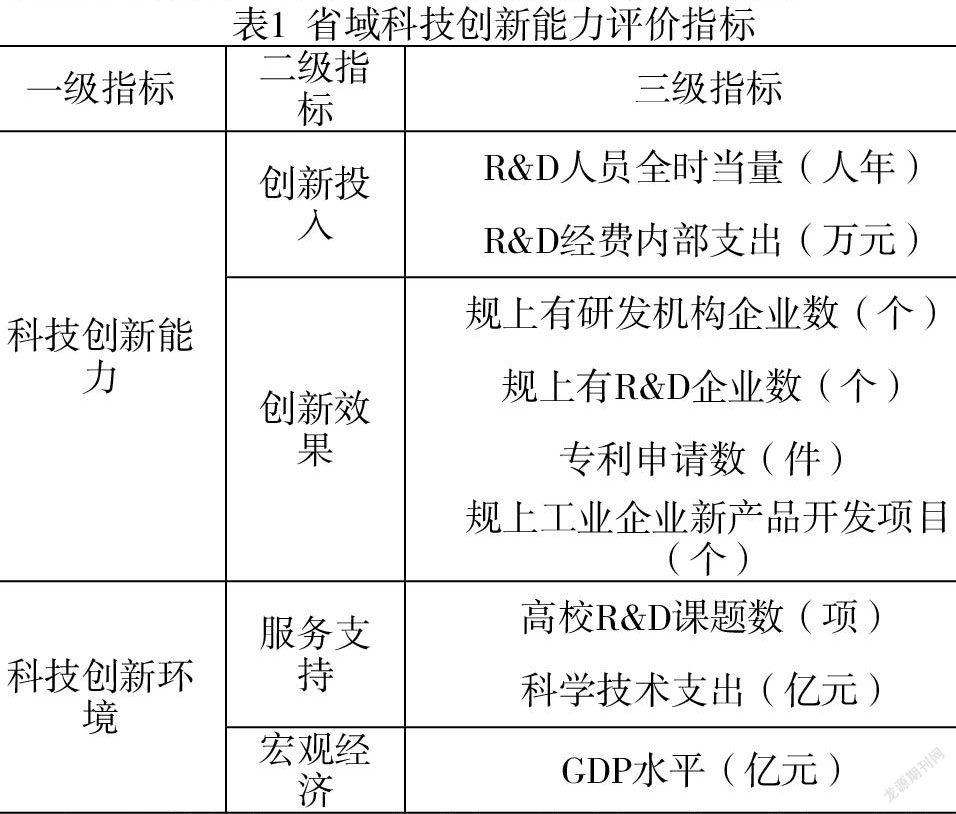
在弗里曼提出的国家创新体系中，企业是技术创新主体，政府是创新体系协调机构，为企业创新系统构造良好的政策环境并为之提供财政支撑;还有作为科学技术知识转移和扩散中介服务机构。以此为基础，再参考国内外已有的科技创新体系理论，本文构建了省域科技创新能力评价指标，如表1所示。

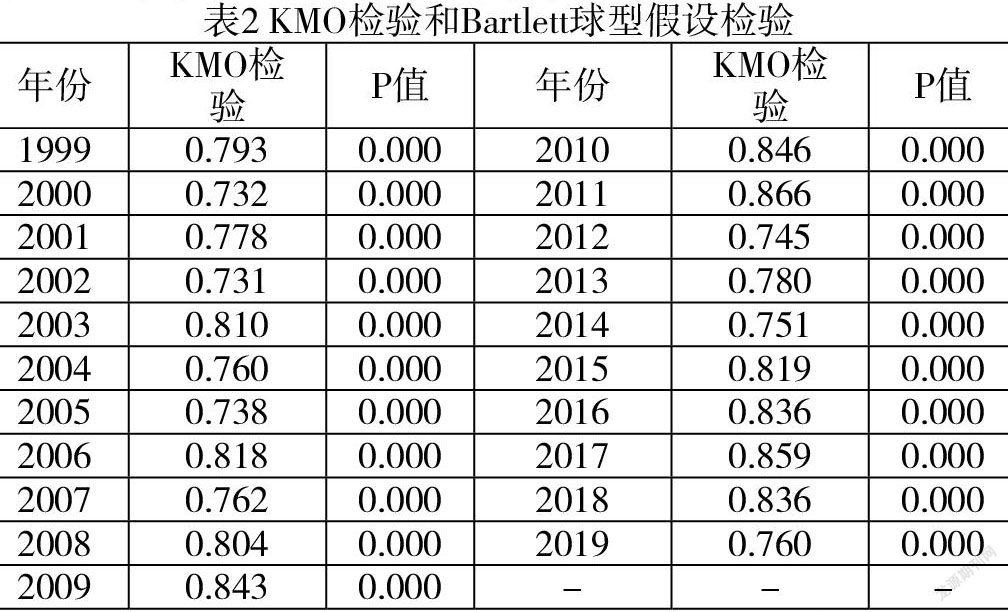
本文的数据来源于历年《中国统计年鉴》、《中国高技术产业统计年鉴》、《各省統计年鉴》、Wind数据库和国家统计局数据库等。本文对1998-2019年全国31个省市（不包含港澳台地区）的科技创新能力的8个指标数据进行整理后，首先使用对数据进行了KMO检验和Bartlett球型假设检验，结果见表2。

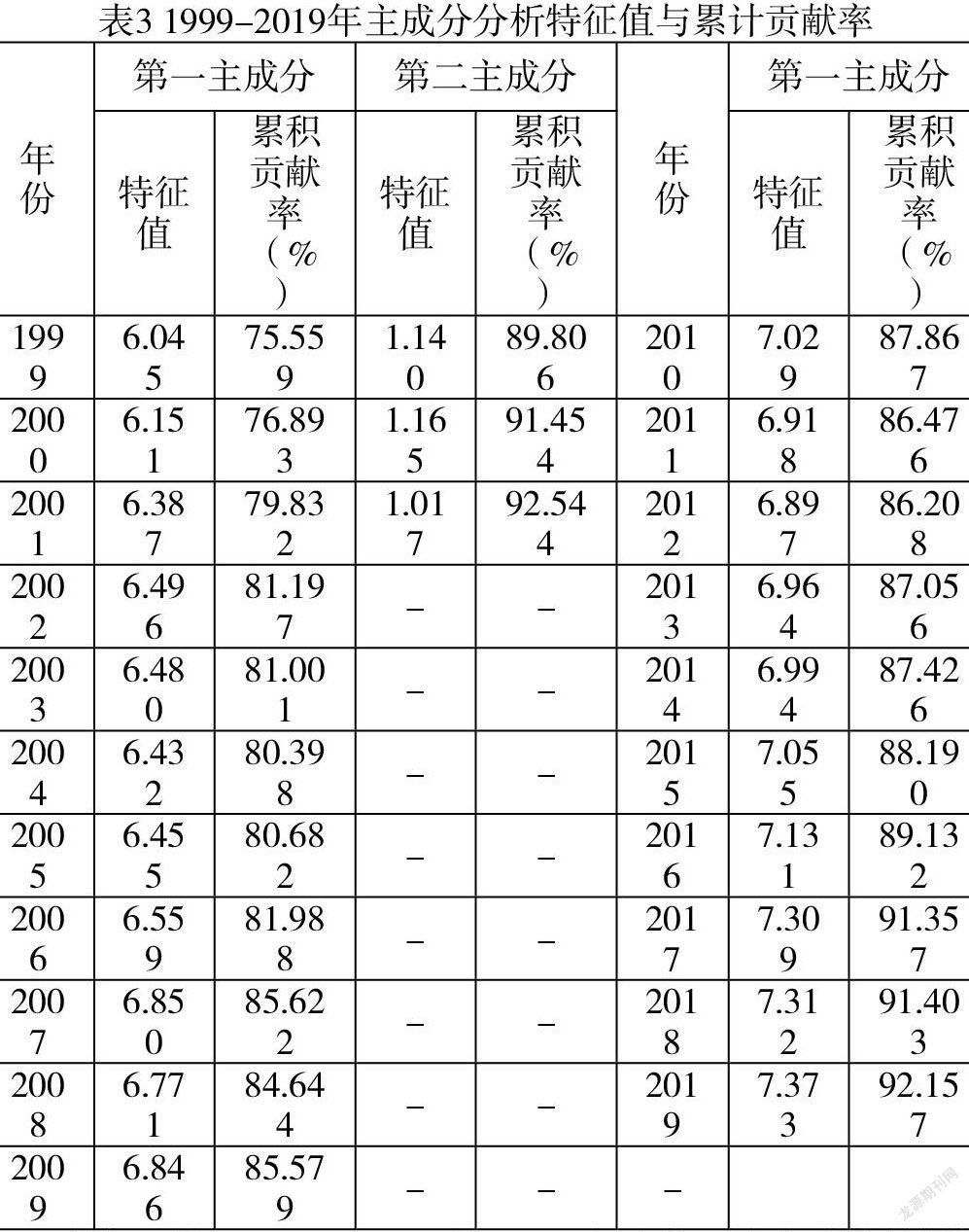
由表2的结果可以看出，1999-2019年的KMO数值均大于0.7，而Bartlett球形假设检验值在1%的水平下显著。进而通过主成分分析，可分别得到1999-2019年的特征值及贡献率，具体见表3.

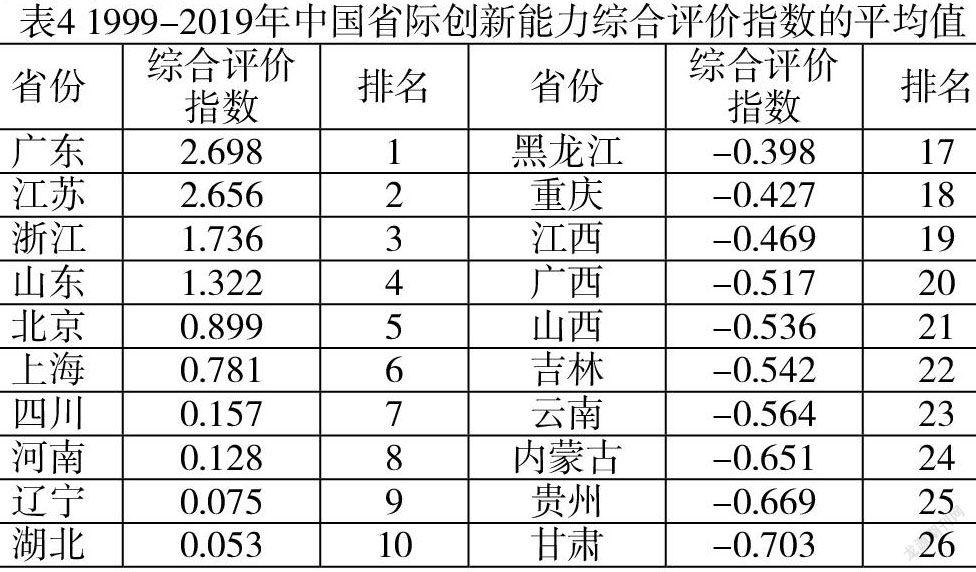
由表3可知，1999、2000和2001三年中前两个主成分的累计贡献率达到80%以上，2003-2019年第一个主成分的贡献率就都在80%以上，因此，样本数据中，1999-2001年数据有两个主成分，其余18年均只有一个主成分，可以计算得到相应的综合评价指数。为了讨论31个省市之间的差异，计算出各省市综合评价指数的均值，具体见表4

从表4得到的结果来看，创新能力综合评级指数最高的为广东，其综合评价指数为2.698，创新能力综合评级指数最低为西藏，其综合评价指数为-0.918，因此我国的各省市的科技创新能力呈现出极端分化的现象。科技创新能力综合评价指数为正数的省份为：广东、江苏、浙江、山东、北京、上海、四川、河南、辽宁及湖北，大部分为以北上广为中心的三个经济带上的省市，而科技创新能力综合评价指数为负数的多为经济相对落后的区域。

三、科技创新水平的空间聚集性分析

（一）理论机理

根据新经济增长理论，技术进步使得产业出现专业化趋势，因而造成空间聚集。从表1得知30个省市的区位熵有这很大的空间差异性，空间上的区域缺乏均质性。本文借鉴“地理学第一定律”来探讨高新技术产业集聚的空间效应。

本文运用全局Moran's I指数检验我国高新技术产业聚集的空间相关性。全局Moran's I统计量用于验证在整个研究区域内某一要素是否存在空间自相关，其计算公式为（Moran（1948））：

如果的值为正且显著，表示地区间存在正的空间自相关，如果的值为负且显著，表示地区间存在负的空间自相关，如果的值不显著，那么就不存在空间自相关。

（二）全局Moran’s I指数

在分析空间聚集性之前，都需要设定空间权重矩阵。基于已有文献，为此本文将选择如下3种权重矩阵：①地理距离W1（省会城市间的地表距离的倒数）;②边界因素W2（若有共同边界为1，否则0）;③区位因素（东、中、西、东北①）W3（若属于相同区位为1，否则0），并且将权重矩阵进行行标准化构成空间权重矩阵。

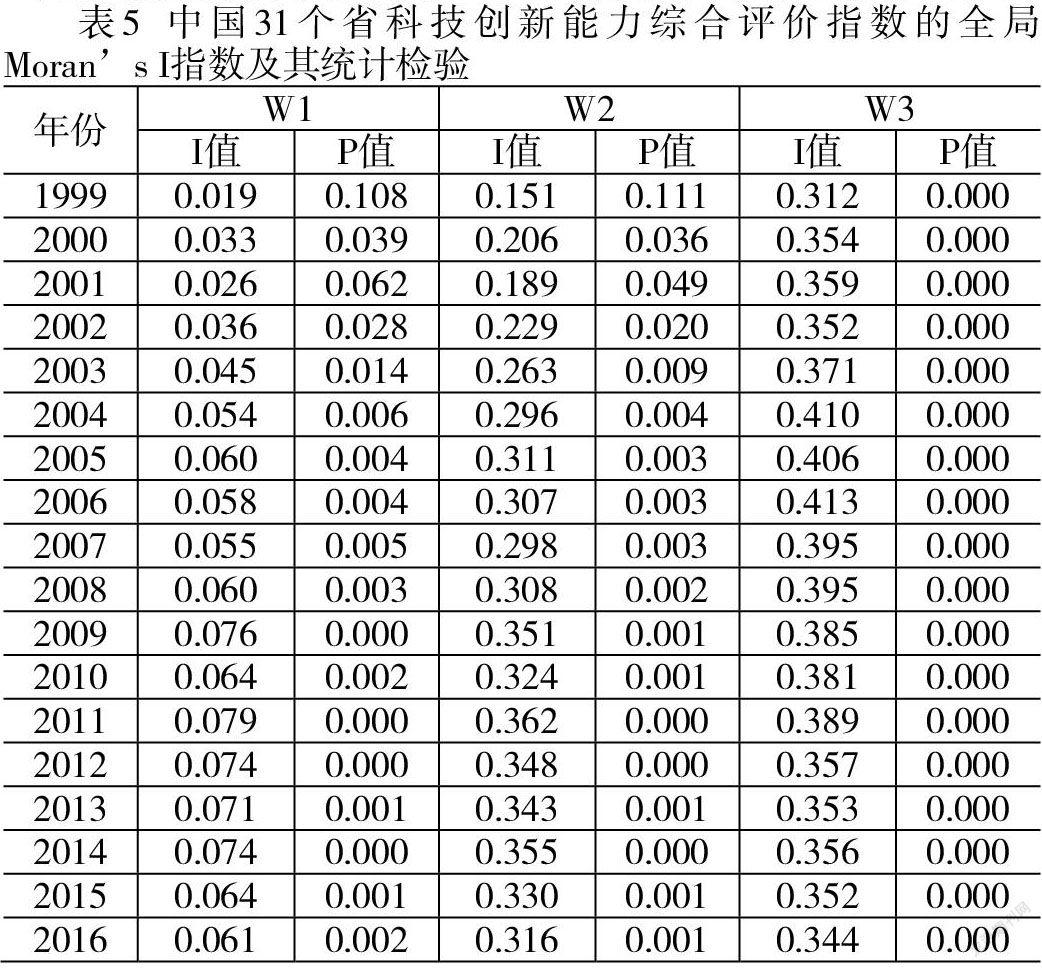
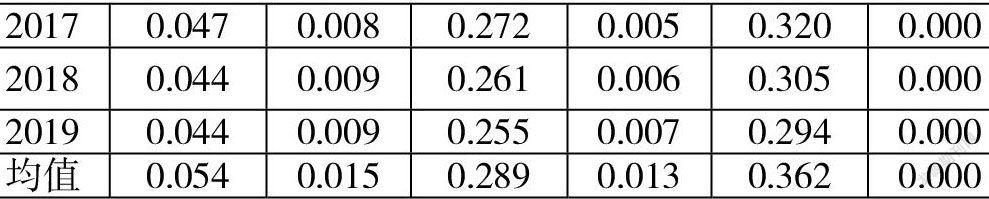
根据上文得到的各省市的科技创新能力综合评价指数，利用公式（2）得到了1999-2019年我国科技创新能力综合评价指数在3个空间加权矩阵下的全局Moran's I指数及其统计检验（见表5）。

从表5可以看出，在3个空间加权矩阵下，1999-2019年全局Moran’s I指数全部都是正数，除了1999年以外均在10%的水平下显著，这说明2000-2019年我国科技创新能力呈现出正向的空间将聚集性，即各省的科技创新能力会受到相邻省份的科技创新能力的影响。从空间权重矩阵来看，平均的全局Moran’s I指数在空间权重矩阵W1下最小，仅为0.054，并且显著性水平为1.5%;在空间权重矩阵W3下最大，为0.362，并且显著性水平接近0。W1与省会之间的地理距离相关，W2与省市之间是否相邻有关，而W3与是否在同一区位有关，从空间权重矩阵的构造可以看出，科技创新能力的综合评价指数的空间相关性在同一区位的影响和显著均最强。1999-2019年，3个空间权重矩阵下，我国31个省市科技创新能力综合评价指标的聚集水平呈现出了正向的空间聚集性，这说明各省市的科技创新能力空间评价指标受地理位置相邻省份的高新技术产业的聚集水平的影响。

四、结论

本文根据199-2019年31个省市科技创新相关数据，采用主成分分析的方法测度了各省市的科技创新能力综合评价指数，测度结果显示，我国科技创新能力存在着区域的不平衡、地区差异的现状。本文继续使用全局Moran’s I指数分析我国科技创新能力综合评价指数的空间相关性。主要结论是：第一，我国科技创新能力在各省市上存在着较大的差异性，科技创新能力评价指数为正数的省份主要集中在北上广为中心的三个经济带;第二，全局Moran’s I指数在3个空间权重矩阵下均在显著为正，这说明我国的科技创新能力呈现出了正向的空间聚集性，并且在区位距离上的空间溢出效应更加明显。

参考文献：

[1]Anselin L. Local Indicators of Spatial Association—LISA [J]. Geographical Analysis，1995，27（2）：93-115.

[2]Moran P. The interpretation on statistical maps [J]. Journal of the Royal Statistical Society，1948，10（2）：243-251.

[3]馮江茹.人力资本对区域创新效率影响的实证研究[J].技术经济.2020，38（12）：123-130.

[4]王元亮.河南城市科技创新效率评价及影响因素研究[J].区域经济评论，2020，（02）：75-83.

[5]王新红，李拴拴.基于数据包络分析的创新型企业技术创新效率测度研究[J].科技管理研究.2020，40（08）：59-64.

[6]张洁.我国各省市科技创新效率的DEA测评[J].价值工程，2019，38（30）：293-296.

注释：

①东部包括：北京、天津、河北、上海、江苏、浙江、福建、山东、广东和海南（10省市）;中部包括：山西、安徽、江西、河南、湖北和湖南（6省）;西部包括：内蒙古、广西、重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏和新疆（11省区市）;东北包括：辽宁、吉林和黑龙江（3省）.

基金项目：

河北省社会科学发展研究课题：河北省新兴产业集聚与科技创新耦合关系研究，20210301070;

河北省高等学校人文社会科学研究项目：海洋产业集聚与区域经济增长耦合关系研究，SQ2021030;

秦皇岛市社会科学发展研究课题：秦皇岛市县域科技创新对经济发展的测度，202LX099。

作者简介：

1.高静（1984—），女，汉族，河北人，讲师，数量经济学博士。主要研究方向：空间计量经济学理论及应用，宏观经济理论及应用。

2.王燕（1981—），女，汉族，河北人，副教授，管理科学与工程博士生。研究方向：产业集聚与绿色经济。

3.郭立宏（1978—），女，河南人，讲师，研究方向：网络营销。