软土地区基坑坑底隆起稳定破坏滑动半径研究

程雪松，甄 洁，郑 刚，王志勇，王 哲，宋许根

(1. 天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072； 2. 天津大学 建筑工程学院，天津 300072； 3. 中铁第四勘察设计院集团有限公司 道路交通设计研究院，湖北 武汉 430063)

0 引 言

随着城市建设的不断发展，地下空间已经得到广泛开发利用，基坑工程也朝着更深、更大的方向发展。在沿海软黏土深厚等土质条件较差的地区，基坑失稳事故时有发生[1-3]。基坑稳定性是基坑工程中的一个重要问题，现有的基坑隆起稳定性分析方法有很多局限性，在基坑失稳破坏的模式和滑动面等方面仍有较多问题需要解决。

目前，基坑隆起稳定性主要采用地基承载力模式和圆弧滑动模式2种极限平衡方法进行分析[4-5]。这些传统的基坑隆起稳定分析方法通常假定软土层强度均匀分布。在软土层较厚的情况下，破坏面覆盖整个坑底，导致破坏面过深，与实际不符。实际上，天然沉积的软黏土层强度通常表现出强烈的非均匀性，不排水抗剪强度一般随深度增加[6-7]。土体强度的不均匀性也会对坑底隆起失稳的破坏模式造成影响，会限制破坏面向深处发展。因此，在考虑软土地区基坑稳定性时，有必要考虑土体强度沿深度增长的特性。Khatri等[8]在研究无支撑垂直圆柱形黏土基坑稳定性时考虑了土体不排水抗剪强度随深度线性增加的特性。Chen等[9]在分析杭州地铁基坑坍塌案例时，也考虑了土体不排水抗剪强度随深度线性增长的特性。Goha[10]在考虑土体强度沿深度线性增长的条件下提出了轴对称黏土支护基坑坑底隆起安全系数的简化计算方法。郑刚等[11]合理考虑成层土及弧长和法向应力的影响后修正了圆弧滑动法，黄茂松等[12]提出了基于不排水抗剪强度的圆弧机构上限法。

已有工程案例及数值模拟结果表明，基坑发生坑底隆起破坏时经常出现围护结构的弯曲破坏[13]。地基承载力模式下的Terzaghi等[14]公式和Bjerrum等[15]公式，假设土体均质且墙体完全刚性，对于基坑深度和围护结构插入比均较大的情况适用性较差。王洪新[16]给出了考虑围护结构刚度和强度的Bjerrum破坏模式和相应的安全系数计算公式。黄茂松等[17]认为地基承载力模式适用于围护结构抗弯刚度较大且插入深度较浅的情况。宋二祥等[18]考虑下沉土体与稳定土体间竖直滑裂面的剪应力改进Terzaghi等[14]地基承载力方法，适用于挡土结构嵌固深度较小的情况。

在考虑围护结构弯曲破坏时，圆弧滑动法目前主要存在围护结构绕坑底和最下道撑为旋转2种破坏模式[19]。此方法可以考虑围护结构的抗弯强度对坑底隆起稳定的贡献，但其圆弧滑动面的选取仍值得深入研究。一般情况下，随着围护结构嵌固深度增大，圆弧滑动面增大，安全系数增大。黄茂松等[17]和宋二祥等[20]发现圆弧滑动法不适用于围护结构嵌固深度较小的情况。郑刚等[21]研究发现围护结构较短时，基坑坑底隆起滑动面不过围护结构底部，需进一步修正。需要指出的是，上海市《基坑工程技术规范》(DG/TJ 08-61—2010，简称沪规)的圆弧滑动法在围护结构插入比很小时求得安全系数过大，出现了随插入比增大安全系数减小的情况[20]。由此可见，传统圆弧滑动模式假设滑动面始终通过桩底是不合理的，其破坏滑动半径在嵌固深度较小时如何确定值得研究。Do等[22]提出了一种不用进行数值分析，将圆弧滑动法与土的数值破坏面相结合计算基坑隆起安全系数的简化方法。宋二祥等[20]考虑挡土结构嵌固深度提出了一种不同嵌固深度采用不同规范方法计算坑底隆起稳定性的验算方法。

本文采用不连续布局优化法(DLO法)对软黏土基坑坑底隆起破坏滑动面进行研究，探究了不同基坑开挖深度、土体强度和围护结构插入比条件下基坑隆起破坏滑动半径的变化规律，给出了基坑坑底隆起稳定分析时滑动半径选取的建议。

1 不连续布局优化法与模型验证

DLO法的基本原理为：外力做功和重力做功之和等于材料内部的能量耗散时，土体达到极限状态，沿着最小能量耗散的路径发生滑动。其本质上是一种数值化的极限分析上限法，借助Limit State GEO软件可实现基坑隆起滑动面的自动搜索和优化。与传统基坑抗隆起稳定分析方法相比，DLO法具有明显优势。

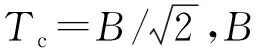
图1 DLO法与强度折减法得到的滑动面对比(T=0.75Tc)Fig.1 Comparison of Sliding Surfaces of DLO Method and Strength Reduction Method (T=0.75Tc)

图2 安全系数Fs随T/Tc变化规律Fig.2 Variation Laws of Safety Factor Fs with T/Tc

2 插入比对基坑隆起滑动半径的影响

2.1 模型建立

考虑土体不排水抗剪强度沿深度线性增长，其表达公式为

Su=Su0+λz

(1)

式中：Su为某个深度处土体的不排水抗剪强度；Su0为地表高度处的土体不排水抗剪强度，一般小于25 kPa[24-25]；λ为土体不排水抗剪强度沿深度方向的增长率，一般取值为0.6～3.0 kPa·m-1[24-25]；z为土体深度。

本文假定坑底以下软黏土足够深厚。考虑基坑的对称性，模型只取基坑右侧部分，如图3(a)所示。基坑坑底隆起的滑动面半径R定义为最下道支撑平面与滑动面底端所在平面的垂直距离，如图3(b)所示。

图3 基坑模型示意图Fig.3 Schematic Diagram of Excavation Model

2.2 滑动半径定性分析

对不同围护结构插入比D/H对基坑坑底隆起破坏滑动面的影响进行分析。基坑深度H=16 m，土体不排水抗剪强度Su=10+0.9z，考虑围护结构破坏，取其塑性弯矩Mp=2 000 kN·m·m-1。

不同围护结构插入比D/H下的滑动面如图4所示。可以看出，在围护结构插入比较小时，基坑隆起滑动面较小，且位于围护结构底端以下一定距离，这与郑刚等[21]所得结论一致。传统圆弧滑动法中滑动面始终通过围护结构底端的假设不合理。随着围护结构插入比增大，基坑隆起滑动面逐渐接近进而经过围护结构底端。随着围护结构插入比增大，滑动面恰好开始经过围护结构底端时的围护结构插入比定义为临界插入比(D/H)c。

图4 不同围护结构插入比下的滑动面Fig.4 Sliding Surface with Different Insertion Ratios of Retaining Structure

3 基于圆弧滑动法的基坑隆起滑动半径修正

3.1 滑动半径定量分析

本节在不考虑基坑宽度的影响下对基坑隆起滑动面的大小展开了定量研究和大量计算。通过DLO法计算得到不同开挖深度H、不同土体强度初值Su0、土体强度增长率λ和围护结构插入比D/H的基坑坑底隆起滑动半径，首先分析圆弧滑动面恰好通过围护结构底端时围护结构的临界插入比(D/H)c，继而研究围护结构插入比较小[D/H≤(D/H)c]时滑动半径R和围护结构插入比D/H的关系。

图5给出了不同开挖深度下土体强度增长率λ和围护结构临界插入比(D/H)c的关系，可采用幂函数y[(D/H)c]=a[x(λ)-b]c进行表达，其中a，b，c为系数。随着土体强度增长率λ增大，下层土体强度随深度更快速地增大，等效于下部硬土层越来越浅，滑动面恰好通过围护结构底端时的插入比逐渐减小。此外，土体强度增长率相同时，土体强度初值Su0越小，每米深的土体强度增长百分比越大，也可等效于下部硬土层较浅，故土体强度初值越小，滑动面通过围护结构底端所需的插入比越小。

图5 不同开挖深度下土体强度增长率λ与围护结构临界插入比(D/H)c的关系Fig.5 Relation Between Soil Strength Growth Rate λ and Critical Insertion Ratio (D/H)c of Retaining Structure with Different Excavation Depths

已知基坑开挖深度H，通过图5可以判断此基坑发生坑底隆起时滑动面和围护结构的关系。若围护结构插入比大于临界插入比，即D/H≥(D/H)c，滑动面通过围护结构底端，反之滑动半径需另行确定。

当围护结构插入比小于临界插入比时，考虑到表达简洁及滑动半径的定义，将滑动半径进行归一化处理，并表达为R/(D+h)。研究发现，归一化的滑动半径R/(D+h)和围护结构插入比D/H存在对数关系y[R/(D+h)]=a-bln[x(D/H)]，如图6所示。围护结构的插入比D/H越大，R/(D+h)的值越小，滑动面与围护结构底端的距离越近。当R/(D+h)=1时，滑动面恰好通过围护结构底端。其他开挖深度条件下滑动半径和围护结构也存在对数关系，通过大量的数值模拟和数据处理得到了一个表达式系数表，如表1所示。当围护结构插入比较小时，可通过表1修正传统圆弧滑动法的基坑隆起滑动半径，进而更准确地计算基坑抗隆起稳定性安全系数。

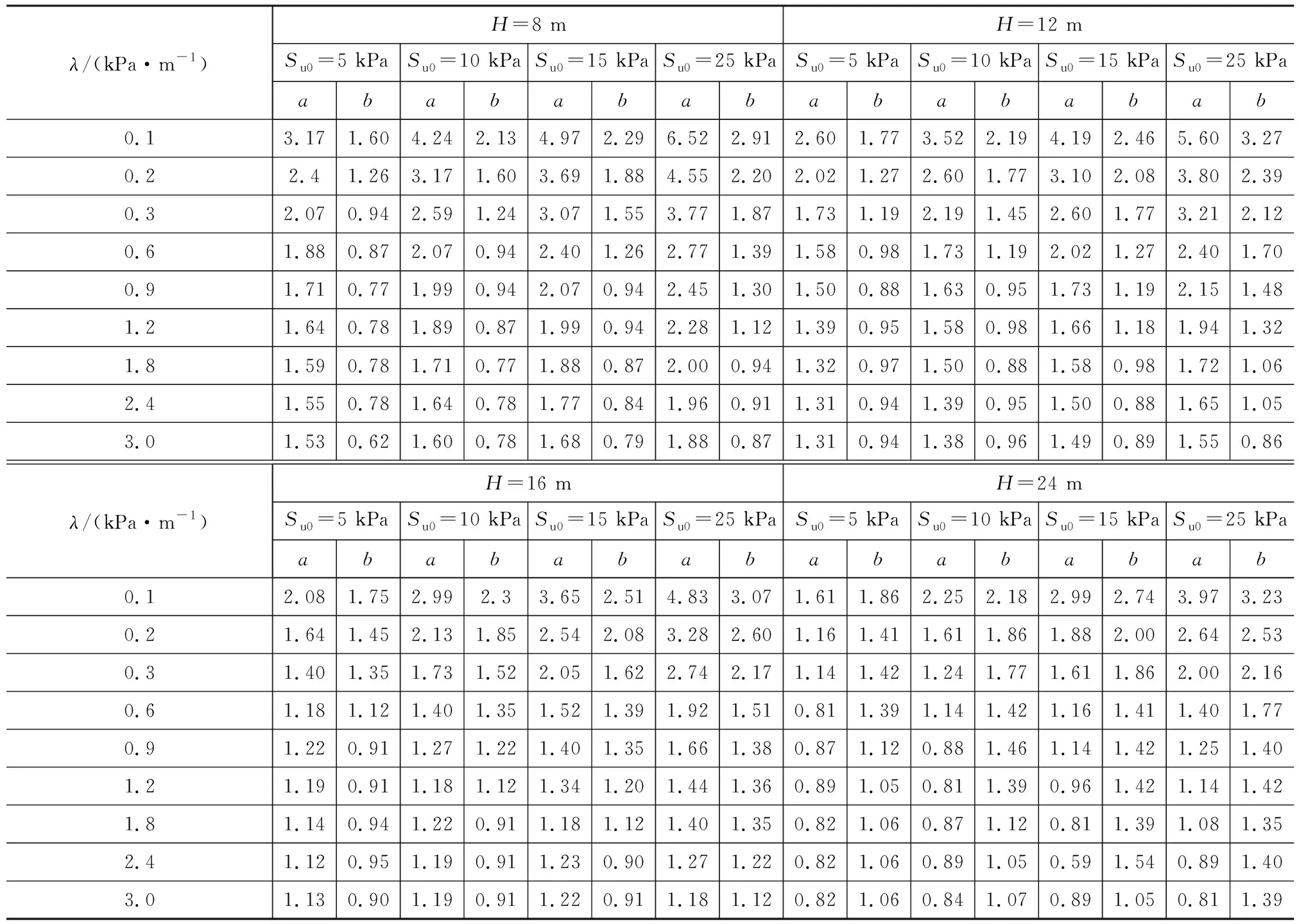
表1 归一化滑动半径与围护结构插入比的表达式系数Table 1 Expression Coefficients of Normalized Sliding Radius and Insertion Ratio of Retaining Structure

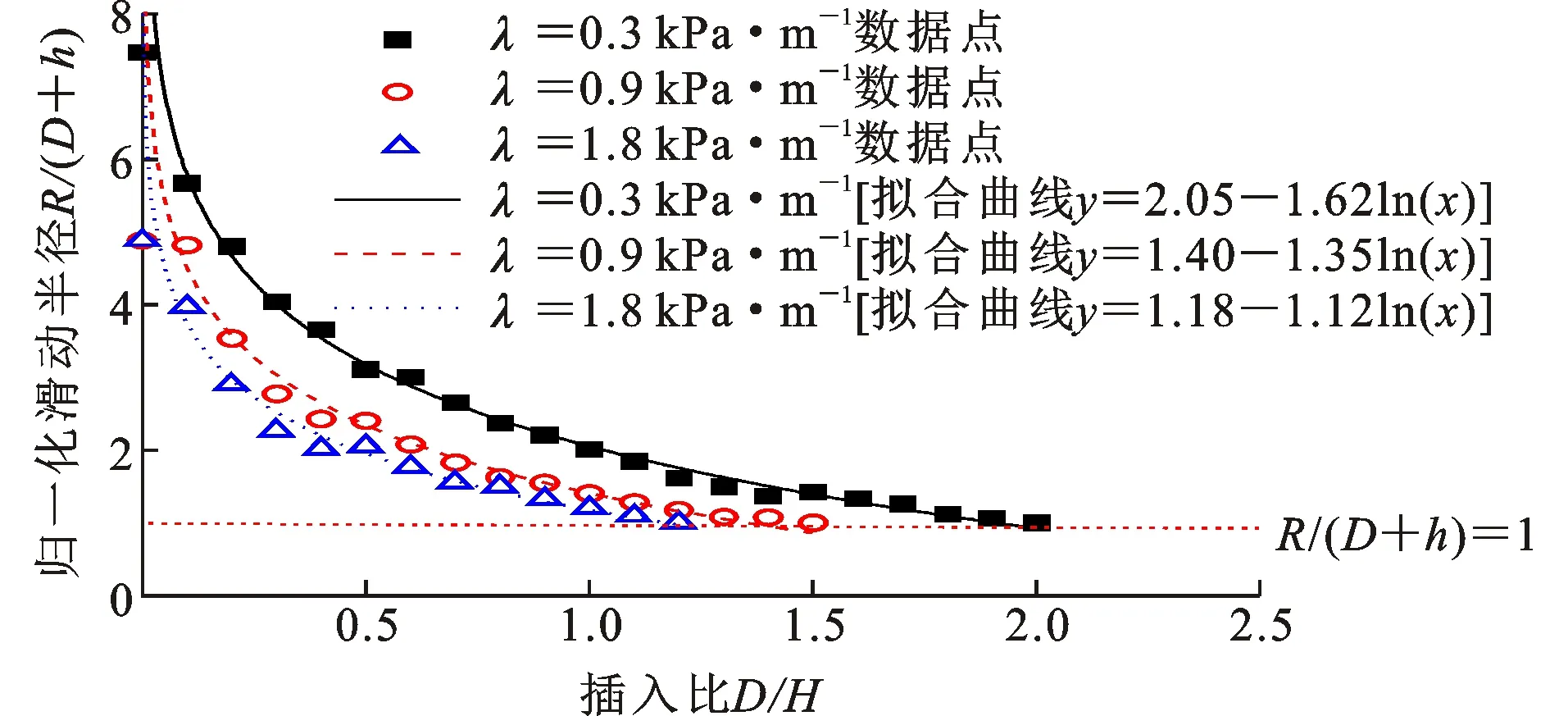
图6 归一化滑动半径R/(D+h)与围护结构插入比的关系(H=16 m,Su0=15 kPa)Fig.6 Relation Between Normalization Sliding Radius R/(D+h) and Insertion Ratio of Retaining Structure (H=16 m,Su0=15 kPa)

因此，本文建议利用圆弧滑动法计算软黏土基坑坑底抗隆起安全系数时，首先根据不同情况下土体强度增长率λ和围护结构临界插入比(D/H)c的幂函数关系判断滑动半径R是否需要修正，如D/H<(D/H)c，则利用归一化滑动半径R/(D+h)

和围护结构插入比D/H对数关系，结合表1确定修正后的R，进而将修正后的R代入传统圆弧滑动法计算坑底抗隆起安全系数。此方法在后文称为本文修正方法。

3.2 误差分析

本节对第3.1节拟合修正的滑动半径、修正后的安全系数合理性和可靠性进行分析，将本文修正方法得到的滑动半径和安全系数与DLO法数值模拟得到的结果进行对比。

图7为Su0=15 kPa、不同开挖深度和围护结构插入比下拟合滑动半径和DLO法计算的滑动半径误差直方图。图中共193个数据，82.90%的计算结果相对误差小于10%，98.96%的计算结果相对误差小于20%，极少数的相对误差略大于20%。可见，归一化的滑动半径对数表达式具有一定可靠性。图8为Su0=15 kPa、不同开挖深度和围护结构插入比下，基于修正后的滑动半径，利用圆弧滑动法计算得到的安全系数与DLO法安全系数的误差直方图。图8中相对误差结果均在10%以内，说明利用修正后的滑动半径计算的安全系数结果是相对可靠的。

图7 滑动半径拟合相对误差直方图Fig.7 Fitting Relative Error Histogram of Sliding Radius

图8 安全系数拟合相对误差直方图Fig.8 Fitting Relative Error Histogram of Safety Factor

图9为本文修正方法得到的安全系数与沪规法中圆弧滑动法计算结果的比较情况，正数表示修正滑动半径后安全系数得到了提高。图10为H=16 m，Su0=15 kPa时，DLO法计算得到的安全系数(DLO-Fs)、将DLO法计算的滑动半径代入沪规法计算得到的安全系数(DLO-R-Fs)、沪规法计算得到的安全系数(沪规法-Fs)、本文修正方法计算得到的安全系数(修正-R-Fs)的对比情况。

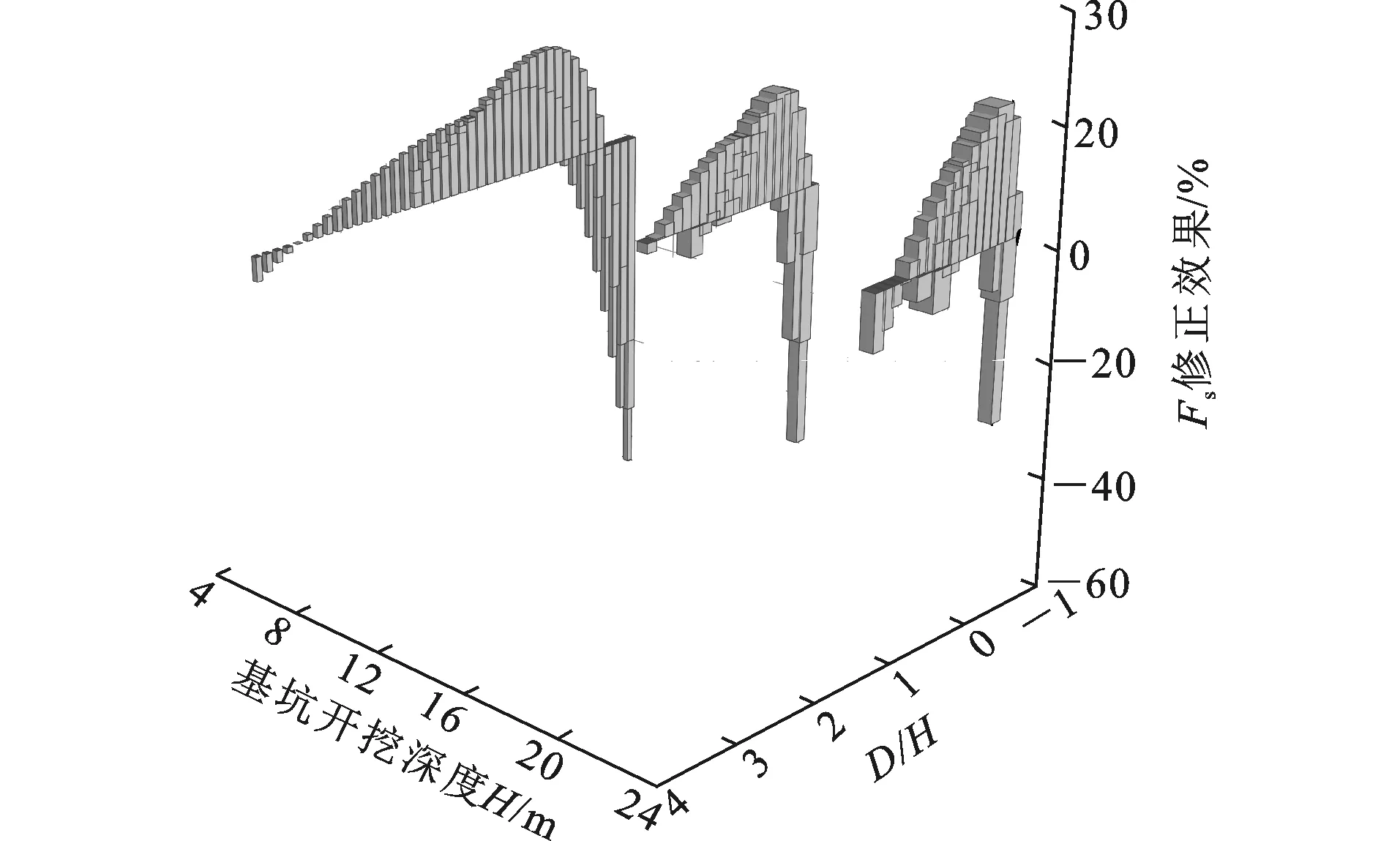
图9 安全系数修正效果直方图Fig.9 Histogram of Safety Factor Revised Effect

图10 安全系数比较(H=16 m,Su0=15 kPa)Fig.10 Comparison of Safety Factor (H=16 m,Su0=15 kPa)

由图9，10可见，在D/H适中(例如D/H在0.3～1.3之间)时，DLO-Fs和修正-R-Fs相比沪规法-Fs提高可达20%。当D/H<0.3时，修正滑动半径后的安全系数相对减小。这是由于沪规法考虑围护结构抗弯强度的抗滑贡献，在围护结构插入比很小时滑动面过围护结构底端，滑动面较小，土体提供的抗滑力矩和滑动力矩均很小，而抗弯强度很大，由此求得的安全系数过高，如图10所示。DLO法计算得到的安全系数DLO-Fs与本文修正方法得到的安全系数修正-R-Fs均随D/H增大而增大，且逐渐趋于平稳。可见，本文修正方法解决了沪规法在D/H较小时存在的安全系数计算不合理的问题。

4 结 语

(1)在围护结构插入比较小时，基坑隆起滑动面在围护结构底端以下一定距离，这与传统圆弧滑动法中假设滑动面过围护结构底端的计算模式不同。

(2)随着土体强度增长率λ增大，等效于下部硬土层越来越浅，滑动面恰好通过围护结构底端时的临界插入比逐渐减小。土体强度增长率相同时，土体强度初值Su0越小，相当于土体强度增长百分比越大，也可等效于下部硬土层越浅，由此临界插入比也越小。

(3)基于大量DLO法计算结果得到了围护结构临界插入比(D/H)c和土体强度的关系表达式y[(D/H)c]=a[x(λ)-b]c，可判断基坑隆起滑动面是否通过围护结构底端。

(4)在D/H<(D/H)c时，得到了不同基坑开挖深度、不同土体强度条件下归一化的滑动半径R/(D+h)与围护结构插入比D/H的对数表达式y[R/(D+h)]=a-bln[x(D/H)]及其系数表，可对传统圆弧滑动法的滑动半径进行修正，进一步确定基坑坑底抗隆起安全系数。此方法可以解决沪规法在围护结构插入比较小时安全系数变化不合理的问题。