基于HSS模型的上海地铁深基坑开挖变形分析
吴瑞拓,顾晓强,高广运,樊 烽,张 科
(1. 同济大学 地下建筑与工程系,上海 200092; 2. 同济大学 岩土及地下工程教育部重点实验室,上海 200092;3. 浙江祥生建设工程有限公司,浙江 诸暨 311800)
0 引 言
随着城市的不断发展,地下空间的利用率逐步提升,基坑工程得到了大规模应用,基坑工程的设计和理论也逐步完善。基坑的开挖容易引起周边环境变形,这些变形会对复杂的城市地下环境造成极大影响,引起周边结构的开裂甚至破坏,从而影响结构的正常使用[1],因此对基坑开挖引起的变形进行预测与控制至关重要。
大量工程监测数据表明,深基坑工程中的土体处于小应变状态[2],而土体刚度在小应变条件下具有高度非线性[3],因此在进行深基坑工程的变形分析时,有必要考虑土体在小应变条件下的刚度特性,采用能够考虑该特性的土体本构模型。

本文针对上海地铁某长条形深基坑的开挖过程进行了三维有限元分析,采用了能够考虑土体小应变刚度特性的HSS模型,分析了基坑围护结构侧移变形和坑外地表沉降变形的三维空间效应,并与现场变形实测结果进行了对比,以期为软土地区地铁车站深基坑工程的变形分析和控制提供参考。
1 地铁深基坑场地概况
该地铁深基坑场地位于上海轨道交通13号线祁连山南路站,场地资料来源于Tan等[18]。基坑宽约26 m,长约188 m,开挖深度为17.5~26.2 m,由东西2个竖井、换乘竖井以及由竖井隔开的2个标准段组成。图1为基坑的平面和测点布置图。基坑的开挖顺序为:开挖东竖井和标准段1,完成后开挖西竖井、换乘竖井和标准段2。土体开挖完成后立即施工支撑,基坑中部的换乘竖井将基坑分隔成了2个独立的区段。本文针对基坑的标准段1进行研究。标准段1的开挖宽度为20~22 m,长约60 m,最终开挖深度为17.5 m。场地土层分布见图2,其中,r为土体重度。该场地地下32 m范围内的土体为从软到硬的黏土和粉土,灵敏度为2.0~6.0,地下40.4 m处的土体为中密~密实的砂土,砂土层下部为较为坚硬的粉质黏土,长期地下水位位于地表下1 m。
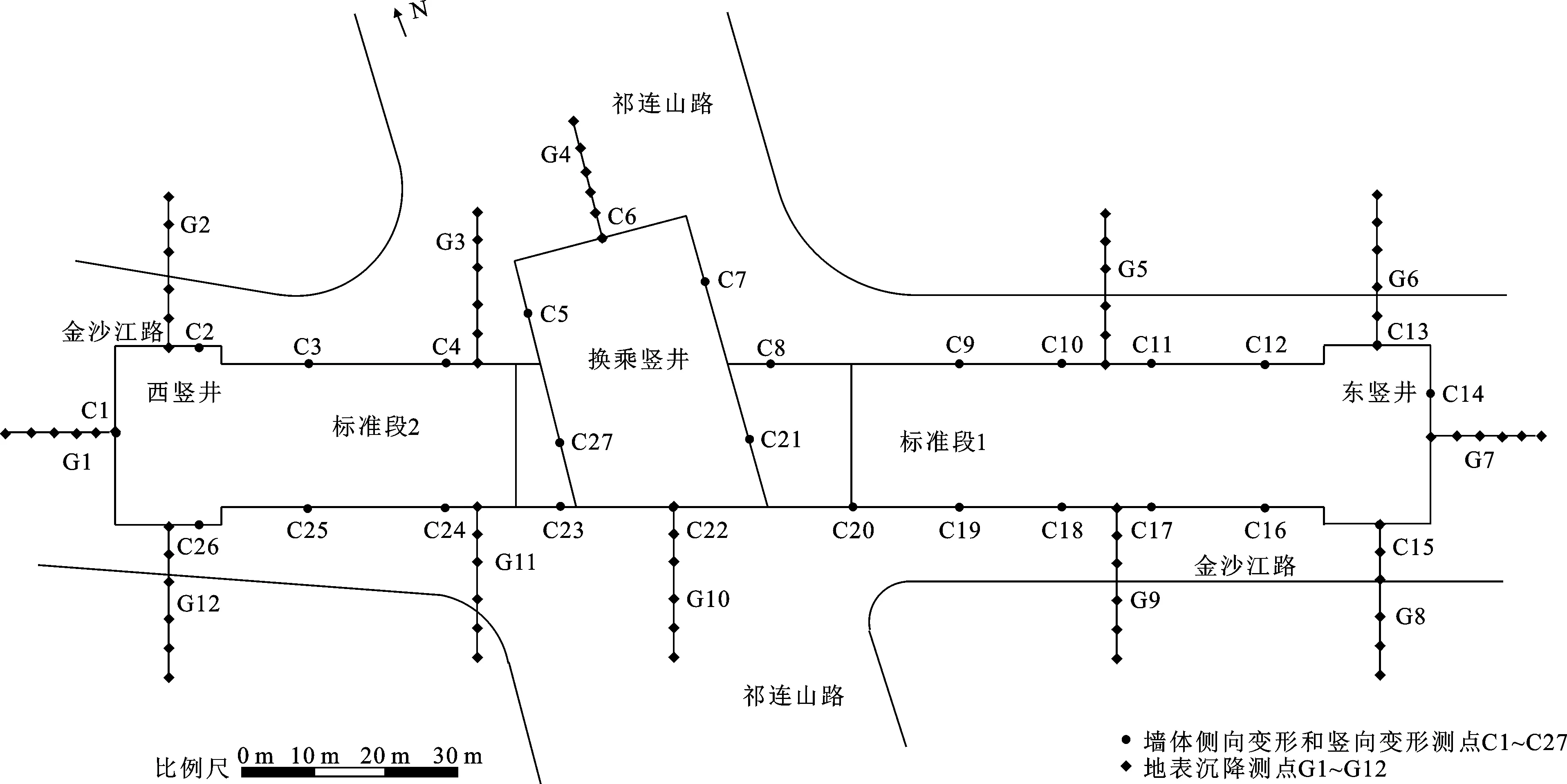
图1 基坑平面和测点布置Fig.1 Foundation Pit Plane and Layout of Measuring Points
2 基坑支护方案
基坑采用地下连续墙结合内支撑的方式进行支护。标准段1基坑采用5层内支撑,采用800 mm厚的地下连续墙进行围护,基坑的第1道内支撑为800 mm×900 mm的现浇钢筋混凝土支撑,其余内支撑均采用外径609 mm、壁厚16 mm的钢管支撑。钢筋混凝土支撑的水平中心间距为4~8 m,钢管支撑的水平中心间距为2~3 m。上海地区地下水位较高,在开挖过程中需要进行降水。为防止邻近基坑土体水位下降导致结构受损风险增大,对基坑进行了基坑底部注浆和基坑侧边的止水帷幕施工。在大多数情况下,基坑坑底注浆只是作为阻隔渗流的帷幕,并不会限制侧壁的运动。基坑支撑的剖面如图2所示。

图2 土层分布和基坑支撑剖面Fig.2 Profile of Excavation and Layout of Soil Layers
3 三维有限元模型分析
数值模拟分析计算中关键的问题在于土体本构模型的选取和模型参数的确定。选取的土体本构模型要既能够反映土的主要性质,又能够体现出基坑变形的主要特征。在确定本构模型基础上,根据试验和当地工程经验合理确定或选用模型参数,才能够达到较好的模拟效果。土的本构模型有很多种,但是被广泛应用于商业岩土软件的模型并不多。《基坑工程技术标准》(DG/TJ 08-61—2018)[19]中指出,硬化类的弹塑性模型能够较好地模拟墙体变形和墙后土体变形,适用于基坑开挖的数值模拟分析。HSS模型在HS模型的基础上,考虑了小应变范围内土体剪切模量随着应变增大而衰减的特点,更适用于敏感环境下的基坑工程变形分析。因此,本次模拟中的土体本构模型采用HSS模型。
3.1 有限元模型概况
采用PLAXIS 3D有限元分析软件建立祁连山南路站基坑开挖过程三维有限元数值模型并进行分析。数值模拟计算中,为了减小模型边界对计算结果的影响,模型高度建议为基坑开挖深度的2倍~4倍,模型一侧距坑边距离为基坑开挖深度的3倍~4倍。标准段1基坑开挖深度为17.5 m,因此有限元模型的高度设置为65 m,模型边界距基坑边界60 m,由此建立210 m×140 m×65 m的计算模型。数值模型由土体、围护结构和内支撑3个部分组成。模型中的土体均采用10节点的四面体实体单元模拟,地下连续墙采用6节点三角形板单元模拟,内支撑采用2节点点对点锚杆单元模拟。水平支撑的布置方式按照Tan等[18]给出的实际内支撑布置情况进行模拟。由于基坑底部的喷射注浆主要起防渗作用,对基坑变形影响较小,因此在模型中未考虑喷射注浆这一因素。模型底部同时对侧移和竖向位移进行约束,侧边仅约束侧移。整个有限元模型共划分79 743个单元、135 236个节点。
3.2 有限元模型参数取值方法
土体本构模型采用HSS模型,根据顾晓强等[17]提出的上海土体整套HSS模型参数方法并结合文献[18]中该项目的土层物理力学参数得到模型参数。为了更好地模拟基坑开挖过程,需要选择模型中土体的排水行为。在PLAXIS 3D有限元软件中,排水行为是指土体中的孔隙水可以自由流动,超孔隙水压力瞬间消散,这一类型适用于渗透性强的土,在模拟加载速度缓慢和长期效应时也可以采用。不排水行为则是指土体中的孔隙水无法排出,因此必须要考虑超孔隙水压力的影响。该类型适用于模拟渗透性弱的土或是模拟加载速度快及短期效应时。本文重点研究基坑开挖过程对周围环境的影响,主要考虑短期效应,因此模型中的黏土和粉土均采用不排水行为,对于渗透性强的砂土层则采用排水行为。各层土体的HSS模型参数见表1。
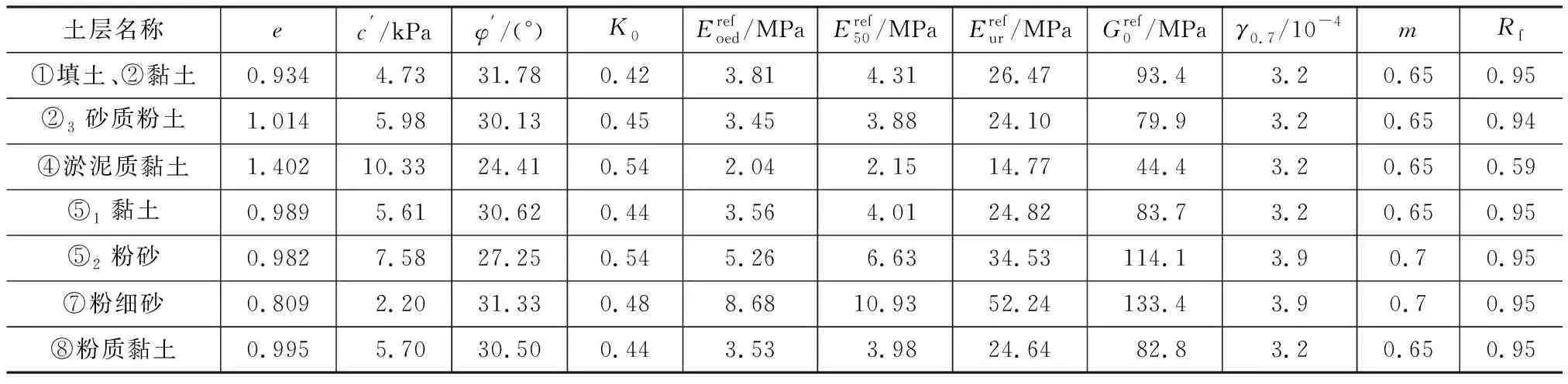
表1 各层土体HSS模型参数Table 1 Parameters of HSS Model of Soil Layers
基坑的围护结构和布置方式均按照实际工况进行模拟。地下连续墙和内支撑均采用弹性模型,地下连续墙和第1道混凝土内支撑的材料弹性模量为30 GPa,泊松比为0.2。钢管支撑的弹性模量为200 GPa。
3.3 有限元模型工况模拟
数值模拟中,地下连续墙施工、土体开挖和支撑的安装均按照项目的实际施工顺序设置。由于基坑底部注浆和基坑侧边设有止水帷幕,基坑的防渗漏措施到位,且黏土层的渗透性非常低,因此认为基坑的坑内疏干降水对坑外水位的影响很小。该基坑内外水的渗流同样可以忽略不计,所以基坑开挖过程中的降水模拟不需要进行稳态渗流分析,而是采用类组水头插值的方法来模拟基坑的降水开挖。在每一步的基坑开挖过程中,将基坑内的土体类组水头设置为开挖面下0.5 m,用来表示坑内水位降至开挖面以下0.5 m,基坑外的土体水头不改变,为天然地下水位。随着基坑开挖的进行,坑内水头逐渐降低。基坑四周5 m范围内设置20 kPa的竖向静荷载,用来模拟坑边的堆载。基坑具体开挖顺序如表2所示。
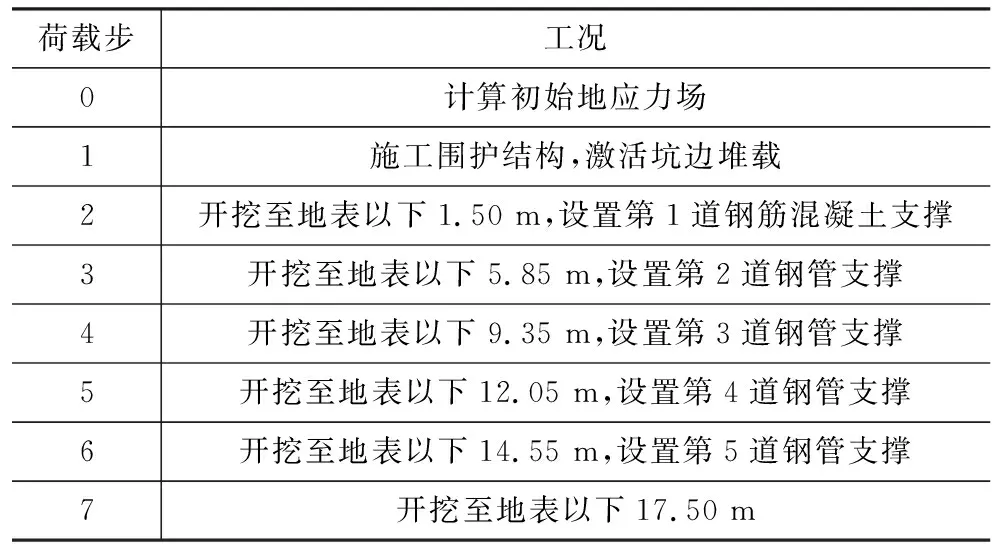
表2 标准段1基坑开挖顺序Table 2 Excavation Sequence of Standard Section 1
4 模型计算结果分析
4.1 围护结构侧移分析
图3给出了基坑标准段1开挖到不同位置时位于标准段1中部测点C17和端部测点C20测得的基坑围护墙侧移实测值和对应位置处的计算模拟值。从C17测点的实测值和模拟值可以看出,在开挖到第4层时,实测最大变形值为24.1 mm,而模拟最大变形值为16.4 mm,实测和模拟的围护墙最大变形均发生在第4层的开挖面处,约地下12 m处。在开挖到第5层时,实测最大变形值为33.8 mm,而模拟最大变形值为23.1 mm,实测和模拟的围护墙最大变形均在第5层的开挖面处,约地下15 m处。开挖到基坑底部时,实测最大变形值为46.5 mm,而模拟最大变形值为29.3 mm,最大变形发生在坑底附近,地下17.5 m处。模型的模拟值相比实测值偏小,约为实测值的70%,这可能是该测点位置附近的变形控制措施不到位导致。实测和模拟的变形模式接近,与Ou等[20]提出的深基坑变形模式类似,均为“内凸型”。随着基坑开挖深度的不断增大,基坑围护结构的侧移也逐渐增大。围护墙最大变形发生在当前基坑开挖面处。

图3 围护结构水平侧移Fig.3 Horizontal Displacements of Retaining Structures
从C20测点侧移的实测值和模拟值对比来看,不同开挖阶段的围护结构侧移最大值非常接近,但实测最大变形发生位置位于坑底上方5 m左右,而模拟的最大变形发生在坑底附近。
图4为标准段1其他测点的围护结构最大侧移实测值与模拟值的对比。所有测点实测最大侧移的平均值为31.6 mm,对应的模拟最大侧移值的平均值为26.9 mm,相差4.7 mm,差距较小。大部分测点的实测值同对应的模拟值非常接近,说明该三维有限元模型能够有效地模拟基坑围护结构的变形。同时基坑变形的空间效应也有所体现,位于基坑长边中部的测点C10,C11,C17,C18所测得的围护结构最大侧移明显大于基坑角部的测点值,其中C17测点的侧移值大于2倍的C20测点对应围护结构侧移值。三维有限元模型同样体现了基坑中部变形大于端部变形这一特点,表明长条形地铁深基坑有明显的空间效应,因此采用三维模型进行地铁深基坑模拟更加合理。

图4 不同测点处模拟和实测的最大侧移Fig.4 Maximum Horizontal Deformations of Different Points in Simulation and Measurement
4.2 坑外地表沉降分析
图5为基坑开挖到坑底时,基坑中部的坑外地表沉降模拟值和对应位置测点G5的实测值对比。G5测点的实测值有所缺失,但从获得的3个孔位的数据对比来看,实测点落在了模拟坑外地表沉降曲线附近,模型较好地模拟了坑外地表沉降变形,说明采用该模型能够较好地预测基坑开挖过程中坑外的地表沉降。实测坑外地表沉降的最大值为32.1 mm,发生在距坑边5 m范围内,为开挖深度的0.29倍。模拟的坑外地表沉降最大值为23.4 mm,位置在距坑边3 m处,为基坑开挖深度的0.17倍。基坑的坑外地表沉降曲线形状接近Hsieh等[21]给出的沉降曲线模型。沉降测点G5位于C10与C11测点之间,C10与C11测点的实测平均最大侧移值为34.0 mm,G5测点处的模拟最大侧移值为29.3 mm。研究结果表明:模拟的坑外地表沉降最大值δvm与模拟的围护结构水平最大侧移δhm之比为0.80,最大地表沉降实测值δvm与围护结构最大侧移实测值δhm之比为0.94。这一结果与王卫东等[22]提出的上海地区地表最大沉降δvm介于0.4δhm~2.0δhm的范围吻合,其平均值为0.81δhm。
从围护结构水平侧移和坑外地表沉降结果可以看出,三维有限元模型的计算结果同实测结果较为吻合,并且符合相关研究提出的基坑变形曲线模型,说明采用HSS模型及相应的模型参数能够有效地预测基坑开挖的变形,三维有限元模型能够很好地体现出基坑开挖变形的空间效应。
5 结 语
(1)数值模拟分析结果表明,采用HSS模型和合理的参数取值方法能够有效地模拟上海地区地铁深基坑的变形,对工程施工有较好的指导作用。
(2)基坑的端部与中部变形差距较大,采用二维平面应变模型无法体现这一现象,利用三维有限元模型进行基坑开挖的数值模拟更为合理。
(3)长窄型地铁基坑的坑长边中部位置的围护结构侧移大于基坑角部位置,呈现明显的空间效应,建议利用三维有限元模型进行基坑开挖的数值模拟。在工程设计中,应重视基坑长边中部位置,做好针对性措施。

