基于正则化模型的RLS算法改进
孙 帅,刘子龙,万 伟
(上海理工大学 光电信息与计算机工程学院,上海 200082)
在利用生物雷达进行生命体征监测的过程中,外界环境干扰及待检测目标自身的一些活动会影响监测结果的准确性。由于目前无法提前了解外界环境中各种复杂干扰信号的特性以及随时间推移而产生的变化规律,因此在复杂的外界情况下,仅通过传统固定系数的过滤系统已无法获得理想的过滤效果[1]。
依据自适应原理可以对滤波参数进行调试,使自适应系统能够完成对实变信号的滤除[2]。自适应算法在收敛速度、稳态失调、算法复杂度等方面各有不同。自适应算法的优点是在处理实变信号时仍可以保持较为理想的输出信号,且能够有效减少因系统本身计算产生的误差;其不足之处在于稳定性以及收敛速度不够理想。针对以上问题,本文提出了一种改进算法:基于正则化模型增加改进函数使遗忘因子增加可变性,并改进自相关矩阵逆矩阵方程[3],从而提高算法收敛速度、跟踪能力以及稳定性。
1 RLS算法
20世纪60年代,为了解决旁瓣干扰的问题,研究人员提出了最初的最小均方算法(Least Mean Square,LMS)模型[4]。随着研究的不断深入,在LMS算法模型的基础上又演变出递推最小二乘算法(Recursive Least Square,RLS)[5]。
RLS算法的改进之处在于可在待测数据长度不断变化的情况下求均方误差,而且根据时间先后分别乘了加权因子[6]。因此,可得该算法的均方误差为
(1)
式中,β(k,n)是加权因子,满足0<β(k,n)<1。经过n次迭代,以前的数据可以忽略。当环境中杂波信号不稳定时,待测数据可能仍会遵从之前的特性。
通常情况下,遗忘因子为指数加权因子的形式,即
β(k,n)=αk-n,n=1,2,…,k
(2)
式中,α是一个接近1但小于1的数。均方误差的表达式为
(3)
当ξ(k)为最小时,有以下关系
R(k)×w(k)=p(k)
(4)
式中,R(k)与p(k)定义如下式所示。
(5)
(6)
基于上述理论分析,能够得出RLS算法通过对获得信号自相关矩阵的逆矩阵进行特殊的处理,可以有效解决LMS算法缺点带来的影响。与LMS算法相比,RLS算法在收敛速度和跟踪能力上都有所提升[7]。但是,通常情况下RLS算法的遗忘因子是不变的,因此系统无法在跟踪速度和稳定误差两方面同时达到最优。而且当参数估值约等于实际值时,卡尔曼增益向量无限趋于0,此时会导致系统丧失跟踪能力[8]。
2 基于正则化模型的RLS算法改进
针对上述问题,本文提出了一种基于正则化模型的改进算法。该算法基于正则化模型增加改进函数使遗忘因子增加可变性,并且改进自相关矩阵逆矩阵方程[9],最终在收敛速度、跟踪能力、稳定性等方面得到了较好的提升。
2.1 正则化模型
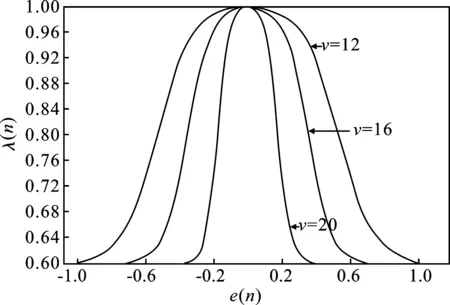
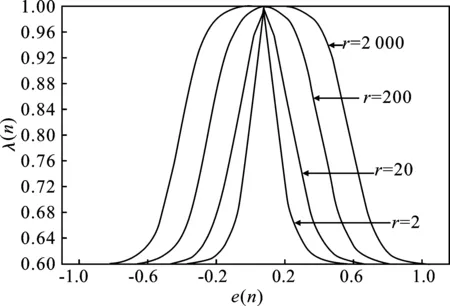
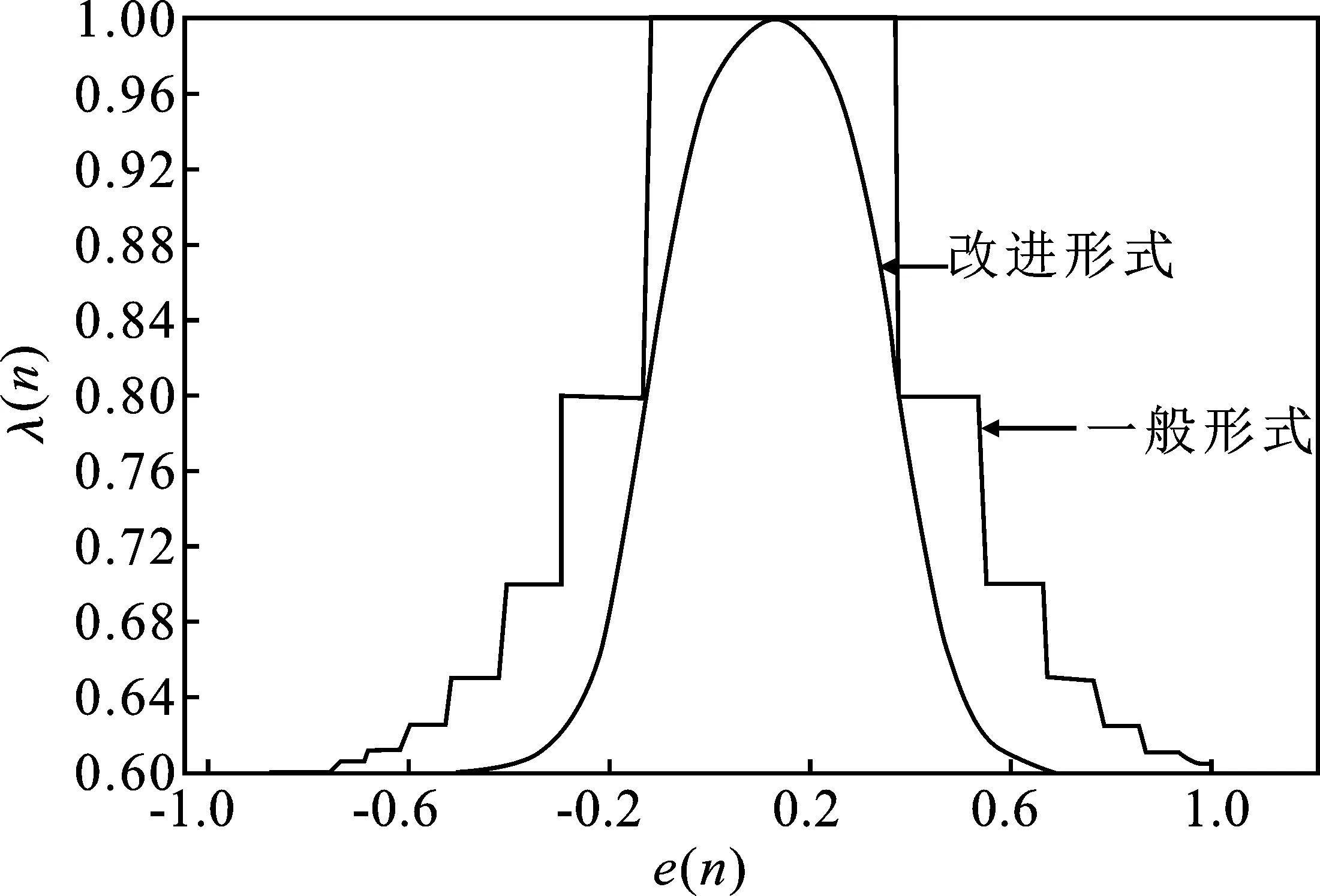
针对此模型,用x(n)表示信号,其中1 (7) TV(x)还可表示为TV(x)=‖Dx‖,其中D为N×(N+1)的矩阵。 (8) 不含杂波的原始信号表示为x(n),含有杂波的信号用y(n),即 y(n)=x(n)+ε(n) (9) 式中,ε(n)为高斯噪声。 与其他降噪方式不同,依据总变分正则化模型的方式,可以通过增加相关限制条件将杂波信号降噪为原始信号,且能够保证降噪效果存在且唯一,可以有效减少杂波的干扰[10]。根据已有的模型可以将杂波消除转化成求解目标函数最小化的方式,其中目标函数定义为 (10) 式中,λ为正则化参数。可通过改变λ的大小来控制权重。 带改进因子的RLS算法可以表示为 J(n)=∑λn-ie2(i) (11) 式中,i=1,2,…,n;λ为改进因子,并且满足0<λ<1。 算法如下 e(n)=d(n)-xT(n)w(n-1) (12) (13) w(n)=w(n-1)+k(n)e(n) (14) (15) λ(n)=λmin+(1-λmin)2L(n) (16) L(n)=-round[μe2(n)] (17) 式中,x(n)表示n时刻的输入信号矢量;w(n)表示n时刻的权矢量;d(n)为n时刻的期望输出信号;e(n)为先验误差;k(n)为卡尔曼增益矢量;p(n)为n时刻的输入信号自相关矩阵的逆矩阵;λ(n)表示n时刻的遗忘因子;round表示最接近μe2(n)的整数。 当误差变小时,λ(n)就接近1,使参数的误差减小;反之当误差变大时,λ(n)就变小至最小值λmin,这样可以加强系统跟踪能力[11]。 由以上的算法基础能够推演出新的降噪算法,详细过程如下:含有杂波的信号记为y(n),原始不含杂波的信号记为x(n)。根据以上算法可知,可以将求取最初的原始信号转化为求目标函数最小值问题[12]。 (18) 式(18)中的目标函数J(x)可转化为 (19) (20) 若要求得目标函数式(20)最小向量x,可以通过构造相应的辅助函数 (21) 求解式(21)的最小值问题转换为 (22) 由于F(x,z)在x方向为凸的,在z方向是凹的,根据极值的特性,能够调换最值的顺序 (23) 对F(x,z)关于x求导可得 (24) 将上式代入式(22)中得 (25) 可以转化为等价的求解最小化问题。 (26) 式(25)是一个具有不等式约束的条件极值,通过常规的方式不便于求解。本文通过最小化方法进行求解,令 (27) G(z,z(i))=F(z)+(z-z(i))T(αI-DDT)(z-z(i)) (28) 式中,z(0)为初始向量,取参数α不小于DDT最大特征值[13]。则(z-z(i))T(αi-DDT)(z-z(i))是一正定或半正定二次型,因此有: (1)对任意的z有G(z,z(i))>F(z); (2)在z(i)处,G(z(i),z(i))=F(z(i)),求G(z,z(i))的最小值,记为z(i+1)。 为了验证RLS改进算法杂波滤除的效果,本文将对采集到的呼吸信号进行实验验证,采用高斯噪声进行仿真验证。图1为采集到的正常人体呼吸信号波形图,图2是高斯噪声,图3为人体呼吸信号和高斯噪声的叠加信号。 图1 呼吸信号图Figure 1. Respiration signal diagram 图2 噪声波形图Figure 2. Noise waveforms 图3 呼吸信号与高斯噪声混迭信号Figure 3. Respiratory signal and Gaussian noise mixed signal 图4 基于LMS算法的误差曲线Figure 4. Error curve based on LMS algorithm 图5 基于RLS算法的误差曲线Figure 5. Error curve based on RLS algorithm 通过对比图4和图5能够明显看出,基于RLS算法的自适应过滤系统在信号迭代过程中形成的误差小于基于LMS算法所形成的误差。根据以上实验的验证可知,基于RLS算法的自适应过滤系统在信号滤除的过程中收敛速度较快,而且精度高、稳定性强,能够有效地对杂波信号进行滤除,对于不稳定的信号仍能达到较为理想的效果[14]。而基于LMS算法的自适应过滤系统在信号滤除的过程中收敛速度则较为缓慢,计算精度不够且稳定性差。 本文提出改进函数的方法:引入参数r改善函数形状,s控制参数范围。常数t和s控制函数的取值范围,常数v与常数r控制改进函数收敛速度快慢。 图6为常数v分别取12、16、20时,λ(n)与e(n)的关系曲线图。图7为常数r分别取2、20、200和2 000时,λ(n)与e(n)的关系曲线图。λ(n)表示n时刻的遗忘因子,e(n)为先验误差。 图6 v变化时λ(n)与e(n)的关系曲线图Figure 6. The relationship between λ(n) and e(n) when v changes 综合两图可知,常数v对收敛速度产生了关键影响[12],而r则对改进函数产生主要影响,对收敛速度也有相应的影响。若要获得理想的收敛速度和跟踪能力,需要增大v值,减小r值;若要获得理想的稳态误差,需减小v值,增大r值[15]。 图7 r变化时λ(n)与e(n)的关系曲线图Figure 7. The relationship between λ(n) and e(n) when r changes 常数t和s可以控制改进函数的取值范围。当|e(n)|趋近于较大值,例如1时,λ(n)趋近于s;当|e(n)|为0时,λ(n)=s+t,即s<λ(n) 图8 遗传因子改进前后对比图Figure 8. Comparison chart before and after genetic factor improvement 图8中,改进的遗忘因子参数为v=20,t=0.1,s=0.6,r=200;基本改进遗忘因子参数选取μ=12;遗忘因子最小取值均为λmin=0.6。在初始阶段或者系统发生突变的情况下,λ(n)迅速下降,从而获得理想的收敛速度和跟踪速度。在系统进入平稳状态后,λ(n)保持不变,来调整稳态误差较小的情况[16-17]。 LMS算法在稳定的环境中有着较好的收敛效果,算法的复杂度较低,能够在有限精度的情况下实现理想的杂波滤除效果。在求均方误差时,RLS算法待测数据的长度是实时变化的。本文提出的改进算法通过增加改进函数使改进因子增加可变性,并改进了自相关矩阵逆矩阵方程,有效地改善了算法的收敛速度、跟踪能力和稳定性。本文实验采用的是理想状况下的输入信号,然而在实际应用中,外界环境的干扰复杂多变。在输入信号含有多种干扰的情况下,本文所提算法在收敛速度、跟踪能力、稳定性方面的效果会有所降低。此外,本文所提算法的实时动态过滤效果欠佳。因此,在今后的研究中,将重点改进算法的动态过滤效果,以使该算法在实际工程中得到更加广泛的应用。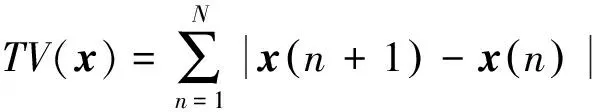
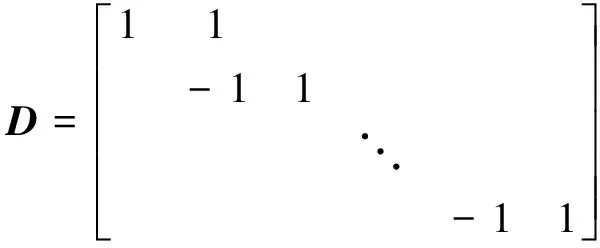
2.2 算法改进
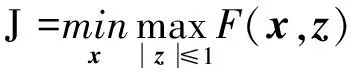
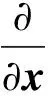
3 实验与仿真
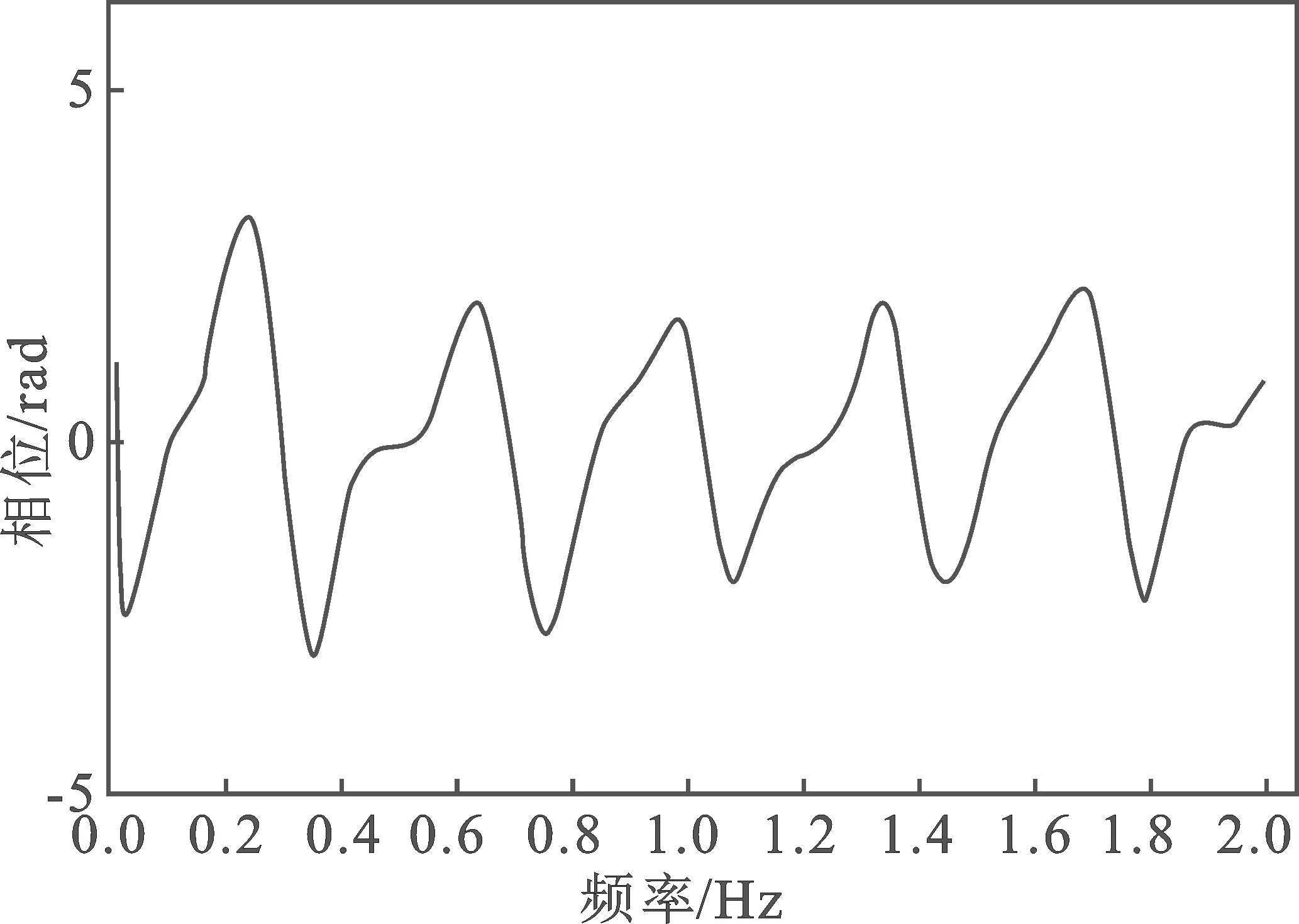
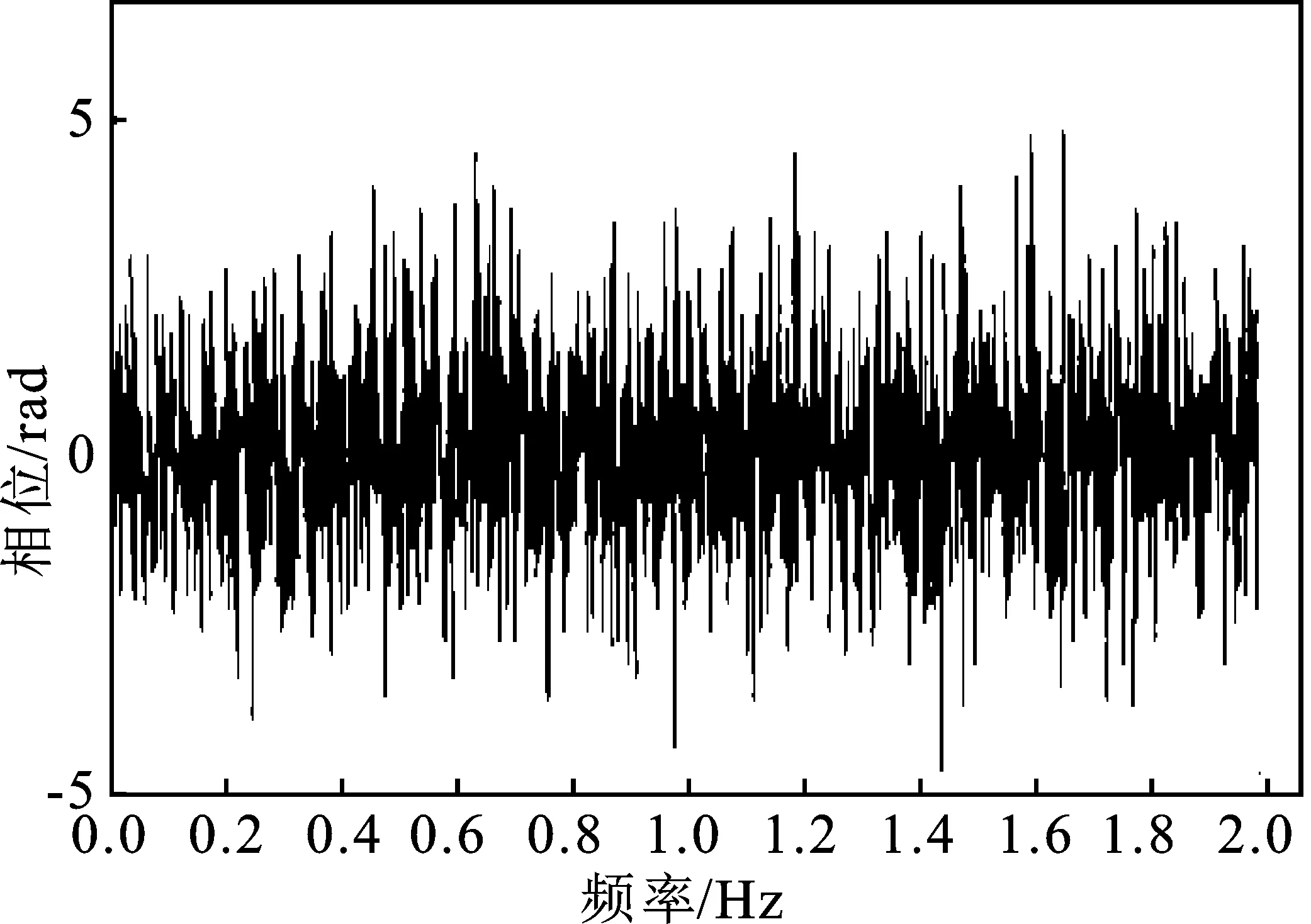
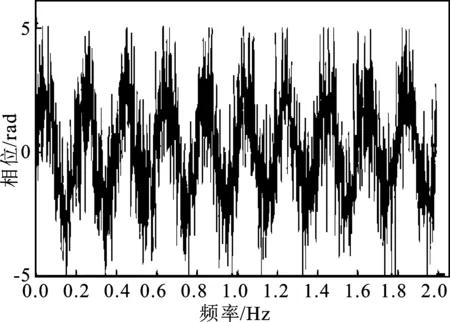
3.1 LMS与RLS对比实验

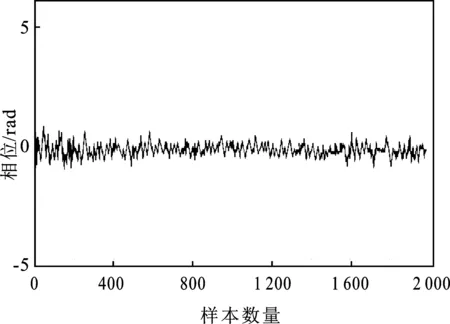
3.2 RLS算法改进前后对比实验
4 结束语

