容错控制下电磁轴承磁极故障磁场解析
王佳良,蒋科坚,朱芳甫
(浙江理工大学 信息学院,浙江 杭州 310018)
主动电磁轴承(Active Magnetic Bearing,AMB)无需润滑,无摩擦损耗且具有高转速,满足高速转子的性能要求,可被用于轴承的高端应用中。在容错控制下,当电磁轴承磁极出现故障时,提高转子的悬浮性能是目前电磁轴承的主要研究方向之一。
传统的8极径向差动控制电磁轴承大多使用异极型支承结构,即沿着圆周以NNSS拓扑结构排列。其也有一部分使用同极型支承结构,沿圆周只有N或S极,每一个磁极对沿轴向分布。这两种支承结构都采用相邻的两个磁极单独形成一个磁极对的拓扑结构[1-4]。文献[5]提出了广义偏流线性化理论,可使任意拓扑结构磁轴承的电磁力转化成电流的线性函数,为容错控制提供了理论基础。国内外学者对传感器[6-8]、控制器[9-10]、执行器[11-17]等容错控制方面进行了深入研究。文献[6]对磁悬浮轴承的位移传感器故障类型进行了分类, 提出了位移传感器的冗余布置方法。文献[7]提出了一种基于自适应滤波的传感器故障诊断方法。文献[8]提出通过观察输出信号的幅值判断传感器短路及断路故障方法。文献[9]针对控制器不同的故障类型,研究了相应的故障诊断与处理方法。文献[10]提出一种基于ARM+DSP架构的双核处理器来满足多自由度磁悬浮的故障诊断与实时控制。文献[11]采用拉格朗日乘数法计算出永磁体电磁轴承的电流分配矩阵。文献[12]根据强耦合结构电磁轴承提出了坐标变换法的执行器容错控制方法,减少了电流分配矩阵的数量。文献[13] 利用牛顿-拉普逊的数值方法计算出5种故障情况下的电流分配矩阵。文献[14]提出一种反馈线性化与保性能控制相结合的容错控制策略。文献[15]提出了力平衡法电流重构方法,并在弱耦合结构磁力轴承上对此方法进行验证。文献[16]和文献[17]提出了具有紧耦合冗余支撑结构的径向电磁轴承的容错控制策略。
现阶段执行器容错控制的研究主要讨论的是在电磁轴承出现磁极故障时重构及求解电流分配矩阵。实际上,随着故障的出现,由于磁极间的磁耦合以及电磁力的非线性,使得磁极上的电磁力和电流不一定有良好的线性关系,这就给转子的悬浮带来了一定的影响。此外,当前容错控制的磁极结构只是把传统差动控制的C型磁极结构断开,从而实现8个磁极的独立驱动。差动控制因为需要两边对称,减少相邻磁极对之间磁耦合以方便控制,磁极的数量一般为8极或8的倍数,这就使得定子结构的设计有了很大的局限性。而容错控制的定子结构并不需要像差动控制那样有严格的要求,磁极数量只需要为偶数即可。
为了分析电磁轴承有磁极故障时强耦合(NSNS型)和弱耦合(NNSS型)结构电磁轴承对转子稳定悬浮的影响,本文通过在Ansoft软件上搭建8磁极电磁轴承模型,仿真得到这两种结构下电磁轴承的磁力线分布图以及磁密分布图,从而对比分析两者对转子稳定悬浮的影响。本文还通过搭建不同磁极数量的电磁轴承进行仿真,获得气隙中的磁密度分布图,并通过分析不同磁极数量的定子结构对漏磁的影响,研究提高电流利用率的方法。
1 强耦合和弱耦合电磁轴承电磁力计算
1.1 电磁轴承磁路关系式
以8磁极异极型支承结构的主动电磁轴承为模型,以单自由度模型电磁力线性化为原型,推导出NSNS型和NNSS型结构电磁轴承的电磁力的偏流线性化过程。8磁极异极型支承结构的电磁轴承一般根据全N型磁极结构来搭建基本磁路关系式,再根据磁路原理推导出其它拓扑结构电磁轴承的磁路关系式。根据图1所示的全N型8磁极电磁轴承模型及等效磁路,具体的推导过程如下文所述。

图1 全N型轴承模型及等效磁路Figure 1. N-type AMB model and magnetic circuit
根据图1所示的等效磁路,由安培环路定律可计算出全N型支承结构电磁轴承的磁路方程如式(1)所示。
(1)
基于基尔霍夫定律在主动电磁轴承系统中的应用,相应结点处的磁通代数和如式(2)所示,通常为固定值0。
φ1+φ2+φ3+φ4+φ5+φ6+φ7+φ8=0
(2)
把式(1)和式(2)联立起来,然后改写成矩阵的形式以方便计算,式(3)为

(3)
令φ=[φ1φ2φ3φ4φ5φ6φ7φ8]T,I=[i1i2i3i4i5i6i7i8]T,


则式(3)可以化简为Rφ=NI。当电磁轴承的拓扑结构与图1中的排列方式不相同时,就可以引入K矩阵来描述不同拓扑结构电磁轴承实际的方向,即I=KId。其中,Id表示实际电流矩阵。NNSS型和NNSS型拓扑结构可以分别表示为

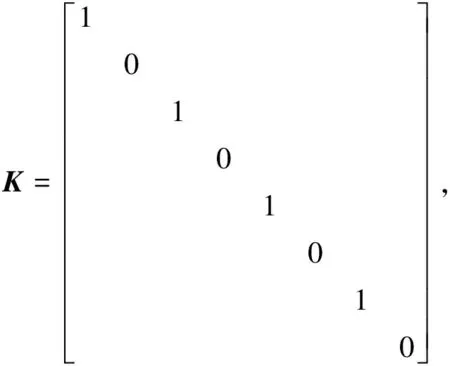
则不同拓扑结构的异极型支承结构的电磁轴承等效磁路关系式为Rφ=NKId。
1.2 电磁轴承电磁力计算
电磁轴承定子与转子间气隙的磁通量与磁感应强度有如下关系
[φ1φ2φ3φ4φ5φ6φ7φ8]T=S×[B1B2B3B4B5B6B7B8]T
(4)
式中,S为定子与转子相接触的磁极面积;Bj(j=1,2,3,…,8)为定子磁极面上的磁感应强度。则式(4)可改写为φ=SB。
将式(3)和式(4)的矩阵形式予以整合,可以得到RSB=NKId,则B=S-1R-1NKId。假设C=S-1R-1N,那么磁感应强度可表示为
B=CKId
(5)
而任意的一个定子磁极面上产生的电磁力可表示为
(6)
式中,μ0是定转子间气隙的真空磁导率;Idj为第j个定子上的绕组线圈的控制电流大小;N为系统中每一个定子上缠绕的线圈的数量;Xj是系统中转子与定子间气隙的长度。此时,8磁极异极型支承结构的主动电磁承轴定子中的转子在X和Y方向分别受到的电磁合力为
(7)
式中,θj(j=1,2, 3,…,8)为相对应定子的中心线与x轴正方向的上的夹角。如图1电磁轴承模型所示,根据文献[5]提到的偏流线性化方法就可以实现电磁力的线性化。此时可根据矩阵K,用MATLAB求解出NNSS和NSNS型两种结构的电流分配矩阵。
2 定子磁极故障磁场仿真及分析
8磁极电磁轴承理论上在最多有五路磁极故障时仍可继续工作。虽然通过文献[12]中提到的坐标变换法,由基本故障类型的电流分配矩阵计算可得相同磁极故障的电流分配矩阵,减少了数据的分析量,但基本的故障模型种类仍然较多。在实际的工程应用中,电磁轴承容错控制的目的并不是让电磁轴承在故障时继续工作,而是为了在磁极突然出现故障时,使其能够稳定降低速度,然后便于对故障磁极进行维修。维修可降低磁极同时故障的概率,所以可不考虑多个磁极故障的情况,只对单个以及两个磁极故障时的磁场分布进行仿真与分析。
2.1 电磁轴承模型对象
电磁轴承系统主要由定子、转子、线圈、功率放大器、位移传感器、控制器等几部分组成。本文通过有限元分析软件搭建模型进行仿真分析[18]。定子具体设计尺寸(单位:mm)如图2所示。所使用材料的具体型号为DW360_50,并在定子上缠绕100匝线圈,材料型号是copper。转子为圆形铁芯,直径22.4 mm,重量为9.92 kg,材料为Steel_1010。系统求解区域以及转子和定子之间0.4 mm的气隙采用的材料型号为Vacuum。

图2 定子的设计尺寸图Figure 2. Design dimension drawing of stator
2.2 单个磁极基本故障磁场分析
单个磁极故障是容错控制下最可能出现的情况,所以本文对该故障情况进行详细的分析。为了方便进行对比分析,所有的定子磁极上都使用相同幅度的静态电流,然后通过Ansoft软件进行仿真。
NNSS型拓扑结构电磁轴承在无磁极故障时,大部分磁力线会在磁极对中形成回路,且磁极对之间相互没有影响。而当一个磁极出现故障时,故障磁极两边的磁极会形成新的回路。如图3所示,有少量磁力线通过故障磁极本身,虽然其它磁极大部分磁力线仍然在原磁极对中形成回路,但在相邻磁极对之间有磁力线通过,说明磁极对之间相互有了耦合,给电磁轴承系统X和Y方向上电磁合力控制带来了影响。此时的磁通密度分布图如图3(b)所示。

(a) (b)图3 NNSS型单个磁极故障磁场分布图(a)NNSS型磁力线分布 (b)NNSS型磁通密度分布Figure 3. NNSS model single pole fault magnetic field distribution diagram(a)NNSS magnetic field lines distribution(b)NNSS magnetic flux density distribution
NSNS型拓扑结构在无磁极故障时,磁极产生的磁力线会与相邻磁极形成两个蝶形回路。而当其中一个磁极出现故障时,如图4(a)所示,与故障磁极相邻两边的正常磁极产生的磁力线,仅有少量磁力线通过故障磁极形成回路,大部分磁力线都会通过与另一侧的正常磁极形成回路。这就导致故障磁极相邻的两个磁极的磁通密度明显要比其它磁极的磁通密度要大。如图4(b)所示,另有一小部分磁力线会通过转子与其它非相邻的磁极形成新的回路,说明非相邻磁极之间产生了较强的耦合。
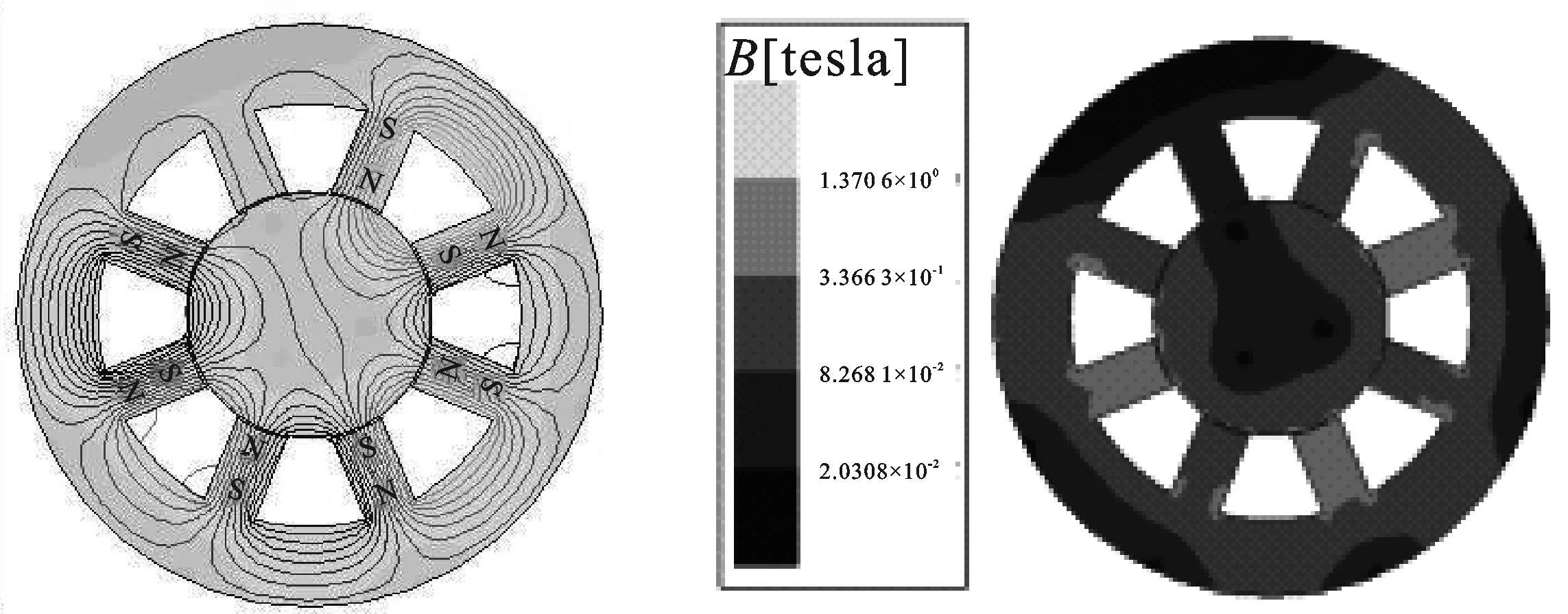
(a) (b)图4 NSNS型单个磁极故障磁场分布图(a)NSNS型磁力线分布 (b)NSNS型磁通密度分布Figure 4. NSNS model single pole fault magnetic field distribution diagram(a)NSNS magnetic field lines distribution (b)NSNS magnetic flux density distribution
2.3 两个磁极基本故障磁场分析
2.3.1 第一和第二两个磁极基本故障
对于NNSS型拓扑结构的电磁轴承,当第一和第二两个磁极同时出现故障时的磁场分布包括两种情况:(1)两个故障磁极出现在同一个磁极对中。磁力线分布如图5(a)所示,此时磁力线仍然在原磁极对之间形成回路,但是相邻磁极对之间有了较强的耦合;(2)两个故障磁极出现在相邻两个磁极对中。如图5(b)所示,此时原本与故障磁极形成磁极对的磁极产生的磁力线,一部分与故障磁极形成回路,一部分与另一侧的正常磁极形成回路。从图中可知,非同磁极对故障时,磁极间的耦合程度比同磁极对故障更为复杂。

(a) (b)

(c)图5 第一和第二个磁极故障磁场分布图(a)NNSS型同磁极对故障 (b)NNSS型非同磁极对故障(c)NSNS型磁极故障Figure 5.The first and second magnetic pole fault magnetic field distribution diagram(a)NNSS co-pole pair fault (b)NNSS non-co-polepair fault (c)NSNS type pole fault
而对于NSNS型拓扑结构的电磁轴承,当第一和第二两个磁极同时出现故障时的磁场分布只有一种。如图5(c)所示,此时与故障磁极相邻的两个磁极的磁力线的一部分会与另一侧的正常磁极形成回路,另一部分会跨过两个故障磁极,相互之间形成新的回路。两个磁极间距较大导致漏磁现象更为明显,而其余的磁极仍然按照原本的规律分别与相邻的两个磁极形成回路。
2.3.2 第一和第三两个磁极基本故障
当第一和第三两个磁极同时出现故障时的磁场分布如图6所示。
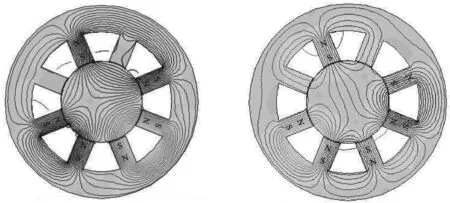
(a) (b)图6 第一和第三两个磁极故障磁场分布图(a)第一和第三磁极故障时NNSS型磁力线分布(b)第一和第三磁极故障时NSNS型磁力线分布Figure 6.The first and third magnetic pole fault magnetic field distribution diagram(a)NNSS type magnetic field line distribution under the first and third magnetic poles fault (b)NSNS magnetic field line under the first and third magnetic poles fault
图6(a)为NNSS的磁场分布,故障磁极两边的磁极产生的磁力线会跨过故障磁极形成新的回路,其它磁极的磁力线仍然按照原规则形成回路,但是磁极对之间有了明显的耦合。NSNS结构的两个故障磁极中间的磁极产生的磁力线主要通过两个故障磁极形成回路。如图6(b)所示,一部分磁力线会通过转子与其他磁极产生耦合。而两个故障磁极另一侧的磁极产生的磁力线主要和相邻正常磁极形成回路,其它磁极仍然按照原规则形成回路,磁力线耦合情况比较复杂。
2.3.3 第一和第四两个磁极基本故障
NNSS型第一和第四磁极出现故障情况如图7(a)所示。故障磁极两边正常磁极产生的磁力线会跨过故障磁极相互间形成新的回路,仅有一小部分磁力线会通过故障磁极形成回路,磁极间的耦合复杂。NSNS拓扑结构故障磁极基本没有磁力线通过,如图7(b)所示,剩余的6个磁极会两两一对形成3个磁极对,有一小部分磁力线会在相邻磁极对以及转子中通过,产生一定程度的耦合。
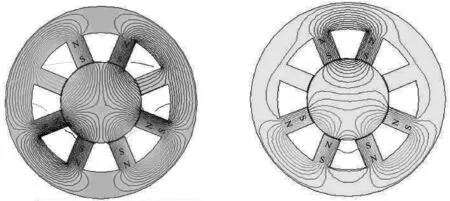
(a) (b)图7第一和第四两个磁极故障磁场分布图(a)第一和第四磁极故障时NNSS型磁力线分布(b)第一和第四磁极故障时NSNS型磁力线分布Figure 7.The first and fourth magnetic pole fault magnetic field distribution diagram(a)NNSS magnetic field line distribution under the first and fourth magnetic poles fault (b)NSNS magnetic field line under the first and fourth magnetic poles fault
2.3.4 第一和第五两个磁极基本故障
图8(a)为NNSS在第一和第五磁极同时出现故障下时的磁场分布,其磁场分布情况与上一种故障情况相似,磁极间的耦合也比较复杂。NSNS在该故障条件下的磁场分布如图8(b)所示,此时磁力线基本按照原规则分别与两边的磁极各形成一个回路。但由于强耦合原因,大部分磁力线都与正常磁极形成回路,仅很少一部分磁力线会通过故障磁极。
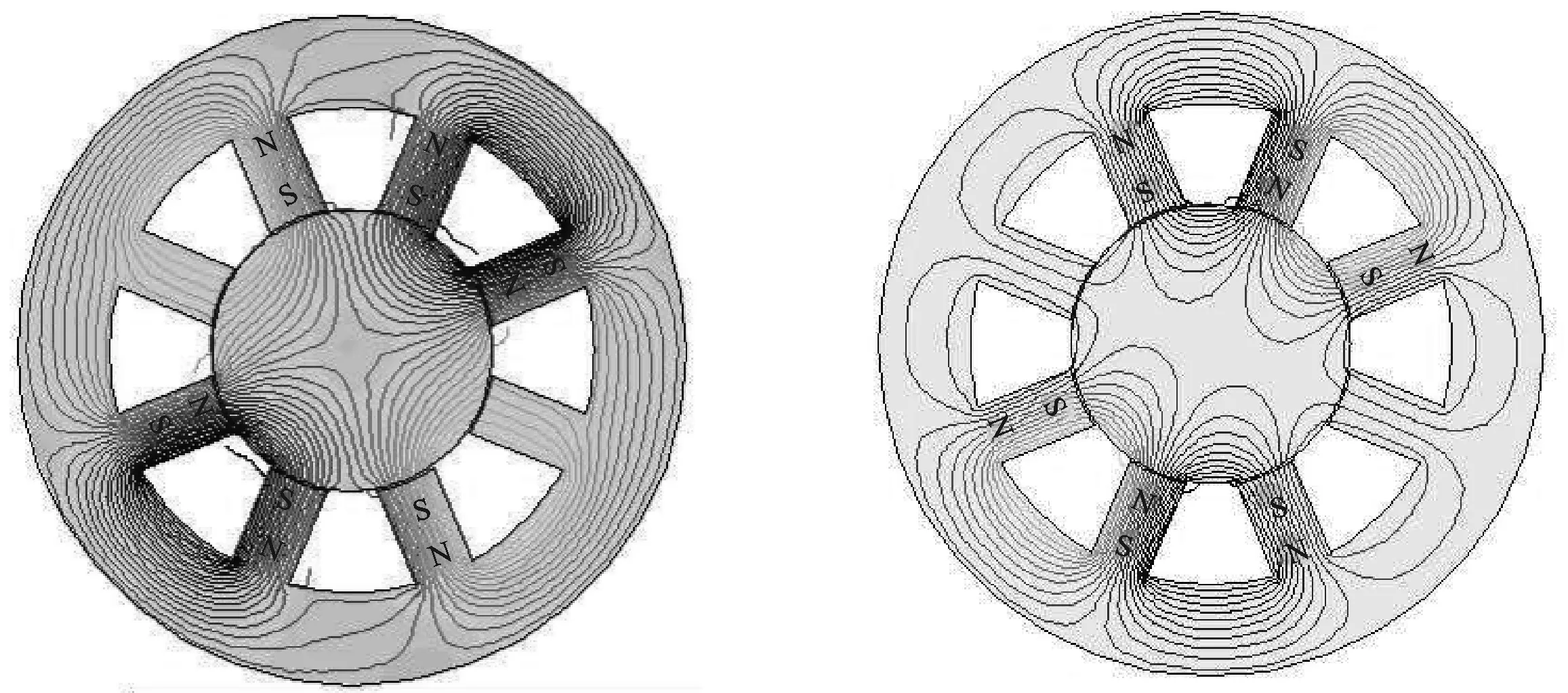
(a) (b)图8 第一和第五两个磁极故障磁场分布图(a)第一和第五磁极故障时NNSS型磁力线分布(b)第一和第五磁极故障时NSNS型磁力线分布Figure 8.The first and fifth magnetic pole fault magnetic field distribution diagram(a)NNSS magnetic field line under the first and fifth magnetic poles fault (b)NSNS magnetic field line under the first and fifth magnetic poles fault
3 定子结构对漏磁的影响
根据电磁轴承磁场仿真结果可以看到,有部分磁力线因未通过磁极面而产生漏磁,所以定子结构对漏磁有较大的影响。为了提高NSNS型拓扑结构电磁轴承电流转化为电磁力的效率,本文搭建了4、6、8、10、12和14磁极的电磁轴承模型,磁极均匀分布在定子上。本文所使用的电磁轴承模型被缠绕相同规格和方向的100匝线圈模型,并根据NSNS拓扑结构的要求在各个磁极上接通幅度为1 A的静态电流。
根据式(5),理论上1 A电流在电磁轴承磁极面上可产生的磁通密度为310.525 mT。通过与仿真时得到的电磁轴承定子和转子间气隙中的磁通密度实际值进行计算,可以得到电磁轴承的电流利用率,结果如表1所示。

表1 不同磁极数量电磁轴承电流利用率
从表1可知,随着磁极数量的增加,电磁轴承定子和转子间气隙中的磁通密度逐渐增大,电流的利用率逐渐增加,增速随着磁极数量的增加而逐渐减小。当磁极数量增加到12极时,电流利用率超过99%,此时随着磁极的增加,电流利用率提高的效果逐渐趋于平缓。电磁轴承主要通过控制磁极端面上的电磁力控制转子悬浮,理论上磁极数量越多,定转子间的接触面越大,转子的悬浮性能会越好。但在实际的电磁轴承定子结构设计过程中,磁极数量越多,定子结构越复杂。由于每个定子上都需要缠绕几十匝线圈,给建造带来较大的困难和成本。而且磁极数量增加,必然使得控制器需要处理更多的数据,增加了控制器控制转子稳定悬浮的难度。因此在实际的工程应用中,需要选择合适的磁极数量,使漏磁率达到一定的工业标准即可。
4 结束语
本文通过Ansoft软件对强耦合和弱耦合结构电磁轴承在单个和两个磁极故障时的磁场分布情况,以及不同磁极数量电磁轴承的漏磁情况进行仿真分析。通过仿真分析可得出如下结论:强耦合和弱耦合结构电磁轴承随着故障磁极位置的改变,耦合情况复杂多变,具有各自的优缺点。弱耦合结构电磁轴承主要通过定子形成耦合,而强耦合结构电磁轴承的耦合主要存在于转子上,且随着磁极数量的增加可有效减少电磁轴承漏磁现象,从而提高电流的利用率。

