基于灰色模型的乙酸乙烯酯顶空进样质量不确定度评定

张霞，李国智，龙雨蛟，李勤书，徐淑浩，陈杰，朱雪峰，杨冬梅

[红云红河烟草（集团）有限责任公司红河卷烟厂，云南弥勒 652300]

顶空进样与气相色谱联用技术已被广泛应用于食品、环境、医疗卫生等各领域产品质量控制及科学研究中［1］。静态顶空气相色谱法的关键技术是顶部空间的取样环节［2］，顶空进样质量是直接影响方法检出限和检测结果准确性的重要因素之一。顶空进样质量不确定度越小，检出限重复性的不确定度越小，检测结果与其真值也越接近。近年来，不确定度已经被作为衡量检测结果可靠性的重要指标，而对于顶空进样器进样质量测定过程的不确定度评定未见报道。目前化学工作者主要采用统计学方法评定化学检测重复性引入的不确定度［3-6］。统计学方法的应用前提是测量数据足够多，且明确其统计分布规律，而实际的测量过程中较难同时满足这些要求，故采用传统的统计学方法计算较为准确的测量不确定度具有一定的局限性［7］。

邓聚龙［8］于1982 年首创灰色系统理论，该理论对样本量没有严格要求，数据不需服从任何分布，它是利用“部分信息已知、部分信息未知”的小样本、贫信息等不确定性系统作为研究对象，来预测系统的未知信息，将“灰色系统”白化。灰色预测模型是灰色系统理论的重要内容，在工业、农业、地质、气象、经济等领域已经得到成功应用。许多学者已将灰色系统理论用于测量不确定度的评定［9-16］。

在化学分析检测过程中，标准物质本身的不确定度、测量仪器和检测环境的不完善等因素，导致测量值产生一定的不确定性，可将化学分析检测过程视为灰色系统测量过程［12］。

笔者依据静态顶空相平衡基本原理［17-20］，测定由顶空导入气相色谱柱的乙酸乙烯酯实际进样质量，基于灰色系统理论，并借鉴JJF 1059.1—2012《测量不确定度评定与表示》［21］相关要求，建立了不确定度的灰色评定数学模型，对样本量小、数据分布规律未知的顶空实际进样质量的不确定度进行评定。

1 实验部分

1.1 主要仪器与试剂

顶空进样器：G1888 型，美国安捷伦科技有限公司。

气相色谱仪：HP 6890 型，配有FID 检测器及化学工作站，美国安捷伦科技有限公司。

电子封盖器和启盖器：用于20 mm 盖，带锂电池，美国安捷伦科技有限公司。

顶空瓶：20 mL，美国安捷伦科技有限公司。

分析天平：AB104-S 型，感量为0.1 mg，瑞士梅特勒-托利多公司。

乙酸乙烯酯：色谱纯，德国埃伦斯托弗博士公司。

N，N-二甲基甲酰胺：分析纯，四川西陇化工有限公司。

1.2 溶液配制

按YC／T 267-2008 《烟用白乳胶乙酸乙烯酯的测定 顶空-气相色谱法》［22］技术要求，以乙酸乙烯酯为顶空进样质量不确定度评定的挥发性成分标准物质，N，N-二甲基甲酰胺为溶剂。

乙酸乙烯酯标准储备溶液：400 mg／L，称取约0.020 0 g（精确至0.1 mg）乙酸乙烯酯于50 mL 容量瓶中，用N，N-二甲基甲酰胺稀释并定容至标线，混合均匀。

系列乙酸乙烯酯标准溶液：用N，N-二甲基甲酰胺逐级稀释上述乙酸乙烯酯标准储备溶液，配制成乙酸乙烯酯的质量浓度分别为64.00、25.60、10.24、4.096、1.638 mg／L 的系列标准工作溶液。

1.3 静态顶空-气相色谱-FID 仪器工作条件

按YC／T 267—2008 《烟用白乳胶乙酸乙烯酯的测定 顶空-气相色谱法》［22］执行。

1.4 实验方法

1.4.1 测定原理

在一定温度的密闭容器中，试样中的挥发性组分在气相（顶空）和基质（液相或固相）之间存在分配平衡，将挥发性组分在气液两相中浓度之比定义为气液分配常数。根据质量平衡方程、气液分配常数及气相色谱定量原理，可推导出气液非等体积条件下静态顶空分析的两次相平衡原理［17］及气液分配常数［17～20］基本关系式：

式中：K——气液分配常数；

A1——第一次相平衡时，气相色谱仪测定的气相中挥发性组分色谱峰面积；

A2——第二次相平衡时，气相色谱仪测定的气相中挥发性组分色谱峰面积；

R——液气相比，R=VL／Vg（VL、Vg分别为液、气相体积）。

ρ0——液相中挥发性组分的初始质量浓度；

ρg1——第一次相平衡时气相中挥发性组分质量浓度。

由式(1)和(2)可知，在同一平衡、色谱条件下，同一体系样品通过两次相平衡测定挥发性组分的气液分配常数K，就可以计算气相中挥发性组分的质量浓度，再根据顶空定量环体积和气相色谱分流／不分流进样口分流比，计算由顶空导入气相色谱检测器的挥发性组分进样质量。

1.4.2 测定过程

按照1.3 仪器工作条件，准确移取1.00 mL 质量浓度为1.586 1 mg／L 的乙酸乙烯酯标准溶液，置于20 mL 顶空瓶中，迅速密封瓶口，进行第一次顶空相平衡并测定乙酸乙烯酯色谱峰面积；待第一次顶空相平衡测定完毕及顶空瓶温度降至室温后，更换顶空瓶盖重新密封，进行第二次顶空相平衡并测定乙酸乙烯酯色谱峰面积；分别连续测定10 次，记录每次顶空两次相平衡测得的乙酸乙烯酯色谱峰面积，按式(1)计算乙酸乙烯酯在顶空相平衡过程中的气液分配常数K值，按式(2)计算乙酸乙烯酯标准溶液在顶空相平衡时气相中乙酸乙烯酯的质量浓度ρg1，再根据顶空定量环为3 mL、气相色谱分流／不分流进样口分流比（1∶20）、顶空液气相比R（1∶19），计算由顶空导入FID 检测器的乙酸乙烯酯实际进样质量。

2 顶空进样质量不确定度的灰色评定数学模型

参考灰色系统理论［8-10］，分析理想状态和实际状态下的测定过程，建立挥发性组分的顶空进样质量不确定度的灰色评定数学模型。

2.1 理想状态下顶空进样质量测定过程

在理想状态下，每一次测定值均为真值，不存在检测误差，则理想状态下挥发性组分的顶空进样质量测定值数列：

式中：x(1)(n)——累加的测定值。

在理想状态下，将挥发性组分顶空进样质量测定次数i作为横坐标，x(1)(i)作为纵坐标进行线性拟合，可得x(1)(i)与i的关系直线L，该直线经过原点(0，0)和点[n，x(1)(n)]。

2.2 实际状态下顶空进样质量测定过程

在实际状态下，挥发性组分顶空进样质量重复测定过程中，因受环境、仪器和测定方法等各种因素的影响，使测定值存在误差，每一次测定值均接近真值，且在真值上下波动。剔除测定值中的异常离群值后，将测定值按由小到大顺序排列，得到实际状态下挥发性组分顶空进样质量测定值数列：

若将挥发性组分的顶空进样质量测定次数i作为横坐标，将前n项的和y(1)(i)作为纵坐标，进行线性拟合，可得y(1)(i)与i关系曲线S。

2.3 测定分散性

当取相同的测定次数（横坐标值）时，曲线S 和直线L 的顶空进样质量测定值（纵坐标值）存在差异，此差异是由“人机料法环”等多种影响因素的存在所导致，反映了在重复测定过程中挥发性组分顶空进样质量的分散性。以曲线S 和直线L 之间沿纵坐标轴方向的距离Δ(i)表征误差的累加值：

2.4 测定重复性不确定度

当最大距离Δmax越大时，实际的挥发性组分顶空进样质量测定值就越分散，其标准差越大，测定重复性不确定度也越大。用sGrey表示挥发性组分顶空进样质量测定值的分散程度，按式(11)计算：

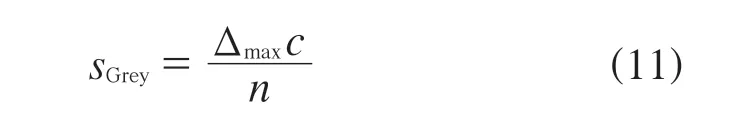
式中：Δmax——理想状态测定过程和实际状态测定过程的最大分散性；

c——灰色常系数；

n——测定总次数。

朱坚民［9］计算了4 种典型分布的灰色常系数c，分别为正态分布（c=2.50）、三角分布（c=2.45）、瑞利分布（c=2.41）和均匀分布（c=2.35），分布类型与灰色常系数关联性较小，即灰色理论评定模型对测量数据分布的依赖性较小。

参考JJF 1059.1—2012 《测量不确定度评定与表示》［21］中标准不确定度A 类评定，挥发性组分顶空进样质量灰色不确定度按式(12)计算：

3 乙酸乙烯酯顶空进样质量不确定度评定

3.1 乙酸乙烯酯顶空进样质量测定

按照1.4.2 测定方法，乙酸乙烯酯标准溶液的初始质量浓度ρ0=1.586 1 mg／L，顶空定量环为3 mL，分流比为1∶20，顶空液气相比R为1∶19，依次计算气液分配常数K值和顶空导入FID 检测器的乙酸乙烯酯实际进样质量。按从小到大的顺序将顶空进样质量测定结果列于表1。

表1 两次相平衡乙酸乙烯酯气液分配常数和顶空进样质量测定结果

3.2 不确定度的灰色评定

基于灰色模型评定方法，根据表2 数据，由式(9)计算得Δmax=0.168 81 ng。

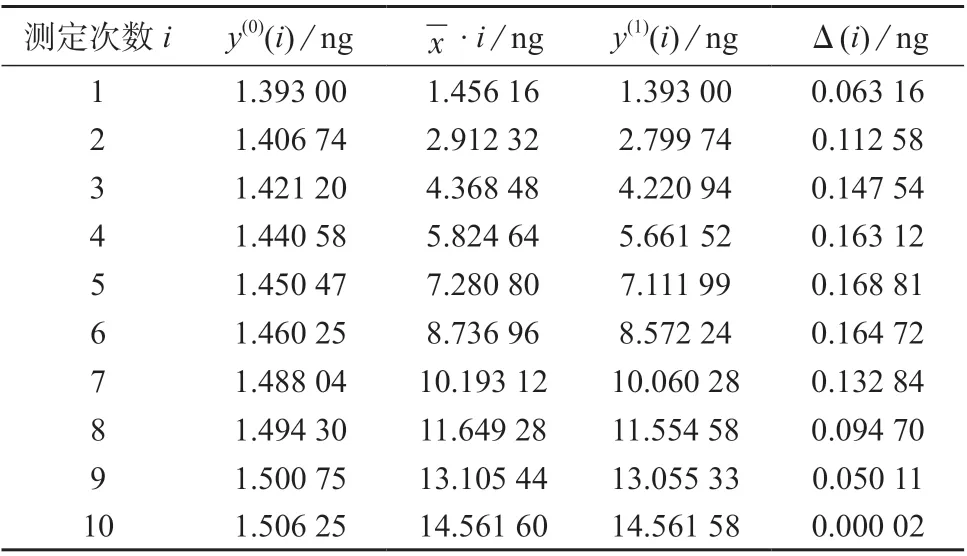
表2 乙酸乙烯酯顶空进样质量不确定度的灰色计算结果

若用式(10)计算Δmax，表2 中仅前5 组测定值小于算术平均值，则：

对比上述两种计算方法可知，式(9)和式(10)计算所得分散性结果吻合。然而按式(9)计算分散性Δmax过程繁琐，而按式(10)计算方法，得出顶空进样质量的算术平均值后，仅用小于平均值的5 组测定值即可计算得到Δmax，进而快速评定顶空进样质量的不确定度。

3.3 不同评定方法对比

3.3.1 贝塞尔公式法评定不确定度

假设乙酸乙烯酯顶空进样质量重复性测定值符合统计学正态分布，根据JJF 1059.1—2012 《测量不确定度评定与表示》［21］中标准不确定度A 类评定，其计算方法有贝塞尔公式法和极差法。通常情况下，当测定总次数n＜10 时，用极差法；当测定总次数n≥10 时，用贝塞尔公式法，因此采用贝塞尔公式计算重复测量标准差、A 类不确定度。

重复测量标准差按式(13)计算：

贝塞尔公式法标准不确定度计算结果见表3。

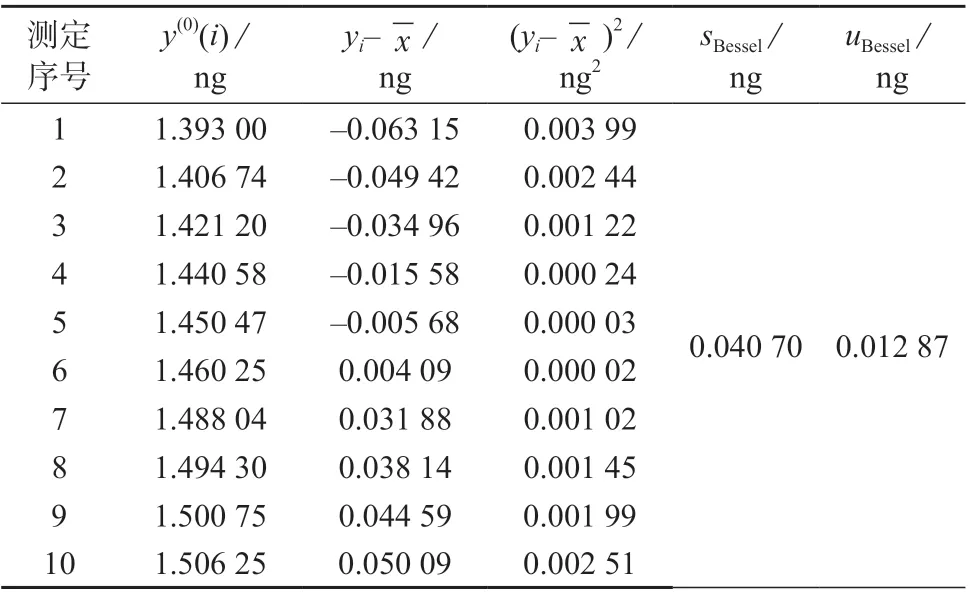
表3 贝塞尔公式法标准不确定度计算结果

3.3.2 不同评定方法比较

灰色模型与贝塞尔公式计算的不确定度结果对比见表4。由表4 可知，灰色模型计算的标准差、不确定度与贝塞尔公式计算结果无显著差异，两种方法标准不确定度的相对偏差为3.65%，表明灰色模型可用于乙酸乙烯酯顶空进样质量不确定度的评定。

表4 灰色模型与贝塞尔公式法评定不确定度结果对比

4 结语

通过两次相平衡分析法测定乙酸乙烯酯顶空进样质量，建立灰色理论数学模型，对YC／T 267—2008 《烟用白乳胶中乙酸乙烯酯的测定 顶空-气相色谱法》［22］中乙酸乙烯酯顶空进样质量重复测定值的标准差和不确定度进行评定。比较了灰色模型和统计学方法评定的标准差和不确定度，评定结果相近，无显著差异。作为非统计学方法的灰色模型，可对数据量小、分布规律未知的乙酸乙烯酯顶空进样质量不确定度进行评定，该方法科学，计算简便，结果可靠。