基于改进Johnson-Cook模型的Mg-Gd-Y-Zn-Zr合金高温流变行为研究

刘 畅 陈小敏 陈书涵 陈建兵

1. 长沙理工大学

创新创业教育学院

湖南 长沙 410114

2. 长沙理工大学

汽车与机械工程学院

湖南 长沙 410114

0 引言

镁合金以其较低的密度、优越的阻尼特性、较高的比强度等特点，在航空航天、电子、交通运输等领域得到了广泛应用[1-2]。镁合金的加工和强化主要依靠热塑性变形，经过塑性加工后得到的变形镁合金，其综合性能可以得到显著提升[3-5]。因此，镁合金的热变形规律及其热加工工艺优化具有十分重要的研究价值。

本构模型是描述金属材料加工变形规律的一种数学模型，能够定量分析金属材料热变形的流动应力与各变形参数之间的关系[6-7]。根据模型建模思想的不同，可将金属材料本构关系模型大致分为唯象学模型、物理基模型和人工神经网络模型[8]。在唯象学本构模型中，较为常用的有Zerilli-Armstrong（Z-A）模型[9]、Arrhenius-Type模型[10]和 Johnson-Cook模型等。其中Johnson-Cook模型考虑了材料在实际加工过程中，影响材料流动应力大小的3种主要因素，因而得到了广泛的应用[11]。Lin Y. C. 等[12]通过单轴拉伸试验研究了一种高强合金的热变形行为，并建立了描述合金流变应力与应变速率以及变形温度关系的Johnson-Cook模型。Jia Z. 等[13]研究了AA6016-T6合金，在0.001～100 s-1应变速率下的动态力学性能及断裂特征，建立了反映应变速率影响的修正Johnson-Cook模型。A. Shokry等[14]总结了不同动态加载条件下4种类别合金的应力-应变关系，提出了一种改进的通用Johnson-Cook模型（PMJC模型），并对模型的准确性进行了验证。改进的Johnson-Cook模型都是选取参考温度和应变速率下的应力-应变关系作为基准，再综合考虑其它变形条件下的应力变化情况，最后得到能够适用于所有变形参数下的流变应力本构方程[15]。因此，改进的Johnson-Cook模型可以准确预测不同变形条件下各类金属的流变应力，但应用于稀土镁合金热变形行为的研究较少。

本文以实验室制备的Mg-Gd-Y-Zn-Zr合金为研究对象，借助恒温等应变速率高温拉伸实验，研究该合金的热变形行为。基于其不同变形条件下的真应力-真应变曲线，建立了一种改进的Johnson-Cook模型，以期为Mg-Gd-Y-Zn-Zr合金的加工工艺参数优化，以及有限元数值模拟提供模型基础。

1 实验

1.1 实验材料与实验仪器

实验材料为Mg-5.5Gd-4.4Y-1.1Zn-0.5Zr合金，由长沙理工大学实验室制备。

热模拟试验机，Gleeble-1500，美国DSI公司。

1.2 实验过程

在400 ℃的温度下将Mg-5.5Gd-4.4Y-1.1Zn-0.5Zr合金挤压成 Ф400 mm的棒材，并根据ISO 783—1999《金属材料高温拉伸试验》标准，加工成标准试样。利用Gleeble-1500热模拟试验机进行高温拉伸实验，变形参数设置：温度分别为250, 300, 350, 400℃，应变速率分别为0.001, 0.01, 0.1, 1 s-1。先将试样以10 ℃/s的速率加热至所设置的拉伸实验温度，保温3 min后开始加载；将试样以恒定的温度和应变速率拉伸直到断裂。

2 实验结果与分析

2.1 应力应变曲线分析

图1为高温拉伸实验得到的Mg-Gd-Y-Zn-Zr合金的真应力-真应变曲线。

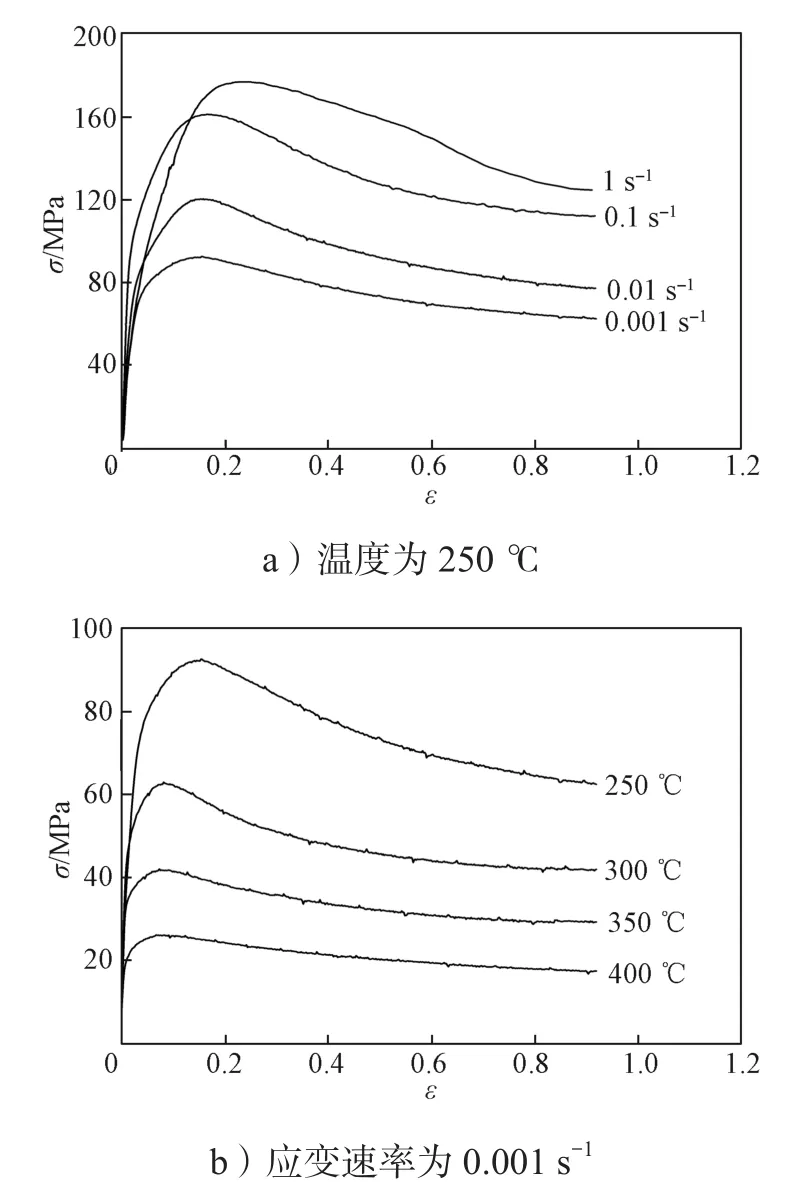
图1 合金的真应力-真应变曲线Fig. 1 True stress-true strain curve of the alloy

由图1可知，分别在变形温度T=250 ℃以及应变速率= 0.001 s-1的变形条件下，Mg-Gd-Y-Zn-Zr合金的流变应力曲线全部呈现出大致相同的变化趋势，应变、变形温度和应变速率均显著影响流变应力的大小。在变形初始阶段，受加工硬化作用的影响，合金的流变应力快速增大；随着应变的增加，累积的变形储能加快了动态再结晶的进行，导致流变应力在达到峰值之后趋于稳定。各变形条件下的流变曲线均在应变ε=0.2之后进入流变稳态阶段。由于本构方程描述的是材料在稳态流变阶段的流变应力与温度、应变速率等因素的关系，因此本文选取应变ε在0.2～0.8范围内的实验数据作为建模依据。

2.2 Johnson-Cook 模型

Johnson-Cook模型认为在金属材料塑性变形过程中，其流变应力的大小主要受应变速率硬化、应变硬化与热软化的影响。因此，该模型将应变速率、应变和变形温度3种参数分别引入到方程中，其形式为

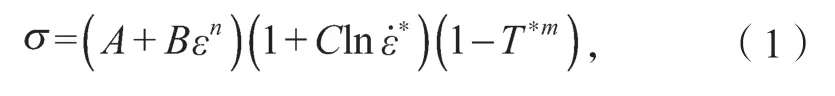
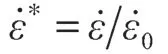
原始的Johnson-Cook模型（式（1））参数较少，且都具有明确的物理意义，计算方便。但原始的 Johnson-Cook模型仅能在参考应变率和参考温度下才显示出良好的预测结果。其主要原因是原始模型假设了应变硬化、应变速率硬化和热软化是3个不相关的因素，忽略了应变、应变速率和变形温度之间的相互影响。

2.3 改进的Johnson-Cook 模型

基于原始的Johnson-Cook模型，并针对材料热塑性变形过程中温度、应变速率与应变3种影响因素的耦合效应，对模型进行改进。改进后的模型为

式中A1、B1、B2、B3、C、λ1、λ2均为无实际物理意义的材料常数。

分别选取 250 ℃（523 K）和 0.001 s-1作为改进的 Johnson-Cook 模型的参考变形温度和参考应变速率。当变形温度和应变速率均取参考值时，可以将式（2）改写为

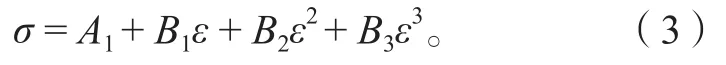
通过对参考温度和参考应变速率下的应变、应力值进行多项式拟合，可求得拟合曲线各项的系数，即为模型（3）各参数A1、B1、B2、B3的值，如图 2 所示。

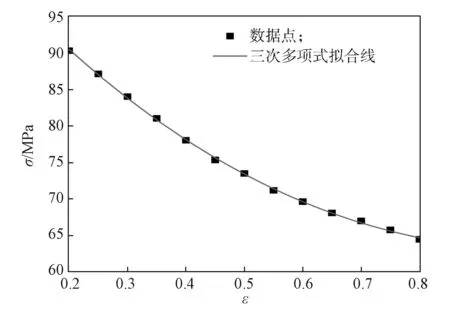
图2 参考温度和参考应变速率下流变曲线的多项式拟合Fig. 2 Polynomial fitting of rheological curves at reference temperature and reference strain rate

当T=250 ℃（523 K）时，式（2）改写为

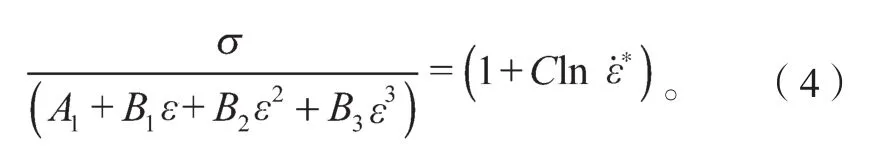
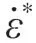
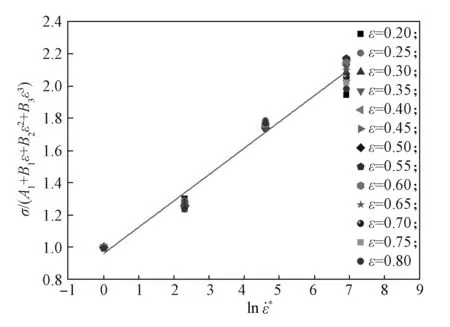
图3 参考变形温度下 σ/(A1 + B1ε + B2ε2 + B3ε3)与ln 的线性关系Fig. 3 The linear relationship between σ/(A+ Bε + Bε2 +1 12 B3ε3) and lnat the reference deformation temperature

令λ=λ1+λ2ln，λ是与应变速率相关的材料常数，对于给定的应变速率，λ可以被看作是一个定值。式（2）可改写为

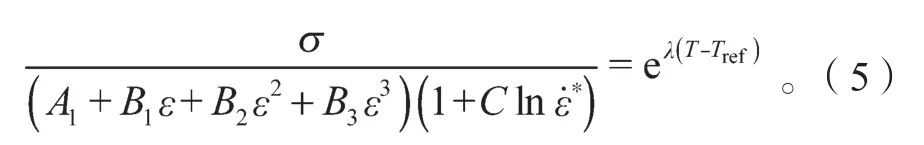
对式（5）两边取自然对数得

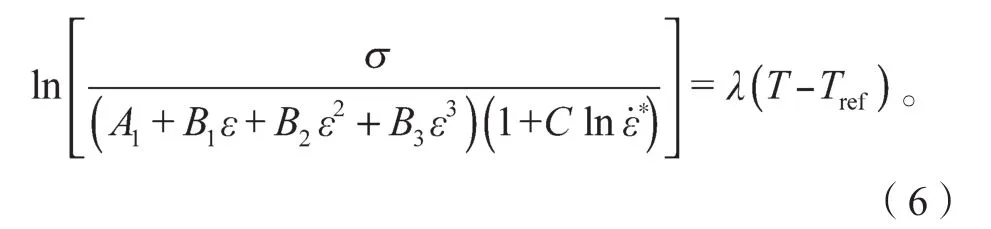
根据实验数据，本文可以得到不同应变速率下，ln{σ/[(A1+B1ε+B2ε2+B3ε3)(1+Cln)]}与T-Tref的数据点，并将其进行线性拟合，结果如图 4 所示。

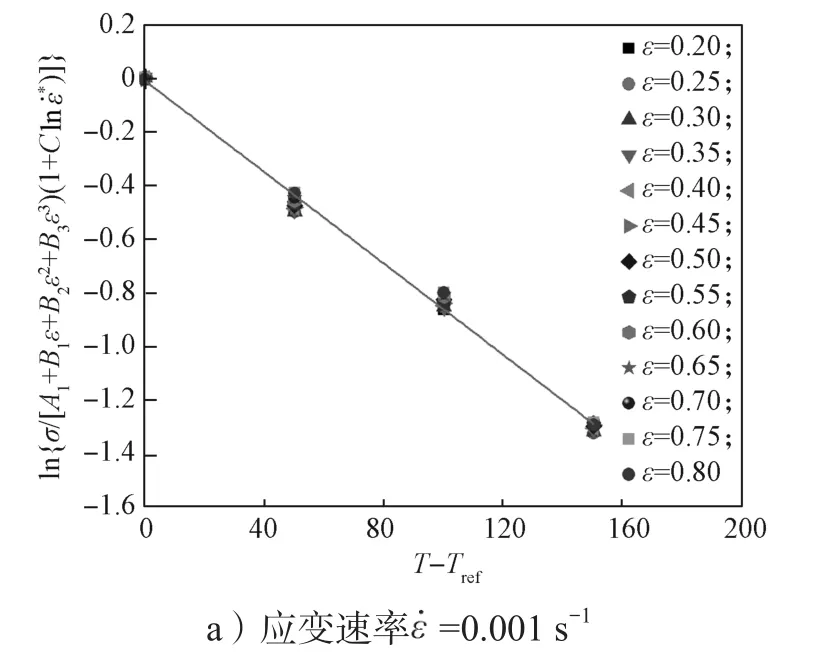
图4 不同应变速率下 ln{σ/[(A1 + B1ε + B2ε2 + B3ε3)·(1+Cln )]}与T-Tref的线性关系Fig. 4 Linear relationship between ln{σ/[(A1 + B1ε + B2ε2 + B3ε3)(1+Cln)]}and T-Tref at different strain rates

根据图4中的线性拟合关系，可以得到应变速率分别为 0.001, 0.01, 0.1, 1 s-1时模型（6）中参数λ的值，结果如表1所示。

根据表1中的数据描点，并进行线性拟合，结果如图5所示。根据λ与ln的拟合直线，可计算出λ1和λ2的值。

表1 不同应变速率下参数的取值Table 1 Values of parameter under different strain rates

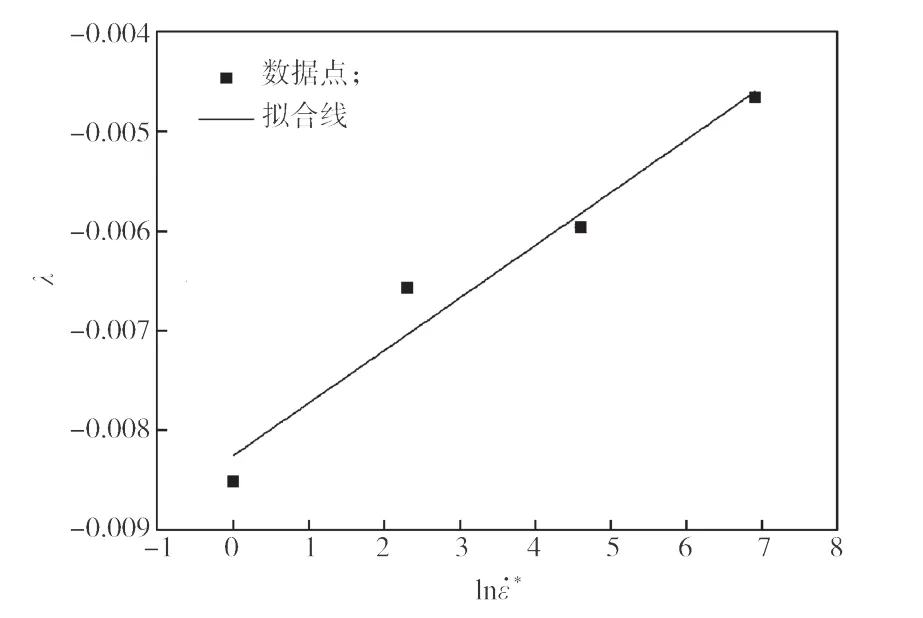
图5 λ 与 ln 的关系Fig. 5 The relationship between λ and ln

综上所述，可求得改进Johnson-Cook模型（式（2））的参数，如表2所示。

表2 改进Johnson-Cook模型的参数值Table 2 The parameter values of improved

2.4 模型预测精度分析

不同变形条件下，Mg-Gd-Y-Zn-Zr合金的流变应力，即改进Johnson-Cook模型的预测值与实验值，如图6所示。

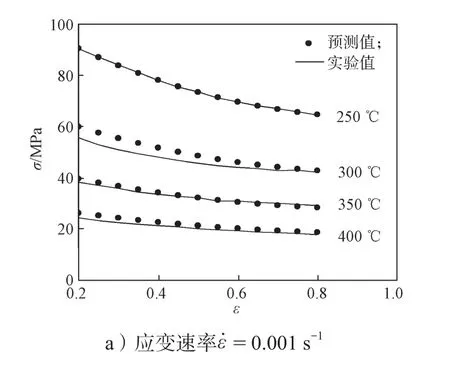
图6 不同变形条件下合金的流变应力模型预测值与实验值比较Fig. 6 Comparison of predicted value and experimental value of alloy flow stress under different deformation conditions

为了进一步评估改进模型的预测精度，特引入相关度（R）和平均相对误差（Δ）来定量分析[16]。相关度作为反映变量之间线性相关程度的指标，在这里用来表示改进模型预测值与实验值之间的符合程度。相关度高不一定表明预测值与实验值吻合准确，还有可能出现数值的偏离。平均相对误差指相对误差的平均值，在这里用来表示模型预测值与实验值的偏离程度。

相关度和平均相对误差的数学表达式为

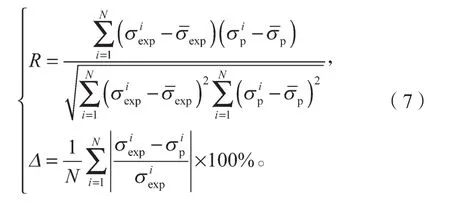
式中：σexp为热拉伸实验得到的流变应力值；

σp为改进Johnson-Cook模型的预测值；

N为选取的观测点数量。

将不同变形条件下的预测值与实验值代入式（7），并将二者在Origin软件中进行比较分析，所得结果如图 7 所示。

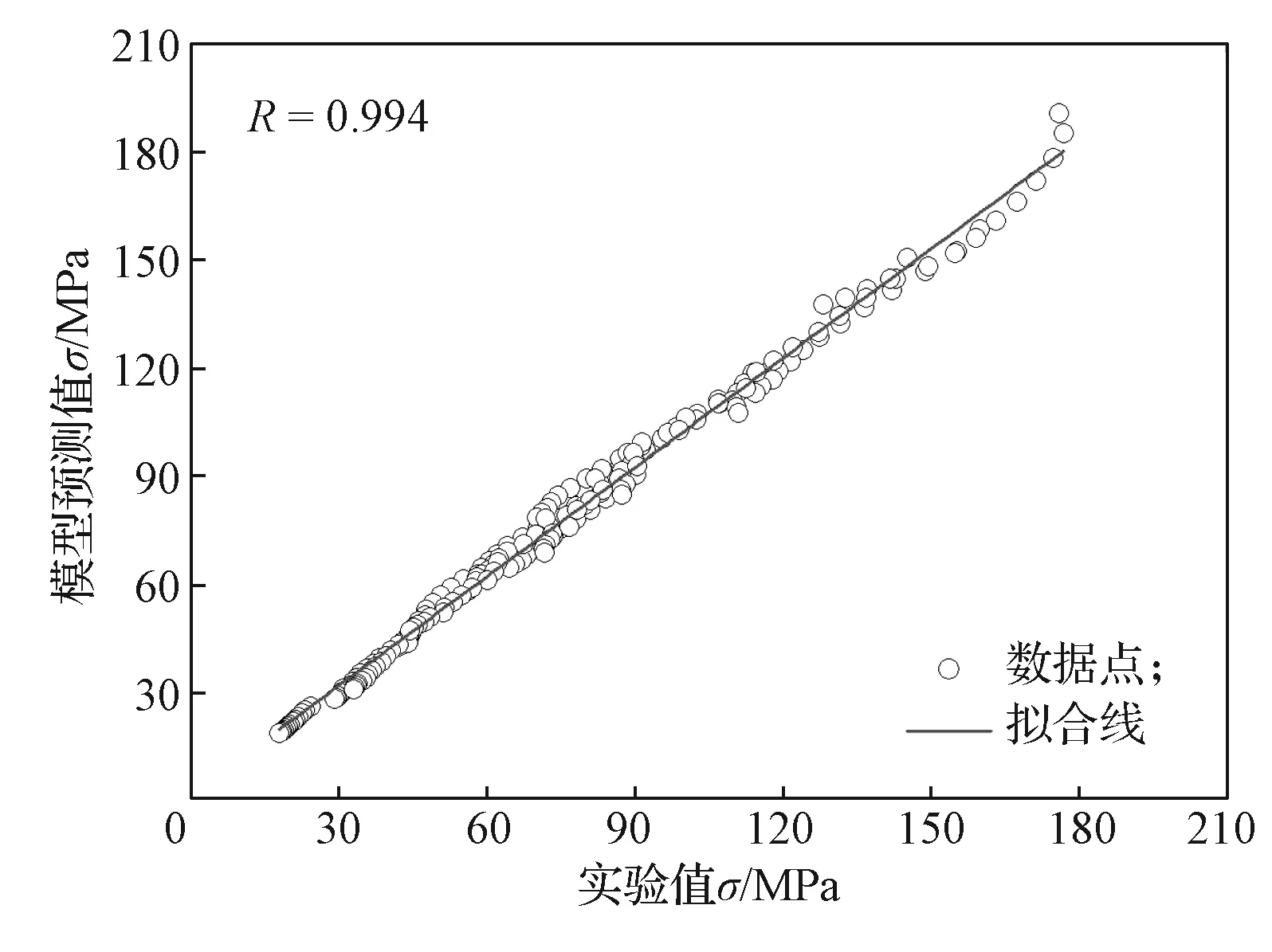
图7 改进模型的预测值与实验值的相关度Fig. 7 The correlation between the predicted value of the improved model and the experimental value

通过计算可得，改进Johnson-Cook模型的预测值与实验值的相关度为0.994，平均相对误差为4.5%，这表明该模型能够准确预测Mg-Gd-Y-Zn-Zr合金不同变形条件下的流变应力。

3 结论

综上所述，可得如下结论：

1）在Mg-Gd-Y-Zn-Zr合金高温变形过程中，应变速率的升高和变形温度的降低均会导致合金的流变应力明显升高。合金流变曲线显示出典型的动态再结晶软化机制，且在较高的变形温度（350, 400 ℃）及较低的应变速率（0.001, 0.01 s-1）下，动态再结晶软化效果明显。

2）基于实验得到的流变曲线，并综合考虑了热软化、应变速率硬化和应变硬化3种因素的影响，建立了Mg-Gd-Y-Zn-Zr合金改进的Johnson-Cook模型。将改进模型的预测值与实验值进行对比，可知模型预测值与实验值的相关度（R）达到了0.994，平均相对误差（Δ）只有4.5%，表明模型的精度较高，能够准确地描述和预测Mg-Gd-Y-Zn-Zr合金的高温流变应力。