滑模变结构控制在凹版印刷机中的应用

刘晓燕 杨 瑶 李秉晨

1.湖南铁路科技职业技术学院铁道工程与信息学院湖南 株洲 412006

2. 湖南中医药高等专科学校护理系湖南 株洲 412012

3. 湖南工业大学轨道交通学院湖南 株洲 412007

0 引言

凹版印刷机是包装印刷行业的重要设备之一[1]。尽管我国在1990年就生产了第一台具有自主知识产权的凹版印刷机[2]，然而我国凹版印刷技术和设备与发达国家的还存在一定差距，多色套印系统的准确度、印刷设备的稳定性等有待提高。因而研制一种适用于国产凹版印刷机的高精度自动套印系统，是提高我国凹印技术的关健。

基于传统PID控制器的套准系统已不能满足高速高精的生产要求[3]。为此，国内许多专家学者开展了众多相关的研究。李坤全等[4]针对凹版印刷机放卷系统设计了一个模糊自抗扰控制器，有效提高了系统控制的稳定性和抗干扰性。Chen Z. H.等[5]设计了基于模型的前馈比例微分控制器，有效减少了由张力波动引起的套准误差。Zhang E. P.等[6]提出了一种基于神经网络的主动扰动抑制控制策略，并将其应用于凹版印刷机的套印校正系统中。刘小刚等[7]针对凹版印刷机的无轴传动多轴同步控制系统，提出了模糊分数阶PID控制方法，极大改善了系统稳定性。刘成等[8]设计了二阶自抗扰控制器，实现了印刷色组单元的高精度控制。Huang G.等[9]提出了一种基于等价输入干扰的未知外部干扰抑制方法，有效提高了系统对时变外部干扰的鲁棒性。陈银环[10]设计了一种相邻交叉耦合控制策略，有效补偿了凹版印刷机滚轴的跟踪误差及多轴之间的同步误差。

尽管上述方法在提高凹版印刷机的套印精度方面取得了很好的效果，但它们的控制精度严重依赖于被控对象的精确数学模型。滑模变结构控制方法对系统参数摄动、外界扰动及数学模型不准确具有很好的鲁棒性[11-12]。基于此，本课题组拟以自动套印系统中交流永磁同步伺服电机（permanent magnet synchronous motor，PMSM）为被控对象，采用基于比例切换控制策略的滑模变结构控制方法，并对其仿真结果进行分析比较，以期为自动套印系统设计提供参考。

1 系统模型

套印准确是印刷的最基本要求，但由于各种因素的影响，套印不可避免地存在一定的偏差。PMSM以其体积小、功率因数高、响应快速及维护容易等优势广泛应用于包装印刷机械中[13]。因此，本课题组采用永磁同步电机驱动伺服系统调整定位技术来修正套印误差。其工作原理为：每个印刷单元配一台永磁同步伺服电机，先检测套印误差，再根据控制算法计算驱动电机的修正值，并调整修正辊的移动以补偿套印误差。

两相静止αβ坐标系下PMSM的数学模型[14]可描述为：

式中：iα、iβ分别为α、β轴定子电流；uα、uβ分别为α、β轴定子电压；Lα、Lβ分别为α、β轴定子电感；Rs为定子电阻；ψr为永磁体磁链；ω为转子转速；θ为电机转子位置。

定子电感为

式中Ld、Lq分别为d、q轴定子电感。

电磁转矩（Te）为

式中：iq为q轴定子电流；np为极对数。

机械方程为

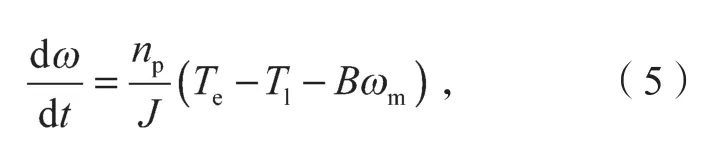
式中：Tl为永磁同步电机的负载转矩；J为转动惯量；B为转矩阻尼系数；ωm为转子机械角速度；Bωm为阻尼转矩。

由于三相交流永磁同步伺服电机具有较强的耦合性和严重的非线性，且某些电气参数具有可变性，因此该伺服系统的模型较为复杂。本课题组选取位置伺服系统的近似传递函数[15]，即

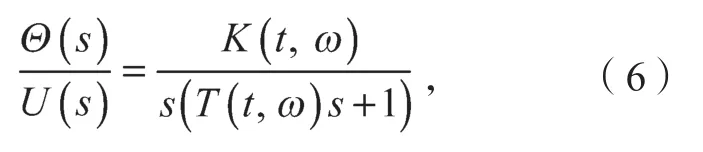
式中：Θ(s)、U(s)分别为位置θ和定子电压u的拉普拉斯变换；K为位置伺服单元系数；T为速度伺服单元时间常数。

2 滑模控制器设计

对交流传动等快速变化的非线性复杂系统，专家学者已经提出了各种控制方案。这些控制方案虽然解决了一些问题，但新的矛盾也涌现出来。有些方案因算法太复杂、稳定性及收敛性难以证明而不能实用。因此对快速变化的复杂工业系统，研究一种工程实用的有效控制方法是急待解决的问题[4]。

滑模变结构控制方法响应快，对系统参数和外部干扰呈不变性，这保证了系统是渐近稳定的。尤其可贵的是其算法简单，易于工程实现[16]。因此，采用滑模变结构控制方法设计伺服系统的位置控制器。其中，电动机的转角θ是控制对象的输出量，定子电压u是其输入量，参数K、Ts+1可以通过系统仿真实验测得。为构建一个简单而有效的滑模变结构控制系统，本课题组采用比例切换控制策略。

采用比例切换控制策略后，式（6）可表示为

式中：a1=0；a2=1/T；b=K/T。设b=133，a2=25，可得电机参数T=0.04 s，K=5.32。

输入量u为

对于位置伺服系统[17]，

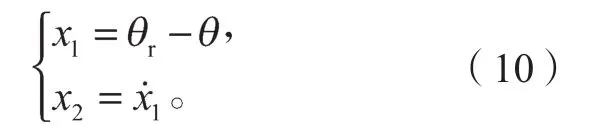
式（9）～（10）中：α′、β′为待求解的控制增益；θr为给定的角位移；θ为实际的角位移。

根据广义滑模条件

式（10）表示在有限时间内滑模面外的任意点必可到达滑模面。

反馈控制系统要求系统在进入滑动模态区后的运动必须是渐进稳定的，因此需确定恰当的切换函数s，使得其满足：

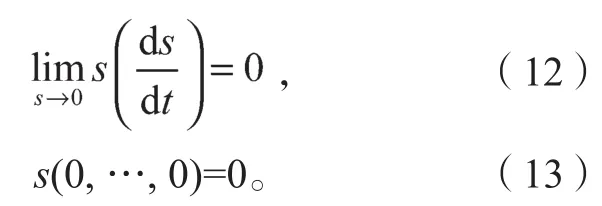
滑模面为

可得：

取c1=30，可得α′=500，β′=10。

3 系统仿真结果与分析

3.1 被控对象为时不变系统

在本设计中，系统的鲁棒性可以通过比较被控对象即电机参数（T,K）改变前后的响应特征曲线进行衡量。若系统具有强鲁棒性，则在电机参数发生变化后仍然具有很好的动态、静态性能。实验时，输入采用单位阶跃响应。

1）T值不变，改变K值

图1为参数K值变化时（K值减少20%和增加20%）的系统响应曲线。图中，曲线1为参数K变化前的响应曲线，曲线2为参数K变化后的响应曲线。

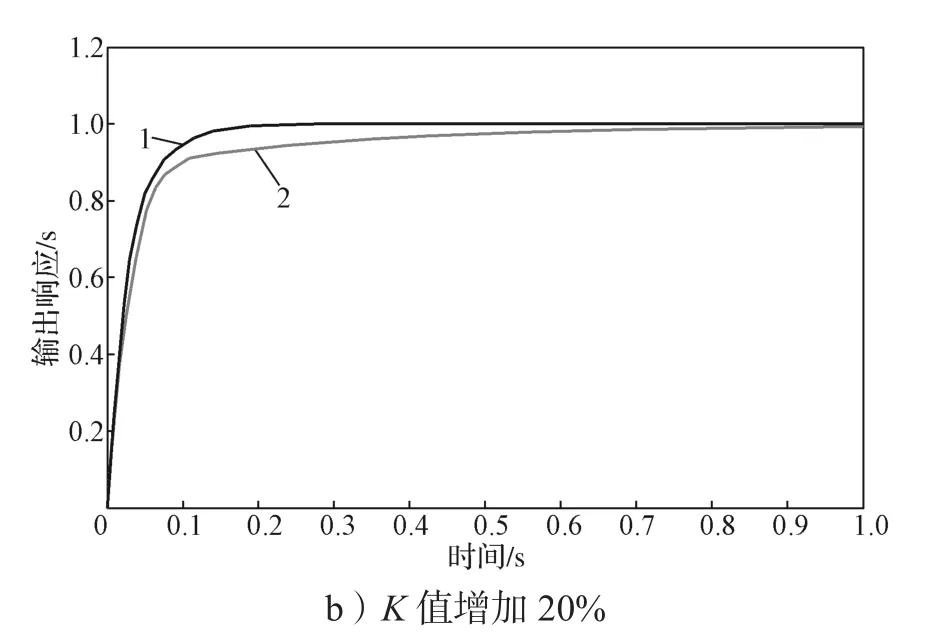
图1 K值变化时系统响应曲线Fig. 1 System response curve with changes in K

由图1可知，当T值不变时，K取值越小，系统的响应越快，且与输出给定值的误差越小。

2）K值不变，改变T值

图2为参数T值变化时（T值减少20%和增加20%）的系统响应曲线。图中，曲线1为参数变化前的响应曲线，曲线2为参数变化后的响应曲线。

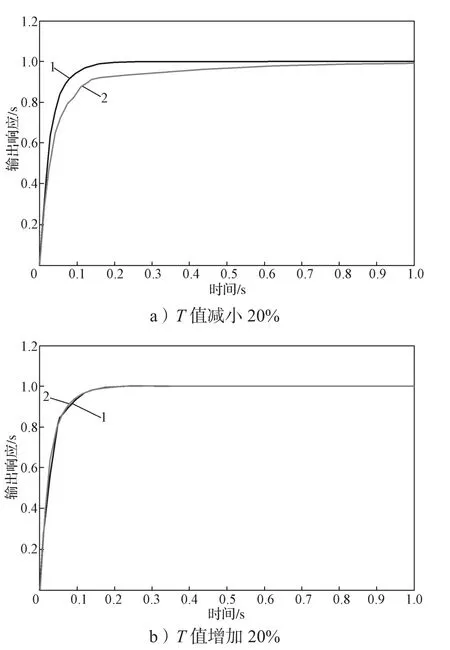
图2 T值变化时系统响应曲线Fig. 2 System response curve with changes in T

由图2可知，当K值不变，T值越大，系统的控制性能越好，响应越快，且与输出给定的误差越小，但T值不能太大，太大会出现超调现象。

通过上述改变T、K的仿真结果可得：基于比例切换控制策略的滑模变结构控制方法能够较好地克服永磁同步伺服电机参数变化带来的影响，系统具有较好的鲁棒性和跟踪精度。

3.2 被控对象为时变系统

交流伺服系统中永磁同步电机具有强耦合和严重的非线性，且部分电气参数可变。也就是说，除对上述时不变系统的参数进行讨论分析外，还有必要研究时变系统的输出情况。

设电机参数如下：

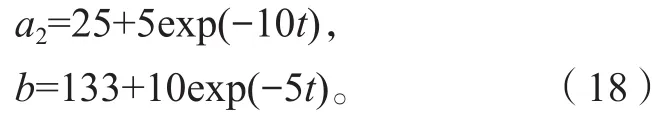
输入分别为方波信号和正弦波信号时，系统的响应情况如图3所示。

图3 不同信号作用下系统的响应曲线Fig. 3 System response curve under different signals

由图3可知，当被控对象参数按非线性变化时，基于比例切换滑模变结构控制方法的永磁同步电机伺服系统仍然有着很好的动态跟随性能。

3.3 两种控制方式的比较

当控制器分别采用PI控制器和滑模变结构控制器时，本课题组对其系统性能进行对比分析。为使两种控制方式具有可比性，将被控对象校正成典型II型系统。按闭环幅频特性峰值Mr最小准则，取频宽h=5，以确定PI控制器参数。设计PI控制器时，比例系数Kp越大，系统超调量变大，但系统响应速度加快，可以获得尽可能小的稳态误差；积分系数Ki越大，积分作用越弱，系统超调量变小，但系统响应速度变慢。综合考虑超调量不会过大的情况下，系统能有相对较高的系统响应速度，选择控制器增益：Kp=19.94，Ki=1。

图4为两种控制方式下系统的阶跃响应曲线。

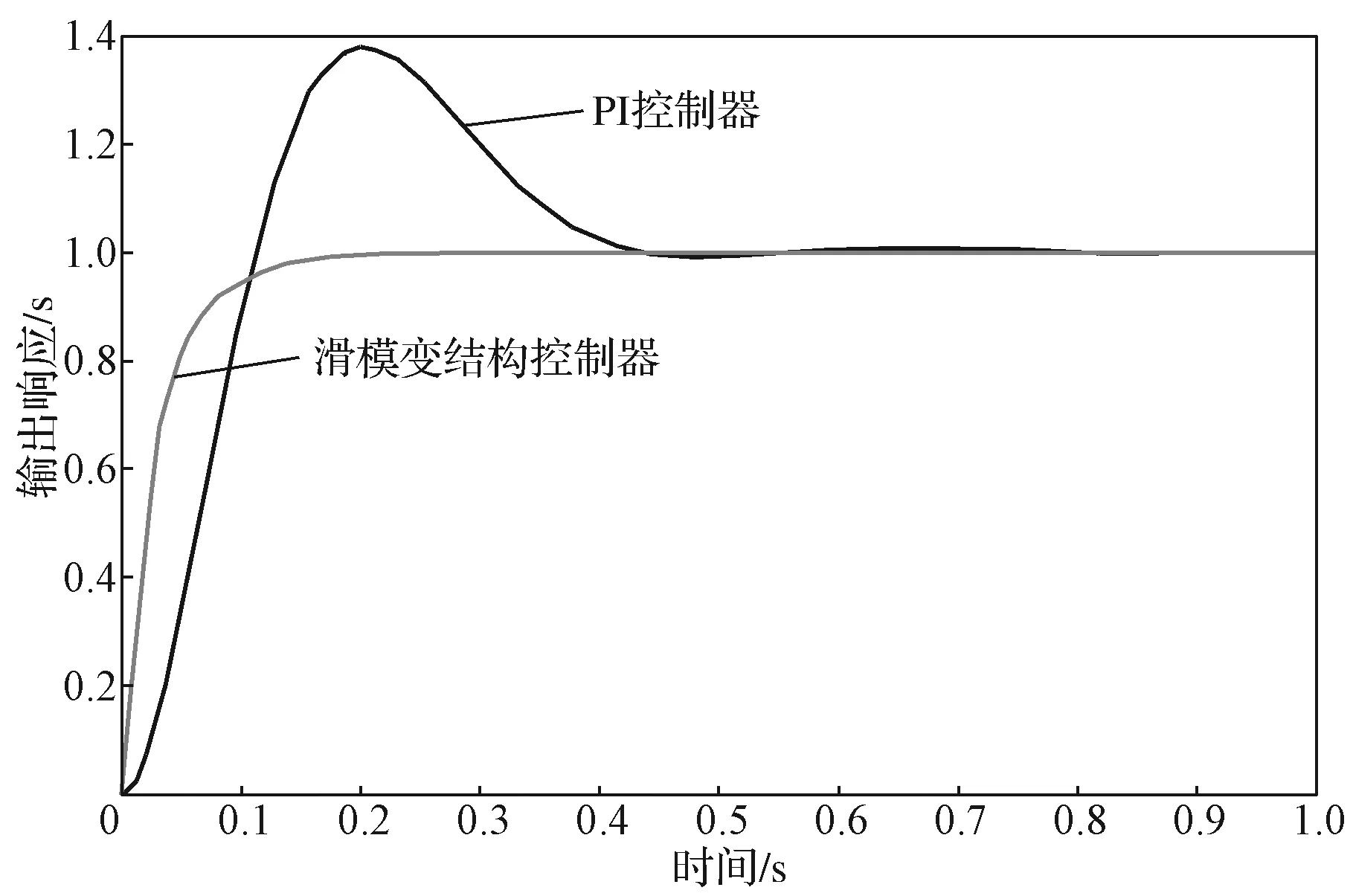
图4 系统阶跃响应曲线Fig. 4 System step response

由图4可知，采用PI控制器的系统响应在0.9 s后达到给定值，而采用滑模变结构控制器的系统响应在0.2 s后就达到给定值。可见，采用滑模变结构控制器的系统达到稳态的时间明显小于采用PI控制器的（两者相差0.7 s），且采用PI控制器的系统有较明显的超调现象。

图5为两种控制方式下系统的扰动响应曲线。

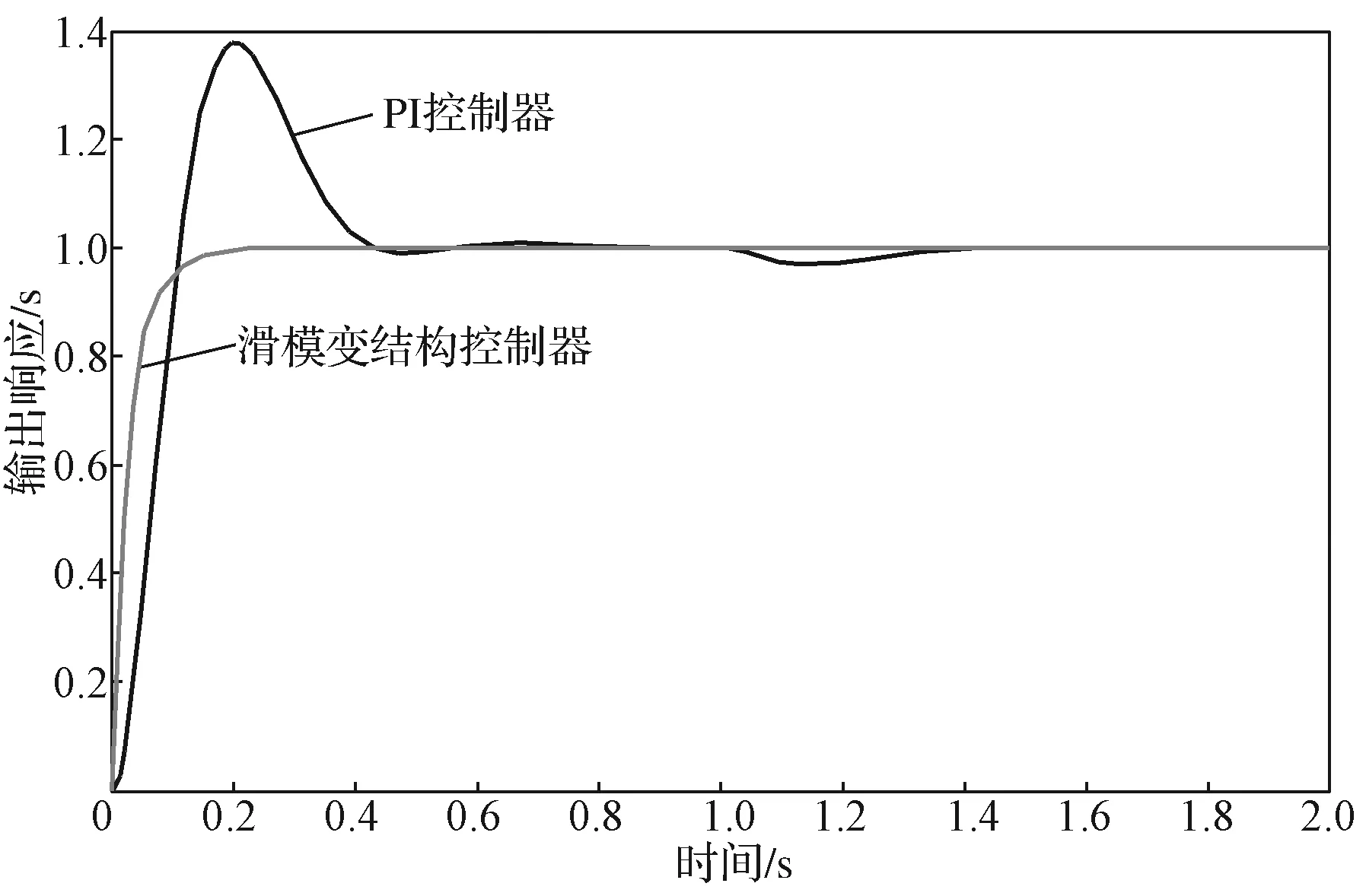
图5 系统扰动响应曲线Fig. 5 System disturbance response

由图5可知，在1 s时加入扰动，采用PI控制器的系统响应有较明显的波动，且需要较长一段时间（约0.4 s）才能重新达到原来的稳定值；而采用滑模变结构控制的系统响应曲线未出现波动，在扰动下依然能够很好地稳定跟踪给定值。

4 结语

本课题组以凹版印刷机套印系统中交流伺服系统为控制对象，为确保系统运行时的速度稳定性、电流快速性和位置准确性，设计了基于比例切换控制策略的滑模变结构控制方法。着重讨论了被控对象为时不变和时变时系统的响应情况，并对PI控制和滑模变结构控制两种控制方式下系统的响应、过渡时间、超调、抗干扰能力等进行了仿真分析。理论分析与仿真结果表明，所设计方法能对具有数学模型不精确、非线性、强耦合的被控对象进行控制，极大提高了伺服控制系统的性能。