回归学习本质，让深度学习真正发生

杜巧云

摘要：新课改走过了20年，以学生学习为中心的课堂改始终是教学研究的关键课题。在初中数学教学中就深度学习进行研究，有助于数学课堂教学质量的提升，有助于促进学生数学学科素养的发展，有助于促进教师专业发展。作为深度学习的设计师，只有基于数学课程内容领域的整体理解，基于学生体验高阶构架，才能促进深度学习的发生。本文将探讨了初中数学深度学习的促进策略，旨在让初中数学回归学习本质，让深度学习在课堂真正发生。

关键词：初中数学;深度学习;促进策略

中图分类号：A 文献标识码：A 文章编号：（2021）-39-349

初中数学深度学习是在教师引领下，学生基于理解，围绕特定的学习主题，调动思维，积极参与，对知识的活化和迁移，获得发展的有意义的数学学习过程。其目的是形成能力和素养，不同于知识的传递和识记的浅层学习。教师是深度学习躬行实践的最好答卷人，深度学习不仅需要躬行实践，更需要创造。如何让学习回归本质，让深度学习真正发生，笔者从创造深度学习情境，设定富于挑战性的问题，基于学生发散思考三个方面，作了以学习为中心设计深度学习的初步探索。

一、创造深度学习情境

教育家杜威说“教之于学，犹如卖之于买。别人没有买你的东西，就不能说你卖了”。数学知识是以情境为载体的，良好的学习情境才能调动学生参与学习的主动性。教师应该以教材内容为依据制定合适的生动的学习情境，为学生“学习”而设计，学生才乐于进入探索之旅。我们以《一次函数的图象和性质》这一课时的教学为例，教师可以充分利用多媒体技术将抽象知识直观动态呈现给学生们，设置生动化的学习情境完成教学。一次函数的图象是一条直线，但平移和增减性学生普遍有思维障碍。在教学中我引入desmot几何图形计算器，让学生在desmot几何图形计算器的情境探究一次函数性质。直观感知抽象难理解的K、b取值对图象平移和函数增减性质的影响，对图象平移的影响，K的取值对函数值增减性的影响，b的取值对图象与y轴交点位置的影响，在动态演示體验变化中，克服思维障碍。通过创建生动的学习情境开展教学，可以帮助学生更好地将知识与已有经验相结合，更好地掌握知识。

二、设定高品质的问题

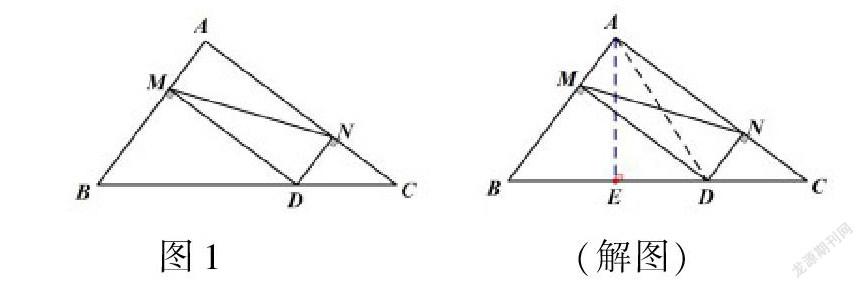
设定高品质的富于挑战性的问题，巧设问题串，以问题驱动整个过程，让学生感知体验，形成了探究性、启发式课堂。设定综合性的学习内容，学生乐于思考，给思维做体操，给予思维成长的台阶，让学生思维拾级而上，进阶高品质的思维，实施深度学习。在《矩形的定义与性质》的复习课中，设计了这样一道综合题。如图1，在Rt△ABC中，AB=6，BC=10，且∠A=90°，点D是斜边BC上的一个动点，过点D分别作DN⊥AC于N，DM⊥AB与M，连接NM，MN的最小值是多少。

本题综合考查矩形的对角线相等、勾股定理和垂线段最短。根据勾股定理，由AB、BC可求出AC;再根据矩形性质，将未知线段MN转化为求AD;再根据垂线段最短，将AD转化为垂线段AE;根据等积法求解AE，即MN的最小值。

三、基于学生发散思考，落实核心素养

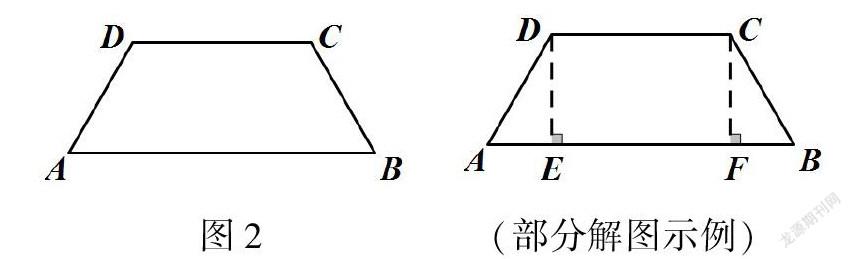
数学课堂是思维的课堂，不是教师的舞台，既做到面向全体，又照顾到学生之间差异。解题思路更不是教师思维的机械重复，要突破固化的思维模式，培养学生的发散思维。学生是课堂的中心，如何以学促教，是绕不开的主题。课堂上只有学生独立探索解决问题的办法，尝试多角度思考，发现不同的解决路径，才能给学生的核心素养形成搭建脚手架。以解题教学为例。在教学《平行四边形性质与判定的综合应用》时，教材第50页第9题，呈现如下：如图2 在梯形ABCD中AB∥CD，已知∠A=∠B，求证，AD=BC。学生经过读题理解题意、将条件与结论相靠拢、基于充分的思考探索，疏通已知和未知的关联。个人猜想经过小组合作交流验证，小组班内展示，分享了以下四种解法。

方法一延长AD、BC利用等腰三角形求解;方法二在梯形内部构造辅助线，作DE⊥AB于E，CF⊥AB于F利用全等求解;方法三作CE∥AD交AB于E，利用平行四边形求解;方法四作BE∥AD，交CD的延长线于E，利用平行四边形性质求解。基于充分思考，组内互助异组分享，超越自己原有的认知能力。发散思考，从核心内容和知识团或知识链整体入手，以课本习题承载等腰三角形、全等三角形、平行四边形等相关知识。在几何教学中，学生通过发散思考，发展数学抽象、几何直观、逻辑推理的关键能力和核心素养，让思维在课堂这个教学主阵地生根发芽，呈现精彩的课堂。

让学习回归学习本质，让深度学习真正发生，这是新时代赋予教师的时代使命。研究课堂，创新课堂，关注核心素养的落地。促进本土化的实践探索，深耕课堂，我们一直在路上。

参考文献

[1] 刘晓玫.《深度学习走向核心素养》[M]. 教育科学出版社，2019年11月：140.

[2]林忠玲《策动深度学习的整体性变革》[N] 《中国教师报》2021年3月10号（836期）