柯西变异的骆驼算法优化与应用

任春慧，刘 升，张伟康，张微微

上海工程技术大学 管理学院，上海201620

生活已成为开发许多优化算法的启示源，这些优化算法可分为确定性算法和随机算法[1]。确定性算法是具有可预测行为的算法，如果给定特定输入，它们将始终产生相同的输出。随机算法可以分为启发式算法和元启发式算法，它们之间的差别很小。启发式算法在可接受的时间内解决问题，但不能保证可以找到最佳解决方案，这意味着没有这样的最优性。虽然元启发式算法意味着“超越”或“更高层次”，但它们通常比简单启发式方法表现更好。另外，所有元启发式算法都使用了随机化和局部搜索之间的某种权衡。

在过去的几十年中，元启发式算法吸引了越来越多研究学者的关注，现在仍然是一个活跃领域。后来提出了几种算法，例如粒子群算法[2]、蚁群优化算法[3]、细菌觅食优化算法[4]、花授粉算法[5]、磷虾群算法[6]、乌鸦搜索算法[7]等。如今，有许多实际的优化问题需要解决，任务是针对大多数的问题而不是所有问题设计更好的算法。

Ibrahim和Ali在2016年提出的骆驼算法[8]是一种元启发式优化技术，它模仿了骆驼在沙漠中觅食过程中的行进行为，可以描述为它们向着食物源位置的合作运动，接收、感知和分析空气中的气味以确定食物源或配对伴侣的潜在方向。由于有多循环嵌套和多个参数选择，该算法具有复杂的结构，这会对执行效率和内存大小产生负面影响。本文介绍改进的骆驼行进行为算法（MCA），显著提高了其计算速度和收敛性，同时简化了算法结构。为了检验其性能，进行仿真研究，将改进的算法与CA、PSO和CSA算法进行了比较，并在工程应用中进行测试抗干扰智能天线优化，结果表明MCA能有效处理实际工程问题。

1 骆驼优化算法

1.1 骆驼行进行为

骆驼可以在高温和缺水的情况下，适应长时间的生存。在夏季，它平均8~10天涉水一次，并通过脱水减去多达30%的重量。具体而言，当平均温度约为30℃~35℃时，骆驼在没有水的情况下可以生存10~15天，但当温度高于46℃时，则需要较短时间的饮水。

在骆驼穿越沙漠到达某个目的地的过程中，它们遵循有组织的先天性行为来寻找食物。骆驼散布在某个地区，寻找食物，一旦某个骆驼到达一个绿洲，它就会与骆驼群其他成员进行某种信号交流，指引其他骆驼来到绿洲处。只要骆驼群中任意个体能看到信号源骆驼的位置，它们就可以改变方向，寻找通往绿洲的道路。由于沙漠中沙丘的存在，并非所有骆驼都可以看到食物供应的地点，未看到的骆驼继续随机运动寻找下一个绿洲。在此行进期间，另一头骆驼可能会找到更好的食物供应位置，因此它会与其他骆驼再次进行信号交流，更改它们前往该新位置的路线，这个过程一直持续到骆驼到达一定的绿洲为止。

从上述系统行为中，启发了骆驼算法。骆驼行为[9]的概述可以归纳为以下几点：

（1）骆驼以集群的形式行进。

（2）骆驼散开去寻找绿洲。

（3）到达区域的骆驼与其他骆驼进行信号交流，来指引前进方向。

（4）沙丘可能会阻止某些骆驼看到绿洲区域，这些骆驼会继续随机运动。

（5）在此行进过程中，另一只骆驼可能到达更好的绿洲，然后重复更新过程。

值得一提的是，骆驼群在过去的整个行进过程中会一直寻找最佳位置。换句话说，骆驼群是根据全局最佳位置而不是局部最佳位置来更新其行进路径。

1.2 骆驼优化算法

假设有N只骆驼穿越D维环境。骆驼i在时间迭代(iter)时的位置可以表示：

其中，i=1,2,…,N；iter=1,2,…,itermax。

开始时(iter=0)，骆驼在沙漠中散布开来，随机寻找绿洲，如下式所示：

其中，d=1,2,…,D；Rand表示一个均匀分布在0和1之间的随机数；xmin表示骆驼位置的最小限制（优化变量），xmax骆驼位置的最大限制（优化变量）。

因此，每个骆驼的位置都要经过一定的适应度来确定最佳位置。环境温度直接影响骆驼的行进，并显著影响骆驼的耐力E。由于不同的骆驼向稀疏位置移动，它们遇到的温度不同，导致每个骆驼的耐力水平也不同。骆驼i在迭代时间iter时的温度T是最小温度范围Tmin和最大温度Tmax之间的波动如下：

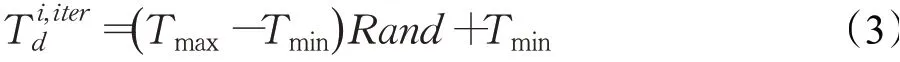
温度对骆驼耐力E的影响：

从等式（4）可以清楚地看出，骆驼的承受力与温度成反比，且耐力越高，骆驼步距越宽。

沙丘可能会挡住某些骆驼的视线，使它们无法更新通往某只骆驼发现绿洲的路线。因此，有两种方案可以更新每个骆驼的位置。

当骆驼的能见度v大于特定的能见度阈值时，更新函数如下式：

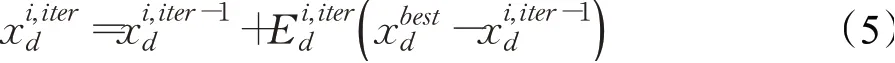
当骆驼的能见度v小于能见度阈值时，会发生更新过程的第二种情况，在此情况下，骆驼会根据等式（2）随机更新其位置。新位置也会根据指定的适应度函数的影响，确定当前的最佳位置。如果当前位置优于过去的位置，则新的位置是全局最佳位置，否则过去的位置仍然是全局最佳位置。应该注意的重要一点是，骆驼能见度在每次迭代中都是0到1之间的随机数，因为它取决于沙丘存在的随机位置。更新过程一直持续到达到最大迭代次数或达到适应度函数中的某个阈值为止。

骆驼算法[10]如下所示：

输入：目标函数f(x)，骆驼位置限制xmin和xmax，设置温度范围Tmin和Tmax，设置骆驼群的规模N，设置可见性阈值v，最大迭代次数Maxiter

1.初始化：根据等式（2）初始化每个骆驼的位置，对位置进行适应度调整；确定当前的最佳位置；为每个骆驼随机分配能见度v。

2 骆驼优化算法的改进

2.1 柯西变异策略

柯西分布是概率论中常见的连续型分布之一，其密度函数表达式可定义为：

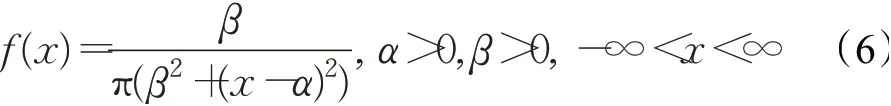
表示为C(α,β)，其中α和β是两个参数。特别地，当α=1，β=0时，可得标准的柯西分布的密度函数：

高斯分布和柯西分布的比较如图1所示，从图中可以看出柯西分布图形是对称的且两翼较为平坦、宽大，在原点附近有一个较低的极值，且水平下降比高斯分布下降慢，柯西分布在水平方向上越接近水平轴，变得越缓慢，因此柯西分布可以看作是无限的，因此，从概率上讲，Cauchy分布具有更宽的分布范围，它允许较大的变异，因此采用柯西变异产生的子代距离父代较远的概率高于高斯变异，从而易于跳出局部最小点。以这种方式可以产生更多样化的个体和涵盖更多的主要空间。与此相反，高斯变异能够以其最接近的空间完成准确邻近的探索[11]。

图1 柯西（Cauchy）分布和高斯（Gaussian）分布比较Fig.1 Comparison of Cauchy distribution and Gaussian distribution

针对骆驼算法易陷入局部最优的特点，利用柯西变异来增加目标的多样性，提高算法的全局搜索能力，增加搜索空间。

由于柯西分布函数的峰值较低，该特点能够缩短变异后的骆驼个体在邻域周围搜索的时间。因此在求得当前最优解后，使用公式（7）所示的更新公式对当前全局最优解进行变异处理。

2.2 改进的骆驼算法

柯西分布函数从峰值向两侧下降相对平缓，骆驼个体受局部的极值点约束力在进行柯西变异后下降，并且柯西分布函数的峰值相对较小，骆驼个体在变异后会使用相对较少的时间来搜索相邻区间，把更多的时间放在搜寻全局最优值上，使得改进的骆驼算法在寻找全局的最优值方面具备很好的调节能力。用柯西变异进行随机扰动有利于增加种群的多样性从而避免算法陷入局部最优，提高全局搜索最优值的能力。柯西分布的特征使其能够产生与原点相距较远的随机数，这意味着经过柯西变异后的骆驼个体具备了能够迅速逃离局部极值的能力。

通过融合柯西变异函数对骆驼行进分布进行优化处理后，使得CA算法具有更好的局部寻优能力，改进后的CA算法流程图如图2所示。

图2 改进后的算法流程图Fig.2 Improved algorithm flow chart

3 函数测试与结果分析

3.1 仿真实验环境

本仿真测试环境为操作系统Windows10，CPU为Intel®Core™i5-5200U，主频2.7 GHz，内存为8 GB，仿真软件为Matlab2019a。

3.2 测试函数

为了验证MCA算法的性能，选择三个单峰和三个多峰基准函数进行仿真测试实验。表1列出了选定的六个基准测试函数，F1(x)到F3(x)为单峰基准函数，F4(x)到F6(x)为多峰基准函数，这些基准测试函数的最小值等于零。

表1 基准测试函数Table 1 Benchmark function

3.3 实验的初始参数设置

本文将MCA与原始CA，乌鸦搜索算法（CSA）和粒子群优化算法（PSO）进行比较[12]。在以下条件下测试算法：初始种群规模N统一设为50，最大迭代次数为500次。对于MCA和CA，可见性阈值v=0.1，位置限制xmin=-32,xmax=32，温度范围Tmin=30℃和Tmax=60℃；对于CSA：飞行长度fl=2，感知概率AP=0.1；对于PSO：惯性系数w=0.9,wdamp=0.4，学习因子c1=1.5,c2=2。

3.4 实验结果与分析

与原始CA相比，MCA的主要优势在于其执行速度高，内存小，大幅度减少了运行的时间，提高了执行效率。MCA仅需要一个骆驼的全局最佳位置向量，该骆驼是[1×Dim]矩阵。除了显著减少内存大小外，该算法还减少了一个循环，与CSA相比，MCA的执行速度得到了提高。

为了验证MCA在执行速度方面优于CA、CSA和PSO，对算法运行时间进行了测量。表2列出了针对30次运行和单次运行的每个测试函数执行每种算法所需的时间。图3显示了30次运行的执行时间，图4显示了单次运行的平均时间。从表2以及图3和图4中可以看出，MCA比CSA、CA和PSO运行速度更快。因此，MCA非常适合在线优化系统，该系统需要较小的内存大小并快速响应其参数的突然变化。

图4 单次运行的执行时间Fig.4 Execution time of single run

表2 测试函数实验运行时间Table 2 Test function experiment running time

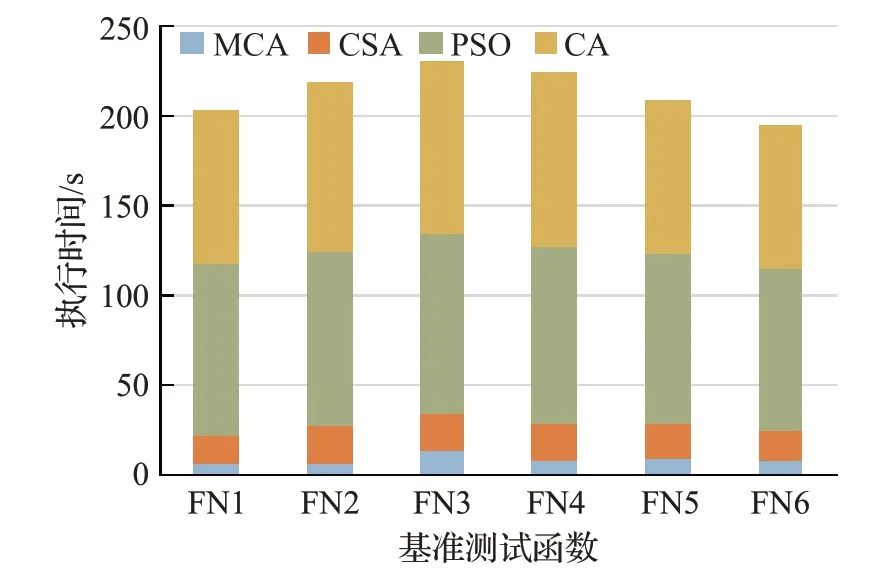
图3 30次运行的执行时间Fig.3 Execution time of 30 runs

从精度至关重要的离线优化的角度出发，对每个测试函数进行30次运行，获得平均值、标准偏差和测试函数最佳值的中值。还根据以下公式计算每种算法的成功率（SR）：

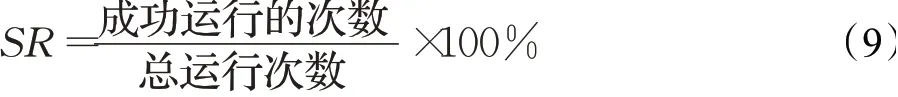
其中成功运行次数表示达到以下条件的运行次数：

表3 展示了MCA、CSA、PSO、CA这四种算法独立运行30次后所得到的最优值、均值、标准差、中位数和成功率的结果。

根据表3，可以清楚地看出对于所选测试函数，MCA的寻优能力最强明显优于CSA、PSO和CA。对于函数F1、F5、F6，MCA可以直接搜索到最优值0，寻优效果可以达到100%；对于函数F2、F3、F4，MCA寻优效果良好，且接近PSO，具有PSO相当的性能，且对于多峰函数MCA表现出比PSO更好的成功率。

表3 测试函数实验结果Table 3 Experimental results of test function

为了直观地展示MCA的寻优性能，作出了关于测试函数的迭代收敛曲线图，如图5所示。

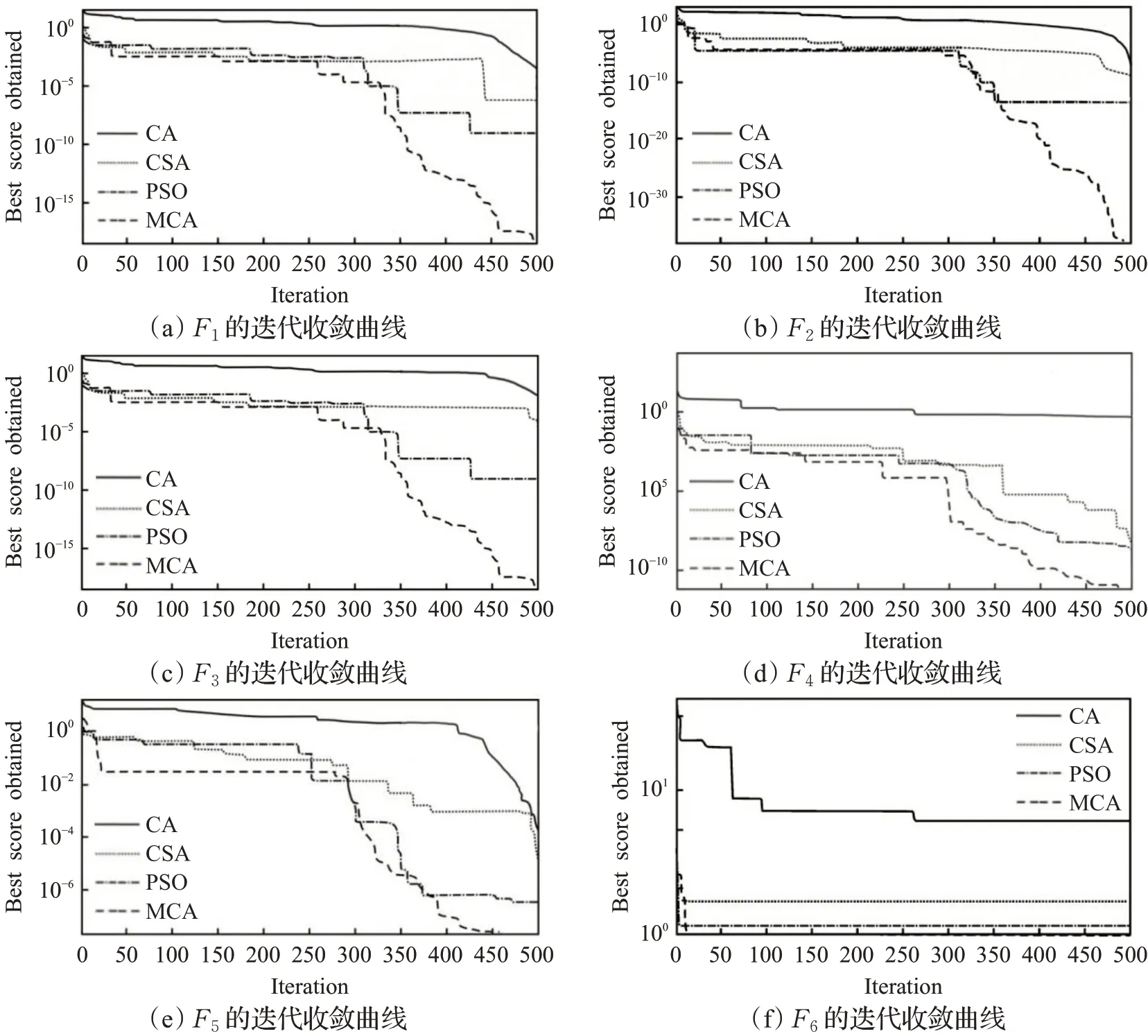
图5 测试函数收敛曲线图Fig.5 Convergence curve of the test function

3.5 高维系统中的性能比较

没有一种算法可以精确有效地执行所有优化问题，因此，MCA的缺点出现在高维优化系统中。对于高维（维度d=200），与多模式优化系统的PSO相比，MCA性能下降，CSA的失效性最为明显，如表4所示。从实验结果来看，MCA在高维函数求解中仍具有较好的寻优稳定性。对于多峰函数，四种算法执行效果都不好，函数会形成大量局部极值区域，易陷入局部最优且不易跳出，在高维测试函数下求解难度较大，在测试函数维数大于200维时，就属于大规模函数优化问题。随着搜索空间维数的增加，问题的复杂度以及指数级数的增长，从而出现“维数灾难”问题，根据无万能算法理论，没有任何一个算法适合解决所有问题，所以这个结果是可以接受的。尽管局部最佳使算法复杂化并减慢了速度，但仍显著提高了算法的精度。针对此点，可以得出MCA在低维离线优化和高维单峰离线优化过程中是有效的。

表4 MCA高维函数求解结果Table 4 Solution result of MCA high dimensional function

4 工程优化应用

4.1 抗干扰智能天线系统

抗干扰智能天线[13]可用于军事，这是一个实时系统，它经常不断地更新其操作参数。图6说明了M元素智能天线系统的工作原理和参数。所需的传输与接收站固定在站点（LOS）线内。其他干扰源沿不同方向分布，以传输伪造消息或仅向标记功能干扰原始系统。抗干扰智能天线系统尝试将天线主波束[14]定向到所需的传输方向，并在干扰信号的方向上定位零点。实际上，所需信号与干扰之间是否存在任何相关性信号，传统的波束形成算法无法完美消除干扰信号。在这种情况下，传统的波束形成算法只能衰减干扰信号。但是，有时会以高于所需信号功率的功率发送干扰信号，因此在这种情况下衰减将无效[15]。骆驼算法与信号之间的相关性无关，无论其传输功率大小如何，都可以完美消除干扰信号。

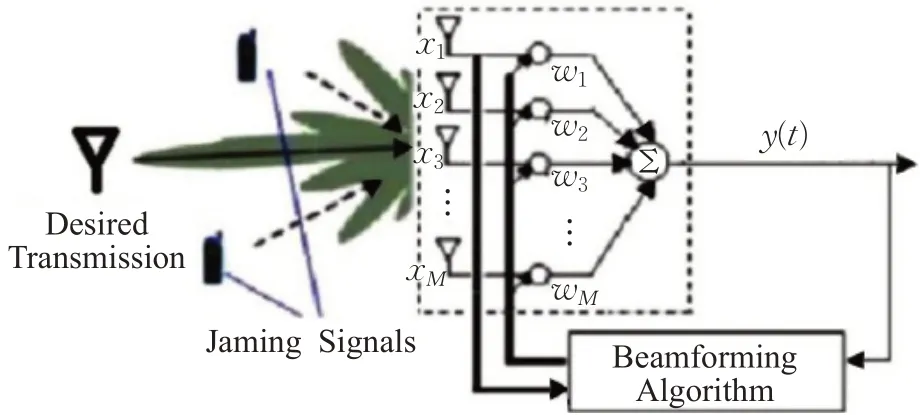
图6 M元智能天线系统Fig.6 M-dimensional smart antenna system

4.2 抗干扰智能天线优化

考虑到有(k+1)个信号从不同方向照亮M元素智能天线。这些信号由它们的强度S（信号功率的平方根）表示，使得{S0,S1,…,Sk}。假设接收信号S0是从宽边方向照亮智能天线的所需信号(Φ=90)。所有其他信号均被视为干扰信号。感应到的信号所有元素都可以用矢量符号表示，阵列系统的复数权重矢量表示为。智能天线系统的输出信号为：

其中，上标H表示复共轭转置。

由智能天线系统采集的接收信号矢量最初的构造为：

其中，ak是指到达角为Φk的第k个信号的导引向量。

转向矢量信号可以表示为：

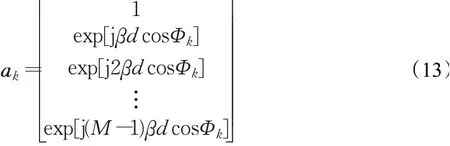
其中，d表示每两个相邻元素之间的波长(λ)，而β表示传播相位常数：

对于天线阵列[16]，只要天线元件是全向的，辐射方向图就等于阵列系数(AF)。因此，可以从阵列因子方程确定辐射方向图，如下所示：

其中，a(Φ)代表任意角度(Φ)的一般转向矢量：

权重向量元素之间的相位角(δ)决定了应朝向所需信号方向定向的天线主波束角Φ0。以下准则确定权重矢量

元素之间的相位角：

所需的信号角度为(Φ0=90°)，因此δ的值等于零。但是，权重向量的大小决定了天线阵列因子的零位。结果，权重向量的大小||w是此类系统的优化变量。对于上述系统，适应度函数F为：

数值示例：考虑M=10智能天线系统，其期望信号强度等于S0=1。假设存在一个极端干扰问题，包括三个强度分别为S1=3,S2=2,S3=3。

以下情况表示四个干扰信号的不同到达角度：

Case 1：Φ1=20,Φ2=60,Φ3=120

Case 2：Φ1=30,Φ2=80,Φ3=140

Case 3：Φ1=50,Φ2=100,Φ3=130

表5 为应用MCA后每种情况下的权重向量的优化大小。图7针对每种情况从权重向量得到的阵列因子的归一化幅度。显然，无论信号之间的相关性如何，天线系统都可以通过将零点指向其到达角度来完全消除干扰信号。

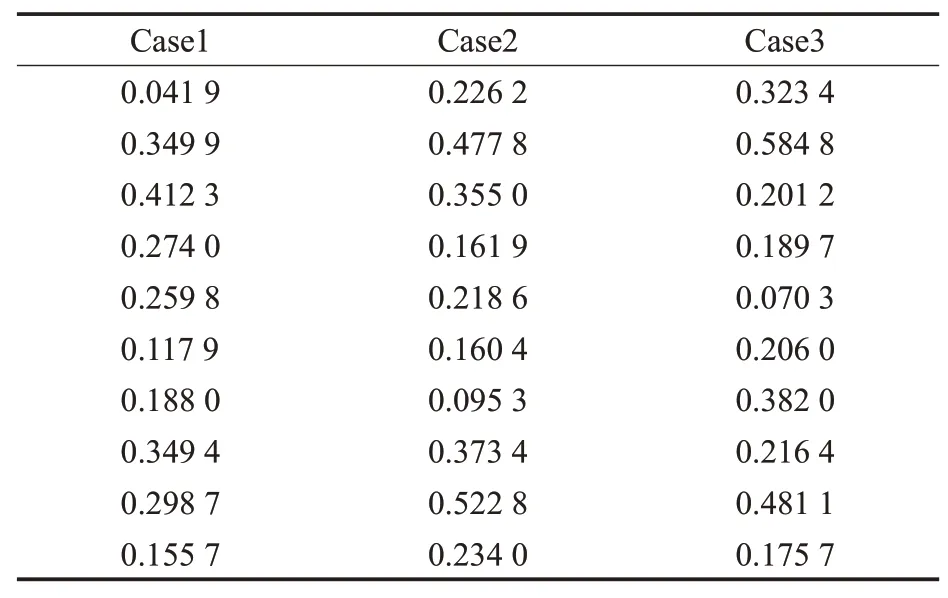
表5 智能权重向量优化幅度Table 5 Intelligent weight vector optimization amplitude

图7 优化的智能天线归一化阵列因子Fig.7 Optimized normalized array factor for smart antenna

5 结束语

本文提出了一种模仿骆驼行进行为的新型改进CA算法。在全局位置更新后的值引入柯西变异算子，增加了种群多样性，降低算法陷入局部最优的可能性。由于减少了原始算法中使用的设置参数的数量，因此该算法的结构很简单。使用具有不同变量维度的不同单峰和多峰基准函数测试了修改后的CA，结果表明，MCA具有更好的寻优能力和鲁棒性。且对于低维变量，修改后的CA的精度与PSO相当。通过优化受约束的工程应用，抗干扰智能天线的优化来验证MCA的性能。对于抗干扰智能天线，该算法通过将零点指向其方向来完美消除干扰信号。此外，进一步研究骆驼算法参数值可能会进一步提高其性能和收敛速度，将算法应用到更广泛的领域。