事件触发下多智能体系统固定时间二分一致性

李振涛，冯元珍，王正新

南京邮电大学 理学院，南京210023

近年来，多智能体系统因其在无人机编队控制[1-2]、环境监测[3]等多个领域的广泛应用吸引了众多学者的关注。一致性问题作为多智能体系统协同控制的基础，已经成为控制领域目前的研究热点之一。值得注意的是，现有文献主要针对多智能体系统的渐近一致性问题进行了研究。针对几类具有不同动力学的多智能体系统，文献[4-8]分别给出了时间趋于无穷时系统实现一致性的条件。但在工程应用中，这样的收敛时长并不能满足实际需求。与渐近一致性相比，有限时间一致性要求多智能体系统在有限时间内实现一致性，故其可满足实际应用对系统收敛时长有限性的要求。基于文献[9]提出的有限时间稳定性理论，文献[10]针对由离散时间子系统和连续时间子系统组成的切换多智能体系统，研究了其有限时间一致性问题。文献[11]解决了具有不匹配扰动和非线性动力学的高阶多智能体系统的有限时间一致性问题。然而，由于有限时间一致性中的收敛时间依赖于多智能体系统的初始状态，但系统的初始状态很多时候并不易于获取，由此导致有限时间一致性在工程应用中有一定缺陷。

为克服有限时间一致性的局限性，许多学者进行了固定时间一致性的研究工作。固定时间一致性的实现不仅要求多智能体系统在有限时间内实现一致性，还要求对任意初始状态，系统的收敛时间具有常值上界[12]。文献[13]研究了有向拓扑结构下带领导者的非线性多智能体系统的固定时间一致性；文献[14]研究了一般有向图下带领导者和不带领导者的一阶非线性多智能体系统的固定时间一致性；文献[15]研究了具有符号有向图的多智能体系统的有限时间二分一致性。然而，文献[13-15]提出的控制协议均为连续控制协议，这意味着在实现一致性过程中，智能体之间需要频繁地进行通信交流和控制更新，从而导致多智能体系统能源大量消耗。基于事件触发的控制策略可以有效解决这一问题。文献[16]基于事件触发机制，研究了在跟随者拓扑图为无向图时带领导者的一阶多智能体系统的固定时间一致性。文献[17]在文献[16]的基础上，研究了具有扰动的带领导者一阶多智能体系统的固定时间一致性问题。文献[18]研究了带领导者的一阶非线性多智能体系统基于事件触发机制的固定时间一致性问题。文献[19]在文献[16]和[17]的工作基础上，考虑了具有输入时滞的带领导者一阶多智能体系统的固定时间一致性。目前基于事件触发机制的固定时间一致性问题研究，主要针对带领导者的多智能体系统，通过引入跟踪误差将一致性问题转化为误差系统的稳定性问题；无领导者存在时的相关问题尚未深入开展。鉴此，本文研究了基于事件触发机制的一阶多智能体系统的固定时间二分一致性问题。本文的主要贡献体现在以下三个方面：首先，与文献[16-19]相比，本文将信息交流图从无向正图拓展到了符号有向图，且多智能体系统中无领导者存在；其次，在文献[15]工作的基础上，设计了一种基于事件触发机制的分布式控制协议，减少了能量损耗，并证明在所设计控制协议作用下一阶多智能体系统可有效避免Zeno现象的发生，使控制协议更具现实意义；最后，给出了一阶多智能体系统实现固定时间二分一致性的收敛时间常值上界表达式。

1 预备知识及问题描述

本章介绍本文要用到的图论基础知识[20]和相关引理，并简单描述将要讨论的问题。

1.1 图论基础知识

令G={V,E,A}表示由N个结点组成的符号有向加权图，其中V={v1,v2,…,vN}为点集合，E⊆V×V为边集合，A=[aij]∈RN×N代表加权邻接矩阵。当(vi,vj)∈E时aij≠0,否则aij=0。对于符号有向图G，有向边(vi,vj)∈E表示信息从结点vi流向结点vj。从vi1到viq的有向路径指的是由一系列有向边(vip,vip+1)∈E构成的边序列，其中p=1,2,…,q-1且该有向路径中的结点彼此不同。如果符号有向图G中的任意两个结点之间都存在有向路径，则称G是强连通的。如果有向图G的结点可以分为V1和V2两组且满足V1⋃V2=V,V1⋂V2=Φ,aij≥0(∀vi,vj∈Vq,q=1,2)和aij≤0(∀vi∈Vq,∀vj∈Vr,q=1,2;r=3-q),则称符号有向图G是结构平衡的；否则，G是结构不平衡的。符号有向图G的拉普拉斯矩阵定义为L=[lij]N×N,其中若符号有向图G中的所有权值均非负，则称G为正图，这是一类特殊的符号有向图。

1.2 相关引理

引理1[21]若符号有向图G是强连通的，则G是结构平衡的当且仅当下列两个条件中任意一条成立：

（1）存在矩阵D∈D使得DAD的所有元素均非负，其中D={diag{d1,d2,…,dN},di=±1}。

（2）G的拉普拉斯矩阵L有且仅有一个零特征值且L的秩为N-1。

引理2[15]若符号有向图G是强连通结构平衡的，则存在正向量η=[η1,η2,…,ηN]T和引理1中定义的对角矩阵D，使得ηTDL=01×N,其中L为符号有向图G的拉普拉斯矩阵。

引理3[15]若符号有向图G是强连通结构平衡的，则存在矩阵D∈D使得DLD为一个正图的拉普拉斯矩阵。定义向量集：

则有：

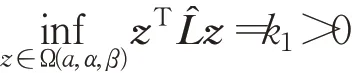
引理4[22]对于任意给定的xi>0(i=1,2,…,N)和s>μ≥1,下列不等式恒成立：

引理5[12]对于系统

如果存在一个连续正定的径向无界函数V(x(t))：R→R+⋃{0}且满足：

（1）V(x(t))=0⇔x(t)=0；

（2）系统的任意解x(t)满足：

其中，ᾶ>0,β͂>0,01,则系统（1）实现全局固定时间稳定且收敛时间T满足：

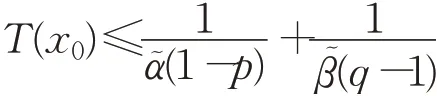
引理6[15]若符号有向图G是强连通结构不平衡的，则存在对角阵Ω=diag{ω1,ω2,…,ωN}>0使得ΩL+LTΩ>0。

1.3 问题描述

考虑由N个一阶智能体组成的多智能体系统，智能体i的动力学模型为：

其中，xi(t)∈Rm和ui(t)∈Rm分别表示第i个智能体的位置状态和控制输入。

注1为表述方便起见，不失一般性，本文仅在m=1时进行讨论，m>1时相关结论可利用克罗内克积的性质进行推广。

假设智能体间的信息交流图G满足以下条件：

注2文献[16-19]研究了具有正图的多智能体系统固定时间一致性问题。本文将信息交流图拓展到符号有向情形，考虑了智能体间的权重可为负值的情况，即智能体间除相互协作外，还存在博弈、竞争等关系，在工程应用中，更具有广泛性。

定义[15]对具有符号有向图的多智能体系统（2），若存在控制输入ui(t)，使得对任意初始状态xi(0)，都有：

且存在一个正常数Tmax,使得T≤Tmax恒成立，则称多智能体系统（2）实现固定时间二分一致性，其中T为依赖于初始状态的收敛时间。

2 主要结果

本章考虑具有符号有向图的一阶多智能体系统（2）的固定时间二分一致性问题。为有效减少控制过程中多智能体系统的能源损耗，设计如下基于事件触发的控制协议：

其中，控制增益a>0,b>0,控制参数0<α<1,β>1；s[a]定义为其中sign(⋅)为符号函数。定义，则在任意时间段为第j个智能体的最新触发时刻。

令

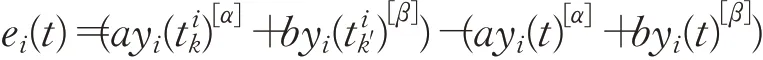
多智能体系统可以简写为：

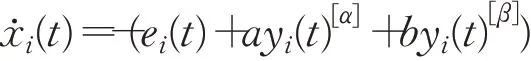
定理1若符号有向图G是强连通的，设计分布式触发函数φi(t)：

其中，c>0，当第i个智能体的触发函数φi(t)>0时，事件触发，此时该智能体的控制协议采集信息更新。

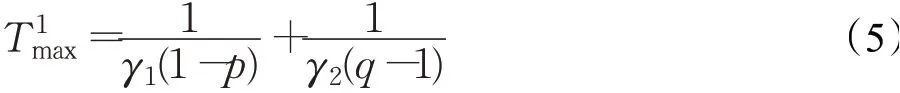
其中，λmax(LTH2L)为矩阵LTH2L的最大特征值，k1的定义见引理3及

ηi(i=1,2,…,N)的定义见引理2，ρ的定义见定理1证明过程。

否则，当G为结构不平衡图时，若

证明 考虑到符号有向图分为结构平衡图和结构不平衡图。接下来，将在这两种拓扑结构下分别证明多智能体系统（2）在控制协议（3）和触发函数（4）的作用下，均可实现固定时间二分一致性。

首先证明当G是结构平衡图时相关结论成立。构造Lyapunov函数：

其中，ηi的定义见引理2。

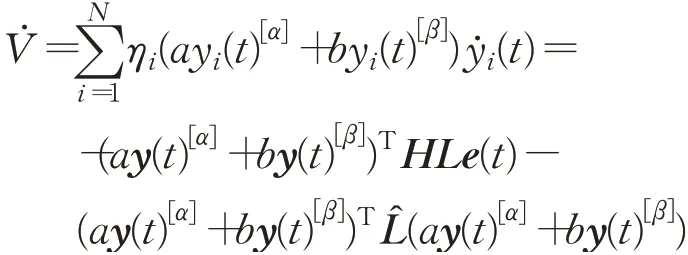
为方便证明，引入中间变量

由引理4可得：

和

联立式（10）~（12），可得：

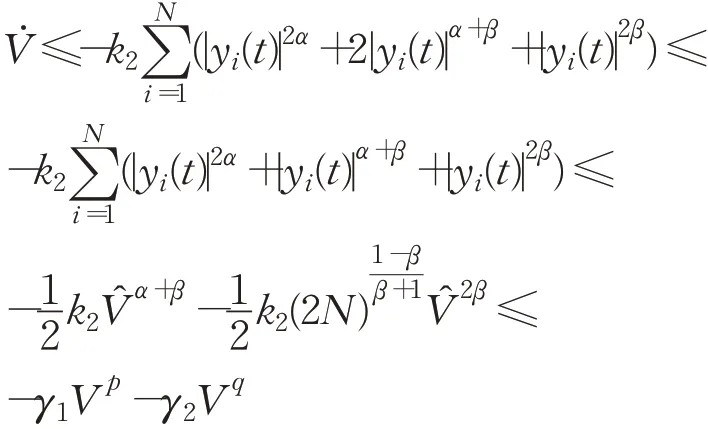
其中，γ1,γ2,p和q的定义见式（6）。由引理5可知，V在固定时间内收敛到0，即y(t)=Lx(t)=0。由引理1知，L的秩为N-1且有LD1N=0,故有x(t)∈span{D1N},即,其中收敛时间T的上界为

其次，当图G是结构不平衡图时，构造Lyapunov函数：

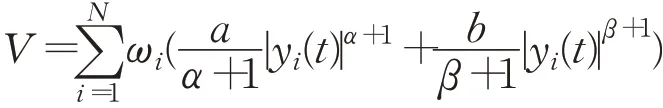
其中，ωi的定义见引理6。

综上所述，当假设1成立时，应用控制协议（3）和触发函数（4），多智能体系统（2）实现固定时间二分一致性。证毕。

注3由式（5）和（7）知，若控制增益a=b，当控制增益增加时，固定时间一致性收敛时间上界T1max和T2max相应减小。因此，在实际应用中，可选取相对较大的控制增益来提高系统收敛速度。

注4当控制增益a=0或b=0时，应用控制协议（3）和触发函数（4），多智能体系统（2）可以实现有限时间二分一致性。

注5当强连通图G为结构不平衡图时，其对应的拉普拉斯矩阵L为可逆矩阵，由引理6可知L͂为正定矩阵。

在实际应用中，基于事件触发的控制协议还需要保证事件触发时间间隔τ>0,以确保整个多智能体系统在收敛过程中，不会在某一时间段内无限次触发控制协议，即避免Zeno行为发生。

定理2若假设1成立，通过应用控制协议（3）和事件触发函数（4），所有智能体均排除了Zeno行为的发生，且事件触发时间间隔τi满足以下条件：

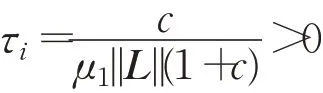
其中

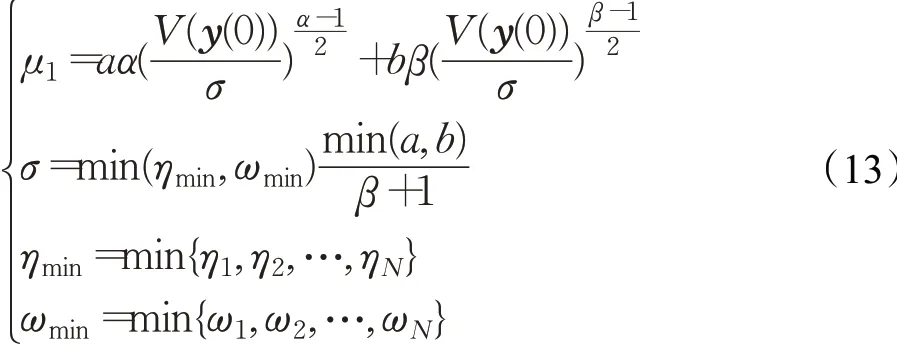
证明类似于文献[23]，定义：

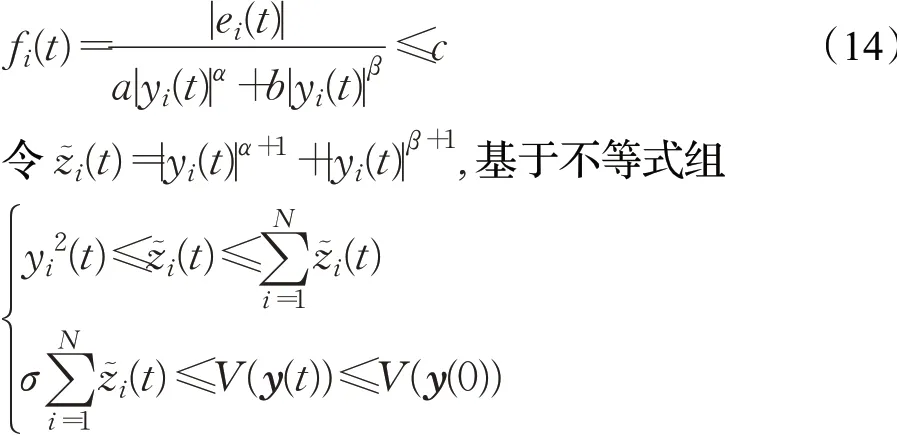
对式（14）关于时间t求导，可得：

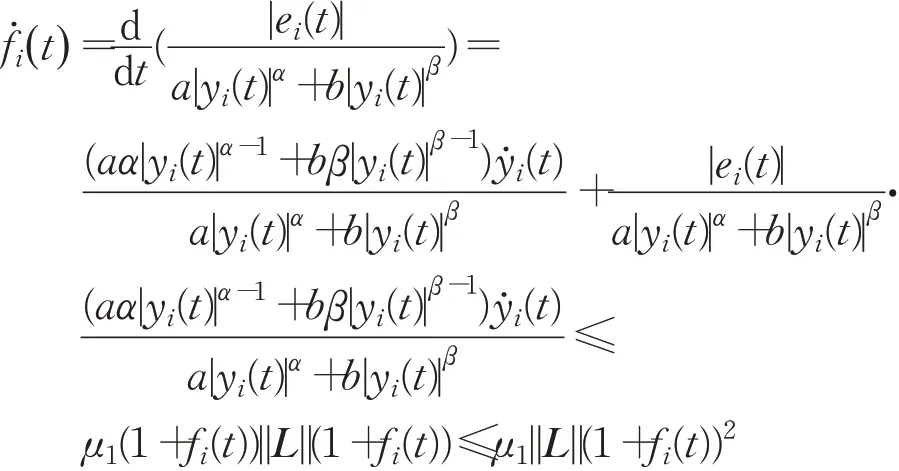
其中μ1的定义见式（13）。

对式（15）求解得：

将式（16）化简，可得触发时间间隔τi的表达式为：

因此，通过使用控制协议（3）和触发函数（4），多智能体系统（2）中的所有智能体均有效避免了Zeno行为的发生。证毕。

注6本文在文献[15]的工作基础上，进一步研究了多智能体系统的二分一致性问题。相比文献[15]中采取的连续控制策略，本文提出的基于事件触发机制的控制方法有效降低了系统控制过程中的能量消耗，并避免了Zeno行为的发生。

3 仿真

本章将通过数值仿真来验证本文所得理论结果的有效性。

考虑由六个智能体组成的一阶多智能体系统，其拓扑关系图如图1所示，其中图1（a）为结构平衡图，图1（b）为结构不平衡图。图1（a）和图1（b）的邻接矩阵分别为：

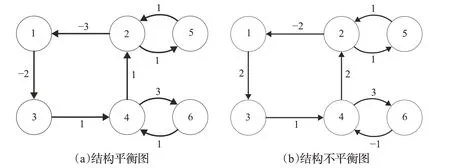
图1 拓扑图Fig.1 Topological graphs

和

选择控制增益和参数分别为a=0.1,b=0.2,α=0.8和β=1.2,设置事件触发函数参数c=0.5,当系统初始状态为X(0)=[-10,8.7,2.3,-1.5,5.5,-7.3]T时，图2和图3分别显示的是具有强连通拓扑结构的多智能体系统中各智能体的位置轨迹和事件触发时刻。可以发现，无论拓扑图是结构平衡图还是结构不平衡图，多智能体系统均可在固定时间内实现二分一致性。图4显示的是各智能体的控制输入随时间变化的趋势。由图4可知，当拓扑图为强连通图时，各智能体的控制输入均为分段函数，避免了能量的持续输出，减少了系统的能量损耗。

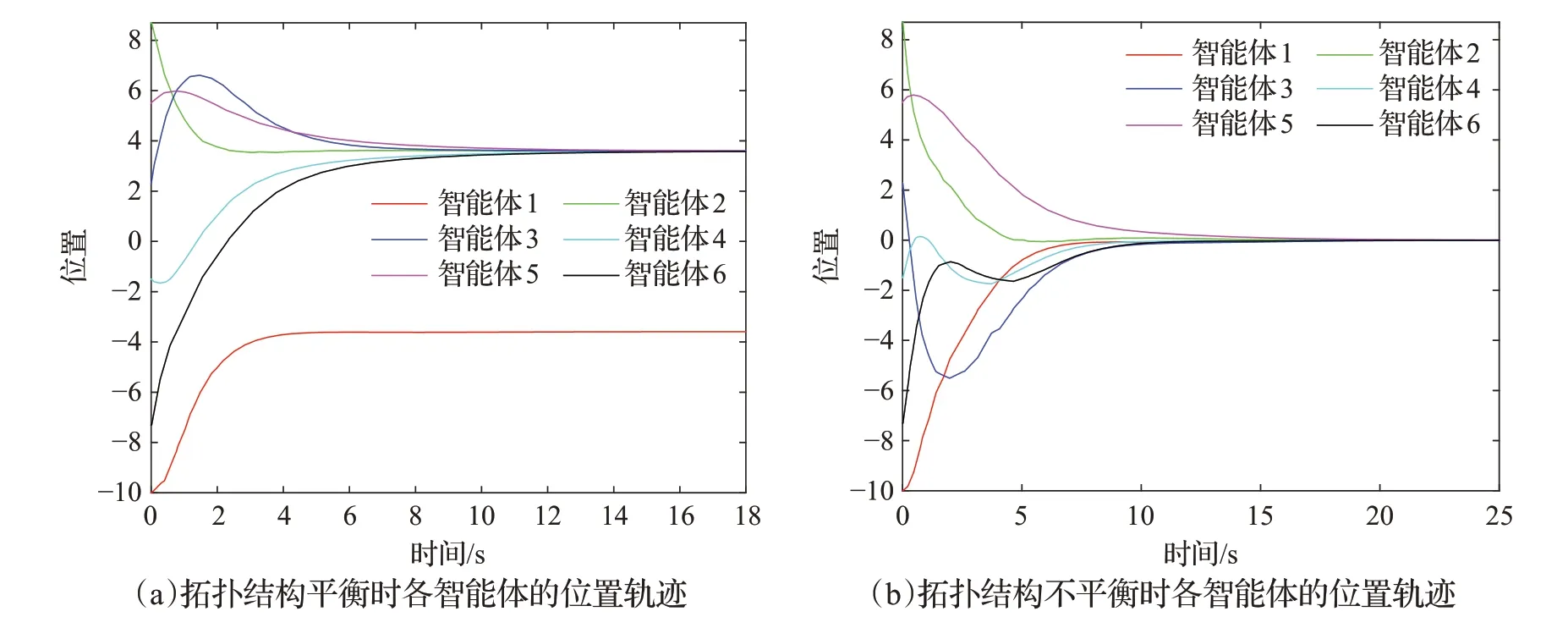
图2 智能体位置状态轨迹图Fig.2 Trajectories of position states

图3 各智能体事件触发时刻Fig.3 Triggering instants of all agents

图4 智能体控制输入Fig.4 Control inputs of all agents

4 结语

本文研究了具有符号有向图的一阶多智能体系统的固定时间二分一致性问题。通过设计基于事件触发机制的控制协议，以图论和Lyapunov理论为主要研究工具，证明了多智能体系统中所有智能体状态的绝对值均可在固定时间内实现一致，且在控制过程中有效避免了Zeno行为的发生。基于事件触发机制设计的控制协议避免了对智能体的连续控制，有效降低了能量损耗。