泊松方程的有限差分方法及快速实现

刘 昊，张荣培，霍俊蓉

（沈阳师范大学 数学与系统科学学院，辽宁 沈阳 110136）

泊松方程是常见于静电学、机械工程和理论物理的偏微分方程，在无引力源的情况下，ΔΦ=0（即拉普拉斯方程）；当考虑引力场时，ΔΦ=f（f为引力场的质量分布）。该方程通常用格林函数法求解，也可以采用分离变量法和特征线法求解［1］。

带有规则区域Dirichlet边界条件的泊松方程：

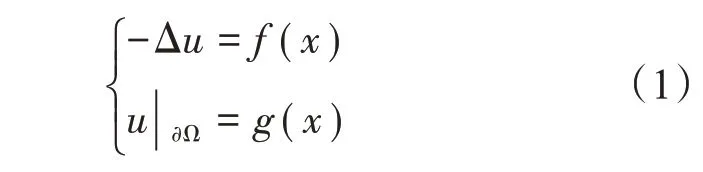
式中，Δ 表示拉普拉斯算子；x∈Ω；Ω ⊂Rd；当d=1时，Δu=uxx；当d=2 时，Δu=uxx+uyy；当d=3 时，Δu=uxx+uyy+uzz。

由于带有Dirichlet 边界的泊松方程的解析解不容易求出，一般情况下采用有限差分法、有限元法和有限体积方法的数值方法进行求解［2-4］。但这些方法在求解过程中需要求解大型的非线性代数方程组，计算过程复杂，耗费时间较多。

综上所述，本文提出了一种格式构造简单、发展比较成熟的有限差分方法，可求解一维、二维和三维情形下的泊松方程，针对每一种情形分别采用直接求解方法和快速离散正弦变换方法进行求解。

1 预备知识

将一维、二维和三维情形的求解区域、网格步长和数值解矩阵统一列在表1中。

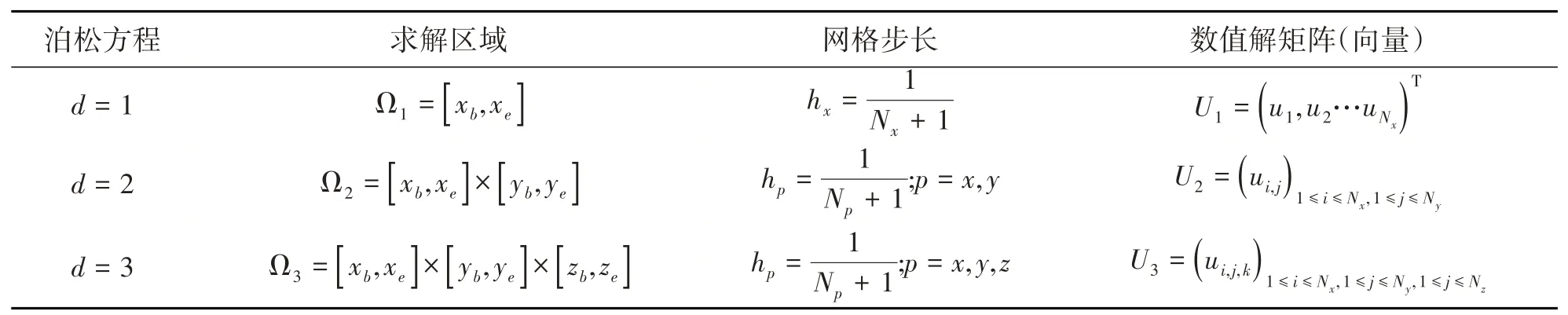
表1 d维泊松方程的求解区域、网格步长和数值解矩阵

对式（1）做有限差分离散，所得有限差分矩阵Gp如下：

式中，p=(x,y,z)。该矩阵可以做如下特征分解：

定理1有限差分方程的微分矩阵Gx可进行对角化［6］：

式 中，Λx=diag。对Gy和Gz也可得类似的结果。Sx是正弦矩阵，Sx与向量v 做乘积相当于对v进行离散正弦变换，可以结合傅里叶变换来实现，使得计算复杂度降低为O(Nxlog2Nx)。此时，Sx还是一个正交矩阵，即Sx=Sx-1。

由于二维和三维情形的有限差分矩阵需要用Kronecker积（⊗）得到，为了将其对角特征分解，需要用到下列Kronecker积的性质：

定理2对矩阵A、B、C、D以及Kronecker 积（⊗）的性质［5］：

1）(A⊗B)(C⊗D)=AC⊗BD；

2）(A⊗B)-1=A-1⊗B-1；

3）(BT⊗A)Vec(X)=Vec(AXB)；

4）(A⊗B)T=AT⊗BT。

2 有限差分

2.1 一维情形

采用二阶中心差分得到差分格式，将式（1）中的拉普拉斯算子进行泰勒展开：

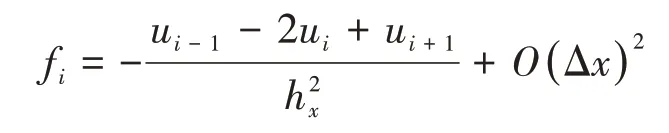
离散后为

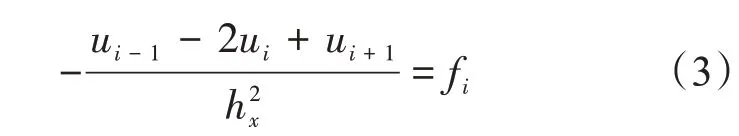
式中，fi为源函数；i∈Nx；fi=f(xi)的两个边界值为g(xb)和g(xe)，放在右端项中。

如果式（1）在x、y、z方向的Dirichlet边界，那么在边界处不会存在奇性。由于式（1）的边界条件满足以上假设，故不存在边界交叉点处的奇性。

将式（3）改写成矩阵形式：

令K1d=-Gx，则

式中，右端向量F的定义如下：

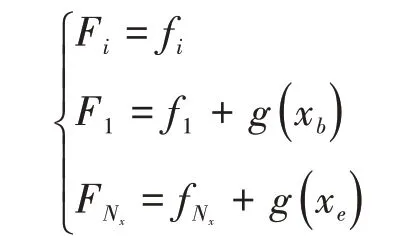
式中，i∈(2,3,…,Nx-1)。

由于Gx是三对角矩阵，故可使用追赶法［6］求解式（4）。此外，还可以采用离散正弦变换方法求解。由式（3）可得

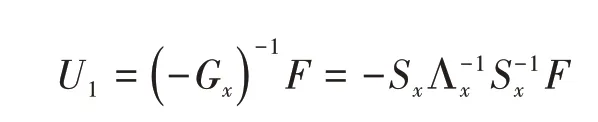
上式可由3步来实现：

1）V1=Sx-1F可采用逆离散正弦变换实现；

2）对于V2=Λx-1⋅V1，由于Λx是对角矩阵，所以只有Nx次乘除法的计算过程较为复杂；

3）V=-SxV2采用离散正弦变换实现。

由于追赶法的计算复杂度为5Nx-4［7］，但离散正弦变换方法中的1）步和3）步的计算复杂度大约为O(Nxlog2Nx)［7］。由此可见，一维情形追赶法的计算方法具有优势。

2.2 二维情形

采用二阶中心差分算子，将式（1）中的拉普拉斯算子进行泰勒展开：

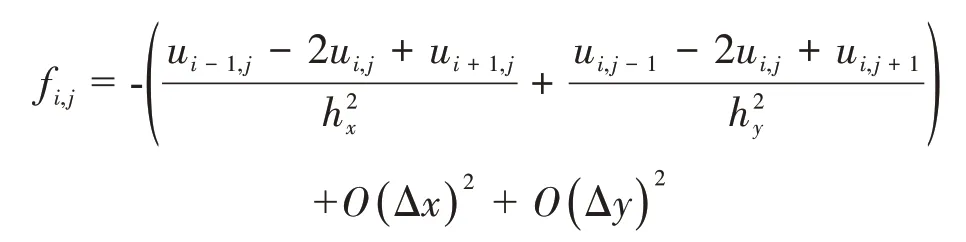
式（1）的差分格式如下

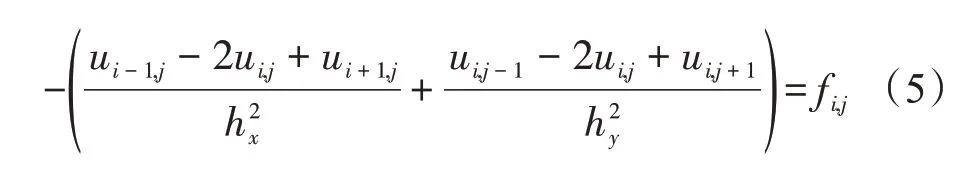
设Ip为Np阶单位矩阵，将解矩阵U2向量化后得

根据Kronecker积的定义，式（5）的二阶中心差分格式可以写成如下形式：

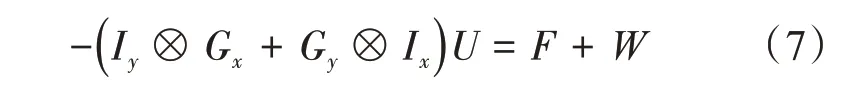
式中，F=vec(F)；矩阵F的元素由源函数得到；Fi,j=f(xi,yj)；i∈(1,…,Nx)；j∈(1,…,Ny)；边界项W=vec(Ux1+Uy1)。

Ux1和Uy1的元素由边界值来确定：

式（8）同样可以采用高斯消去法和离散正弦变换法求解。对K进行特征分解，由于利用Kronecker积的性质可得：

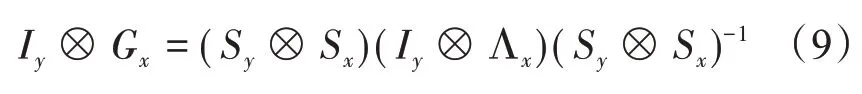
对Gy⊗Ix可做类似运算，则

上式可由以下3步来实现：

1）利用Kronecker 积的性质对式（8）右端项进行拉直变换：

再应用逆离散正弦变换实现：

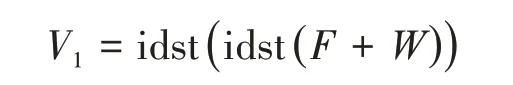
2）对于V2=，./为矩阵中每个元素相除，这步计算的复杂度为Nx×Ny次乘除法；

3）U2=dst(dstV2)，即可直接采用离散正弦变换实现。

根据高斯消元法，当Nx=Ny=N时，其计算复杂度为O(N4)，但快速离散正弦变换方法中1）步和3）步的计算复杂度仅为O(N3)［8-9］。由此可见，离散正弦变换方法的计算速度具有优势。

2.3 三维情形

三维情形下将式（1）中的拉普拉斯算子进行泰勒展开：

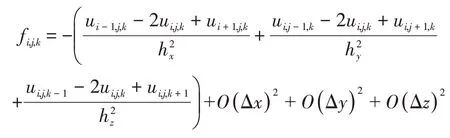
式（1）的二阶中心差分格式如下：

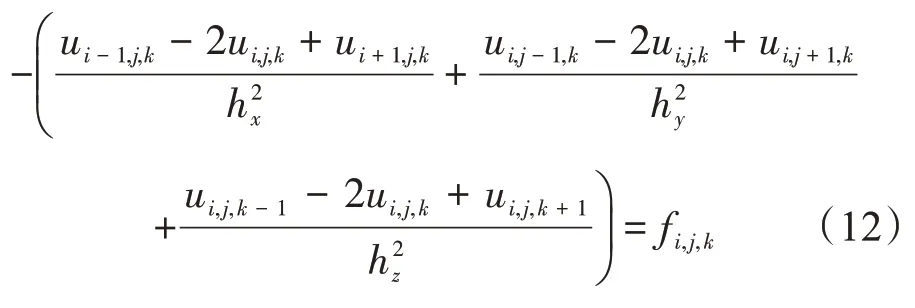
将解矩阵U3向量化后得

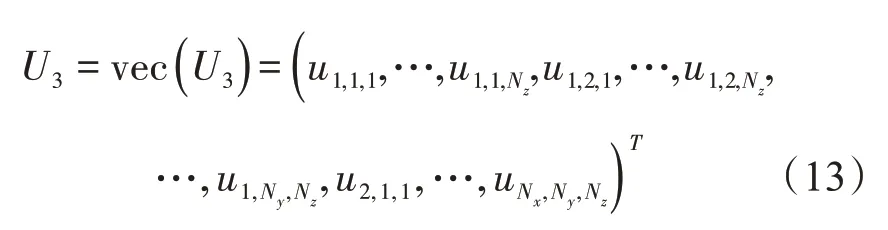
利用Kronecker 积定义，式（12）的差分格式可改写为

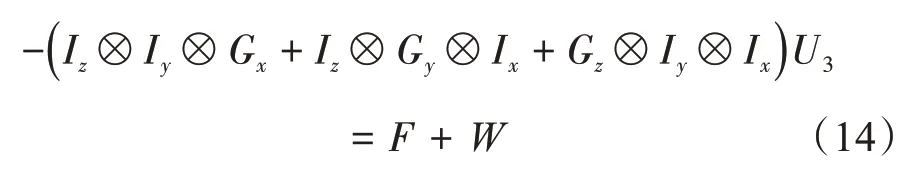
式中，Fi,j,k=f(xi,yj,zk)，i∈(1,…,Nx)；j∈(1,…,Ny)；k∈(1,…,Nz)；Ip为Np阶单位矩阵；p=(x,y,z)；W由边界值来确定，且W=vec(Ux1+Uy1+Uz1)。

Ux1、Uy1和Uz1的元素由边界值确定：

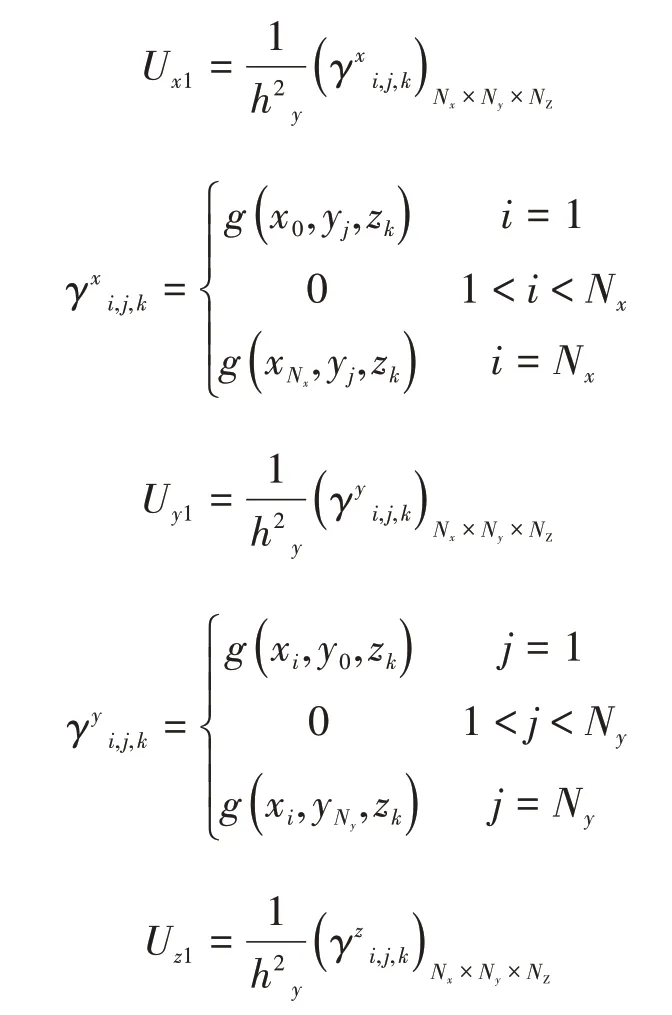
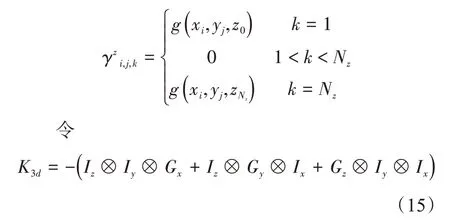
故可将差分格式（14）改写为

式（16）有两种解法：第一种是利用高斯消元法直接求解式（15）；第二种利用离散正弦变换方法，对K3d进行矩阵分解：

三维数组U3可以被视为二维数组上所有这样的一维向量的集合，即

式中，U3(:,j,k)是通过固定最后两个指标j和k得到的Nx维向量。

由式（18）分解可得

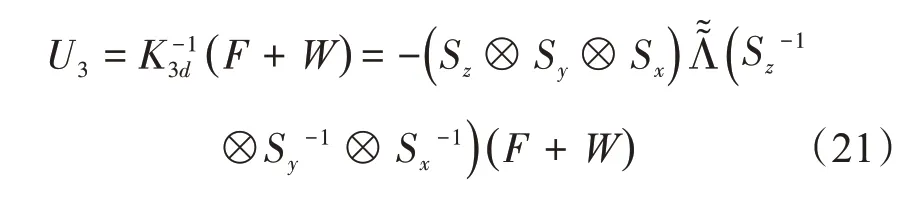
式（21）可通过如下3步实现：

1）应用逆离散正弦变换得到向量V1=，若将U3视为二维数组上的一维向量的集合，则有

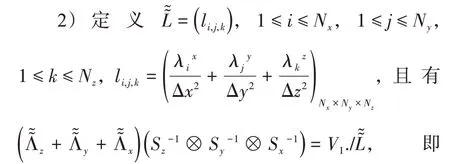
3）直接应用离散正弦变换实现，若将U3视为二维数组上的一维向量的集合，则有

由于积分的部分采用梯形求积公式进行离散，故精度为二阶精度。

在上述实现过程中，利用高斯消元法求解三维泊松方程时，其计算量为O(N7)［7］，但在快速离散正弦变换方法中，1）步和3）步的计算复杂度仅为O(N2log2N)［7］。由此可见，离散正弦变换方法的计算速度极具有优势。

3 数值实验

针对d维齐次泊松方程，一维情形下选取精确解函数为u(x)=π2sin(πx)，结果如表2 所示；二维情形下选取精确解函数为u(x,y)=2π2sin(πx)sin(πy)，结果如表3 所示；三维情形下选取精确解函数为u(x,y,z)=2π2sin(πx)sin(πy)sin(πz)，结果如表4所示。

表2 一维情形下使用快速离散正弦变换和使用追赶法的误差、误差阶及时间比较

表3 二维情形下使用快速离散正弦变换和使用追赶法的误差、误差阶及时间比较

表4 三维情形下使用快速离散正弦变换和使用追赶法的误差、误差阶及时间比较

上述结果表明，本文提出的快速正弦离散变换方法具有更高的效率。

4 结语

本文应用快速离散正弦变换求解泊松方程，该方法能够在二维和三维的情况下快速地求解离散后得到的非线性代数方程组，提高了计算效率。实验结果表明：在一维情形时，在同样的精确度下利用追赶法直接求解泊松方程的计算时间较快，正弦离散变换方法的速度较慢；但在二维和三维的情形下，快速正弦离散变换法的计算时间更短，计算次数更少，计算复杂度更低，且同样可以达到较高的精确度。