基于迭代思想的同杆双回线单相接地故障定位方法
徐明阳,刘益青,邢志超,薛嘉慧,朱一鸣
(1.济南大学自动化与电气工程学院,山东 济南 250022;2.积成电子股份有限公司,山东 济南 250100)
0 引言
随着我国电网规模的不断扩大,环境保护形势也日益严峻[1-3]。同杆双回线输电容量大、建设速度快、节约成本,因此在工程上被日益广泛的应用[4-5]。距离保护具有灵敏度高,较少受系统运行方式影响等优点[6],用作同杆双回线的主保护。当故障发生时,距离保护首先确定故障相[7],然后故障定位,区内故障时保护跳闸切除故障。在故障定位阶段,同杆双回线因两回线距离较近,两回线电气量相互耦合,导致线间零序互感较强。而在实际工程中,同杆双回线配置单回线、单间隔距离保护方案[8],未引入相邻回线的电压电流;而且为了线路保护的独立性,不能引入邻线电压电流。因此当同杆双回线配置单回线、单间隔距离保护时,受零序互感的影响,故障定位不准确。由于同杆双回线单相接地故障占全部故障的80%[9],线间互感可达线路自感的50%~70%[10],单相接地故障发生概率大且对本线距离保护影响最大。因此,当接地距离保护应用于同杆双回线中,且按单回线、单间隔配置时,研究出一种新型的故障定位方法尤为重要。
目前,解决同杆双回线线间互感对单回线、单间隔配置距离保护故障定位影响的方法主要有两类。第一类为直接采集相邻回线电压电流的故障定位方法。此类方法是通过利用同杆双回线两回线的故障信息确定出故障位置,且大部分是基于六序分量法[11]。文献[12]提出了一种同向正序基频分量的双回线故障定位新原理。基于分布参数模型,文献[13-14]提出了一种单端定位方法,可以实现同杆双回线跨线接地故障的准确定位。虽然第一类方法定位出的故障位置较为准确,但是破坏了线路距离保护的独立性,降低了线路距离保护的可靠性。
第二类为不直接采集相邻回线电压电流的故障定位方法。由于影响同杆双回线故障定位的零序互感由相邻回线零序电流产生,因此此类方法通过估算出相邻回线的零序电流,从而消除线间零序互感对距离保护故障定位的影响。文献[15-16]提出了利用切换定值域整定距离保护零序补偿系数的策略。文献[17-19]首先根据估算出的近似故障位置估算出了相邻回线的零序电流,从而提出新的接地故障定位算法。但是文献[15-19]只是粗略估算出相邻回线零序电流,只能减小线间零序互感对距离保护故障定位的影响,不能从根本上消除零序互感的影响,因此在实际应用过程中仍存在很大的误差。
由于当前相邻回线零序电流的估算精度低而不能消除线间零序互感对距离保护的影响,导致无法准确定位出故障位置,因此需要研究一种提高相邻回线零序电流估算精度从而准确确定故障位置的方法。基于牛顿迭代思想,提出一种新型的同杆双回线单相接地故障定位方法。该方法利用牛顿迭代法来提高相邻回线零序电流的估算精度,从而准确确定故障位置,并通过PSCAD仿真验证了所提方法的性能。
1 同杆双回线接地故障的牛顿迭代法
同杆双回线输电系统模型如图1 所示,其中故障设置为第I回线的单相接地故障。图1中分别为同杆双回线M 侧与N 侧的等效电源;ZM与ZN分别为同杆双回线M 侧与N 侧的等效电阻;保护安装在I回线M侧;K1、K2、……、K21为不同故障点。

图1 同杆双回线故障模型
同杆双回线单相接地故障等效模型如图2所示。

图2 单相接地故障等效模型
图2 中,K为故障点;分别为I 回线M 侧保护测量到的故障相φ的电压、电流以及零序电流;为II 回线M 侧保护测量到的零序电流;Z1、Z0分别为同杆双回线线路全长的正序阻抗与零序阻抗;Z0m为同杆双回线线路全长的线间零序互感抗;D为输电线路保护安装处到故障位置的距离与输电线路全长的比值,因此D∈[0,1];为故障点流向大地的故障电流;RK为过渡电阻。
将互感抗Z0m解耦到母线M 侧,根据保护安装处至故障点处的故障回路列写基尔霍夫电压定律(Kirchhoff′s Voltage Law,KVL)方程,整理可得I回线M侧故障相电压为

式(1)中,由于Z0、Z1和Z0m这3 个量是输电线路固有参数,这3个量可以由I回线M 侧保护处测量得到,因此以上都是已知参数。但是由于I 回线保护无法获取II 回线的电气量,因此是未知参数;此外,同杆双回线接地故障时,过渡电阻RK是未知的;故障点对地电流无法测量,是未知的;D为待计算的故障位置,也是未知的。因此式(1)中存在和D这4个未知参数,无法直接求解。若要确定出故障位置,即令方程中最多只存在D这一个未知量,可通过分析与D的关系以及消去未知量RK,将式(1)表示为以故障位置D为未知量的方程。

同杆双回线单相接地故障时零序故障解耦网络如图3 所示。图3 中,ZM0与ZN0分别为M 侧与N 侧系统的等效零序阻抗,为故障点对地零序电流,为I回线N 侧保护安装处测量到的零序电流,与分别为回路1、回路2、回路3与回路4的电流。

图3 单相接地故障零序故障解耦网络

根据电路原理列写出2个辅助方程为




运用KVL,根据图3 中回路2 与回路4 列出2 个方程为


3)实虚部分离消除未知量RK。
将式(8)代入式(1)中,可得

式(11)中,参数RK与D为实数,参数、Z0、Z1、Z0m与CΙ0为复数。因此,为了消除含RK的项,需要将式(11)中的实部与虚部分离。
令式(11)两端同时乘以CΙ0以及的共轭,即可实现实部与虚部分离,即为


式(13)中,由于CΙ0也含有未知量D,因此无法直接求得故障位置D的精确解,本文提出采用牛顿迭代法求解。
首先构建出牛顿迭代公式,为了令根的近似值逐步逼近于精确解,接下来需要利用牛顿迭代公式反复校正根的近似值,最后得到满足一定精度要求的结果。
假设方程f(x)=0,将f(x)=0同解变换为

若x*为f(x*)=0 的精确解,也就是方程f(x)=x-φ(x)=0 的解。假定f′(x)≠0,利用泰勒级数展开可得到牛顿迭代方程[17]为
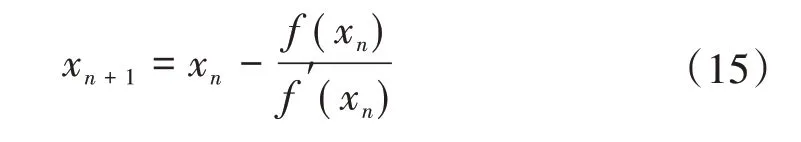
式中:n=0时x0为初值。
式(15)所示的牛顿迭代方程需要保证f′(x)≠0,其迭代收敛条件为f(x)f″(x)>0[20]。
根据式(15)对式(13)进行变换,即可得到故障定位牛顿迭代方程为

式中:D(n)为第n次迭代值;D(n+1)为第n+1 次迭代值。
2 同杆双回线单相接地故障定位方法
同杆双回线单相接地故障定位方法的迭代计算流程如图4 所示,流程中两个重要的环节为确定合理的迭代初值和迭代停止条件。
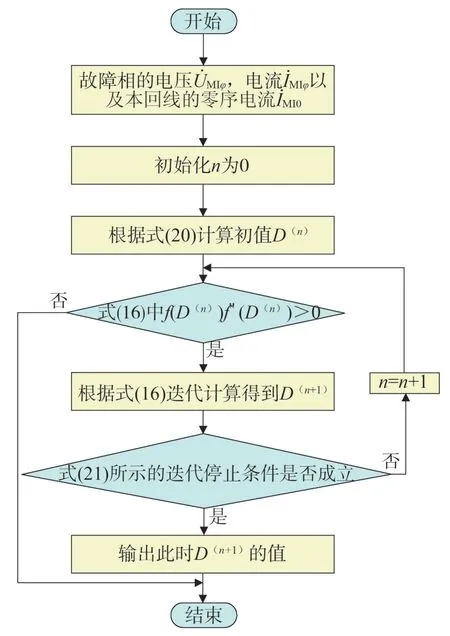
图4 故障定位算法迭代计算流程
2.1 迭代初值的选取
迭代过程需要确定合理的初值,初值不合适可能导致迭代不收敛,因此初值选取应尽量接近精确值。以故障位置D的估算值作为迭代初值。由于故障发生在不同位置时,不同,为了保证迭代的收敛性,故障位置D的估算值这一迭代初值的选取与精确值应尽量接近,采用当输电线路发生末端故障时,即D=1 时的值来代替任意位置发生故障时的值,而同杆双回线线路末端发生故障时=。
将式(1)中的阻抗用电阻和电抗的形式进行表示,整理得

式中:R1、X1分别为输电线路全长的正序电阻与正序电抗;R0、X0分别为输电线路全长的零序电阻与零序电抗;R0m、X0m分别为输电线路全长的线间零序互电阻与线间零序互电抗。
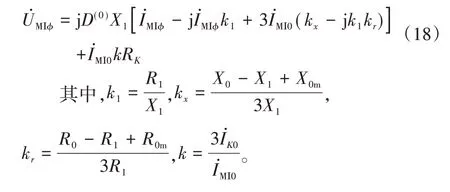
由于高压线路中,线路阻抗主要呈现为感性,而输电线路故障发生时,分流可得到。因此,式(18)中k=/可认为是实数。那么令,即,将式(18)进行等效并分离实虚部,可整理为

其中,
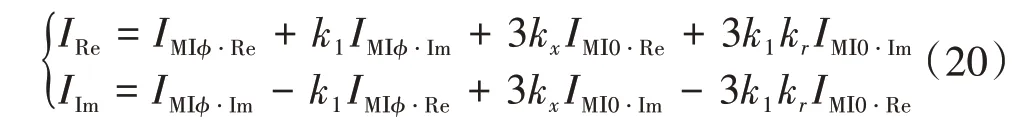
式中:UMΙφ⋅Re为的实 部;UMΙφ⋅Im为的虚部;的实部;的虚部。
求解式(19),消去R′K就可得到迭代初值为
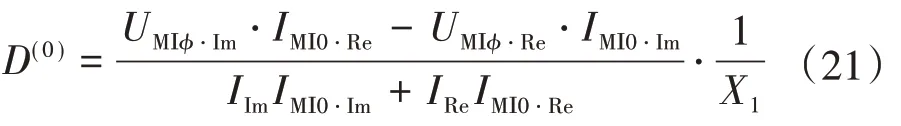
2.2 迭代停止条件
在迭代过程中,如果迭代计算的结果达到了预先设定的精度,那么就停止迭代,然后输出迭代计算结果。本文设置的迭代停止条件为
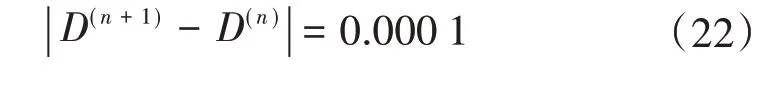
3 仿真分析
对提出的基于牛顿迭代思想的同杆双回线单相接地故障定位算法进行仿真分析与性能验证。在PSCAD 中搭建如图1 所示的同杆双回线故障仿真模型,同杆双回线单位长度线路参数为:z1=0.022 +j0.280 Ω/km、z0=0.182+j0.860 Ω/km,单位长度互感为z0m=j0.140 Ω/km。M、N 侧系统电源等值参数为:Z0M=j7.8 Ω、Z0N=j18.2 Ω。
分别在同杆双回线I 回输电线路全长的0%、10%、30%、50%、80%以及100%处设置故障,故障类型设置为单相接地故障;每一个故障点处过渡电阻分别设置为0 Ω(金属性故障)、20 Ω、150 Ω 以及300 Ω;将故障起始时刻设置为t1=0.4 s,故障持续时间设置为t2=0.3 s,仿真验证本文所提的基于牛顿迭代思想的同杆双回线故障定位算法。
首先利用MATLAB 读取由PSCAD 仿真得到的故障录波数据,然后仿真分析故障定位算法。经验证发现3 种相别的单相接地故障仿真结果的相对误差相近,因此本文以A 相接地故障(AG)故障为例,列出并分析仿真结果。
不同故障位置以及过渡电阻的仿真验证结果如表1—表4 所示,可根据式(23)计算得出表中的相对误差ρ。

表1 金属性故障时的故障定位算法验证结果
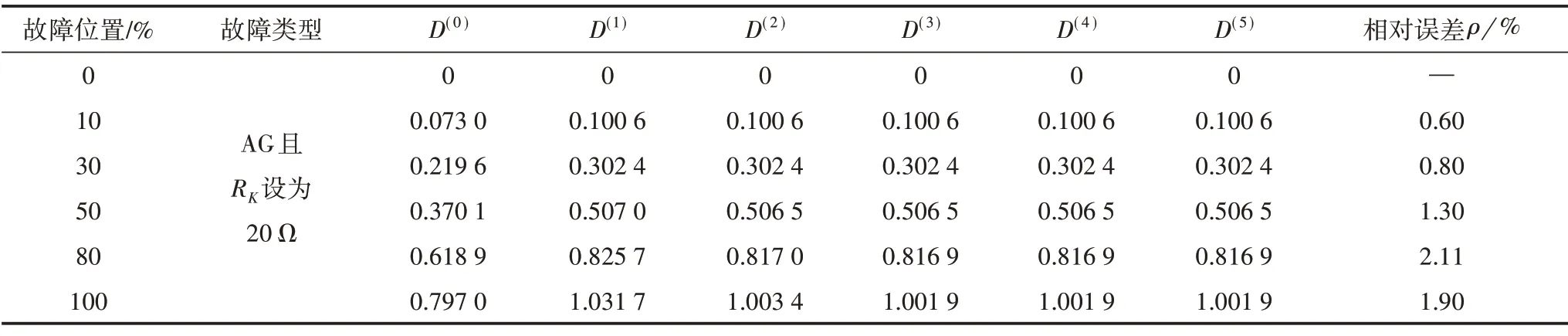
表2 20 Ω过渡电阻时的故障定位算法验证结果
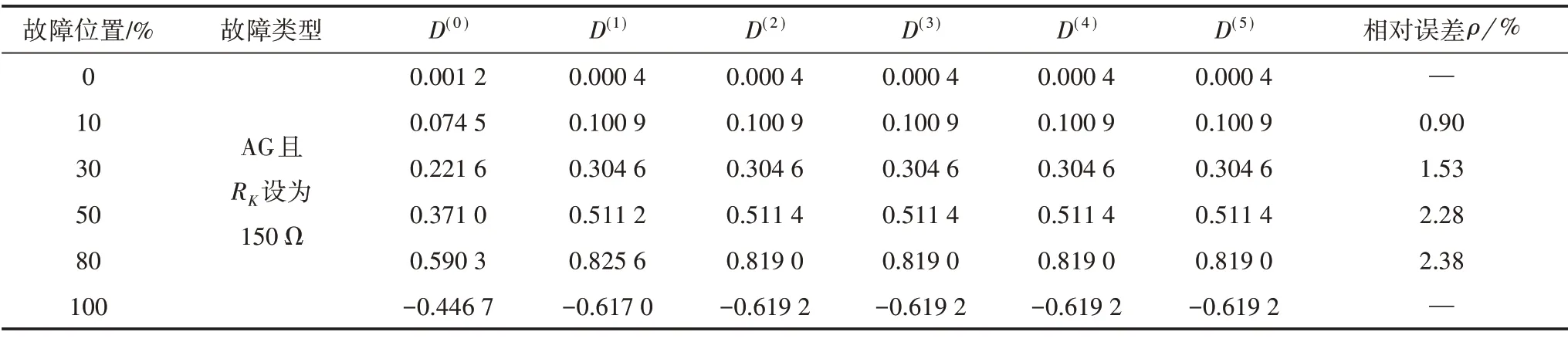
表3 150 Ω过渡电阻时的故障定位算法验证结果

表4 300 Ω过渡电阻时的故障定位算法验证结果
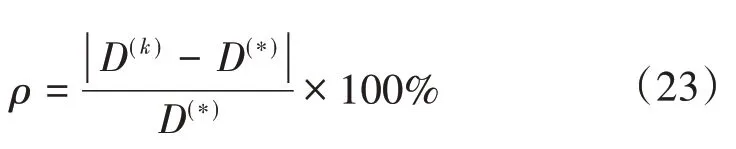
式中:D(k)为第k次迭代值;D(*)为仿真设置的故障位置的精确值。
根据表1 与表2 数据,当过渡电阻较小时,本文所提出的基于牛顿迭代思想的故障定位算法在计算过程中均收敛,而且收敛速度较快,最多只需要4 次迭代计算就能够准确确定出同杆双回线线路全长任意单相接地故障的故障位置。根据表3与表4数据,当过渡电阻较大时,线路全长80%以内发生故障时的验证结果亦是如此。但是当线路100%处发生单相接地故障时,所提故障定位算法收敛到了错误值。
接下来进一步分析并解决当线路100%处发生单相接地故障时,所提算法收敛到错误值的问题。
当线路发生故障时,根据式(16)迭代计算出的故障位置,相当于在直角坐标系中求解出式(16)中f(D)函数与x轴相交交点的横坐标。例如,同杆双回线I 回输电线路全长的30%位置处发生A 相接地故障,且过渡电阻为150 Ω 时,y=f(D)的函数图像如图5 所示。此时函数y=f(D)与x轴有1 个交点,即方程f(D)=0 的解正好是交点的横坐标,因此所提出的基于牛顿迭代思想的故障定位算法在迭代过程中,会向着方程f(D)=0的解逐步收敛。

图5 线路30%处故障时f(D)的曲线
当I 回输电线路100%处发生A 相接地故障,且过渡电阻为150 Ω 时,y=f(D)的函数图像如图6 所示。此时函数y=f(D)与横轴的交点有2 个,即方程f(D)=0 的解有2 个。在图6 中,由于交点D1与交点D2的邻域内均符合公式f(x)f″(x)>0,满足了迭代收敛条件,因此可以通过迭代计算分别求解出y=f(D)函数图像的拐点以左与拐点以右区域中方程f(D)=0 的解,即图6 中的D1与D2。但是由于迭代初值选取不当,致使故障位置落在函数图像拐点以左的区域中,因此导致迭代结果收敛于方程f(D)=0 与x负半轴交点的横坐标上,即图6 中的D1,进而导致迭代计算得出的故障位置错误。

图6 线路100%处故障时f(D)的曲线
由仿真得出,当线路末端发生单相经150 Ω 与300 Ω过渡电阻接地故障时,所提出的基于牛顿迭代思想故障定位算法都会由于选取的迭代初值不合理,使得迭代计算出的结果最终收敛于方程f(D)=0与x负半轴交点的横坐标上。
因此,针对初值选取不当导致的故障位置落在函数图像拐点以左的区域中,进而使得最终的迭代计算结果收敛到错误值这一问题。本文规定,迭代计算过程中,当迭代计算结果是负数时,应调整迭代初值为1,即设置D(0)=1,然后重新进行迭代计算,最终实现准确故障定位。
重新设置迭代初值为D(0)=1 后,当线路末端发生单相经150 Ω 与300 Ω 过渡电阻接地故障时的迭代计算结果如表5所示。

表5 设置迭代初值为1后的故障定位迭代算法验证结果
通过分析以上不同过渡电阻以及不同故障位置的迭代计算结果,本文所提基于牛顿迭代思想的故障定位算法仿真验证结果为:
1)当同杆双回线线路全长的80%以内发生单相接地故障时,所提算法在迭代过程中收敛速度快,能够仅利用单回线电气量消除零序互感的影响,实现准确故障定位。
2)当同杆双回线线路末端发生单相接地故障时,所提算法在迭代过程中收敛速度快,仅需要通过调整初值为D(0)=1,就可以利用单回线电气量消除零序互感对故障定位的影响,实现准确故障定位。
4 结语
当接地距离保护直接应用于同杆双回线中,且按照单回线、单间隔配置时,不能消除相邻回线零序互感对故障定位的影响,继而导致不能准确确定故障位置。针对不直接采集相邻回线电压电流的同杆双回线故障定位方法,不能准确确定故障位置这一问题,提出了一种新型的基于牛顿迭代思想的同杆双回线故障定位方法。通过对同杆双回线单相接地故障进行分析,利用牛顿迭代法来提高相邻回线零序电流的估算精度,仅利用单回线电气量就能准确故障定位,并通过仿真验证了所提方法的性能。仿真结果表明,在不同故障位置与过渡电阻下,所提算法在迭代过程中的初值选取方便、收敛速度快,仅利用单回线电气量就能准确故障定位,其定位精度虽不及直接采集相邻回线电压电流的方法,但却远高于不直接采集相邻回线电压电流的方法。然而,本文只考虑了同杆双回线的单回线单相接地故障的情况,下一步将继续研究将本方法扩展到其他故障类型。

