一种基于GA具有最大动载的车用圆锥滚子轴承优化方法

徐辉，侯建伟，卢彦群

一种基于GA具有最大动载的车用圆锥滚子轴承优化方法

徐辉，侯建伟，卢彦群*

（河北工程大学，河北 邯郸 057000）

设计方法对汽车圆锥滚子轴承的性能、寿命和可靠性具有重要影响，从而也影响着使用该类轴承的汽车产品的工作性能和经济性能，因此，从所有可能的设计方案中找到一种最佳选择就显得十分重要。该研究从挖掘圆锥滚子轴承的最大动载荷入手，采用遗传算法（GA）设计具有较高性能的车用圆锥滚子轴承，研究过程中既满足了所有的边界条件，也获得了一个很大的多维搜索空间；研究结果表明，当搜索并迁移到一个更适宜的区域时，在该区域内轴承具有更高的额定动载荷，而且随着违例行为的增多，惩罚值呈指数增长，而对每一个违反约束的行为都进行一些惩罚，就可以得到更高的额定动载荷。所以，该研究为提高滚子轴承的最大动载荷，进而提高其使用性能和寿命找到了一种简便快捷的方法，为轴承设计提供了一种新的途径。

车辆；圆锥滚子轴承；最大载荷；遗传算法；优化设计

引言

对汽车而言，一项基本需求就是使其滚动轴承具有承受最大动载荷的能力，这意味着在设计中尽量使轴承所承受的动载荷最小化[1-2]。动载荷可由下式表示：

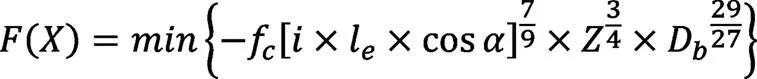
其中：

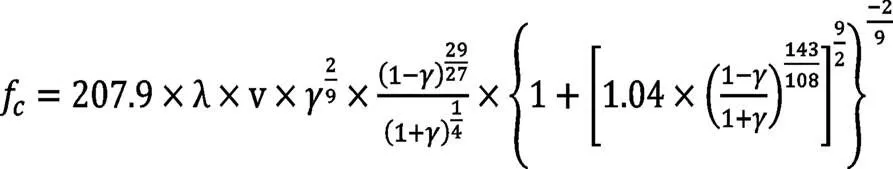
式中：、分别取0.65和1.2；=Dm×cocα/D（D为轴承节径；为接触角；D为滚子平均直径）；为滚子列数；l为滚子的有效长度；为滚子数；这里，D、D、l、、为轴承的设计参数，可通用设计变量来表示，而轴承的外形尺寸可分别用（外径）、（内径）、（内圈宽度）、（外圈宽度）、（总宽度）来表示。

设计目标是获得满足特定边界条件的、使（）最小化的设计参数。

1 约束条件

设计过程中受到的约束条件有以下几个：

（1）约束1：

其中：

式中，为滚子锥角之半，而：

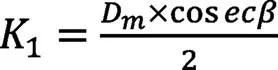
可由下式得到：

（2）约束2：

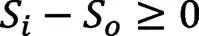
其中：

（3）约束3：

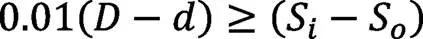
（4）约束4：

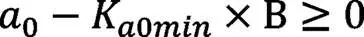
其中，0为内圈大挡边宽度；

K0为内圈大挡边宽度系数，这里K0min取0.15。

（5）约束5：

这里，K0max取0.20。

（6）约束6：

其中，1为内圈小挡边宽度；

K1为内圈小挡边宽度系数，这里K1min取0.05。

（7）约束7：

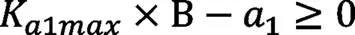
这里，K1max取0.10。

（8）约束8：

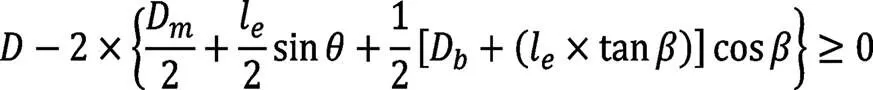
该约束（式10）确保滚子大端不会突出于轴承外圈；而约束1（式3）、约束2（式4）和约束3（式5）确保与滚子接触处内外圈的最小厚度[3]。

（9）约束9：

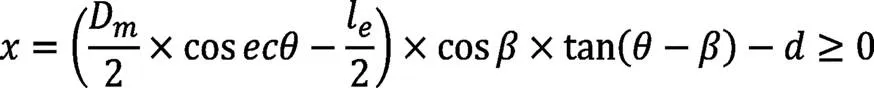
（10）约束10：

≥1° （15）

（11）约束11：

10°≤≤30≤ （16）

（12）约束12：

'0≥0.3 （17）

式中，'0为外圈大挡边宽度。

（13）约束13：

'1≥0.3 （18）

式中，'1为外圈小挡边宽度。

（14）约束14：

2min≥0 （19）

式中，C2min为内圈大端面轴向最小倒角尺寸。

（15）约束15：

3min≥0 （20）

式中，C3min为外圈大端面径向最小倒角尺寸。

（16）约束16：

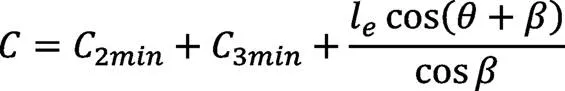
（17）约束17：

△≤0.002 （22）

式中，△为轴承总宽度误差，而总宽度可由下式计算：

（18）约束18：

0.8πD−D×≥0 （23）

轴承的设计参数必须遵循所有给定的约束条件。

2 目标函数

现在，我们来寻求一种具有最大动载承受能力且满足所有边界条件的圆锥滚子轴承的设计方案：尽管有一个非常大的多维搜索空间，但因为约束所丢弃的搜索空间也很大，而运算程序的目标是搜索并迁移到一个更加适宜的区域（比如：具有更大的动态额定动载荷）。也就是说，程序以增加动态荷载为目标而运行，同时满足所有约束。运行期间，对每一个违反约束的行为，都要施加一个惩罚，随着违规次数的增加，惩罚值呈指数增长[4-8]。

因此，有效目标函数，可用下式表示：

2.1 目标

−F' (X)=F(X) −Penalty （24）

2.2 运行

可以采用实数编码的遗传算法解决其运行问题，其单体结构包括以下几部分（如图1所示）：

图1 单体解决方案组成

图1中，D、D、l、为浮点数（实数），为整数。

2.3 流程

如图2所示。

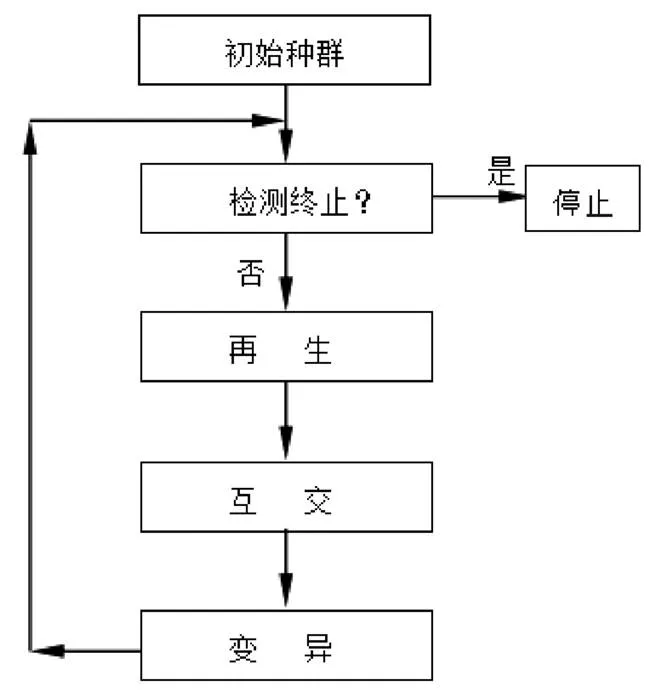
图2 算法流程

2.4 主要算子

该算法有以下三个主要算子——

（1）再生算子：在再生过程中，采用锦标赛式的选择方案，在每一次迭代中随机抽取个解，并把最优解传给下一代。

（2）交互算子：采用二级交互。一级交互通过将一个解决方案的变量与另一个解决方案的变量进行交叉来完成；二级交互通过同型实数之间相互交叉来实现。

（3）变异算子：有两种变异，一是随机地重置数字中的小数点，二是从实数中随机选取一个数字并用其补码来替换[9-10]。

2.5 程序文件

代码分布在5个程序文件中，用C语言编程。这5个程序文件如下：

（1）objective.h——该文件具有问题目标的基本结构，定义了方案构架和任何字段中的最大最小值。

（2）objective.c——该文件定义了目标函数及其约束条件，任何需要更改的问题，只需在该文件中进行。

（3）operator.h——此文件具有该项目中所有算子的函数原型。

（4）operator.c——此文件定义了实数编码算子。

（5）opti.c——这是调用所有函数和其他程序的主程序，它定义了主要变量，其他文件也可以访问这些变量。

3 技术细节

3.1 编程

编程可以通过任何C或C++编辑器来完成，如GCC、G++、C++、CC等。所有c文件都要用-o选项进行单独编辑，从而创建目标代码。

为了简化编译，可采用“maker.sh”文件，该文件在Unix命令提示符下运行时，可生成一个名为“exe”的可执行文件。（maker.sh的用法：Unix 命令提示符$./maker.sh；exe的用法：Unix 命令提示符$./exe。为清空项目工作区，采用“clean.sh”文件，这将使项目工作区返回原始状态。（同样，maker.sh的用法是采用Unix 命令提示符$.clean.sh）。m a k e r . s h

程序接受名为“input”的文件的输入指令，在输入文件中，变量的值在“$”符号之后读取。

3.2 运行结果

程序的运算结果就是圆锥滚子轴承的设计参数。文件的输出将存储在名为“输出”的文件中，这是输出便是众多方案中最好的解决方案。约束的频率可以在名为“惩罚”的文件中查看。

4 结论

程序的收敛速率很快，而且通过许多输入组合的测试，输出结果也令人满意。下面列举两种组合：

组合1：其输入、输出量及迭代效果分别见表1、表2和图3。

表1 组合1输入量

输入量DdBCTnetapcdimpm 数值$31.991$9.525$10.785$7.938$10.008$0.350$0.750$0.500$0.050

表2 组合1输出量

序列号DbDmleαZF(X) 14.01825.5818.32617.70716−14 784.595 24.94925.0528.20514.85912−15 006.972 34.94925.0528.20514.85912−15 007.128 45.54625.1168.10514.81212−15 947.692 54.36324.7958.48920.98213−13 885.619

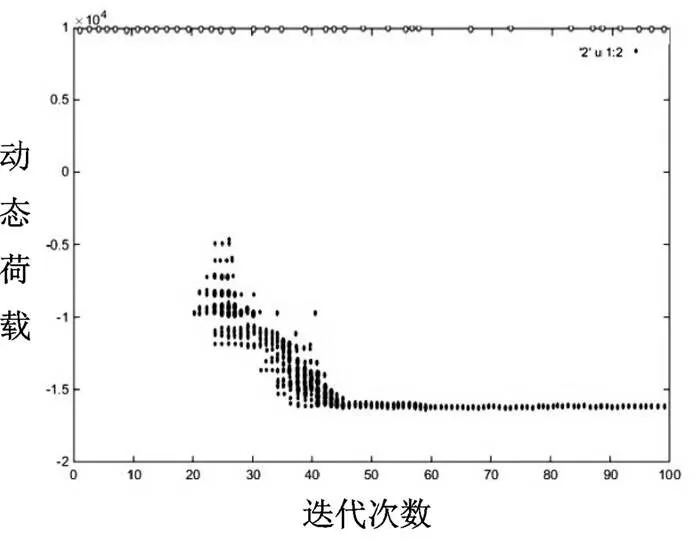
图3 组合1中的迭代效果

组合2：其输入、输出量及迭代效果分别见表3、表4和图4。项目的运行必修遵循前述一系列约束，通过记录违背约束的频度，可以探讨约束行为，并对其进行相应的排序。

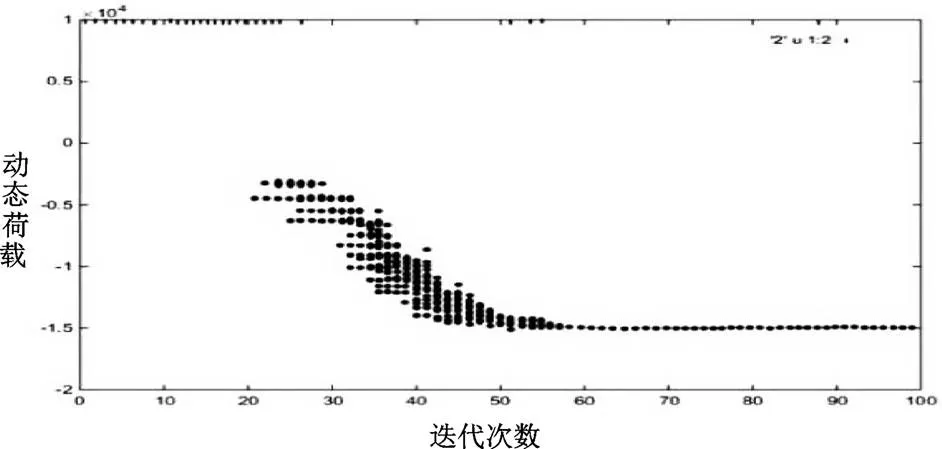
图4 组合2中的迭代效果

表3 组合2输入量

输入量DdBCTnetapcdimpm 数值$34.988$12.701$10.988$8.729$10.998$0.350$0.750$0.500$0.050

表4 组合2输出量

序列号DbDmleαZF(X) 13.26030.114 18.35711.20621−15 328.666 23.11429.7338.96311.34121−15 650.268 33.40229.8328.89511.22921−15 845.115 43.57129.8508.96011.24121−15 406.613 52.95529.6408.90311.32721−14 146.869

5 程序升级与运行

5.1 升级

程序的常规运行需要相当长的时间，但如果进行并行编程运算，则速度会非常快。而实数编码遗传算法可以非常有效地进行并行化处理，这需要在不同处理器上独立运行的不同线程之间设置传递消息接口。

5.2 运行

程序代码可以在任何平台上运行，可执行文件只需要输入名为“input”的文件即可。

基于Unix环境中的相关命令主要有：

$./maker.sh：生成可执行文件“exe”；

$/exe：执行项目程序——输入名为“input”的文件，便会在名为“output”的文件中输出、显示并存储结果；

$/clean.sh：删除所有临时文件并使工作区进入初始状态。

5.3 汇编过程

分布在3个文件中的代码，分别进行单独编译，并生成各自的目标代码文件：

$ g++ -c opti.c

$ g++ -c objective.c

$ g++ -c operators.c

由此生成的目标代码再次进行汇编，以生成可执行文件。

程序从名为“input”的文件中获取输入。此文件接受边界尺寸量，包括五个必备边界尺寸（D、d、B、C、T），以及遗传算法参数。

[1] 张钢,阮娟.基于遗传算法的交叉滚子轴承优化设计[J].轴承,2010 (12):1-7.

[2] 何绍武,邬义杰,周刚.基于改进遗传算法的圆锥滚子轴承优化设计方法研究[J].设计与研究,2006(9):1-7.

[3] 玄光南,程润伟.遗传算法与工程优化[M].北京:清华大学出版社, 2003.

[4] 赵章荣,隋晓梅.基于改进自适应遗传算法的圆锥滚子轴承优化设计[J].机床与液压,2008(8):21-23.

[5] 金晶,苏勇.一种改进的自适应遗传算法[J].计算机工程与应用, 2005(1):64-69.

[6] M.D.Vose. Generalizing the notion of schema in genetic algorithms [J].Artificial Intelligence, 1999(6)22-24.

[7] M.Gen,R.Cheng.Genetic Algorithms and Engineering Design[J]. IEEE New York: Wiley, 2007(5):45-47.

[8] 刘莹.交叉滚子轴承的机理研究[D].上海:上海大学,1985.

[9] 王东峰,叶军.双列圆锥滚子轴承多目标优化设计[J].轴承,2008(8): 8-10.

[10] 徐弘毅.重载滚动轴承的仿真与优化设计[D].北京:清华大学, 2010.

Optimum Design of Tapered Roller Bearing for Vehicle Based on GA with Maximum Dynamic Load

XU Hui, HOU Jianwei, LU Yanqun*

（Hebei University of Engineering, Hebei Handan 057000）

The design method has an important influence on the performance, life and reliability of tapered roller bearings for agricultural machinery, as well as the working performance and economic performance of agricultural machinery using such bearings. The designer's responsibility is to choose the best solution from all possible solutions. Traditionally, the basic requirement of rolling bearings is to meet the maximum dynamic load. Using genetic algorithm (GA) to design tapered roller bearings with maximum dynamic load can satisfy all the boundary conditions and obtain a large multi-dimensional search space. Its purpose is to search and migrate to a more suitable region, that is to say, in this region, the bearing has higher rated dynamic load. This can be achieved by punishing every violation. With the increase of violations, the penalty value increases exponentially.

Vehicle; Tapered roller bearing; maximum load; Genetic algorithm; Optimal design

TB535+.2

A

1671-7988(2021)20-96-05

TB535+.2

A

1671-7988(2021)20-96-05

10.16638/j.cnki.1671-7988.2021.020.023

徐辉（1978—），女，硕士，讲师，就职于河北工程大学机械学院，主攻方向：机械工程。

卢彦群，男，教授，就职于河北工程大学机械与装备学院。

河北省科技厅大智移云应用专项-圆锥滚子轴承双层复合智能化生产线研发（18211832D）；河北省教育厅-面向新工科基于TRIZ的大学生创新能力培养模式研究（2019GJJG250）。