基于一维束流理论的液力变矩器轴向推力分析计算

朱建华，陈黄发，周友，严皓

基于一维束流理论的液力变矩器轴向推力分析计算

朱建华，陈黄发，周友，严皓

（广州汽车集团股份有限公司汽车工程研究院，广东 广州 511434）

液力变矩器是液力式自动变速器的重要零件，起着传递发动机动力给变速器的作用。液力变矩器的泵轮随发动机曲轴旋转，液力变矩器在传递发动机动力的同时，也会对发动机曲轴有轴向推力作用。文章基于一维束流理论，对液力变矩器轴向推力分析计算，计算共有5个步骤，其中第一步的循环流量计算最为重要。从计算结果得知，液力变矩器轴向推力是实际存在的，且对发动机曲轴有压力作用。D230型液力变矩器最大轴向推力3 263.7 N，出现在泵轮转速2 682 r/min、涡轮转速1 776 r/min的工况。

液力变矩器；轴向推力；一维束流理论

前言

液力变矩器是液力式自动变速器的重要零件，起着传递发动机动力给变速器的作用。液力变矩器由泵轮、涡轮、导轮和闭锁离合器构成。液力变矩器在运转过程中，泵轮、涡轮和导轮都会在轴向产生力的作用，现有文献对这些轴向力都有研究，但研究的目的都是基于对液力变矩器内部零件受力分析，用于液力变矩器内部零件设计和强度校核，而并没有系统性的研究液力变矩器对周边零件的作用力。为优化周边零件的设计，就对液力变矩器对周边零件的作用力提出了需求。液力变矩器的泵轮随发动机曲轴旋转，液力变矩器在传递发动机动力的同时，也会对发动机曲轴有轴向推力作用。这个轴向推力对发动机内部零件设计和强度校核都是影响的，如曲轴润滑和止推垫片性能。因此对液力变矩器轴向推力的研究是十分必要的[1-2]。

一维束流理论是传统设计方法的主要理论依据，基于假设叶轮中液流由许多流束组成，流动相对旋转轴对称；基于假设叶轮的叶片数无穷多，厚度无限薄，液流的相对运动轨迹与叶片形状相同，出口液流不受入口流动状况影响，叶轮的出口流动情况，决定下一个叶轮的进口前的流动；基于假设液流与叶片间相互作用，以平均值的设计流线——中间流线表示之，即认为同一过流断面上各点的轴面速度相同。一维束流理论将变矩器内复杂的空间三维流动简化为一维流动[3]。

1 液力变矩器轴向推力产生机理

液力变矩器的横截面示意图。液力变矩器输入端通过螺栓或螺母固定在发动机端驱动盘上，驱动盘与发动机曲轴固定相连，通过泵轮将发动机的机械能量转化为液体能量，而涡轮则从液体中吸收能量并由输出端传递到变速器内部。

基于一维束流理论的液力变矩器的轴向推力主要由三种力组成：静压力对表面积的作用而引起的轴向推力；液体在工作轮弯曲的流道内流动时，液体惯性形成的轴向推力；补偿压力对不平衡面积产生的轴向推力。液力变矩器轴向推力的大小和方向是由三个工作轮（泵轮、涡轮和导轮）的合力组成[1-2]。

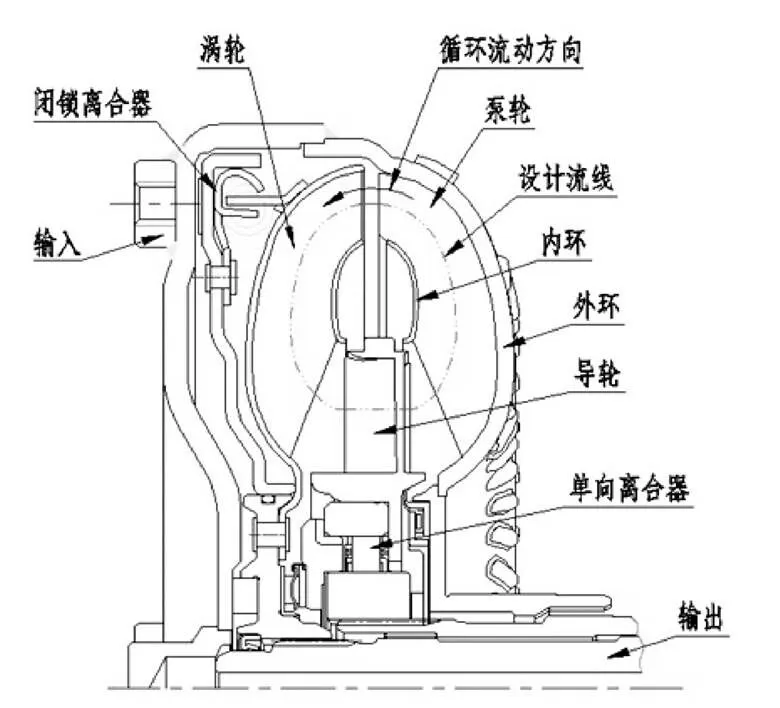
图1 液力变矩器示意图[3]

图2为液力变矩器轴向推力传动路线。泵轮轴向推力方向根据液力变矩器速比大小变化，从朝向发动机方向向背离发动机方向变化；涡轮轴向推力方向始终朝向发动机方向；导轮轴向推力方向始终背离发动机方向。一定速比下的三个工作轮（泵轮、涡轮和导轮）的合力即是液力变矩器轴向推力。液力变矩器轴向推力通过液力变矩器的固定块传递给发动机驱动盘。发动机驱动盘受力后产生形变，即在轴向方向发生一定的位移量，发动机驱动盘有特定的刚度特性，即发动机驱动盘位移与变形力有一一对应关系，通过发动机驱动盘受力后产生的形变，把液力变矩器轴向推力传递到发动机曲轴上，最后作用到发动机内部零件结构上。图3为液力变矩器轴向推力传动流程。液力变矩器轴向推力可以瞬间力，也可以是持续力。

图2 液力变矩器轴向推力传动路线

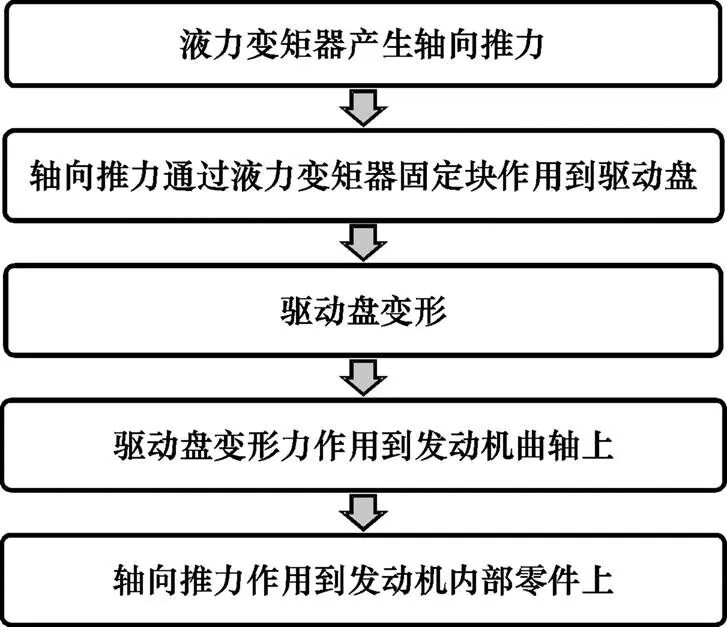
图3 液力变矩器轴向推力传动流程

2 液力变矩器轴向推力计算步骤

为完成基于一维束流理论的液力变矩器的轴向推力计算，首先要完成循环圆设计。过液力变矩器轴心线作截面，在截面上与液体相接的界线形成的形状，称为循环圆。循环圆实际是工作液体在各工作轮内循环流动时，流道的轴面形状，工作液体循环流动是一个封闭的轨迹，因而起名为循环圆。循环圆是由外环、内环、叶轮的入口边和出口边组成的。外环是循环圆的外圈，内环是循环圆的内圈，入口边和出口边是各叶轮内叶片的入口边和出口边的轴面的投影，此外，还应在循环圆上表示出设计流线（或称中间流线）。通过逆向设计可求取外环、内环、叶轮入口边和出口边以及设计流线。按照泵轮、涡轮和导轮的装配尺寸，完成液力变矩器循环圆的结构图设计[3]。

2.1 液力变矩器轴向推力计算简图

图4为液力变矩器轴向推力计算的简图。计算中规定轴向推力方向，向左为正，向右为负。

根据液力变矩器内部流场的分布特性，对于泵轮定义了ch、cd、dg、ba和ai等区域轴向推力；对于涡轮定义了ch、cd、dg、ef和fj等区域轴向推力；对于导轮定义了ba、ai、ef和fj等区域轴向推力；三个工作轮由流体流动惯性力引起的轴向推力AQ。把泵轮与导轮空腔压力平均值定义为点1，把把泵轮与涡轮空腔压力平均值定义为点2，把涡轮与导轮空腔压力平均值定义为点3[4]。

图4 液力变矩器轴向推力计算简图

2.2 液力变矩器轴向推力计算步骤

基于一维束流理论的液力变矩器的轴向推力计算有5个步骤，简要总结如下。

第一步：根据循环圆内工作液体的能量平衡方程，计算三工作轮的循环流量。

式中：系数、和与泵轮转速和涡轮转速有关，即=（ω，ω）；ω为泵轮角速度；ω为涡轮角速度。

解循环流量的二次方程时，有两个根。在两个根中，只有循环流量的正根有研究意义；负根表示循环流量为零以下，这在液力变矩器运转时是不允许出现的，所以不做研究。则正根为：

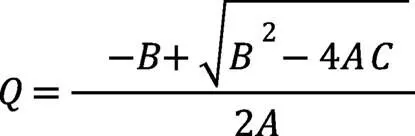
根据上式（2），可以求得液力变矩器在任一泵轮转速和涡轮转速下的循环流量。

第二步：计算三工作轮出口、入口处液流速度。

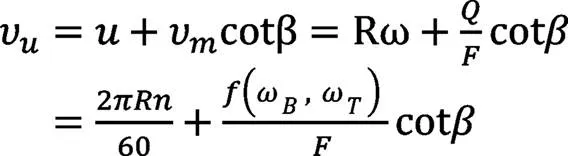
式中：υ为三工作轮出口和入口处液流绝对速度的圆周分速度；为液流圆周速度（相对速度）；υ为液流绝对速度的子午分速度（轴面速度）；为三工作轮入口角、出口角；为三工作轮入口半径、出口半径；为工作轮角速度；为三工作轮入口和出口处流道截面积；为工作轮转速。

第三步：计算三工作轮液体能头和能头损失计算。工作液体在液力变矩器内循环流动时，工作液体与泵轮相互作用吸收能量，与涡轮和导轮相互作用输出能量，同时，工作液体在进入工作轮和在工作轮内流动时，有冲击损失、摩擦损失和扩散损失的能量损耗。

液体流经旋转工作轮后，液体能量变化与液体流动情况变化间关系的欧拉方程：

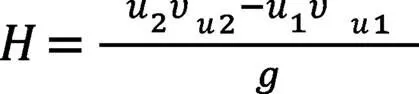
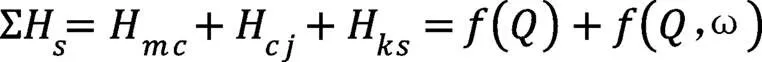
式中：为三工作轮液体能头；ΣH为三工作轮能头损失；H为三工作轮摩擦损失；H为三工作轮冲击损失，H为三工作轮扩散损失。下标1表示入口，下标2表示出口。

第四步：内、外环上对应点的压力计算。

泵轮中间流线上压力：

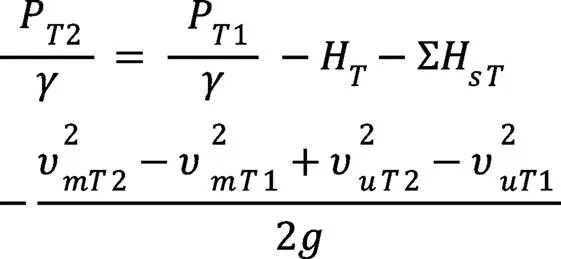
导轮中间流线上压力：

内、外环上对应点的压力：

两轮之间空腔任一点的压力：

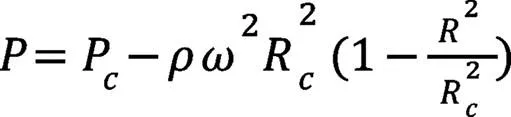
内环内空腔中的压力分布：

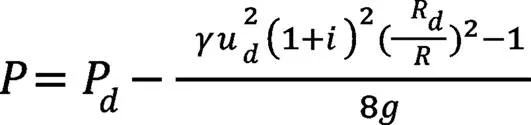
式中：为静压力；为工作液体重度；为工作液体密度。

第五步：三工作轮的轴向推力计算。

泵轮总的轴向推力为：

涡轮总的轴向推力为：

由于篇幅所限，本文无法对六种可能一一给出详细的解释论证，而且本文的重点是对科学公信力生成逻辑中涉及的基本维度要素之间的关系进行剖析检验，故此暂且悬置关联机理的讨论，留待另文阐释。

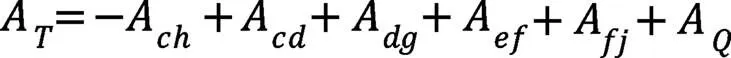
导轮总的轴向推力为：

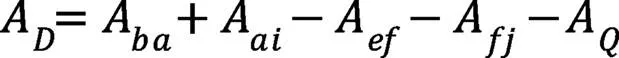
液力变矩器轴向推力：

液力变矩器轴向推力的大小和方向是由三个工作轮（泵轮、涡轮和导轮）的合力组成。计算中规定轴向推力方向，向左为正，向右为负。即朝向发动机的力为正，朝向变速器的力为负。

3 计算循环流量Q

基于一维束流理论的液力变矩器的轴向推力计算有5个步骤，计算三工作轮的循环流量是第一步，也是最关键的一步。如果循环流量计算报错，即在解循环流量的二次方程时，B2−4AC＜0，就不能得到这个工况的循环流量，轴向推力计算也就终止了。

目前有2种计算循环流量的方法，一种是扭矩计算法，如下式（16）；另一种是能量平衡计算法，如下式（17）。

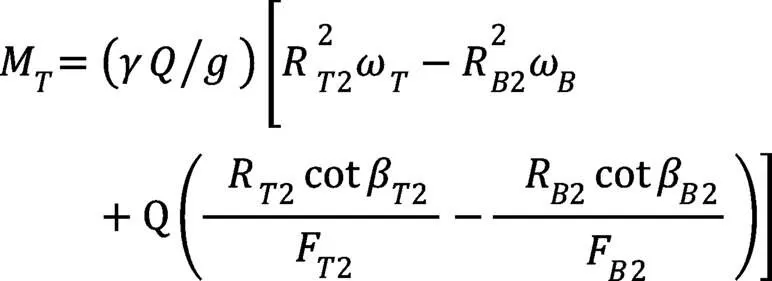
式中：M为涡轮扭矩；R2为涡轮出口半径；R2为泵轮出口半径；β2为涡轮出口角；β2为泵轮出口角；F2为涡轮出口处流道截面积；F2为泵轮出口处流道截面积。式中只有循环流量为未知量，把其他已知量代入即可计算出对应工况的循环流量。

式中：系数a、b、c、d、e和f可由各个方程式计算出；为涡轮和泵轮转速比。

3.1 能量平衡计算法

通过对比分析试验数据，本文采用的能量平衡计算法，即用式（17）来计算出的循环流量更接近实际情况。

液力变矩器的能量平衡式为：

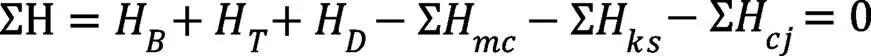
用上式（18）可推导出循环流量方程式（17），式中为涡轮转速和泵轮转速的比值；系数、、、、e和由下列等式表示。

式中：ξ为三工作轮摩擦损失系数；ξ为三工作轮扩散损失系数；ξ为三工作轮冲击损失系数；R1为涡轮入口半径；R1为泵轮入口半径；R1为导轮入口半径；R2为导轮出口半径；β1为涡轮入口角；β1为泵轮入口角；β1为导轮入口角；β2为导轮出口角；F1为涡轮入口处流道截面积；F1为泵轮入口处流道截面积；F1为导轮入口处流道截面积； F2为导轮出口处流道截面积。

3.2 D230型液力变矩器的循环流量Q

在进行计算之前，首先要提取D230型液力变矩器结构参数，三个工作轮（泵轮、涡轮和导轮）的入口角和出口角，三个工作轮（泵轮、涡轮和导轮）的入口处半径和出口处半径，三个工作轮（泵轮、涡轮和导轮）的入口处流道截面积和出口处流道截面积。再代入三个工作轮（泵轮、涡轮和导轮）的冲击损失系数、摩擦损失系数和扩散损失系数，就可计算出在不同速比下的D230型液力变矩器的循环流量，结果如表1、图5所示。

表1 D230型液力变矩器的循环流量

ωT/(r/min)ωB/(r/min)速比i循环流量Q/(m3/s) 02 2050.0000.031 7 1002 2030.0450.032 1 2002 1970.0910.032 2 3002 1880.1370.032 0 4022 3380.1720.034 0 5002 1750.2300.030 9 6002 1780.2750.030 0 6762 3380.2890.031 9 7002 1820.3210.029 0 8002 2060.3630.028 0 9002 2270.4040.026 8 1 0002 2490.4450.025 3 1 1002 2800.4820.023 7 1 2002 3120.5190.021 9 1 3002 3500.5530.019 9 1 4002 4500.5710.019 4 1 6362 6210.6240.015 7 1 7762 6820.6620.011 5 1 9142 7360.7000.006 0 1 9902 7680.7190.002 3

图5 随速比变化的循环流量

根据计算结果，可以看出随着速比的增加，D230型液力变矩器的循环流量逐渐减小，当速比为0.719时，循环流量几乎接近为零。循环流量为零以下，这在液力变矩器运转时是不允许出现的，所以本文对大于速比0.719的工况不作研究。

4 液力变矩器轴向推力计算结果

表2 D230型液力变矩器的轴向推力

ωT/(r/min)ωB/(r/min)速比i轴向推力/N 02 2050.0002 257.49 1002 2030.0452 269.92 2002 1970.0912 274.00 3002 1880.1372 272.02 4022 3380.1722 608.65 5002 1750.2302 278.17 6002 1780.2752 299.92 6762 3380.2892 655.28 7002 1820.3212 322.30 8002 2060.3632 384.50 9002 2270.4042 437.68 1 0002 2490.4452 488.86 1 1002 2800.4822 554.56 1 2002 3120.5192 615.62 1 3002 3500.5532 681.94 1 4002 4500.5712 897.92 1 6362 6210.6243 226.80 1 7762 6820.6623 263.70 1 9142 7360.7003 208.13 1 9902 7680.7193 134.25

在计算出不同速比下的循环流量后，就可对三工作轮出口处和入口处的液流绝对速度的子午分速度（轴面速度）υ、液流圆周速度（相对速度）和液流绝对速度的圆周分速度υ进行计算了；计算完不同速比下的三工作轮出口处和入口处液流速度，再计算出三工作轮液体能头和能头损失；然后再计算出循环圆内环和外环上对应点的压力；就可计算出三工作轮A、A、A、A、A、A、A等各区域的轴向推力和液体流动惯性力引起的轴向推力A，最后把各部分的轴向推力按照力的方向相加或相减，就得到在不同速比下的D230型液力变矩器的轴向推力，结果如表2、图6所示。

图6 随速比变化的轴向推力

从计算结果可以看出，液力变矩器轴向推力大小随速比升高而增加，轴向推力大小从失速的2 257.49 N上升到速比0.662的3 263.70 N；液力变矩器轴向推力的方向是从变速器到发动机方向，即对发动机的驱动盘产生压力作用。

5 结论

从计算结果得知，液力变矩器轴向推力是实际存在的，且对发动机曲轴有压力作用。D230型液力变矩器最大轴向推力3 263.7 N，出现在泵轮转速2 682 r/min、涡轮转速1 776 r/min的工况。这个工况在整车运行中是有可能出现的，所以在发动机设计和耐久试验工况设计时必须考虑这个作用在曲轴上的轴向推力。

一维束流理论对液力变矩器内部流场的简化设计和分析，决定了通过一维束流理论计算出的轴向推力与实际的轴向推力有一定的偏差。为更精确掌握各工况下的液力变矩器轴向推力，如加速换档、弹射起步和爬坡等工况的液力变矩器轴向推力，为发动机设计和验证提供更可靠的数据，就需要通过整车试验来得到实际的液力变矩器轴向推力。

[1] 朱经昌.液力变矩器的设计与计算[M].北京:国防工业出版社, 1991:184-190.

[2] 朱经昌,魏宸官,郑慕侨,等.车辆液力传动(上、下)[M].北京:国防工业出版社,1982:371-377.

[3] 朱建华.液力变矩器理论设计方法的研究[D].重庆:重庆大学, 2008.12-23.

[4] 侯天强,刘光隆,吕浩,等.液力变矩器轴向力研究[J].机械工程师, 2013(11):42-45.

Analysis and Calculation of Axial Thrust of Torque Converter Based on One-dimensional Theory

ZHU Jianhua, CHEN Huangfa, ZHOU You, YAN Hao

( GAC R&D Center, Guangdong Guangzhou 511434 )

Torque converter is an important part of hydraulic automatic transmission, which plays the role of transmitting engine power to transmission. Pump of torque converter rotates with crankshaft of engine. While torque converter transmits engine power, it also exerts an axial thrust on the crankshaft of engine. Based on the one-dimensional theory, this paper analyzes and calculates the axial thrust of torque converter, there are 5 steps in the calculation, and circulation flow calculation in the first step is the most important. From calculation results, it is known that axial thrust of torque converter actually exists and has a pressure effect on engine crankshaft. Maximum axial thrust of D230 torque converter is 3263.7 N, which appears in working conditions of pump speed of 2682 r/min and turbine speed of 1776 r/min.

Torque converter;Axial thrust;One-dimensional theory

U463.212

A

1671-7988(2021)20-65-06

U463.212

A

1671-7988(2021)20-65-06

10.16638/j.cnki.1671-7988.2021.020.016

朱建华，硕士，高级工程师，就职于广州汽车集团股份有限公司汽车工程研究院，主要从事整车项目变速器系统应用匹配开发。